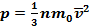Идеальный газ – это модель реального газа. За идеальный газ принимают газ в сосуде, когда молекула, пролетая от стенки до стенки сосуда не испытывает столкновения с другими молекулами. Точнее, Идеальный газ – это газ, взаимодействие между молекулами которого пренебрежимо мало ⇒ Eк >> Eр .
Основное уравнение МКТ связывает макроскопические параметры (давление p, объём V, температура T, масса m) газовой системы с микроскопическими параметрами (масса молекулы , средняя скорость их движения):
, где n— концентрация, 1/м 3 ; m — масса молекулы, кг; 
Уравнение состояния идеального газа — формула, устанавливающая зависимость между давлением , объёмом и абсолютной температурой идеального газа, характеризующее состояние данной системы газа. 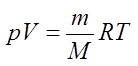
Часто необходимо исследовать ситуацию, когда меняется состояние газа при его неизменном количестве (m=const) и в отсутствие химических реакций (M=const). Это означает, что количество вещества ν=const. Тогда:
Для постоянной массы идеального газа отношение произведения давления на объем к абсолютной температуре в данном состоянии есть величина постоянная: 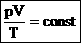
Термодинамический процесс (или просто процесс) — это изменение состояния газа с течением времени. В ходе термодинамического процесса меняются значения макроскопических параметров — давления, объёма и температуры. Особый интерес представляют изопроцессы — термодинамические процессы, в которых значение одного из макроскопических параметров остаётся неизменным. Поочерёдно фиксируя каждый из трёх параметров, мы получим три вида изопроцессов.
Последнее уравнение называют объединённым газовым законом. Из него получаются законы Бойля — Мариотта, Шарля и Гей-Люссака. Эти законы называют законами для изопроцессов:
Изопроцессы – это процессы, которые совершаются при одинаковом параметре или Т-температуре, или V-объеме, или р-давлении.

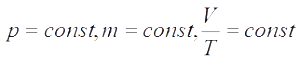
Изохорный п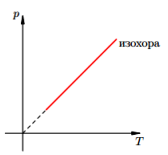
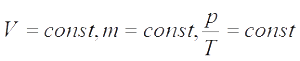
Вывели газовые законы из уравнения Менделеева — Клапейрона. Но исторически всё было наоборот: газовые законы были установлены экспериментально, и намного раньше. Уравнение состояния появилось впоследствии как их обобщение.
Видео:Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Уравнение клайперона менделеева для всех изопроцессов
Уравнение Менделеева-Клапейрона — уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем Vm и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:
pV = RT , где R — универсальная газовая постоянная,
R = 8,31 Дж/(моль . К)
Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа. Для произвольной массы газа М, молярная масса которого m: pV = (М/m) . RT. или pV = NАkT,
где NА — число Авогадро, k — постоянная Больцмана.
С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров — давление, объем или температура — остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.
Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.
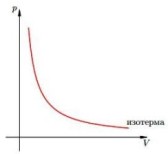
Изотермический процесс — процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля — Мариотта.
Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой — термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P1V1=P2V2=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.
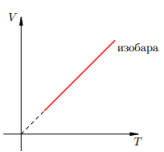
Изобарный процесс — процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.
Изохорный процесс — процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.
Итак, из закона pV = (М/m) . RT выводятся следующие законы:
p = const => V/T = const — закон Гей — Люссака .
V= const => p/T = const — закон Шарля
Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление — это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.
Некоторых, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро NA = 6,02·10 23 ? Значение числа Авогадро было экспериментально установлено только в конце XIX – начале XX века. Опишем один из таких экспериментов.
В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10 10 альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10 -4 атм (при температуре 27 о С). Изменением массы радия за год можно пренебречь. Итак, чему равна NA?
Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:
N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.
Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/NA. Отсюда:
NA = NRT = 5,83 . 10 17 . 0,0821 . 300 = 6,02 . 10 23
PV 7,95 . 10 -4 . 3 . 10 -2
В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Лекция «Уравнение Менделеева-Клапейрона. Газовые законы. Изопроцессы.»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
Уравнение Менделеева-Клапейрона. Газовые законы. Изопроцессы
Молекулы в идеальном газе движутся хаотически. Движение одной молекулы характеризуют микроскопические параметры (масса молекулы, ее скорость, импульс, кинетическая энергия). Свойства газа как целого описываются с помощью макроскопических параметров (масса газа, давление, объем, температура). Молекулярно-кинетическая теория устанавливает взаимосвязь между микроскопическими и макроскопическими параметрами.
Число молекул в идеальном газе столь велико, что закономерности их поведения можно выяснить только с помощью статистического метода. Равномерное распределение в пространстве молекул идеального газа является наиболее вероятным состоянием газа, т. е. наиболее часто встречающимся.
Распределение молекул идеального газа по скоростям при определенной температуре является статистической закономерностью.
Наиболее вероятная скорость молекул — скорость, которой обладает максимальное число молекул. Стационарное равновесное состояние газа — состояние, в котором число молекул в заданном интервале скоростей остается постоянным.
Температура тела — мера средней кинетической энергии поступательного движения его молекул:
где черта сверху — знак усреднения по скоростям, k = 1,38 • 10 -23 Дж/К — постоянная Больцмана.
Единица термодинамической температуры — кельвин (К).
При абсолютном нуле температуры средняя кинетическая энергия молекул равна нулю.
Средняя квадратичная (тепловая) скорость молекул газа
где М — молярная масса, R = 8,31 Дж/(К • моль) — молярная газовая постоянная.
Давление газа — следствие ударов движущихся молекул:
где n — концентрация молекул (число молекул в единице объема), E k — средняя кинетическая энергия молекулы.
Давление газа пропорционально его температуре :
Постоянная Лошмидта — концентрация идеального газа при нормальных условиях (атмосферное давление р= 1,01 • 10 5 Па и температура Т = 273 К):
Уравнение Клапейрона—Менделеева — уравнение состояния идеального газа, связывающее три макроскопических параметра (давление, объем, температуру) данной массы газа.
Изопроцесс — процесс, при котором один из макроскопических параметров состояния данной массы газа остается постоянным. Изотермический процесс — процесс изменения состояния определенной массы газа при постоянной температуре.
Закон Бойля—Мариотта : для газа данной массы при постоянной температуре:
где р 1 , р 2 , V 1 , V 2 — давление и объем газа в начальном и конечном состояниях
Изотерма — график изменения макроскопических параметров газа при изотермическом процессе. Изобарный процесс — процесс изменения состояния определенной массы газа при постоянном давлении.
Закон Гей-Люссака : для газа данной массы при постоянном давлении
где V 1 , V 2 , T 1 , Т 2 — объем и температура газа в начальном и конечном состояниях.
Изобара — график изменения макроскопических параметров газа при изобарном процессе.
Изохорный процесс — процесс изменения состояния определенной массы газа при постоянном объеме. Закон Шарля: для газа данной массы при постоянном объеме
где p 1 , р 2 , T 1 , Т 2 — давление и температура газа в начальном и конечном состояниях.
Изохора — график изменения макроскопических параметров газа при изохорном процессе.
🔍 Видео
Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Уравнение состояния идеального газа. 10 класс.Скачать

Решение графических задач на тему Газовые законыСкачать

Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

Уравнение Менделеева-Клапейрона и 4 изопроцесса для состояния идеального газа (графики и смысл).Скачать

Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

62. Уравнение Клапейрона-МенделееваСкачать

Изопроцессы в газах, уравнение Менделеева -КлапейронаСкачать

#5 Изопроцессы. Уравнение Мендлеева-Клапейрона.Скачать

Газовые законы. Изопроцессы в физикеСкачать

Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать

Урок 158. Задачи на газовые законы - 1Скачать

Уравнение Менделеева - Клапейрона за 10 минут | Физика с Никитой АрхиповымСкачать