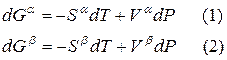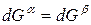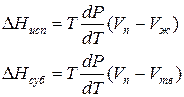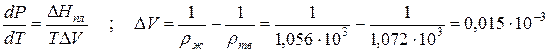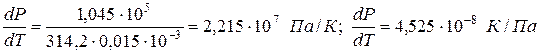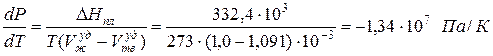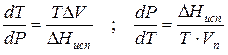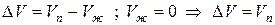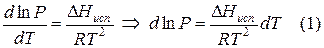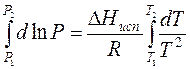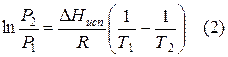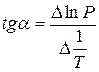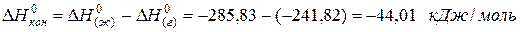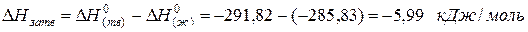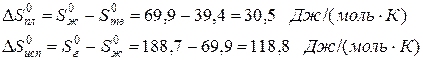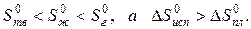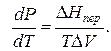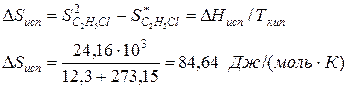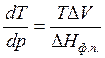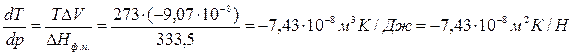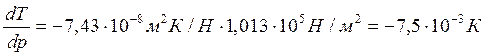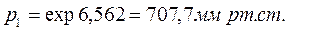ТЕПЛОВЫЕ ЭФФЕКТЫ ФАЗОВЫХ ПЕРЕХОДОВ.
УРАВНЕНИЕ КЛАПЕЙРОНА – КЛАУЗИУСА.
Переход компонента из одной фазы в другую сопровождается выделением или поглощением теплоты, которую можно определить количественно на основе фундаментального уравнения термодинамики:
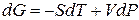
ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.
Для любого равновесного перехода вещества из одной фазы α в другую фазу β, применяя уравнение (*) к каждой из фаз, можно написать
Индексы α и β отражают принадлежность параметров к соответствующей фазе. В равновесных условиях между фазами α и β изменение энергии Гиббса отсутствует, т.е.
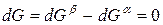
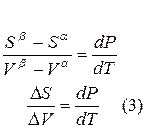
Для равновесного обратимого процесса согласно уравнениям 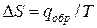
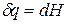
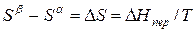
а уравнение (3) примет вид
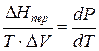
где ∆Hпер – теплота фазового перехода.
Тепловой эффект, сопровождающий фазовый переход, определяется следующим образом:
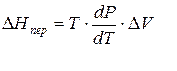
Клапейрона–Клаузиуса
где ∆V – изменение объема в результате фазового перехода; dP/dT – изменение давления в зависимости от температуры при сохранении равновесия между двумя фазами.
Уравнение Клапейрона–Клаузиуса связывает тепловой эффект процесса с изменением давления насыщенного пара, температурой и изменением объема в процессе фазового перехода.
Для процессов испарения ж→п и сублимации тв→п уравнение Клапейрона–Клаузиуса можно представить следующим образом:
где ∆Hисп , ∆Hсуб – теплоты испарения и сублимации; Vп, Vж, Vтв – мольные объемы пара, жидкости и твердого тела соответственно.
В процессе испарения и сублимации наблюдается значительное изменение удельного объема ∆V и существенное изменение величины dP/dT. При плавлении, напротив, изменение ∆V невелико, и величина dP/dT незначительна.
Пример 1. Проведем расчет по уравнению Клапейрона–Клаузиуса температуры плавления фенола Тпл. Плотность твердого фенола ρтв при атмосферном давлении составляет 1,072∙10 3 кг/м 3 , а жидкого ρж = 1,056∙10 3 кг/м 3 ; теплота плавления ∆Hпл = 1,045∙10 5 Дж/кг; температура замерзания 314,2 К. Определим dP/dT и температуру плавления при Р = 5,065∙10 7 Па:
Прирост температуры плавления при повышении давления на 1 атм ( 1,013∙10 5 Па) составляет 4,525∙10 -8 град/Па. При увеличении давления до 5,065∙10 7 Па температура плавления увеличивается на ∆T = (dT/dP)∆P = 4,525∙10 -8 ∙ 5,065∙10 7 = 2,29 К, т.е. составит Тпл = 314,2+2,29 = 316,49 К.
Следует иметь в виду, что в процессе плавления у большинства веществ Vж > Vтв , тогда ∆V>0 и при повышении давления Р↑ температура плавления повышается Т↑.
Однако, такие вещества как вода (Н2О), висмут (Bi), имеют объем твердой фазы Vтв больше, чем объем жидкой фазы Vж уд = 10 -3 м 3 /кг и Vтв уд = 1,091·10 -3 м 3 /кг; теплота плавления ∆Hпл = 332,4 кДж/кг:
Это значение показывает, что для понижения температуры таяния льда на один градус Кельвина необходимо увеличить давление на 1,34∙10 7 Па, т.е. примерно на 134 атмосферы, что нереально, поскольку такое давление лед не выдерживает – трескается.
Таяние льда происходит в основном в результате трения и превращения работы в теплоту при скольжении конька по льду, а не за счет повышения давления на лед.
Уравнение для процесса испарения 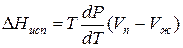
Пар подчиняется законам идеального газа: PV=RT 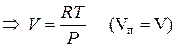
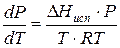
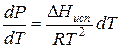
Проведем интегрирование уравнения (1) в пределах от Т1 до Т2 и соответственно от Р1 до Р2 при условии, что в области невысоких давлений пара ∆Нисп ≈ const; в результате интегрирования получим:
∆Нисп / R = const, выносим за знак интеграла
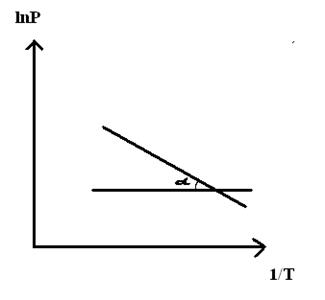
При помощи уравнения (2) можно графически определить значения теплоты испарения, если известны давления Р1 и Р2 и соответствующие им температуры испарения Т1 и Т2 . Для этого необходимо отложить на оси абсцисс значения обратной температуры, а на оси ординат – lnP.
Зависимость lnP от 1/Т будет линейной, а тангенс угла наклона этой прямой равен 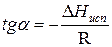
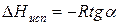
Расчетные значения ∆Нисп получаются с достаточной для практики точностью, не уступающей точности непосредственного измерения. Возможно использование уравнения (2) для обратного расчета, когда по значению ∆Нисп определяют изменение давления при изменении температуры в процессе испарения.
Теплоту фазовых переходов можно определить и по величине стандартной энтальпии образования, в зависимости от фазового состояния продуктов реакции.
Пример. Лучше всего это показать на примере теплоты образования воды из газообразных кислорода и водорода, которая составляет
для водяного пара ∆Н(г) 0 = -241,82 кДж/моль; для воды в жидком состоянии ∆Н(ж) 0 = -285,83 кДж/моль; для льда ∆Н(тв) 0 = -291,82 кДж/моль. Теплота конденсации воды равна:
а теплота превращения воды в лед:
Как видно, тепловой эффект фазовых переходов значительно меньше теплоты образования веществ.
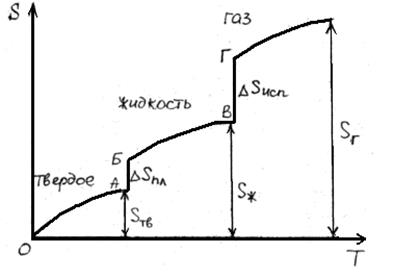
В результате фазовых переходов происходит изменение энтропии. Такие изменения в зависимости от температуры представим на рисунке.
Как известно, энтропия идеального кристалла при абсолютном нуле равна нулю. С ростом температуры атомы (ионы) флуктуировать относительно равновесного положения, число возможных способов их размещения растет, и энтропия увеличивается (ΔS>0). При достижении температуры плавления (точка А на рисунке) кристаллическая решетка разрушается скачкообразно (отрезок АБ), увеличивается термодинамическая вероятность системы W, а в соответствии с формулой S=k∙lnW (где k – постоянная Больцмана) энтропия при переходе от твердого в жидкое состояние растет. Более значительный скачок энтропии имеет место при переходе из жидкого состояния в газообразное (отрезок ВГ), когда ближний порядок расположения частиц друг относительно друга нарушается, и движение частиц становится хаотичным.
Пример. Оценим скачок энтропии на примере фазовых переходов воды:
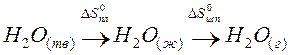
когда известны стандартные абсолютные значения энтропии Sтв 0 =39,4; Sж 0 =69,9; Sг 0 =188,7 Дж/(моль·К).
В соответствии с рисунком для воды
По известной энтальпии фазового перехода можно рассчитать изменение энтропии в соответствии с формулой
Пример.Вычислим изменение энтропии в процессе парообразования 1 моля этилхлорида при 12,3 0 С, когда теплота испарения ∆Нисп =24,16 кДж/моль.
Молекулярная масса 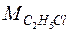
В заключение отмечу, что мы рассматривали лишь фазовые переходы I рода. При фазовых переходах I рода свойства веществ, выражаемые, например, через химический потенциал, первыми производными одной из характеристических функций, изменяются скачком при непрерывном изменении соответствующих параметров: температуры, давления, объема и энтропии. При этом выделяется или поглощается теплота перехода ∆Нпер в соответствии с уравнением Клапейрона–Клаузиуса.
Кроме них, однако, существуют фазовые переходы II рода. Они не сопровождаются выделением или поглощением теплоты, для них уравнение Клапейрона–Клаузиуса теряет смысл. Эти переходы характеризуют изменения в системе, которые не определяются объемом и запасом энергии. В этом случае первые производные одной из характеристических функций непрерывны, а вторые производные (например, теплоемкость) изменяются скачком. К фазовым переходам II рода относятся переходы парамагнетика в ферромагнетик, диэлектрика в сегнетоэлектрик, а также процессы возникновения сверхтекучести, сверхпроводимости и др.
В настоящее время насчитывается около 400 твердых минералов, для которых наблюдаются фазовые переходы II рода: рутил, анатаз, алмаз и особенно кварц, который имеет семь модификаций, причем наряду с фазовыми переходами I рода наблюдаются фазовые переходы II рода. Так, при 573 0 С и переходе модификации кварца β 
| | | следующая лекция ==> | |
| ДИАГРАММА СОСТОЯНИЯ СЕРЫ. | | | ХАРАКТЕРИСТИКА И СВОЙСТВА РАСТВОРОВ. |
Дата добавления: 2016-02-02 ; просмотров: 3127 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Видео:Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Уравнение Клаузиуса – Клайперона и его анализ.
Представьте себе чашку со льдом и водой. Чашка находится в комнате с температурой 0 о С. Лед и вода находятся в равновесии друг с другом, и их соотношение остается неизменным, хотя в отдельных микроскопических участках мы можем обнаружить переход воды из жидкого агрегатного состояния в твердое и наоборот. Эта картинка соответствует равновесной системе, в которой происходит обратимый процесс (плавление – кристаллизация) и нет химической реакции ( — δWm полезн = 0) .
В условиях равновесия: μж = μлед.
В соответствии с dG ≤ — δWm полезн – SdT + VdP. Для одного моля можно записать:
с учетом μж = μлед, уравнивая и вынося подобные члены получаем:
Так как тут процесс плавление – кристаллизация проходит при постоянном давлении то ∆s = hпл/T, hпл — теплота плавления одного моля вещества. Подставляя в (11.2) получаем уравнение Клаузиуса — Клайперона:
Уравнению (11.3) соответствует кривая 1 (кривая зависимости давления плавления от температуры плавления (так не говорят) или кривая зависимости температуры плавления от давления (так говорят)). Процесс плавления протекает с поглощением теплоты (эндотермический, положительный процесс) поэтому hпл > 0. (Для процесса кристаллизации наоборот). Температура положительная величина. Изменение объема может быть как положительным, так и отрицательным. В зависимости от этого кривая наклоняется в лево или в право. Аналогично в зависимости от к в уравнении у = кх.
Для процессов испарения и возгонки уравнение (11.3) удобнее представить в виде:
dlnP/dT = ∆H/T 2 R. (11.4)
Здесь все переменные положительны, поэтому dlnP/dT положительно и кривые возгонки (3) и испарения (2) наклонены вправо.

12. Фазовое равновесие в однокомпонентной системе. Диаграмма состояний
Рассмотрим и проанализируем диаграмму состояния воды (рис.1.4). Поскольку вода – единственное присутствующее в системе вещество, число независимых компонентов К = 1. В системе возможны три фазовых равновесия: между жидкостью и газом (линия ОА – зависимость давления насыщенного пара воды от температуры), твердым телом и газом (линия ОВ – зависимость давления насыщенного пара надо льдом от температуры), твердым телом и жидкостью (линия ОС – зависимость температуры плавления льда от давления). Три кривые имеют точку пересечения О, называемую тройной точкой воды; тройная точка отвечает равновесию между тремя фазами.
Рис. 1.4. Диаграмма состояния воды
В тройной точке система трехфазна и число степеней свободы равно нулю; три фазы могут находиться в равновесии лишь при строго определенных значениях температуры и давления (для воды тройная точка отвечает состоянию с Р = 6.1 кПа и Т = 273.16 К).
Кривая ОВ теоретически продолжается до абсолютного нуля, а кривая давления насыщенного пара над жидкостью ОА заканчивается в критической точке воды (Tкр = 607.46 К, Ркр = 19.5 МПа); выше критической температуры газ и жидкость не могут существовать как отдельные фазы. Кривая ОС в верхней части (при высоких давлениях) изменяет свой наклон (появляются новые кристаллические фазы, плотность которых, в отличие от обычного льда, выше, чем у воды).
Внутри каждой из областей диаграммы (АОВ, ВОС, АОС) система однофазна; число степеней свободы системы равно двум (система дивариантна), т.е. можно одновременно изменять и температуру, и давление, не вызывая изменения числа фаз в системе:
На каждой из линий число фаз в системе равно двум и, согласно правилу фаз, система моновариантна, т.е. для каждого значения температуры имеется только одно значение давления, при котором система двухфазна:
Влияние давления на температуру фазового перехода описывает уравнение Клаузиуса – Клапейрона:

Здесь ΔVфп = V2 – V1 есть изменение молярного объема вещества при фазовом переходе (причем V2 относится к состоянию, переход в которое сопровождается поглощением теплоты). Уравнение Клаузиуса – Клапейрона позволяет объяснить наклон кривых равновесия на диаграмме состояния однокомпонентной системы. Для переходов «жидкость – пар» и «твердое вещество – пар» ΔV всегда больше нуля; поэтому кривые на диаграмме состояния, отвечающие этим равновесиям, всегда наклонены вправо (повышение температуры всегда увеличивает давление насыщенного пара). Поскольку молярный объем газа много больше молярного объема того же вещества в жидком или твердом агрегатном состояниях (Vг >> Vж, Vг >> Vт), уравнение (I.109) для частных случаев испарения и возгонки примет следующий вид:

Для многих веществ скрытая теплота парообразования или возгонки постоянна в большом интервале температур; в этом случае уравнение (I.110) можно проинтегрировать:

Кривая равновесия «твердое вещество – жидкость» на диаграммах состояния воды и висмута наклонена влево, а на диаграммах состояния остальных веществ – вправо. Это связано с тем, что плотность воды больше, чем плотность льда (и плотность жидкого висмута больше его плотности в твердом состоянии), т.е. плавление сопровождается уменьшением объема (ΔV 0 и, согласно уравнению Клаузиуса – Клапейрона, увеличение давления приводит к повышению температуры плавления.
Условием равновесия в однокомпонентной системе является равенство химических потенциалов и изменений химических потенциалов для всех фаз.
Закон Гиббса. Пусть есть система из Ф фаз в которых распределены К компонентов. На систему оказывают свое воздействие N физических факторов. Для описания этой системы нам надо указать состав каждой из фаз и величины влияющих физических факторов. То есть Ф(К – 1) + N переменных. (К – 1) – потому что если фаза состоит из 3 компонентов, то нам надо задать концентрации двух. В условиях равновесия в системе химические потенциалы у каждого компонента во всех фазах между собой будут равны. И через химические потенциалы будут между собой связаны составы фаз. Это уменьшит число переменных на (Ф – 1)К.
С = Ф(К – 1) + N — (Ф – 1)К
Выражение (12.2) носит название правило фаз Гиббса.
С – число переменных, которое необходимо знать, чтобы полностью охарактеризовать систему в любой точке на диаграмме. С другой стороны число степеней свободы, переменные которые мы можем свободно менять в системе в определенных пределах без изменения числа фаз.
Вернемся к рисунку 1. В тройной точке в равновесии находятся 3 фазы, N = 2 (давление и температура), компонент один, поэтому число степеней свободы 0. Это значит что мы ни чего не можем изменить. Если мы будем подводить тепло, то оно будет расходоваться на плавления льда. И пока лед не растает система будет неизменной. Когда лед растает мы перейдем на линию 2 – испарения. Число фаз 2. число степеней свободы 1. это значит мы можем произвольно менять или Р или Т. Что-то одно, вторая переменная изменится автоматически. Меняя или Р или Т мы будем двигаться по кривой испарения. Если вся жидкость испарится то мы окажемся в области пара. Фаза одна число степеней свободы 2. То есть можно одновременно менять и Р и Т.
Видео:Физическая химия # 2. Вывод уравнения Клаузиуса-КлапейронаСкачать

Уравнение Клапейрона — Клаузиуса
Процессы фазового перехода сопровождаются выделением или поглощением теплоты. Зависимость между теплотой фазового перехода и внешними условиями выражается уравнением Клапейрона – Клаузиуса:
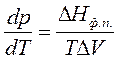
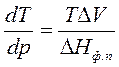
где ΔНф.п. – теплота фазового перехода; ΔV – изменение молярного объема при переходе из одной фазы в другую, 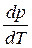
В процессе плавления (кривая ОВ, рис.3.1), объем образующейся жидкой фазы больше объема твердой фазы ( 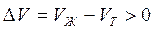
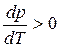
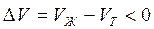
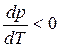
В процессе испарения и возгонки (кривые ОС и ОА на рис. 3.1 и рис. 3.2) производная 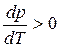
Точка О называется тройной точкой, так как в ней могут находиться в равновесии одновременно три фазы: твердая, жидкая и газообразная. Число степеней свободы в тройной точке равно: С = 3 ─ Ф = 3 ─ 3= 0. Это значит, что произвольно нельзя изменять ни один из параметров, иначе состояние равновесия в системе изменится.
Давление, которое молекулы пара, находящегося в равновесии с жидкой фазой, оказывают на стенки сосуда и на поверхность жидкости, называется давлением насыщенного пара (для краткости давление пара жидкости).
Согласно правилу фаз система с одним компонентом и двумя сосуществующими фазами имеет только одну степень свободы С = 3 ─ Ф = 3 ─ 2 = 1. Следовательно, в процессе испарения можно произвольно изменять один из параметров (либо температуру, либо давление), и при этом не изменится число и природа фаз.
Давление пара над поверхностью стабильного химического вещества (жидкости или твердого тела) определяется только температурой и не зависит от количества взятого вещества, от количества пара и от наличия и концентрации воздуха или другого газа, инертного по отношению к другому пару.
Пример 3.1. Как изменится температура плавления льда при повышении давления на 1 атм, если известно, что при 0°С теплота плавления льда равна 333,5 Дж/г, а удельные объемы воды и льда соответственно равны 1,0001·10 -6 м 3 /г и 1,0908·10 -6 м 3 /г?
Решение:
Плавление льда представляет собой фазовый переход:
твердое вещество →жидкость.
Запишем уравнение Клапейрона – Клаузиуса для процесса плавления в следующем виде:
Т=273К, ΔV=Vж – Vтв = 1,0001·10 -6 – 1,0908·10 -6 = –9,07·10 -8 м 3 /г;
При повышении давления на 1 атм температура плавления льда снизится на 0,0075 градуса.
Применение уравнения Клапейрона – Клаузиуса
К процессам испарения и возгонки
Для процессов испарения и возгонки уравнение Клапейрона-Клаузиуса удобнее представить в другой форме. Так как мольный объем вещества в газообразном состоянии значительно больше мольного объема вещества в жидком состоянии (например, объем 1 моль идеального газа составляет 22,4 л, объем 1 моль жидкой воды равен 18 мл), то изменение объема в процессе испарения (возгонки) ΔV можно считать практически равным объему пара и заменить ΔV ≈ Vп. С учетом того, что для 1 моль вещества V = RT/p, получаем уравнение Клапейрона – Клаузиуса для процессов испарения и возгонки:
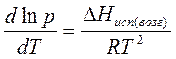
где 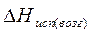
Расчет теплоты испарения и возгонки по уравнению
Клапейрона – Клаузиуса
Теплота испарения (теплота возгонки) является постоянной величиной, то есть не зависит от температуры. Величину теплоты испарения (возгонки) рассчитывают графическим и аналитическим способами.
Графический способ:
Теплоту испарения (возгонки) графическим способом можно найти, если проинтегрировать (неопределенный интеграл) уравнение Клапейрона – Клаузиуса:
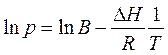
где ln В – постоянная интегрирования, зависящая от размерности, в которой выражено давление (Па, мм рт.ст., атм.).
Полученное уравнение представляет собой уравнение прямой линии, тангенс угла наклона которой равен отношению теплоты испарения (возгонки) к универсальной газовой постоянной.
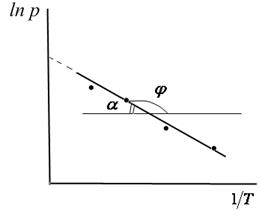 Рис.3.3. Линейная зависимость ln p от обратной температуры Рис.3.3. Линейная зависимость ln p от обратной температуры | 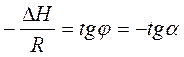 ; ; 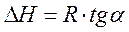 (3.8) (3.8) |
Аналитический способ:
После интегрирования уравнения (3.6) в пределах от р1 до р2 и от Т1 до Т2 получаем:
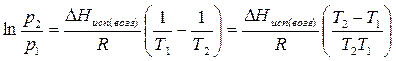
Полученное уравнение позволяет, зная давления пара вещества при двух разных температурах, рассчитать теплоту испарения (возгонки):
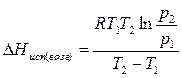
Пример 3.2. Определите давление, при котором вода закипит при 98°С.
Решение:
Кипение воды представляет собой фазовый переход:
Из справочных данных известно, что при 100°С давление насыщенного водяного пара равно 760 мм рт.ст, а удельная теплота испарения составляет 40644 Дж/моль.
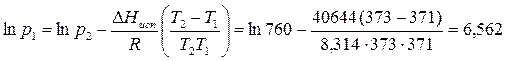
При 98°С вода закипит при давлении, равном 707,7 мм рт.ст.
Пример 3.3. Давление пара бензола при 20°С и 30°С соответственно равно 100·10 2 Па и 157·10 2 Па. Рассчитайте молярную теплоту испарения.
🎦 Видео
Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Плавление и кристаллизация твердых тел, температура плавления, удельная теплота плавления. 8 класс.Скачать

Основы молекулярной физики | уравнение КлапейронаСкачать

Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать

Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

Урок 120 (осн). Задачи на теплоту плавленияСкачать

Урок 119 (осн). Плавление и кристаллизация. Удельная теплота плавленияСкачать

Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

Плавление и отвердевание кристаллических телСкачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Урок 2.Уравнение Менделеева-Клапейрона. Решение задач. База. ЕГЭСкачать

Уравнение состояния идеального газа. 10 класс.Скачать

Фазовые диаграммы. Тройная точка. Критическое состояние вещества. 10 класс.Скачать

Удельная теплота плавления: тема за 5 МИНУТСкачать

Уравнение КЛАПЕЙРОНА-КЛАЗИУСА | МОЛЕКУЛЯРКА (лекция) - КАРАВАЕВ В. А. ФизФак МГУСкачать

Л7 - Теплообмен при фазовых переходах.Скачать