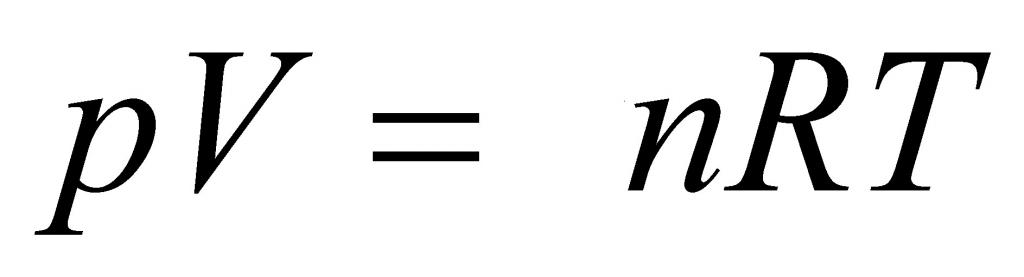Уравнение клапейрона менделеева когда используется

Рассмотрение свойств газов в физике в первом приближении основывается на концепции идеального газа. В данной статье подробно изучим эту концепцию и приведем уравнение, которое описывает численно термодинамические свойства упомянутой текучей субстанции. Это уравнение называется законом Клапейрона-Менделеева.

Видео:Задачи на уравнение Менделеева-Клапейрона. Ч.1. Краткая теория + решение задачиСкачать

Концепция идеального газа

В школьном курсе физики газовое агрегатное состояние вещества характеризуется произвольным перемещением с различными скоростями всех составляющих его атомов и молекул. Эти частицы считаются в первом приближении абсолютно упругими материальными точками. Они имеют массу, но не размеры. Весь характер их взаимодействия друг с другом заключается в абсолютно упругих столкновениях, в результате которых сохраняется количество движения и энергия. Все перечисленные свойства частиц и их приближения образуют концепцию идеального газа.

Любой реальный газ, будь то гелий, кислород или воздух, можно с высокой точностью считать идеальным, если его давление составляет порядка одной атмосферы и ниже, а температура соответствует комнатной или выше. Если эти условия не выполняются, то газ считается реальным, и для его описания следует использовать уравнение Ван-дер-Ваальса, а не закон Клапейрона-Менделеева, о котором пойдет речь далее в статье.

Видео:Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Предпосылки возникновения уравнения состояния идеального газа

Под уравнением состояния газа идеального принято понимать математическую формулировку газового закона Менделеева-Клапейрона. Как и любое открытие в физике, это уравнение не появилось из неоткуда, а имело вполне определенные исторические предпосылки.

В 60-70-е годы XVII века англичанин Роберт Бойль и француз Эдм Мариотт независимо друг от друга в результате многих проведенных экспериментов с различными газами установили, что произведение объема на давление для закрытой системы с газом остается постоянным для любых процессов, в результате которых температура не изменяется. В настоящее время этот газовый закон носит фамилии названных ученых.

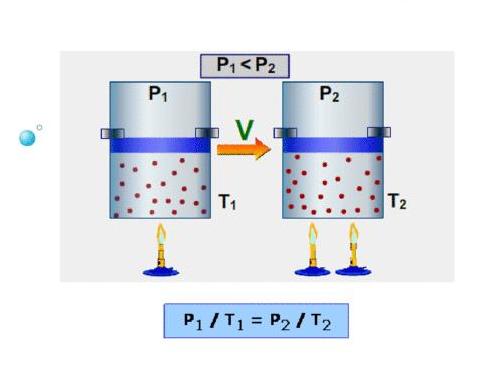
Спустя почти 1,5 века, в конце XVIII — начале XIX веков французы Шарль и Гей Люссак открывают еще два экспериментальных закона в поведении идеальных газов. Они устанавливают прямо пропорциональную зависимость между давлением и температурой при постоянном объеме и между объемом и температурой при постоянном давлении.

Наконец, в 1834 году Эмиль Клапейрон вывел, анализируя открытые предыдущими учеными газовые законы, уравнение Клапейрона. Менделеева фамилия появилась в названии этого уравнения благодаря его вкладу в преобразование исходного выражения к современному виду. В частности, Менделеев ввел понятие универсальной газовой постоянной.

Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Формула закона Клапейрона-Менделеева

Выше мы дали определение идеального газа, рассказали о законах, которые привели к формулировке универсального уравнения состояния. Теперь пришло время записать это уравнение:

Здесь P, V, n и T — давление, объем, количество вещества и температура, соответственно. Таким образом, произведение объема системы на давление в ней всегда находится для идеального газа в прямой пропорциональности произведению абсолютной температуры на количество вещества.

Коэффициентом пропорциональности является уже упомянутая универсальная постоянная R. Она равна 8,314 Дж/(моль*К). Если 1 моль газа нагреть на 1 кельвин, то в процессе расширения он совершит работу 8,314 Джоуля. Любопытно заметить, что универсальной величина R называется потому, что она не определяется химической природой газа. Для всех чистых газов и их смесей она принимает единственное значение.

Видео:Уравнение Менделеева - Клапейрона за 10 минут | Физика с Никитой АрхиповымСкачать

Откуда выводится изучаемое уравнение?

Выше мы уже сказали, что Клапейрон свое уравнение получил в результате банального обобщения экспериментальных результатов различных ученых. Тем не менее, закон Клапейрона-Менделеева может быть получен чисто теоретическими методами.

Одним из них является МКТ (молекулярно-кинетическая теория). МКТ рассматривает газовую систему с точки зрения концентрации частиц, распределения их скоростей, учета их масс и следование концепции идеального газа. Универсальное уравнение газа однозначно следует, если применить второй закон Ньютона к процессу упругого соударения частиц со стенками герметичного сосуда. В результате применения МКТ получается выражение:

Это равенство приводит к записанному в предыдущем пункте уравнению, если учесть следующие выражения:

Видео:62. Уравнение Клапейрона-МенделееваСкачать

Использование универсального уравнения для решения задачи

Известно, что некоторый газ под давление 2 атмосферы находится в баллоне при температуре 25 o C. Объем баллона составляет 50 литров. Какое количество вещества содержится в баллоне?

Поскольку нам известны 3 из 4-х параметров, то можно применить закон Клапейрона-Менделеева, чтобы найти величину n. Прежде чем это сделать, переведем все единицы в систему СИ:

T = 25 + 273,15 = 298,15 К;

Теперь воспользуемся формулой, получим:

n = P*V/(R*T) = 202650*0,05/(8,314*298,15) = 4,09 моль.

Хотя само значение 4,09 моль является небольшим, количество частиц газа будет гигантским. Чтобы его получить, следует n умножить на N_A=6,02*10 23 .

Видео:Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

Уравнение клапейрона менделеева когда используется

Уравнение Менделеева-Клапейрона — уравнение состояния для идеального газа, отнесенное к 1 молю газа. В 1874 г. Д. И. Менделеев на основе уравнения Клапейрона объединив его с законом Авогадро, используя молярный объем V_m и отнеся его к 1 молю, вывел уравнение состояния для 1 моля идеального газа:

pV = RT , где R — универсальная газовая постоянная,

R = 8,31 Дж/(моль . К)

Уравнение Клапейрона-Менделеева показывает, что для данной массы газа возможно одновременно изменение трех параметров, характеризующих состояние идеального газа. Для произвольной массы газа М, молярная масса которого m: pV = (М/m) . RT. или pV = N_АkT,

где N_А — число Авогадро, k — постоянная Больцмана.

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса газа и один из параметров — давление, объем или температура — остается постоянным, а изменяются только остальные два и получить теоретически газовые законы для этих условий изменения состояния газа.

Такие процессы называют изопроцессами. Законы, описывающие изопроцессы, были открыты задолго до теоретического вывода уравнения состояния идеального газа.

Изотермический процесс — процесс изменения состояния системы при постоянной температуре. Для данной массы газа произведение давления газа на его объем постоянно, если температура газа не меняется. Это закон Бойля — Мариотта.

Для того, чтобы температура газа оставалась в процессе неизменной, необходимо, чтобы газ мог обмениваться теплотой с внешней большой системой — термостатом. Роль термостата может играть внешняя среда (воздух атмосферы). Согласно закону Бойля-Мариотта, давление газа обратно пропорционально его объему: P₁V₁=P₂V₂=const. Графическая зависимость давления газа от объема изображается в виде кривой (гиперболы), которая носит название изотермы. Разным температурам соответствуют разные изотермы.

Изобарный процесс — процесс изменения состояния системы при постоянном давлении. Для газа данной массы отношение объема газа к его температуре остается постоянным, если давление газа не меняется. Это закон Гей-Люссака. Согласно закону Гей-Люссака, объем газа прямо пропорционален его температуре: V/T=const. Графически эта зависимость в координатах V-T изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изобарой. Разным давлениям соответствуют разные изобары. Закон Гей-Люссака не соблюдается в области низких температур, близких к температуре сжижения (конденсации) газов.

Изохорный процесс — процесс изменения состояния системы при постоянном объеме. Для данной массы газа отношение давления газа к его температуре остается постоянным, если объем газа не меняется. Этот газовый закон Шарля. Согласно закону Шарля, давление газа прямо пропорционально его температуре: P/T=const. Графически эта зависимость в координатах P-Т изображается в виде прямой, выходящей из точки Т=0. Эту прямую называют изохорой. Разным объемам соответствуют разные изохоры. Закон Шарля не соблюдается в области низких температур, близких и температуре сжижения (конденсации) газов.

Итак, из закона pV = (М/m) . RT выводятся следующие законы:

p = const => V/T = const — закон Гей — Люссака .

V= const => p/T = const — закон Шарля

Если идеальный газ является смесью нескольких газов, то согласно закону Дальтона, давление смеси идеальных газов равно сумме парциальных давлений входящих в нее газов. Парциальное давление — это такое давление, которое производил бы газ, если бы он один занимал весь объем, равный объему смеси.

Некоторых, возможно, интересует вопрос, каким образом удалось определить постоянную Авогадро N_A = 6,02·10 23 ? Значение числа Авогадро было экспериментально установлено только в конце XIX – начале XX века. Опишем один из таких экспериментов.

В откачанный до глубокого вакуума сосуд объемом V = 30 мл поместили навеску элемента радия массой 0,5 г и выдержали там в течение одного года. Было известно, что за секунду 1 г радия испускает 3,7·10 10 альфа-частиц. Эти частицы представляют собой ядра гелия, которые тут же принимают электроны из стенок сосуда и превращаются в атомы гелия. За год давление в сосуде выросло до 7,95·10 -4 атм (при температуре 27 о С). Изменением массы радия за год можно пренебречь. Итак, чему равна N_A?

Сначала найдем, сколько альфа-частиц (то есть атомов гелия) образовалось за один год. Обозначим это число как N атомов:

N = 3,7·10 10 · 0,5 г · 60 сек · 60 мин · 24 час · 365 дней = 5,83·10 17 атомов.

Запишем уравнение Клапейрона-Менделеева PV = nRT и заметим, что число молей гелия n = N/N_A. Отсюда:

N_A = NRT = 5,83 . 10 17 . 0,0821 . 300 = 6,02 . 10 23

PV 7,95 . 10 -4 . 3 . 10 -2

В начале XX века этот способ определения постоянной Авогадро был самым точным. Но почему так долго (в течение года) длился эксперимент? Дело в том, что радий добывается очень трудно. При его малом количестве (0,5 г) радиоактивный распад этого элемента дает очень мало гелия. А чем меньше газа в замкнутом сосуде, тем меньшее он создаст давление и тем большей будет ошибка измерения. Понятно, что ощутимое количество гелия может образоваться из радия только за достаточно долгое время.

Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Уравнение Клапейрона-Менделеева

Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Что такое уравнение Клапейрона-Менделеева

Идеальный газ — это газ, в котором пренебрегают взаимодействием молекул газа между собой.

Идеальными считают разреженные газы. Особенно близкими к идеальным считают гелий и водород.

Идеальный газ — это упрощенная математическая модель, которая широко применяется для описания свойств и поведения реальных газов при атмосферном давлении и комнатной температуре.

Давление, объем и температура — это основные параметры состояния системы, и они связаны друг с другом. Соотношение, при котором определяется данная связь, называется уравнением состояния данного газа.

Существует эквивалентная макроскопическая формулировка идеального газа — это такой газ, который одновременно будет подчиняться закону Бойля-Мариотта и Гей-Люссака, то есть:

p V = c o n s t * T

В представленном выше уравнении состоянии газа под const подразумевается количество молей.

Свойства классического и квазиклассического идеального газа описываются уравнением состояния идеального газа, которое называется уравнением Менделеева-Клапейрона, ниже представлена формула Менделеева-Клапейрона.

p V = m M R T = n R T , где m — масса газа, M — молярная масса газа, R = 8 , 314 Д ж / ( м о л ь * К ) — универсальная газовая постоянная, T — температура (К), n — количество молей газа.

Таким образом давление и объем прямо пропорциональны количеству молей и температуре.

Также уравнение Клапейрона-Менделеева можно записать в ином виде:

p V = N k T , где N — это количество молекул газа массой m , k = 1 , 38 * 10 — 23 Д ж / К — постоянная Больцмана, которая определяет «долю» газовой постоянной, приходящуюся на одну молекулу и определяется по формуле:

N = m N A M , где

N A = 6 . 02 * 10 23 м о л ь — 1 ; — это постоянная Авогадро.

Видео:Задачи по химии. Уравнение Менделеева-Клапейрона. Газовые законы. Простейшие химические расчётыСкачать

Какое значение имеет универсальная газовая постоянная

Универсальная газовая постоянная (R) — это величина, которая является константой, численно равная работе расширения одного моля идеального газа в изобарном процессе при увеличении температуры на 1 K.

Значение данной константы находится как произведение постоянной Больцмана ( k = 1 , 38 * 10 — 23 Д ж / К ) на число Авогадро ( N A = 6 . 02 * 10 23 м о л ь — 1 ) . Таким образом универсальная газовая постоянная принимает следующее значение: R = 8 , 314 Д ж / ( м о л ь * К ) .

Постоянную Больцмана используют в формулах, описывающих изучаемое явление или поведение рассматриваемого объекта с микроскопической точки зрения, тогда как универсальная газовая постоянная более удобна при расчетах, касающихся макроскопических систем, когда число частиц задано в молях.

Видео:Урок 2.Уравнение Менделеева-Клапейрона. Решение задач. База. ЕГЭСкачать

Связь с другими законами состояния идеального газа

С помощью уравнения состояния идеального газа можно исследовать процессы, в которых масса и один трех макропараметров (давление, температура или объем) — остаются неизменными.

Количественные зависимости между двумя параметрами газа при фиксированном третьем параметре называют газовыми законами, которые связывают эти параметры.

Изопроцессы — это термодинамические процессы, во время протекания которых количество вещества и один из макропараметров состояния: давление, объем, температура или энтропия — остается неизменным.

В зависимости от того, какой параметр остается неизменным различают разные процессы, которые выражаются законами, являющимися следствием уравнения состояния газа:

• изотермический процесс (T=const);
• изохорный процесс (V=const);
• изобарный процесс (p=const).

Изотермический процесс (T=const)

Процесс изменения состояния термодинамической системы при постоянной температуре называют изотермическим.

Для поддержания температуры газа постоянной необходимо, чтобы он мог обмениваться теплотой с большой системой — термостатом. Им может служить атмосферный воздух, если температура его заметно не меняется на протяжении всего процесса.

Согласно уравнению Клапейрона-Менделеева, в любом состоянии с неизменной температурой произведение давления газа на объем одно и то же, то есть постоянно:

Этот закон был открыт экспериментально английским ученым Бойлем и несколько позднее французским ученым Мариоттом. Именно поэтому он называется закон Бойля-Мариотта.

Закон Бойля-Мариотта справедлив для любых газов, а также для смеси газов (например, для воздуха).

Зависимость давления газа от объема при постоянной температуре изображается графической кривой — изотермой. Изотерма для различных температур представлена в координатах pV на рис.1. и представляет собой гиперболу.

Рис.1. Изотерма в pV — координатах.

Изохорный процесс (V=const)

Процесс изменения состояния термодинамической системы при постоянном объеме называют изохорным.

Из уравнения состояния следует, что отношение давлений газа данной массы при постоянно объеме равно отношению его абсолютных температур:

p 1 p 2 = T 1 T 2

Газовый закон был установлен экспериментально в 1787 г. французским физиком Ж. Шарлем и носит название закона Шарля: давление данной массы газа при постоянном объеме прямо пропорционально абсолютной температуре.

Так, если в качестве одного из состояний газа выбрать состояние газа при нормальных условиях, тогда

p = p 0 T T 0 = p 0 γ T

Коэффициент γ называют температурным коэффициентом давления газа. Он одинаков для всех газов.

Зависимость давления газа от температуры при постоянном объеме изображается графически прямой, которая называется изохорой (Рис.2).

Рис.2 Изображение изохоры в pT-координатах.

Изобарный процесс (p=const)

Процесс изменения состояния термодинамической системы при постоянном давлении называют изобарным.

Из уравнения Клапейрона-Менделеева вытекает, что отношение объемов газа данной массы при постоянном давлении равно отношению его абсолютных температур.

V 1 V 2 = T 1 T 2

Если в качестве второго состояния газа выбрать состояние при нормальных условиях (нормальном атмосферном давлении, температуре таяния льда) следует:

V = V 0 T T 0 = V 0 α T

Этот газовый закон был установлен экспериментально в 1802 г французским ученым Гей-Люссаком.

Закон Гей-Люссака: объем данной массы газа при постоянном давлении прямо пропорционален абсолютной температуре.

Коэффициент α называют температурным коэффициентом объемного расширения газов.

Зависимость объема газа от температуры при постоянном давлении изображается графической прямой, которая называется изобарой (Рис.3).

Рис. 3. Изобара в VT-координатах.

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Использование универсального уравнения для решения задачи

В реальности проводятся различные физико-химические процессы. Рассмотрим каким образом уравнение состояния идеального газа и законы, связанные с ним находят применение для решения физических и химических задач.

Определить давление кислорода в баллоне объемом 1 м 3 при температуре t = 27 C o . Масса кислорода 1 кг.

Так как в уравнении даны объем и температура — два из трех макроскопических параметров, а третий (давление) нужно определить, то мы можем использовать уравнение Клапейрона-Менделеева:

p V = n R T = m M R T

Не забываем перевести температуру в Кельвины:

T = t + 273 = 27 + 273 = 300 K

Молярная масса кислорода известна из таблицы Менделеева:

M ( O 2 ) = 2 * 16 = 32 г / м о л ь = 32 * 10 — 3 к г / м о л ь

Выразим из уравнения состояния давления и поставим все имеющиеся данные:

p = n R T V = m R T M V = 1 * 8 . 31 * 300 32 * 10 — 3 * 1 = 77 . 906 П а = 78 к П а

Ответ: p = 78 кПа.

Каким может быть наименьший объем баллона, содержащего кислород массой 6,4 кг, если его стенки при t = 20 C o выдерживают p = 1568 Н / с м 2 ?

Используем уравнение Менделеева-Клапейрона, из которого выражаем объем кислорода, который нужно найти:

p = n R T V = m R T M V

Молярная масса кислорода предполагается равной:

M ( O 2 ) = 2 * 16 = 32 г / м 3

Не забываем перевести температуру в Кельвины:

T = t + 273 = 20 + 273 = 293 K

Переводим давление: p = 15680000 Па

Выражаем из уравнения Клапейрона-Менделеева объем и подставляем значения, данные в условиях задачи:

V = n R T p = m R T M p = 6 . 4 * 8 . 31 * 293 15680000 * 32 * 10 — 3 = 3 . 1 * 10 — 2 м 3 = 31 л .

Используя уравнение состояния идеального газа, доказать, что плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Согласно уравнению Менделеева-Клапейрона:

p = n R T V = m R T M V

Плотность — это величина, характеризующая массу некоторого объема и находится по формуле:

ρ = m V и л и V = m ρ

Тогда p m ρ = n R T = m R T M

Откуда выражаем плотность газа:

Для водорода эта формула запишется следующим образом:

ρ H 2 = p M H 2 R T

По условию задачи водород и любой другой газ находятся при одинаковых условиях, откуда следует, что:

ρ H 2 M H 2 = p R T

Поставим последнее выражение в выражение для плотности любого газа:

ρ = M * ρ H 2 M H 2

Молярная масса водорода, исходя из таблицы Менделеева равна 2 г/моль и тогда. Молекулярная масса численно равная молярной и представляет собой массу молекулы в атомных единицах, поэтому в дальнейшем мы совершили переход к молекулярной массе.

ρ = M r * ρ H 2 2

Вывод: плотность любого газа равна половине плотности водорода ( ρ Н 2 ) , взятого при тех же условиях, умноженной на относительную молекулярную массу этого газа M_r, то есть ρ = ρ Н 2 * M r 2 .

Рассмотрим несколько задач на законы, связанные с уравнение Клапейрона-Менделеева, то есть на изотермические, изохорные, изобарные процессы.

При уменьшении давления газа в 2,5 раза его объем увеличился на 12 л. Какой объем занимал газ в начальном состоянии, если температура на протяжении всего процесса оставалась постоянной?

По условию задачи температура в ходе всего процесса оставалась постоянной, откуда следует, что у нас изотермический процесс, и мы можем воспользоваться для решения законом Бойля-Мариотта.

p 1 V 1 = p 2 V 2 , г д е p 1 – давление газа в начальном состоянии (до расширения), V 1 — объем газа в начальном состоянии, p 2 = p 1 2 . 5 — давление газа в конечном состоянии (после расширения), V 2 = V 1 + ∆ V — объем газа в конечном состоянии.

Откуда можем найти начальный объем:

p 1 V 1 = p 1 2 . 5 ( V 1 + ∆ V ) = p 1 2 . 5 V 1 + p 1 2 . 5 ∆ V

V 1 ( p 1 — p 1 2 . 5 ) = p 1 2 . 5 ∆ V

p 1 2 . 5 V 1 ( 2 . 5 — 1 ) = p 1 2 . 5 ∆ V

V 1 = ∆ V 1 , 5 = 8 л

Ответ: первоначальный объем газа был равен 8 л.

Газ находится в баллоне при температуре 400 К. До какой температуры нужно нагреть газ, чтобы его давление увеличилось в 1,5 раза?

Так как нагревание газа по условиям данной задачи происходит при постоянном объеме, значит перед нами изохорный процесс.

При изохорном процессе:

p 1 T 1 = p 2 T 2

T 2 = p 2 T 1 p 1

p 2 p 1 = 1 . 5 T 2 = 1 . 5 * T 1 = 1 . 5 * 400 = 600 K

При 27°C объем газа равен 600 мл. Какой объем займет газ при 57°C, если давление будет оставаться постоянным?

Так как давление по условию остается постоянным, то можем использовать закон Гей-Люссака.

V 1 V 2 = T 1 T 2

V_2 – искомый объем

Для правильного расчета необходимо перевести температуры из Цельсий в Кельвины:

T 1 = 273 + 27 = 300 K

T 2 = 273 + 57 = 330 K

T 2 V 1 T 1 = V 2

V 2 = ( 600 * 330 ) / 300 = 660 м л

Газ в трубе плавильной печи охлаждается от температуры t 1 = 1150 ° С д о t 2 = 200 ° С . Во сколько раз увеличивается плотность газа при этом? Давление газа не меняется.

Так как по условию задания давления газа не изменяется, значит перед нами изобарный процесс. Для решения воспользуемся законом Гей-Люссака:

V 1 V 2 = T 1 T 2

Перейдем к абсолютной температуре:

T 1 = 1150 + 273 = 1423 K

T 2 = 200 + 273 = 473 K

Масса газа: m = ρ 1 V 1 = ρ 2 V 2

Использование этих формул приводит к следующему:

🎬 Видео

Основы молекулярной физики | уравнение КлапейронаСкачать

Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Физика. Уравнение Менделеева-Клапейрона . МКТСкачать

Вывод уравнения состояния Клапейрона—МенделееваСкачать

🔴 ЕГЭ-2023 по физике. Уравнение Менделеева-Клапейрона. Закон ДальтонаСкачать

Задачи на уравнение Менделеева-Клапейрона. Ч.2. Решение задач.Скачать

Уравнение Менделеева-Клапейрона.Все виды задач на ЕГЭ.52 задачиСкачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать