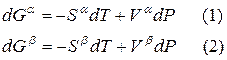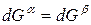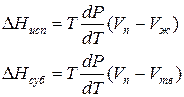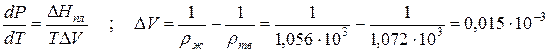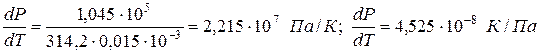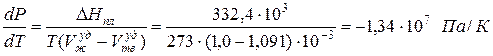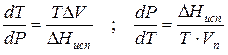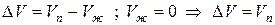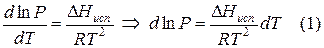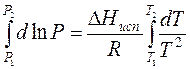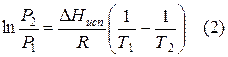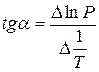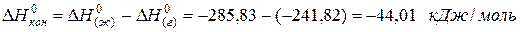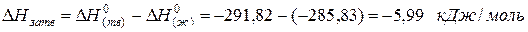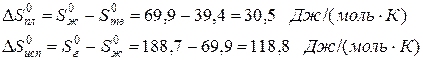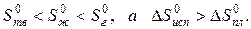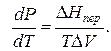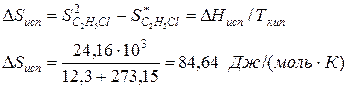Уравнение клапейрона клаузиуса и его применение к процессам плавления испарения и сублимации (4 видео)

Клапейрона–Клаузиуса

ТЕПЛОВЫЕ ЭФФЕКТЫ ФАЗОВЫХ ПЕРЕХОДОВ.

УРАВНЕНИЕ КЛАПЕЙРОНА – КЛАУЗИУСА.

Переход компонента из одной фазы в другую сопровождается выделением или поглощением теплоты, которую можно определить количественно на основе фундаментального уравнения термодинамики:

(*)

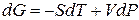
ВЫВОД И АНАЛИЗ УРАВНЕНИЯ КЛАПЕЙРОНА – КЛАУЗИУСА.

Для любого равновесного перехода вещества из одной фазы α в другую фазу β, применяя уравнение (*) к каждой из фаз, можно написать

Индексы α и β отражают принадлежность параметров к соответствующей фазе. В равновесных условиях между фазами α и β изменение энергии Гиббса отсутствует, т.е.

Приравнивая правые части уравнений 1 и 2, получим

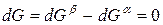
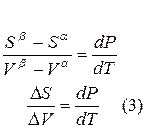
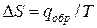
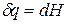
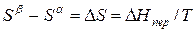
Для равновесного обратимого процесса согласно уравнениям и запишем

а уравнение (3) примет вид

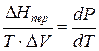
где ∆H_пер – теплота фазового перехода.

Тепловой эффект, сопровождающий фазовый переход, определяется следующим образом:

уравнение

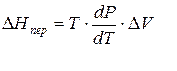
Клапейрона–Клаузиуса

где ∆V – изменение объема в результате фазового перехода; dP/dT – изменение давления в зависимости от температуры при сохранении равновесия между двумя фазами.

Уравнение Клапейрона–Клаузиуса связывает тепловой эффект процесса с изменением давления насыщенного пара, температурой и изменением объема в процессе фазового перехода.

Для процессов испарения ж→п и сублимации тв→п уравнение Клапейрона–Клаузиуса можно представить следующим образом:

где ∆H_исп , ∆H_суб – теплоты испарения и сублимации; V_п, V_ж, V_тв – мольные объемы пара, жидкости и твердого тела соответственно.

В процессе испарения и сублимации наблюдается значительное изменение удельного объема ∆V и существенное изменение величины dP/dT. При плавлении, напротив, изменение ∆V невелико, и величина dP/dT незначительна.

Пример 1. Проведем расчет по уравнению Клапейрона–Клаузиуса температуры плавления фенола Т_пл. Плотность твердого фенола ρ_тв при атмосферном давлении составляет 1,072∙10 3 кг/м 3 , а жидкого ρ_ж = 1,056∙10 3 кг/м 3 ; теплота плавления ∆H_пл = 1,045∙10 5 Дж/кг; температура замерзания 314,2 К. Определим dP/dT и температуру плавления при Р = 5,065∙10 7 Па:

Прирост температуры плавления при повышении давления на 1 атм ( 1,013∙10 5 Па) составляет 4,525∙10 -8 град/Па. При увеличении давления до 5,065∙10 7 Па температура плавления увеличивается на ∆T = (dT/dP)∆P = 4,525∙10 -8 ∙ 5,065∙10 7 = 2,29 К, т.е. составит Т_пл = 314,2+2,29 = 316,49 К.

Следует иметь в виду, что в процессе плавления у большинства веществ V_ж > V_{тв ,} тогда ∆V>0 и при повышении давления Р↑ температура плавления повышается Т↑.

Однако, такие вещества как вода (Н₂О), висмут (Bi), имеют объем твердой фазы V_тв больше, чем объем жидкой фазы V_ж уд = 10 -3 м 3 /кг и V_тв уд = 1,091·10 -3 м 3 /кг; теплота плавления ∆H_пл = 332,4 кДж/кг:

Это значение показывает, что для понижения температуры таяния льда на один градус Кельвина необходимо увеличить давление на 1,34∙10 7 Па, т.е. примерно на 134 атмосферы, что нереально, поскольку такое давление лед не выдерживает – трескается.

Таяние льда происходит в основном в результате трения и превращения работы в теплоту при скольжении конька по льду, а не за счет повышения давления на лед.

Уравнение для процесса испарения 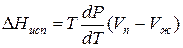можно представить в интегральном виде. Мольный объем пара значительно превосходит мольный объем жидкости, V_п >> V_{ж ,} т.е. величиной V_ж можно пренебречь. Тогда уравнение Клапейрона–Клаузиуса запишется в виде:

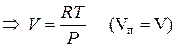
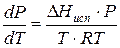
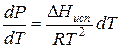
Пар подчиняется законам идеального газа: PV=RT , тогда , преобразуем уравнение, переставляя давление Р в левую часть уравнения, а dT в правую часть. Получаем:

или

Проведем интегрирование уравнения (1) в пределах от Т₁ до Т₂ и соответственно от Р₁ до Р₂ при условии, что в области невысоких давлений пара ∆Н_исп ≈ const; в результате интегрирования получим:

∆Н_исп / R = const, выносим за знак интеграла

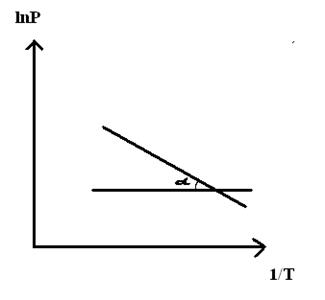
При помощи уравнения (2) можно графически определить значения теплоты испарения, если известны давления Р₁ и Р₂ и соответствующие им температуры испарения Т₁ и Т₂ . Для этого необходимо отложить на оси абсцисс значения обратной температуры, а на оси ординат – lnP.

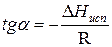
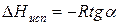
Зависимость lnP от 1/Т будет линейной, а тангенс угла наклона этой прямой равен , т.е. , а

Расчетные значения ∆Н_исп получаются с достаточной для практики точностью, не уступающей точности непосредственного измерения. Возможно использование уравнения (2) для обратного расчета, когда по значению ∆Н_исп определяют изменение давления при изменении температуры в процессе испарения.

Теплоту фазовых переходов можно определить и по величине стандартной энтальпии образования, в зависимости от фазового состояния продуктов реакции.

Пример. Лучше всего это показать на примере теплоты образования воды из газообразных кислорода и водорода, которая составляет

для водяного пара ∆Н_(г) 0 = -241,82 кДж/моль; для воды в жидком состоянии ∆Н_(ж) 0 = -285,83 кДж/моль; для льда ∆Н_(тв) 0 = -291,82 кДж/моль. Теплота конденсации воды равна:

а теплота превращения воды в лед:

Как видно, тепловой эффект фазовых переходов значительно меньше теплоты образования веществ.

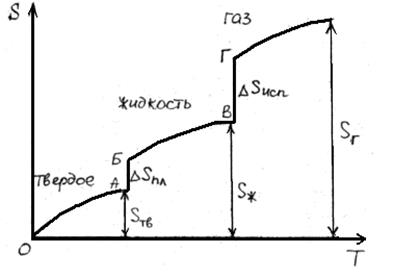
В результате фазовых переходов происходит изменение энтропии. Такие изменения в зависимости от температуры представим на рисунке.

Как известно, энтропия идеального кристалла при абсолютном нуле равна нулю. С ростом температуры атомы (ионы) флуктуировать относительно равновесного положения, число возможных способов их размещения растет, и энтропия увеличивается (ΔS>0). При достижении температуры плавления (точка А на рисунке) кристаллическая решетка разрушается скачкообразно (отрезок АБ), увеличивается термодинамическая вероятность системы W, а в соответствии с формулой S=k∙lnW (где k – постоянная Больцмана) энтропия при переходе от твердого в жидкое состояние растет. Более значительный скачок энтропии имеет место при переходе из жидкого состояния в газообразное (отрезок ВГ), когда ближний порядок расположения частиц друг относительно друга нарушается, и движение частиц становится хаотичным.

Пример. Оценим скачок энтропии на примере фазовых переходов воды:

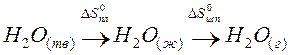
когда известны стандартные абсолютные значения энтропии S_тв 0 =39,4; S_ж 0 =69,9; S_г 0 =188,7 Дж/(моль·К).

В соответствии с рисунком для воды

По известной энтальпии фазового перехода можно рассчитать изменение энтропии в соответствии с формулой

Пример.Вычислим изменение энтропии в процессе парообразования 1 моля этилхлорида при 12,3 0 С, когда теплота испарения ∆Н_исп =24,16 кДж/моль.

Молекулярная масса 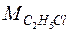= 64,5 г/моль.

В заключение отмечу, что мы рассматривали лишь фазовые переходы I рода. При фазовых переходах I рода свойства веществ, выражаемые, например, через химический потенциал, первыми производными одной из характеристических функций, изменяются скачком при непрерывном изменении соответствующих параметров: температуры, давления, объема и энтропии. При этом выделяется или поглощается теплота перехода ∆Н_пер в соответствии с уравнением Клапейрона–Клаузиуса.

Кроме них, однако, существуют фазовые переходы II рода. Они не сопровождаются выделением или поглощением теплоты, для них уравнение Клапейрона–Клаузиуса теряет смысл. Эти переходы характеризуют изменения в системе, которые не определяются объемом и запасом энергии. В этом случае первые производные одной из характеристических функций непрерывны, а вторые производные (например, теплоемкость) изменяются скачком. К фазовым переходам II рода относятся переходы парамагнетика в ферромагнетик, диэлектрика в сегнетоэлектрик, а также процессы возникновения сверхтекучести, сверхпроводимости и др.

В настоящее время насчитывается около 400 твердых минералов, для которых наблюдаются фазовые переходы II рода: рутил, анатаз, алмаз и особенно кварц, который имеет семь модификаций, причем наряду с фазовыми переходами I рода наблюдаются фазовые переходы II рода. Так, при 573 0 С и переходе модификации кварца β α теплоемкость и коэффициент линейного расширения изменяются скачкообразно (I род), но при этом поглощается теплота 10,9 кДж/моль (II род).

\|	следующая лекция ==>
ДИАГРАММА СОСТОЯНИЯ СЕРЫ.	\|	ХАРАКТЕРИСТИКА И СВОЙСТВА РАСТВОРОВ.

Дата добавления: 2016-02-02 ; просмотров: 3237 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Уравнение Клапейрона—Клаузиуса

Как мы знаем из молекулярно-кинетической теории, атомы или молекулы в жидкостях и газах находятся в состоянии постоянного движения. Время от времени отдельные молекулы жидкости, движущиеся достаточно быстро, могут «срываться» с ее поверхности. Таким образом, над любой жидкостью какое-то количество молекул данного вещества будет находиться в виде пара. Давление этих молекул, если нет посторонних примесей, называется давлением пара этого вещества. Иногда можно почувствовать это присутствие пара над жидкостью — вспомните характерное ощущение влажности на берегу моря или океана.

Нам также известно, что для перевода вещества из жидкого в газообразное состояние (см. Фазовые переходы) нужно затратить некоторую энергию. Эта энергия называется теплотой испарения или теплотой парообразования. Уравнение Клапейрона—Клаузиуса как раз и описывает отношение между теплотой испарения H , давлением пара p и температурой T вещества:

ln p = H / RT + константа

где ln p — натуральный логарифм, взятый от величины давления пара, а R — постоянная Ридберга. Температура T измеряется в кельвинах.

Первым эту зависимость в 1834 году вывел инженер-конструктор паровых машин Бенуа Клапейрон. Естественно, в силу его специальности, Клапейрона интересовала прежде всего теплота парообразования, и он использовал свое уравнение преимущественно в инженерно-прикладных целях. Для науки же уравнение теплоты фазового перехода было повторно открыто почти два десятилетия спустя Рудольфом Клаузиусом, автором формулировки второго начала термодинамики.

Чаще всего уравнение Клапейрона—Клаузиуса используется для простого расчета или измерения теплоты испарения различных веществ. Измеряя давление пара при различных температурах и нанося его на график, по одной оси которого откладывается значение lnp, а по другой — величина 1/Т, ученые по полученной линейной зависимости (углу наклона прямой) определяют теплоту испарения вещества.

Французский физик и инженер. Родился Париже. Окончил Политехническую школу и Школу минного дела. В 1820-1830 гг. работал в Институте инженеров путей сообщения в Петербурге. По возвращении во Францию стал профессором Школы мостов и дорог в Париже. Прославился как проектировщик железных дорог, конструктор железнодорожных мостов и паровозов. Доказал «теорему о трех моментах», используемую для расчета несущих конструкций с тремя и более точками опоры. Однако самый большой вклад Клапейрона в науку внес благодаря изучению тепловых процессов, за что и был избран действительным членом Академии наук Франции.

Немецкий физик. Родился в Кёслине (ныне Кошалин, Польша) в семье пастора. Учился в частной школе, директором которой был его отец. В 1848 году окончил Берлинский университет. По окончании университета предпочел физику и математику истории, которую первоначально изучал, преподавал в Берлине и Цюрихе, занимал кафедру профессора физики университетов в Цюрихе, Вюрцбурге и Бонне. С 1884 года — ректор Боннского университета. Главные работы Клаузиуса посвящены основам термодинамики и кинетической теории газов. К сожалению, тяжелые ранения, полученные во время службы добровольцем в качестве санитара во время Франко-прусской войны, помешали Клаузиусу в полной мере реализовать свой научный потенциал. Тем не менее, уже после войны и ранений, именно он сформулировал второе начало термодинамики в его современном виде.

Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнение Клапейрона — Клаузиуса

Термодинамика широко используется для изучения физических или фазовых равновесий, играющих большую роль в живых системах.

В термодинамике фазой называется совокупность однородных, одинаковых по своим свойствам частей системы.

Примеры системы, состоящей из двух фаз, находящихся в равновесии, — вода и смесь воздуха с парами воды в закрытом сосуде; алмаз и графит, представляющие собой различные твердые фазы углерода.

В зависимости от агрегатного состояния вещества системы подразделяют на гомогенные и гетерогенные.

В гомогенной (однофазной) системе отсутствуют резкие изменения физических и химических свойств при переходе от одних областей системы к другим. Примером такой системы может служить плазма крови, представляющая собой раствор различных биогенных веществ.

Гетерогенная система состоит из двух или более гомогенных частей — фаз. В качестве примера гетерогенной системы можно привести кровь, т. е. плазму с клетками (эритроцитами и лейкоцитами).

Согласно Гиббсу, химические потенциалы вещества в разных фазах равновесной системы равны между собой. На основании этого равенства можно получить соотношение, связывающее производную равновесного давления по температуре с теплотой перехода, температурой и разностью молярных объемов фаз, находя-^ щихся в равновесии:

где Q — молярная теплота фазового перехода (теплота, поглощаемая или выделяемая при фазовом переходе) при температуре Т; V₂-V- разность молярного объема вещества при переходе из фазы 1 в фазу 2; dpIdT — температурный коэффициент давления насыщенного пара при фазовом равновесии.

Это соотношение, получившее название уравнения Клапейрона — Клаузиуса, описывает переход вещества из одной фазы в другую (как в процессах испарения, плавления, сублимации).

Уравнение Клапейрона — Клаузиуса показывает, что знак производной давления по температуре зависит от того, каким изменением объема (возрастанием или уменьшением) сопровождается фазовый переход при данной теплоте.

Это уравнение применимо к любым фазовым переходам, сопровождающимся поглощением или выделением теплоты (фазовым переходам I рода).

Уравнение Клапейрона — Клаузиуса — дифференциальное уравнение кривой фазового равновесия в переменных р и Т, для решения которого необходимо знать, как изменяются величины Q, V_h V₂ в зависимости от температуры Т. Эти зависимости обычно получают эмпирически, уравнение Клапейрона — Клаузиуса решают численно.

При переходах, происходящих с поглощением теплоты (для осуществления перехода вещество нагревается, Q > 0), знак производной dp/dTопределяется знаком разности объемов V₂-V,.

Если вещество в фазе 2 занимает больший объем, чем в фазе 1, т. е. V₂> Vi, то температура перехода возрастает с увеличением давления. И наоборот, давление, с которого начинается переход, повышается с увеличением температуры. Такая зависимость характерна, например, для процессов испарения и сублимации.

Уравнение Клапейрона — Клаузиуса — один из примеров количественного выражения принципа Ле Шателье. Согласно этому принципу, если на систему, находящуюся в равновесии, подействовать извне, изменяя какое-либо из условий, определяющих равновесие, то стимулируется смещение равновесия в направлении, при котором эффект внешнего воздействия уменьшается.

Например, при нагреве в равновесной системе происходят химические реакции с поглощением теплоты, при охлаждении — с выделением теплоты.

Это положение является следствием второго начала термодинамики (К. Браун) и связано с общим условием термодинамического равновесия (максимальность энтропии термодинамической системы в состоянии равновесия).

Таким образом, принцип Ле Шателье позволяет определять направление процессов при воздействии на равновесную систему любой сложности без детального анализа всех структурных особенностей системы и условий равновесия.