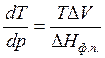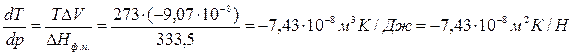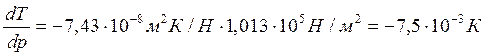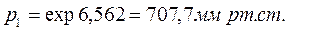Представьте себе чашку со льдом и водой. Чашка находится в комнате с температурой 0 о С. Лед и вода находятся в равновесии друг с другом, и их соотношение остается неизменным, хотя в отдельных микроскопических участках мы можем обнаружить переход воды из жидкого агрегатного состояния в твердое и наоборот. Эта картинка соответствует равновесной системе, в которой происходит обратимый процесс (плавление – кристаллизация) и нет химической реакции ( — δWm полезн = 0) .
В условиях равновесия: μж = μлед.
В соответствии с dG ≤ — δWm полезн – SdT + VdP. Для одного моля можно записать:
с учетом μж = μлед, уравнивая и вынося подобные члены получаем:
Так как тут процесс плавление – кристаллизация проходит при постоянном давлении то ∆s = hпл/T, hпл — теплота плавления одного моля вещества. Подставляя в (11.2) получаем уравнение Клаузиуса — Клайперона:
Уравнению (11.3) соответствует кривая 1 (кривая зависимости давления плавления от температуры плавления (так не говорят) или кривая зависимости температуры плавления от давления (так говорят)). Процесс плавления протекает с поглощением теплоты (эндотермический, положительный процесс) поэтому hпл > 0. (Для процесса кристаллизации наоборот). Температура положительная величина. Изменение объема может быть как положительным, так и отрицательным. В зависимости от этого кривая наклоняется в лево или в право. Аналогично в зависимости от к в уравнении у = кх.
Для процессов испарения и возгонки уравнение (11.3) удобнее представить в виде:
dlnP/dT = ∆H/T 2 R. (11.4)
Здесь все переменные положительны, поэтому dlnP/dT положительно и кривые возгонки (3) и испарения (2) наклонены вправо.

12. Фазовое равновесие в однокомпонентной системе. Диаграмма состояний
Рассмотрим и проанализируем диаграмму состояния воды (рис.1.4). Поскольку вода – единственное присутствующее в системе вещество, число независимых компонентов К = 1. В системе возможны три фазовых равновесия: между жидкостью и газом (линия ОА – зависимость давления насыщенного пара воды от температуры), твердым телом и газом (линия ОВ – зависимость давления насыщенного пара надо льдом от температуры), твердым телом и жидкостью (линия ОС – зависимость температуры плавления льда от давления). Три кривые имеют точку пересечения О, называемую тройной точкой воды; тройная точка отвечает равновесию между тремя фазами.
Рис. 1.4. Диаграмма состояния воды
В тройной точке система трехфазна и число степеней свободы равно нулю; три фазы могут находиться в равновесии лишь при строго определенных значениях температуры и давления (для воды тройная точка отвечает состоянию с Р = 6.1 кПа и Т = 273.16 К).
Кривая ОВ теоретически продолжается до абсолютного нуля, а кривая давления насыщенного пара над жидкостью ОА заканчивается в критической точке воды (Tкр = 607.46 К, Ркр = 19.5 МПа); выше критической температуры газ и жидкость не могут существовать как отдельные фазы. Кривая ОС в верхней части (при высоких давлениях) изменяет свой наклон (появляются новые кристаллические фазы, плотность которых, в отличие от обычного льда, выше, чем у воды).
Внутри каждой из областей диаграммы (АОВ, ВОС, АОС) система однофазна; число степеней свободы системы равно двум (система дивариантна), т.е. можно одновременно изменять и температуру, и давление, не вызывая изменения числа фаз в системе:
На каждой из линий число фаз в системе равно двум и, согласно правилу фаз, система моновариантна, т.е. для каждого значения температуры имеется только одно значение давления, при котором система двухфазна:
Влияние давления на температуру фазового перехода описывает уравнение Клаузиуса – Клапейрона:

Здесь ΔVфп = V2 – V1 есть изменение молярного объема вещества при фазовом переходе (причем V2 относится к состоянию, переход в которое сопровождается поглощением теплоты). Уравнение Клаузиуса – Клапейрона позволяет объяснить наклон кривых равновесия на диаграмме состояния однокомпонентной системы. Для переходов «жидкость – пар» и «твердое вещество – пар» ΔV всегда больше нуля; поэтому кривые на диаграмме состояния, отвечающие этим равновесиям, всегда наклонены вправо (повышение температуры всегда увеличивает давление насыщенного пара). Поскольку молярный объем газа много больше молярного объема того же вещества в жидком или твердом агрегатном состояниях (Vг >> Vж, Vг >> Vт), уравнение (I.109) для частных случаев испарения и возгонки примет следующий вид:

Для многих веществ скрытая теплота парообразования или возгонки постоянна в большом интервале температур; в этом случае уравнение (I.110) можно проинтегрировать:

Кривая равновесия «твердое вещество – жидкость» на диаграммах состояния воды и висмута наклонена влево, а на диаграммах состояния остальных веществ – вправо. Это связано с тем, что плотность воды больше, чем плотность льда (и плотность жидкого висмута больше его плотности в твердом состоянии), т.е. плавление сопровождается уменьшением объема (ΔV 0 и, согласно уравнению Клаузиуса – Клапейрона, увеличение давления приводит к повышению температуры плавления.
Условием равновесия в однокомпонентной системе является равенство химических потенциалов и изменений химических потенциалов для всех фаз.
Закон Гиббса. Пусть есть система из Ф фаз в которых распределены К компонентов. На систему оказывают свое воздействие N физических факторов. Для описания этой системы нам надо указать состав каждой из фаз и величины влияющих физических факторов. То есть Ф(К – 1) + N переменных. (К – 1) – потому что если фаза состоит из 3 компонентов, то нам надо задать концентрации двух. В условиях равновесия в системе химические потенциалы у каждого компонента во всех фазах между собой будут равны. И через химические потенциалы будут между собой связаны составы фаз. Это уменьшит число переменных на (Ф – 1)К.
С = Ф(К – 1) + N — (Ф – 1)К
Выражение (12.2) носит название правило фаз Гиббса.
С – число переменных, которое необходимо знать, чтобы полностью охарактеризовать систему в любой точке на диаграмме. С другой стороны число степеней свободы, переменные которые мы можем свободно менять в системе в определенных пределах без изменения числа фаз.
Вернемся к рисунку 1. В тройной точке в равновесии находятся 3 фазы, N = 2 (давление и температура), компонент один, поэтому число степеней свободы 0. Это значит что мы ни чего не можем изменить. Если мы будем подводить тепло, то оно будет расходоваться на плавления льда. И пока лед не растает система будет неизменной. Когда лед растает мы перейдем на линию 2 – испарения. Число фаз 2. число степеней свободы 1. это значит мы можем произвольно менять или Р или Т. Что-то одно, вторая переменная изменится автоматически. Меняя или Р или Т мы будем двигаться по кривой испарения. Если вся жидкость испарится то мы окажемся в области пара. Фаза одна число степеней свободы 2. То есть можно одновременно менять и Р и Т.
Видео:Фазовые диаграммы. Тройная точка. Критическое состояние вещества. 10 класс.Скачать

Физическая химия
Главная > Документ
| Информация о документе | |
| Дата добавления: | |
| Размер: | |
| Доступные форматы для скачивания: |
§ 3. Фазовые переходы. Уравнение Клапейрона-Клаузиуса
В системе, состоящей из нескольких фаз чистого вещества, находящихся в равновесии, возможны переходы вещества из одной фазы в другую. Такие переходы называются фазовыми переходами или превращениями агрегатных состояний.
Рассмотрим равновесный переход одного моля вещества из одной фазы (1) в другую (2), совершающийся при постоянных давлении и температуре. Энергии Гиббса ( G 1 и G 2 ) моля вещества в фазах 1 и 2 равны (условие равновесия). Следовательно:
G 2 = G 1 (III, 14)
Напишем уравнения (III, 13б) полных дифференциалов для энергии Гиббса одного моля чистого вещества в двух равновесных фазах 1 и 2:
dG 1 = V 1 dP – S 1 dT
dG 2 = V 2 dP – S 2 dT (III, 15)
Вычитая верхнее уравнение из нижнего, получим:
dG 2 – dG 1 = ( V 2 – V 1 ) dP – ( S 2 – S 1 ) dT
Изменения P и Т здесь были не независимыми, а такими, при которых сохранялось равновесие между фазами 1 и 2. Таким образом, между P и Т сохранялась функциональная связь, соответствующая фазовому равновесию. Поэтому, если G 1 = G 2 (равновесие при давлении P и температуре Т ), то G 1 + dG 1 = G 2 + dG 2 (равновесие при давлении P + dP и температуре T + dT ), т. е. dG l = dG 2 или dG 2 – dG 1 = 0. Следовательно
( V 2 – V 1 ) dP – ( S 2 – S 1 ) dT = 0

Взаимное превращение, фаз рассматривалось здесь как равновесное и изотермическое, поэтому:
S 2 – S 1 = S = 


Здесь 
Из уравнений (III, 16) и (III, 17) получим:

Уравнение (III, 18) называется уравнением Клапейрона — Клаузиуса и является общим термодинамическим уравнением, приложимым ко всем фазовым переходам чистых веществ, т.е. к превращениям агрегатных состояний.
При превращении одной фазы в другую такие свойства как удельный или мольный объём, внутренняя энергия и энтропия одного грамма или одного моля вещества изменяются скачкообразно. Однако отсюда не следует, что внутренняя энергия всей двухфазной системы не является в этом случае непрерывной функцией её состояния. В самом деле, система, состоявшая в начале процесса, например, из некоторого количества льда при 0°С и 1 атм, при постоянном давлении и подведении теплоты превращается в двухфазную систему лед-жидкая вода, в которой по мере поглощения теплоты масса льда постепенно и непрерывно убывает, а масса воды растет. Поэтому также постепенно и непрерывно изменяются такие свойства системы в целом как внутренняя энергия, энтальпия, энтропия и др.
§ 4. Фазовые переходы первого рода. Плавление. Испарение
Фазовые переходы, характеризующиеся равенством изобарных потенциалов двух сосуществующих в равновесии фаз и скачкообразным изменением энтропии и объема при переходе вещества из одной фазы в другую, – называются фазовыми переходами первого рода. К ним относятся агрегатные превращения – плавление, испарение, возгонка и др.
Из фазовых переходов первого рода рассмотрим плавление и испарение, представляющие более общий интерес, чем другие процессы.
Плавление. Теплота плавления – перехода твердой фазы в жидкую – всегда положительна. Объём (мольный, удельный) жидкой фазы ( V ж = V 2 ) в общем случае может быть больше или меньше объёма того же количества твердой фазы ( V т = V 1 ) . Отсюда в соответствии с уравнением (III, 18) вытекает, что величина dP / dT или обратная ей величина dT / dP , характеризующая изменение температуры с увеличением давления, может быть положительной или отрицательной. Это значит, что температура плавления может повышаться или понижаться с увеличением давления.
Так, для бензола ( t пл. = 5,4°C; 

Обратная величина dT / dP = 0,0282 
Величина dT / dP положительна для огромного большинства веществ. Она имеет отрицательное значение лишь для воды, висмута и немногих других веществ, для которых плотность жидкости при температуре плавления больше плотности твердой фазы и ( V ж – V т )
Испарение. Теплота испарения – перехода жидкой фазы в газообразную – так же, как и теплота плавления, положительна. В этом случае всегда объём (удельный, мольный) газа больше соответствующего объёма жидкости, т. е. в уравнении (III, 18) всегда V 2 > V 1 . Поэтому dP / dT , а значит, и dT / dP также всегда положительны. Следовательно, температура испарения всегда повышается с ростом давления.
При температурах, далеких от критической, плотность насыщенного пара во много раз меньше плотности жидкости, а обратная величина – мольный (удельный) объём пара во много раз больше мольного (удельного) объёма жидкости. Поэтому значением V 1 = V ж в уравнении (III, 18) можно пренебречь, и оно примет вид:

Если вдали от критической температуры насыщенный пар можно считать идеальным газом, тогда 


Теплота испарения жидкостей изменяется с температурой, не сильно убывая при средних температурах и очень сильно вблизи критической температуры, при которой 

Таблица 1. Энтальпия и энтропия испарения некоторых жидкостей при нормальной температуре кипения ( Р = 1 атм)

кал/моль

кал/моль· K
§ 5. Зависимость давления насыщенного пара от температуры
Давление насыщенного пара жидкости резко увеличивается с повышением температуры. Это видно из рис.2, на котором изображены кривые давления пара некоторых жидкостей, начинающиеся в точках плавления и оканчивающиеся в критических точках.
Рис. 2. Зависимость давления насыщенного пара некоторых жидкостей от температуры.
Функциональная зависимость давления насыщенного пара жидкости от температуры может быть выражена уравнением (III, 18), а вдали от критической температуры уравнением (III, 19).
Считая теплоту испарения (возгонки) постоянной в небольшом интервале температур, можно проинтегрировать уравнение (III, 19а)

Представив уравнение (III, 20) в виде неопределенного интеграла, получим:

где С – константа интегрирования.
В соответствии с этими уравнениями зависимость давления насыщенного пара жидкости (или кристаллического вещества) от температуры может быть выражена прямой линией в координатах 

На рис.3 изображена зависимость давления насыщенного пара некоторых жидкостей в указанных координатах, удовлетворительно укладывающаяся на прямые линии в интервале 0-100°С.
Однако уравнение (III, 21) не охватывает зависимости давления насыщенного пара от температуры во всем интервале температур – от температуры плавления до критической. С одной стороны, теплота испарения зависит от температуры, и интегрирование должно производиться с учётом этой зависимости. С другой стороны, насыщенный пар при высоких температурах нельзя считать идеальным газом. Поэтому уравнение, охватывающее зависимость P = f ( T ) в широком интервале температур, неизбежно становится эмпирическим.
Рис.3. Зависимость логарифма давления насыщенного пара некоторых жидкостей от обратной температуры.
§ 6. Сверхкритическое состояние вещества.
Сверхкритическое состояние – четвертая форма агрегатного состояния, в которое способны переходить многие органические и неорганические вещества.
Впервые сверхкритическое состояние вещества обнаружил Каньяр де ла Тур в 1822 году. Настоящий интерес к новому явлению возник 1869 году после экспериментов Т.Эндрюса. Проводя опыты в толстостенных стеклянных трубках, учёный исследовал свойства CO 2 , легко сжижающегося при повышении давления. В результате он установил, что при 31° С и 7,2 МПа , мениск – граница, разделяющая жидкость и находящийся в равновесии с ней пар, исчезает, при этом система становится гомогенной (однородной) и весь объем приобретает вид молочно-белой опалесцирующей жидкости. При дальнейшем повышении температуры она быстро становится прозрачной и подвижной, состоящей из постоянно перетекающих струй, напоминающих потоки теплого воздуха над нагретой поверхностью. Дальнейшее повышение температуры и давления не приводило к видимым изменениям.
Точку, в которой происходит такой переход, он назвал критической, а состояние вещества, находящегося выше этой точки – сверхкритическим. Несмотря на то, что внешне это состояние напоминает жидкость, в применении к нему сейчас используется специальный термин – сверхкритический флюид (от английского слова fluid , то есть «способный течь»). В современной литературе принято сокращенное обозначение сверхкритических флюидов – СКФ.
Расположение линий, разграничивающих области газообразного, жидкого и твердого состояний, а также положение тройной точки, где сходятся все три области, для каждого вещества индивидуальны. Сверхкритическая область начинается в критической точке (обозначена звездочкой), которая характеризуется непременно двумя параметрами – температурой ( Т кр . ) и давлением ( Р кр . ). Понижение либо температуры, либо давления ниже критических значений выводит вещество из сверхкритического состояния.
Факт существования критической точки позволил понять, почему некоторые газы, например, водород, азот и кислород долгое время не удавалось получить в жидком виде при повышении давления, из-за чего их называли перманентными газами (от латинского permanentis – «постоянный»). На приведённой выше диаграмме видно, что область существования жидкой фазы расположена слева от линии критической температуры. Таким образом, для сжижения какого-либо газа его необходимо сначала охладить до температуры ниже критической. У СО 2 критическая температура выше комнатной, поэтому его можно сжижать при указанных условиях, повышая давление. У азота критическая температура намного ниже: –146,95° С, поэтому, если сжимать азот, находящийся при нормальных условиях, можно достичь в конечном итоге сверхкритической области, но жидкий азот при этом образоваться не может. Необходимо сначала охладить азот ниже критической температуры и затем, повышая давление, достичь области, где возможно существование жидкости. Аналогичная ситуация для водорода, кислорода, поэтому перед сжижением их охлаждают до температуры ниже критической, и лишь затем повышают давление. Сверхкритическое состояние возможно для большинства веществ, нужно лишь, чтобы вещество не разлагалось при критической температуре. В сравнении с указанными веществами критическая точка воды достигается с большим трудом: t кр = 374,2° С и Р кр = 21,4 МПа .
Критическая точка признается как важный физический параметр вещества, такой же, как температуры плавления или кипения. Плотность СКФ исключительно низкая, например, вода в состоянии СКФ имеет плотность в три раза ниже, чем при обычных условиях. Все СКФ имеют крайне низкую вязкость.
Сверхкритические флюиды представляют собой нечто среднее между жидкостью и газом. Они могут сжиматься как газы (обычные жидкости практически несжимаемы) и, в тоже время, способны растворять многие вещества в твёрдом и жидком состояниях, что газам несвойственно. Сверхкритический этанол (при температуре выше 234° С) очень легко растворяет некоторые неорганические соли ( CoCl 2 , KBr , KI ). Диоксид углерода, закись азота, этилен и некоторые другие газы в состоянии СКФ приобретают способность растворять многие органические вещества – стеариновую кислоту, парафин, нафталин. Свойства сверхкритического СО 2 как растворителя можно регулировать – при повышении давления его растворяющая способность резко увеличивается.
Сверхкритические флюиды стали широко использовать только в 1980-х, когда общий уровень развития промышленности сделал установки для получения СКФ широко доступными. С этого момента началось интенсивное развитие сверхкритических технологий. СКФ – это не только хорошие растворители, но и вещества с высоким коэффициентом диффузии, т.е. они легко проникают в глубинные слои различных твердых веществ и материалов. Наиболее широкое применение нашёл сверхкритический СО 2 , который оказался растворителем широкого круга органических соединений. Диоксид углерода стал лидером в мире сверхкритических технологий, т.к. обладает целым комплексом преимуществ. Перевести его в сверхкритическое состояние достаточно легко ( t кр – 31° С, Р кр – 73,8 атм. ), кроме того, он не токсичен, не горюч, не взрывоопасен, к тому же, дешев и доступен. С точки зрения любого технолога он является идеальным компонентом любого процесса. Особую привлекательность ему придает то, что он является составной частью атмосферного воздуха и, следовательно, не загрязняет окружающую среду. Сверхкритический СО 2 можно считать экологически абсолютно чистым растворителем. Приведём только некоторые примеры его использования.
Кофеин – препарат, используемый для улучшения деятельности сердечно-сосудистой системы, получают из кофейных зерен даже без их предварительного измельчения. Полнота извлечения достигается за счет высокой проникающей способности СКФ. Зерна помещают в автоклав – ёмкость, выдерживающую повышенное давление, затем подают в неё газообразный СО 2 , далее создают необходимое давление (>73 атм. ), в результате СО 2 переходит в сверхкритическое состояние. Всё содержимое перемешивают, после чего флюид вместе с растворенным кофеином сливают в открытую емкость. Диоксид углерода, оказавшись в условиях атмосферного давления, превращается в газ и улетает в атмосферу, а экстрагированный кофеин остается в открытой емкости в чистом виде.
Применение СКФ оказалось весьма успешным для очистки от загрязнений электронных схем в процессе их производства, так как на них не остается никаких следов очищающего растворителя.
В связи с быстрыми темпами выработки активной части запасов легкой нефти резко возрос интерес к методам увеличения нефтеотдачи пластов. Если в 70–80 годы XX века число проектов, направленных на решение проблемы увеличения нефтеотдачи посредством нагнетания смешивающихся углеводородных растворителей, «инертных» газов и диоксида углерода было сопоставимо, то в конце XX и начале XXI столетий только метод нагнетания СО 2 имел устойчивую тенденцию роста. Эффективность применения СО 2 для повышения нефтеотдачи доказана не только экспериментальными и теоретическими работами, но и результатами многочисленных промышленных испытаний.
Не стоит забывать, что технология увеличения нефтеотдачи пластов с использованием СО 2 позволяет параллельно решать проблему консервации огромного количества выделяемого промышленностью углекислого газа.
Особенности процесса воздействия нагнетаемого CO 2 на нефтегазовую залежь зависят от его агрегатного состояния.
Превышение давления и температуры выше критических значений для углекислого газа (а это наиболее вероятная ситуация в пластовых условиях), предопределяет его сверхкритическое состояние. В этом случае CO 2 , обладающий исключительной растворяющей способностью по отношению к углеводородным жидкостям при прямом растворении в пластовой нефти, снижает её вязкость и резко улучшает фильтрационные свойства. Указанное обстоятельство даёт все основания отнести СКФ – технологии повышения нефтеотдачи пластов к одним из наиболее перспективных.
Видео:Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Уравнение Клапейрона — Клаузиуса
Процессы фазового перехода сопровождаются выделением или поглощением теплоты. Зависимость между теплотой фазового перехода и внешними условиями выражается уравнением Клапейрона – Клаузиуса:
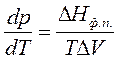
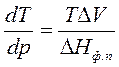
где ΔНф.п. – теплота фазового перехода; ΔV – изменение молярного объема при переходе из одной фазы в другую, 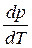
В процессе плавления (кривая ОВ, рис.3.1), объем образующейся жидкой фазы больше объема твердой фазы ( 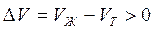
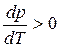
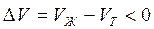
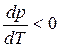
В процессе испарения и возгонки (кривые ОС и ОА на рис. 3.1 и рис. 3.2) производная 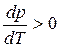
Точка О называется тройной точкой, так как в ней могут находиться в равновесии одновременно три фазы: твердая, жидкая и газообразная. Число степеней свободы в тройной точке равно: С = 3 ─ Ф = 3 ─ 3= 0. Это значит, что произвольно нельзя изменять ни один из параметров, иначе состояние равновесия в системе изменится.
Давление, которое молекулы пара, находящегося в равновесии с жидкой фазой, оказывают на стенки сосуда и на поверхность жидкости, называется давлением насыщенного пара (для краткости давление пара жидкости).
Согласно правилу фаз система с одним компонентом и двумя сосуществующими фазами имеет только одну степень свободы С = 3 ─ Ф = 3 ─ 2 = 1. Следовательно, в процессе испарения можно произвольно изменять один из параметров (либо температуру, либо давление), и при этом не изменится число и природа фаз.
Давление пара над поверхностью стабильного химического вещества (жидкости или твердого тела) определяется только температурой и не зависит от количества взятого вещества, от количества пара и от наличия и концентрации воздуха или другого газа, инертного по отношению к другому пару.
Пример 3.1. Как изменится температура плавления льда при повышении давления на 1 атм, если известно, что при 0°С теплота плавления льда равна 333,5 Дж/г, а удельные объемы воды и льда соответственно равны 1,0001·10 -6 м 3 /г и 1,0908·10 -6 м 3 /г?
Решение:
Плавление льда представляет собой фазовый переход:
твердое вещество →жидкость.
Запишем уравнение Клапейрона – Клаузиуса для процесса плавления в следующем виде:
Т=273К, ΔV=Vж – Vтв = 1,0001·10 -6 – 1,0908·10 -6 = –9,07·10 -8 м 3 /г;
При повышении давления на 1 атм температура плавления льда снизится на 0,0075 градуса.
Применение уравнения Клапейрона – Клаузиуса
К процессам испарения и возгонки
Для процессов испарения и возгонки уравнение Клапейрона-Клаузиуса удобнее представить в другой форме. Так как мольный объем вещества в газообразном состоянии значительно больше мольного объема вещества в жидком состоянии (например, объем 1 моль идеального газа составляет 22,4 л, объем 1 моль жидкой воды равен 18 мл), то изменение объема в процессе испарения (возгонки) ΔV можно считать практически равным объему пара и заменить ΔV ≈ Vп. С учетом того, что для 1 моль вещества V = RT/p, получаем уравнение Клапейрона – Клаузиуса для процессов испарения и возгонки:
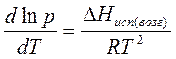
где 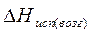
Расчет теплоты испарения и возгонки по уравнению
Клапейрона – Клаузиуса
Теплота испарения (теплота возгонки) является постоянной величиной, то есть не зависит от температуры. Величину теплоты испарения (возгонки) рассчитывают графическим и аналитическим способами.
Графический способ:
Теплоту испарения (возгонки) графическим способом можно найти, если проинтегрировать (неопределенный интеграл) уравнение Клапейрона – Клаузиуса:
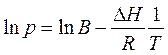
где ln В – постоянная интегрирования, зависящая от размерности, в которой выражено давление (Па, мм рт.ст., атм.).
Полученное уравнение представляет собой уравнение прямой линии, тангенс угла наклона которой равен отношению теплоты испарения (возгонки) к универсальной газовой постоянной.
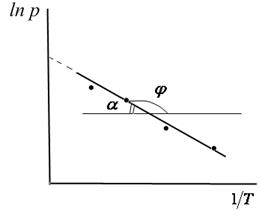 Рис.3.3. Линейная зависимость ln p от обратной температуры Рис.3.3. Линейная зависимость ln p от обратной температуры | 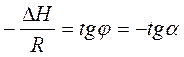 ; ; 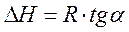 (3.8) (3.8) |
Аналитический способ:
После интегрирования уравнения (3.6) в пределах от р1 до р2 и от Т1 до Т2 получаем:
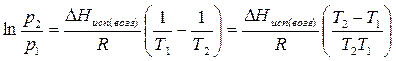
Полученное уравнение позволяет, зная давления пара вещества при двух разных температурах, рассчитать теплоту испарения (возгонки):
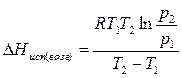
Пример 3.2. Определите давление, при котором вода закипит при 98°С.
Решение:
Кипение воды представляет собой фазовый переход:
Из справочных данных известно, что при 100°С давление насыщенного водяного пара равно 760 мм рт.ст, а удельная теплота испарения составляет 40644 Дж/моль.
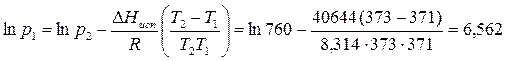
При 98°С вода закипит при давлении, равном 707,7 мм рт.ст.
Пример 3.3. Давление пара бензола при 20°С и 30°С соответственно равно 100·10 2 Па и 157·10 2 Па. Рассчитайте молярную теплоту испарения.
💡 Видео
Физическая химия # 2. Вывод уравнения Клаузиуса-КлапейронаСкачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

Уравнение КЛАПЕЙРОНА-КЛАЗИУСА | МОЛЕКУЛЯРКА (лекция) - КАРАВАЕВ В. А. ФизФак МГУСкачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Лекция №6 "Фазовые переходы. Газ Ван-дер-Ваальса"Скачать

Л7 - Теплообмен при фазовых переходах.Скачать

Теплофизика Л7. Фазовые переходы. Уравнение Клапейрона - Клаузиуса. Уравнение Ван-дер-ВаальсаСкачать

Фазовые равновесия | ФизхимияСкачать
Лекция 8Скачать

Физическая химия. Лекция 2. Термодинамика фазовых равновесийСкачать

Фазовые диаграммыСкачать

Грибов В.А. - Термодинамика и статистическая физика I - Равновесие фаз в ТД-системахСкачать

Физика 10 класс. Агрегатные (фазовые) переходы.Скачать

Грибов В.А. - Термодинамика и статистическая физика I - Фазовые переходы 2-го родаСкачать

Селиверстов А. В. - Молекулярная физика - Семинар 30Скачать

Консультация по термодинамике. Часть 2Скачать