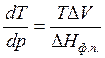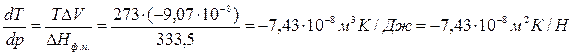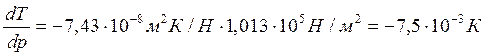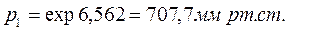Процессы фазового перехода сопровождаются выделением или поглощением теплоты. Зависимость между теплотой фазового перехода и внешними условиями выражается уравнением Клапейрона – Клаузиуса:
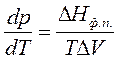
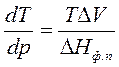
где ΔНф.п. – теплота фазового перехода; ΔV – изменение молярного объема при переходе из одной фазы в другую, 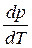
В процессе плавления (кривая ОВ, рис.3.1), объем образующейся жидкой фазы больше объема твердой фазы ( 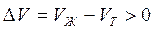
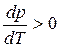
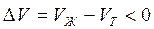
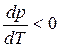
В процессе испарения и возгонки (кривые ОС и ОА на рис. 3.1 и рис. 3.2) производная 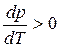
Точка О называется тройной точкой, так как в ней могут находиться в равновесии одновременно три фазы: твердая, жидкая и газообразная. Число степеней свободы в тройной точке равно: С = 3 ─ Ф = 3 ─ 3= 0. Это значит, что произвольно нельзя изменять ни один из параметров, иначе состояние равновесия в системе изменится.
Давление, которое молекулы пара, находящегося в равновесии с жидкой фазой, оказывают на стенки сосуда и на поверхность жидкости, называется давлением насыщенного пара (для краткости давление пара жидкости).
Согласно правилу фаз система с одним компонентом и двумя сосуществующими фазами имеет только одну степень свободы С = 3 ─ Ф = 3 ─ 2 = 1. Следовательно, в процессе испарения можно произвольно изменять один из параметров (либо температуру, либо давление), и при этом не изменится число и природа фаз.
Давление пара над поверхностью стабильного химического вещества (жидкости или твердого тела) определяется только температурой и не зависит от количества взятого вещества, от количества пара и от наличия и концентрации воздуха или другого газа, инертного по отношению к другому пару.
Пример 3.1. Как изменится температура плавления льда при повышении давления на 1 атм, если известно, что при 0°С теплота плавления льда равна 333,5 Дж/г, а удельные объемы воды и льда соответственно равны 1,0001·10 -6 м 3 /г и 1,0908·10 -6 м 3 /г?
Решение:
Плавление льда представляет собой фазовый переход:
твердое вещество →жидкость.
Запишем уравнение Клапейрона – Клаузиуса для процесса плавления в следующем виде:
Т=273К, ΔV=Vж – Vтв = 1,0001·10 -6 – 1,0908·10 -6 = –9,07·10 -8 м 3 /г;
При повышении давления на 1 атм температура плавления льда снизится на 0,0075 градуса.
Применение уравнения Клапейрона – Клаузиуса
К процессам испарения и возгонки
Для процессов испарения и возгонки уравнение Клапейрона-Клаузиуса удобнее представить в другой форме. Так как мольный объем вещества в газообразном состоянии значительно больше мольного объема вещества в жидком состоянии (например, объем 1 моль идеального газа составляет 22,4 л, объем 1 моль жидкой воды равен 18 мл), то изменение объема в процессе испарения (возгонки) ΔV можно считать практически равным объему пара и заменить ΔV ≈ Vп. С учетом того, что для 1 моль вещества V = RT/p, получаем уравнение Клапейрона – Клаузиуса для процессов испарения и возгонки:
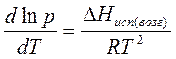
где 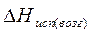
Расчет теплоты испарения и возгонки по уравнению
Клапейрона – Клаузиуса
Теплота испарения (теплота возгонки) является постоянной величиной, то есть не зависит от температуры. Величину теплоты испарения (возгонки) рассчитывают графическим и аналитическим способами.
Графический способ:
Теплоту испарения (возгонки) графическим способом можно найти, если проинтегрировать (неопределенный интеграл) уравнение Клапейрона – Клаузиуса:
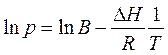
где ln В – постоянная интегрирования, зависящая от размерности, в которой выражено давление (Па, мм рт.ст., атм.).
Полученное уравнение представляет собой уравнение прямой линии, тангенс угла наклона которой равен отношению теплоты испарения (возгонки) к универсальной газовой постоянной.
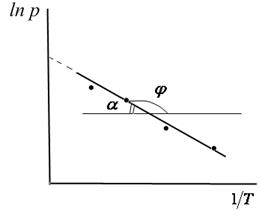 Рис.3.3. Линейная зависимость ln p от обратной температуры Рис.3.3. Линейная зависимость ln p от обратной температуры | 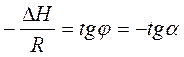 ; ; 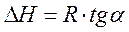 (3.8) (3.8) |
Аналитический способ:
После интегрирования уравнения (3.6) в пределах от р1 до р2 и от Т1 до Т2 получаем:
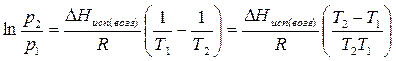
Полученное уравнение позволяет, зная давления пара вещества при двух разных температурах, рассчитать теплоту испарения (возгонки):
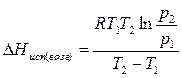
Пример 3.2. Определите давление, при котором вода закипит при 98°С.
Решение:
Кипение воды представляет собой фазовый переход:
Из справочных данных известно, что при 100°С давление насыщенного водяного пара равно 760 мм рт.ст, а удельная теплота испарения составляет 40644 Дж/моль.
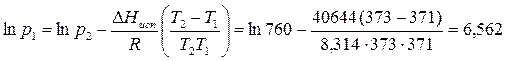
При 98°С вода закипит при давлении, равном 707,7 мм рт.ст.
Пример 3.3. Давление пара бензола при 20°С и 30°С соответственно равно 100·10 2 Па и 157·10 2 Па. Рассчитайте молярную теплоту испарения.
Видео:Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Уравнение Клапейрона—Клаузиуса
Как мы знаем из молекулярно-кинетической теории, атомы или молекулы в жидкостях и газах находятся в состоянии постоянного движения. Время от времени отдельные молекулы жидкости, движущиеся достаточно быстро, могут «срываться» с ее поверхности. Таким образом, над любой жидкостью какое-то количество молекул данного вещества будет находиться в виде пара. Давление этих молекул, если нет посторонних примесей, называется давлением пара этого вещества. Иногда можно почувствовать это присутствие пара над жидкостью — вспомните характерное ощущение влажности на берегу моря или океана.
Нам также известно, что для перевода вещества из жидкого в газообразное состояние (см. Фазовые переходы) нужно затратить некоторую энергию. Эта энергия называется теплотой испарения или теплотой парообразования. Уравнение Клапейрона—Клаузиуса как раз и описывает отношение между теплотой испарения H , давлением пара p и температурой T вещества:
ln p = H / RT + константа
где ln p — натуральный логарифм, взятый от величины давления пара, а R — постоянная Ридберга. Температура T измеряется в кельвинах.
Первым эту зависимость в 1834 году вывел инженер-конструктор паровых машин Бенуа Клапейрон. Естественно, в силу его специальности, Клапейрона интересовала прежде всего теплота парообразования, и он использовал свое уравнение преимущественно в инженерно-прикладных целях. Для науки же уравнение теплоты фазового перехода было повторно открыто почти два десятилетия спустя Рудольфом Клаузиусом, автором формулировки второго начала термодинамики.
Чаще всего уравнение Клапейрона—Клаузиуса используется для простого расчета или измерения теплоты испарения различных веществ. Измеряя давление пара при различных температурах и нанося его на график, по одной оси которого откладывается значение lnp, а по другой — величина 1/Т, ученые по полученной линейной зависимости (углу наклона прямой) определяют теплоту испарения вещества.
Французский физик и инженер. Родился Париже. Окончил Политехническую школу и Школу минного дела. В 1820-1830 гг. работал в Институте инженеров путей сообщения в Петербурге. По возвращении во Францию стал профессором Школы мостов и дорог в Париже. Прославился как проектировщик железных дорог, конструктор железнодорожных мостов и паровозов. Доказал «теорему о трех моментах», используемую для расчета несущих конструкций с тремя и более точками опоры. Однако самый большой вклад Клапейрона в науку внес благодаря изучению тепловых процессов, за что и был избран действительным членом Академии наук Франции.
Немецкий физик. Родился в Кёслине (ныне Кошалин, Польша) в семье пастора. Учился в частной школе, директором которой был его отец. В 1848 году окончил Берлинский университет. По окончании университета предпочел физику и математику истории, которую первоначально изучал, преподавал в Берлине и Цюрихе, занимал кафедру профессора физики университетов в Цюрихе, Вюрцбурге и Бонне. С 1884 года — ректор Боннского университета. Главные работы Клаузиуса посвящены основам термодинамики и кинетической теории газов. К сожалению, тяжелые ранения, полученные во время службы добровольцем в качестве санитара во время Франко-прусской войны, помешали Клаузиусу в полной мере реализовать свой научный потенциал. Тем не менее, уже после войны и ранений, именно он сформулировал второе начало термодинамики в его современном виде.
Видео:Физическая химия # 2. Вывод уравнения Клаузиуса-КлапейронаСкачать

Уравнение Клаузиуса – Клайперона и его анализ.
Представьте себе чашку со льдом и водой. Чашка находится в комнате с температурой 0 о С. Лед и вода находятся в равновесии друг с другом, и их соотношение остается неизменным, хотя в отдельных микроскопических участках мы можем обнаружить переход воды из жидкого агрегатного состояния в твердое и наоборот. Эта картинка соответствует равновесной системе, в которой происходит обратимый процесс (плавление – кристаллизация) и нет химической реакции ( — δWm полезн = 0) .
В условиях равновесия: μж = μлед.
В соответствии с dG ≤ — δWm полезн – SdT + VdP. Для одного моля можно записать:
с учетом μж = μлед, уравнивая и вынося подобные члены получаем:
Так как тут процесс плавление – кристаллизация проходит при постоянном давлении то ∆s = hпл/T, hпл — теплота плавления одного моля вещества. Подставляя в (11.2) получаем уравнение Клаузиуса — Клайперона:
Уравнению (11.3) соответствует кривая 1 (кривая зависимости давления плавления от температуры плавления (так не говорят) или кривая зависимости температуры плавления от давления (так говорят)). Процесс плавления протекает с поглощением теплоты (эндотермический, положительный процесс) поэтому hпл > 0. (Для процесса кристаллизации наоборот). Температура положительная величина. Изменение объема может быть как положительным, так и отрицательным. В зависимости от этого кривая наклоняется в лево или в право. Аналогично в зависимости от к в уравнении у = кх.
Для процессов испарения и возгонки уравнение (11.3) удобнее представить в виде:
dlnP/dT = ∆H/T 2 R. (11.4)
Здесь все переменные положительны, поэтому dlnP/dT положительно и кривые возгонки (3) и испарения (2) наклонены вправо.

12. Фазовое равновесие в однокомпонентной системе. Диаграмма состояний
Рассмотрим и проанализируем диаграмму состояния воды (рис.1.4). Поскольку вода – единственное присутствующее в системе вещество, число независимых компонентов К = 1. В системе возможны три фазовых равновесия: между жидкостью и газом (линия ОА – зависимость давления насыщенного пара воды от температуры), твердым телом и газом (линия ОВ – зависимость давления насыщенного пара надо льдом от температуры), твердым телом и жидкостью (линия ОС – зависимость температуры плавления льда от давления). Три кривые имеют точку пересечения О, называемую тройной точкой воды; тройная точка отвечает равновесию между тремя фазами.
Рис. 1.4. Диаграмма состояния воды
В тройной точке система трехфазна и число степеней свободы равно нулю; три фазы могут находиться в равновесии лишь при строго определенных значениях температуры и давления (для воды тройная точка отвечает состоянию с Р = 6.1 кПа и Т = 273.16 К).
Кривая ОВ теоретически продолжается до абсолютного нуля, а кривая давления насыщенного пара над жидкостью ОА заканчивается в критической точке воды (Tкр = 607.46 К, Ркр = 19.5 МПа); выше критической температуры газ и жидкость не могут существовать как отдельные фазы. Кривая ОС в верхней части (при высоких давлениях) изменяет свой наклон (появляются новые кристаллические фазы, плотность которых, в отличие от обычного льда, выше, чем у воды).
Внутри каждой из областей диаграммы (АОВ, ВОС, АОС) система однофазна; число степеней свободы системы равно двум (система дивариантна), т.е. можно одновременно изменять и температуру, и давление, не вызывая изменения числа фаз в системе:
На каждой из линий число фаз в системе равно двум и, согласно правилу фаз, система моновариантна, т.е. для каждого значения температуры имеется только одно значение давления, при котором система двухфазна:
Влияние давления на температуру фазового перехода описывает уравнение Клаузиуса – Клапейрона:

Здесь ΔVфп = V2 – V1 есть изменение молярного объема вещества при фазовом переходе (причем V2 относится к состоянию, переход в которое сопровождается поглощением теплоты). Уравнение Клаузиуса – Клапейрона позволяет объяснить наклон кривых равновесия на диаграмме состояния однокомпонентной системы. Для переходов «жидкость – пар» и «твердое вещество – пар» ΔV всегда больше нуля; поэтому кривые на диаграмме состояния, отвечающие этим равновесиям, всегда наклонены вправо (повышение температуры всегда увеличивает давление насыщенного пара). Поскольку молярный объем газа много больше молярного объема того же вещества в жидком или твердом агрегатном состояниях (Vг >> Vж, Vг >> Vт), уравнение (I.109) для частных случаев испарения и возгонки примет следующий вид:

Для многих веществ скрытая теплота парообразования или возгонки постоянна в большом интервале температур; в этом случае уравнение (I.110) можно проинтегрировать:

Кривая равновесия «твердое вещество – жидкость» на диаграммах состояния воды и висмута наклонена влево, а на диаграммах состояния остальных веществ – вправо. Это связано с тем, что плотность воды больше, чем плотность льда (и плотность жидкого висмута больше его плотности в твердом состоянии), т.е. плавление сопровождается уменьшением объема (ΔV 0 и, согласно уравнению Клаузиуса – Клапейрона, увеличение давления приводит к повышению температуры плавления.
Условием равновесия в однокомпонентной системе является равенство химических потенциалов и изменений химических потенциалов для всех фаз.
Закон Гиббса. Пусть есть система из Ф фаз в которых распределены К компонентов. На систему оказывают свое воздействие N физических факторов. Для описания этой системы нам надо указать состав каждой из фаз и величины влияющих физических факторов. То есть Ф(К – 1) + N переменных. (К – 1) – потому что если фаза состоит из 3 компонентов, то нам надо задать концентрации двух. В условиях равновесия в системе химические потенциалы у каждого компонента во всех фазах между собой будут равны. И через химические потенциалы будут между собой связаны составы фаз. Это уменьшит число переменных на (Ф – 1)К.
С = Ф(К – 1) + N — (Ф – 1)К
Выражение (12.2) носит название правило фаз Гиббса.
С – число переменных, которое необходимо знать, чтобы полностью охарактеризовать систему в любой точке на диаграмме. С другой стороны число степеней свободы, переменные которые мы можем свободно менять в системе в определенных пределах без изменения числа фаз.
Вернемся к рисунку 1. В тройной точке в равновесии находятся 3 фазы, N = 2 (давление и температура), компонент один, поэтому число степеней свободы 0. Это значит что мы ни чего не можем изменить. Если мы будем подводить тепло, то оно будет расходоваться на плавления льда. И пока лед не растает система будет неизменной. Когда лед растает мы перейдем на линию 2 – испарения. Число фаз 2. число степеней свободы 1. это значит мы можем произвольно менять или Р или Т. Что-то одно, вторая переменная изменится автоматически. Меняя или Р или Т мы будем двигаться по кривой испарения. Если вся жидкость испарится то мы окажемся в области пара. Фаза одна число степеней свободы 2. То есть можно одновременно менять и Р и Т.
🌟 Видео
Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Успеть за 300 секунд, #3: Уравнение Клапейрона-МенделееваСкачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Уравнение КЛАПЕЙРОНА-КЛАЗИУСА | МОЛЕКУЛЯРКА (лекция) - КАРАВАЕВ В. А. ФизФак МГУСкачать

Фазовые диаграммы. Тройная точка. Критическое состояние вещества. 10 класс.Скачать

Фазовое равновесие в однокомпонентных системах. СеминарСкачать

Урок 2.Уравнение Менделеева-Клапейрона. Решение задач. База. ЕГЭСкачать

Уравнение состояния идеального газа. 10 класс.Скачать

Теплофизика Л7. Фазовые переходы. Уравнение Клапейрона - Клаузиуса. Уравнение Ван-дер-ВаальсаСкачать

Термодинамика Л13. 2023 Сравнение уравнений состояния реальных газов. Уравнение Клапейрона-КлаузиусаСкачать

Коробов М. В. - Физическая химия. Часть 1 - Фазовые диаграммы. Фазовые переходыСкачать

Уравнение Менделеева - Клапейрона за 10 минут | Физика с Никитой АрхиповымСкачать

Лекция №6 "Фазовые переходы. Газ Ван-дер-Ваальса"Скачать

Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Фазовые равновесия | ФизхимияСкачать
Караваев В. А. - Молекулярная физика - Термодинамический потенциал. Фазовые переходыСкачать
МФ 20 апреля 2020г 11:00-11:50Скачать