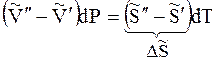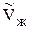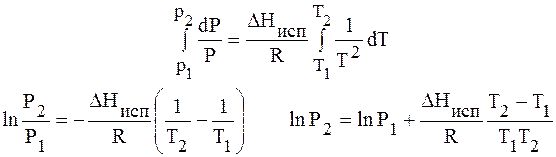Фазовые равновесия. Правило фаз Гиббса. Классификация систем. Фазовые равновесия в однокомпонентных системах. Уравнение Клапейрона-Клаузиуса. Диаграммы состояния однокомпонентных систем.
ФАЗОВЫЕ РАВНОВЕСИЯ. ПРАВИЛО ФАЗ ГИББСА.
Фазой называется гомогенная часть гетерогенной системы, имеющая во всех точках одинаковые значения интенсивных параметров, которые изменяются скачком на границе раздела фаз.
Фазовым переходом называется переход вещества из одной фазы в другую.
Фазовыми равновесиями называют равновесия в гетерогенных системах, в которых имеют место только фазовые переходы и отсутствуют химические взаимодействия между компонентами.
При переходе из одной фазы (1) в другую фазу (2) dni молей i–ого компонента (например, при конденсации пара или кристаллизации осадка), энергия Гиббса каждой из фаз изменится на величину:
для фазы 1 

для фазы 2 

Общее изменение энергии Гиббса равно:
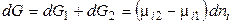
Если переход происходит в условиях равновесия при T, р = const, то



Этот вывод распространяется на любой компонент и на любую фазу системы. Итак, равновесию гетерогенных систем отвечает равенство химических потенциалов каждого компонента во всех фазах при T, p = const. Если же химический потенциал некоторого вещества в одной фазе (в одном растворе) будет больше, чем в другой фазе (в другом растворе), то вещество будет самопроизвольно переходитьиз первой фазы в другую.
Рассмотрим систему, содержащую К компонентов и состоящую из Ф фаз, находящихся в равновесии между собой. Состав каждой из фаз определяется концентрациями (К – 1) компонентов, а так как число всех фаз равно Ф, то состав всей системы определится Ф(К – 1) концентрациями всех компонентов. Для полного описания состояния системы необходимы ещё температура и давление, т. е. всего Ф (К – 1) + 2 переменных.
Условием равновесия гетерогенной системы из Ф фаз и К компонентов (как отмечалось ранее) является постоянство температуры и давления, а также равенство всех химических потенциалов каждого из компонентов во всех фазах:
. 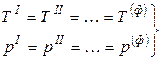
. 
Здесь верхние индексы обозначают номера фаз, нижние индексы относятся к соответствующим компонентам.
В вышеприведенных равенствах каждое значение m является функцией температуры, давления и концентрации всех компонентов. Например, для двухкомпонентной системы:
Следовательно, каждое равенство из (4.3) (например 
Обозначим через f число действительно независимых переменных. Тогда


Последнее соотношение было получено Дж. Гиббсом и носит название уравнения (правила фаз) Гиббса. Равновесные гетерогенные системы, состоящие из любого числа фаз и любого числа веществ, подчиняются правилу фаз Гиббса. Его можно сформулировать следующим образом:
число степеней свободы равновесной термодинамической системы, на которую из внешних факторов влияют только давление и температура, равно числу компонентов системы плюс два, минус число фаз:

где К — число компонентов – веществ, наименьшее число которых необходимо и достаточно для образования всех возможных фаз данной равновесной системы. Компонент является составной частью системы и может быть выделен из нее, и существовать самостоятельно;
f — число степеней свободы – число независимых термодинамических параметров, определяющих состояние системы, изменение которых в определенных пределах не вызывает исчезновения одних и образование других фаз;
число 2 — это число внешних факторов (Р и Т), которые влияют на равновесие.
Перепишем уравнение (4.5) в виде

тогда при 

т.е. максимальное число фаз в гетерогенной системе при равновесии равно числу компонентов плюс два.
Если р или Т = const, то правило фаз Гиббса запишется как
КЛАССИФИКАЦИЯ СИСТЕМ.
Можно подразделять системы по числу компонентов, степеней свободы и по числу фаз.
1). По числу компонентов ситемы классифицируют как
– однокомпонентные (или одинарные);
– двухкомпонентные (или двойные);
– трёхкомпонентные (или тройные) и т. д.
2). По числу фаз системы классифицируют как
– трёхфазные и т. д.
3). По числу степеней свободы (вариантности) системы классифицируют как
– безвариантные или нонвариантные ( f = 0);
– одновариантные или моновариантные ( f = 1);
– двухвариантные или бивариантные ( f = 2) и т. д.
Число компонентов определяют как наименьшее число составляющих частей системы, достаточное для образования всех её фаз. Число компонентов не равно числу составляющих частей лишь в тех случаях, когда между ними происходят химические взаимодействия (реакции) и в системе устанавливается химическое равновесие. В этом случае число компонентов равно числу составляющих частей системы минус число уравнений, связывающих концентрации составляющих частей.
Растворы, их общая характеристика, способы выражения состава растворов. Растворимость твердых веществ и газов в жидкостях. Идеальные растворы, законы Вант-Гоффа, Рауля и Генри. Криоскопия и эбулиоскопия. Диаграммы состояния раствор — пар для бинарных систем. Законы Коновалова, азеотропные смеси. Ограниченная взаимная растворимость жидкостей. Взаимно нерастворимые жидкости. Распределение вещества в двух несмешивающихся растворителях. Закон распределения Нернста-Шилова.
Растворы классифицируют
1). по степени дисперсности на
— истинные (молекулярные или атомные смеси компонентов);
— тонкие механические взвеси (суспензии и эмульсии).
2). по агрегатному состоянию на
3. с термодинамических позиций на
— предельно разбавленые (С2 → 0);
Физическая химия изучает термодинамические и другие свойства растворов. Коллоидные растворы и тонкие механические взвеси являются предметом исследования коллоидной химии. Свойства растворителя обычно обозначаются индексом (1), а свойства растворенных веществ – индексами (2), (3) и т. д.
Способы выражения состава растворов.
Так как количество каждого компонента может быть представлено в различных единицах измерения, то и состав раствора можно выразить несколькими способами.
1). Через мольные (молярные) доли xi:
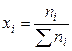
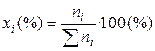
где ni – число молей i-го компонента в растворе.
2). Через объёмные доли ji:
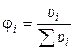
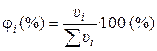
где ui ‑ объём i-ого компонента в объёме раствора u.
3). Через массовые доли 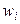
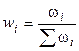
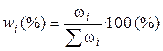
где ωi – масса i-ого компонента в растворе.
4). Через молярные концентрации (молярности) Сi:
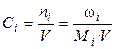
где ωi – масса i-го компонента (г), Мi – молярная масса i-ого компонента (г/моль), V – объём раствора (л), ni – число молей.
5). Через моляльные концентрации (моляльности) mi:
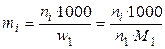
Моляльность выражает число молей i-ого компонента (растворенного вещества) в расчете на 1 кг растворителя.
6) Через молярные концентрации эквивалента (эквивалентные концентрации, нормальности) – Сi или Ni:

где фактор эквивалентности fэкв показывает, какая доля молярной массы данного вещества эквивалентна одному иону водорода в данной окислительно – восстановительной реакции.
Закон Генри.
Предельно разбавленными называются такие растворы, в которых молярная доля растворенного вещества x2 (T, xi) которую Дж. Льюис назвал термодинамической активностью i-ого компонента в растворе. В связи с этим для реальных растворов будут иметь место два равенства:

если пар подчиняется законам идеальных газов, и

если рассматривать пар как реальный газ. Активность связана с мольной долей компонента через коэффициент активности 

Величина коэффициента активности указывает на величину отклонения реальных растворов от идеальности (законов идеальных растворов).
 |  |
Если давление насыщенного пара над реальным раствором больше, чем над идеальным раствором того же состава (gi > 1), то отклонения от идеальности называются положительными. Если давление насыщенного пара над реальным раствором меньше, чем над идеальным раствором того же состава (gi
Что вызывает тренды на фондовых и товарных рынках Объяснение теории грузового поезда Первые 17 лет моих рыночных исследований сводились к попыткам вычислить, когда этот.
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Видео:Лекция «Диаграмма состояния двухкомпонентных сплавов»Скачать

Уравнение Клаузиуса – Клайперона и его анализ.
Представьте себе чашку со льдом и водой. Чашка находится в комнате с температурой 0 о С. Лед и вода находятся в равновесии друг с другом, и их соотношение остается неизменным, хотя в отдельных микроскопических участках мы можем обнаружить переход воды из жидкого агрегатного состояния в твердое и наоборот. Эта картинка соответствует равновесной системе, в которой происходит обратимый процесс (плавление – кристаллизация) и нет химической реакции ( — δWm полезн = 0) .
В условиях равновесия: μж = μлед.
В соответствии с dG ≤ — δWm полезн – SdT + VdP. Для одного моля можно записать:
с учетом μж = μлед, уравнивая и вынося подобные члены получаем:
Так как тут процесс плавление – кристаллизация проходит при постоянном давлении то ∆s = hпл/T, hпл — теплота плавления одного моля вещества. Подставляя в (11.2) получаем уравнение Клаузиуса — Клайперона:
Уравнению (11.3) соответствует кривая 1 (кривая зависимости давления плавления от температуры плавления (так не говорят) или кривая зависимости температуры плавления от давления (так говорят)). Процесс плавления протекает с поглощением теплоты (эндотермический, положительный процесс) поэтому hпл > 0. (Для процесса кристаллизации наоборот). Температура положительная величина. Изменение объема может быть как положительным, так и отрицательным. В зависимости от этого кривая наклоняется в лево или в право. Аналогично в зависимости от к в уравнении у = кх.
Для процессов испарения и возгонки уравнение (11.3) удобнее представить в виде:
dlnP/dT = ∆H/T 2 R. (11.4)
Здесь все переменные положительны, поэтому dlnP/dT положительно и кривые возгонки (3) и испарения (2) наклонены вправо.

12. Фазовое равновесие в однокомпонентной системе. Диаграмма состояний
Рассмотрим и проанализируем диаграмму состояния воды (рис.1.4). Поскольку вода – единственное присутствующее в системе вещество, число независимых компонентов К = 1. В системе возможны три фазовых равновесия: между жидкостью и газом (линия ОА – зависимость давления насыщенного пара воды от температуры), твердым телом и газом (линия ОВ – зависимость давления насыщенного пара надо льдом от температуры), твердым телом и жидкостью (линия ОС – зависимость температуры плавления льда от давления). Три кривые имеют точку пересечения О, называемую тройной точкой воды; тройная точка отвечает равновесию между тремя фазами.
Рис. 1.4. Диаграмма состояния воды
В тройной точке система трехфазна и число степеней свободы равно нулю; три фазы могут находиться в равновесии лишь при строго определенных значениях температуры и давления (для воды тройная точка отвечает состоянию с Р = 6.1 кПа и Т = 273.16 К).
Кривая ОВ теоретически продолжается до абсолютного нуля, а кривая давления насыщенного пара над жидкостью ОА заканчивается в критической точке воды (Tкр = 607.46 К, Ркр = 19.5 МПа); выше критической температуры газ и жидкость не могут существовать как отдельные фазы. Кривая ОС в верхней части (при высоких давлениях) изменяет свой наклон (появляются новые кристаллические фазы, плотность которых, в отличие от обычного льда, выше, чем у воды).
Внутри каждой из областей диаграммы (АОВ, ВОС, АОС) система однофазна; число степеней свободы системы равно двум (система дивариантна), т.е. можно одновременно изменять и температуру, и давление, не вызывая изменения числа фаз в системе:
На каждой из линий число фаз в системе равно двум и, согласно правилу фаз, система моновариантна, т.е. для каждого значения температуры имеется только одно значение давления, при котором система двухфазна:
Влияние давления на температуру фазового перехода описывает уравнение Клаузиуса – Клапейрона:

Здесь ΔVфп = V2 – V1 есть изменение молярного объема вещества при фазовом переходе (причем V2 относится к состоянию, переход в которое сопровождается поглощением теплоты). Уравнение Клаузиуса – Клапейрона позволяет объяснить наклон кривых равновесия на диаграмме состояния однокомпонентной системы. Для переходов «жидкость – пар» и «твердое вещество – пар» ΔV всегда больше нуля; поэтому кривые на диаграмме состояния, отвечающие этим равновесиям, всегда наклонены вправо (повышение температуры всегда увеличивает давление насыщенного пара). Поскольку молярный объем газа много больше молярного объема того же вещества в жидком или твердом агрегатном состояниях (Vг >> Vж, Vг >> Vт), уравнение (I.109) для частных случаев испарения и возгонки примет следующий вид:

Для многих веществ скрытая теплота парообразования или возгонки постоянна в большом интервале температур; в этом случае уравнение (I.110) можно проинтегрировать:

Кривая равновесия «твердое вещество – жидкость» на диаграммах состояния воды и висмута наклонена влево, а на диаграммах состояния остальных веществ – вправо. Это связано с тем, что плотность воды больше, чем плотность льда (и плотность жидкого висмута больше его плотности в твердом состоянии), т.е. плавление сопровождается уменьшением объема (ΔV 0 и, согласно уравнению Клаузиуса – Клапейрона, увеличение давления приводит к повышению температуры плавления.
Условием равновесия в однокомпонентной системе является равенство химических потенциалов и изменений химических потенциалов для всех фаз.
Закон Гиббса. Пусть есть система из Ф фаз в которых распределены К компонентов. На систему оказывают свое воздействие N физических факторов. Для описания этой системы нам надо указать состав каждой из фаз и величины влияющих физических факторов. То есть Ф(К – 1) + N переменных. (К – 1) – потому что если фаза состоит из 3 компонентов, то нам надо задать концентрации двух. В условиях равновесия в системе химические потенциалы у каждого компонента во всех фазах между собой будут равны. И через химические потенциалы будут между собой связаны составы фаз. Это уменьшит число переменных на (Ф – 1)К.
С = Ф(К – 1) + N — (Ф – 1)К
Выражение (12.2) носит название правило фаз Гиббса.
С – число переменных, которое необходимо знать, чтобы полностью охарактеризовать систему в любой точке на диаграмме. С другой стороны число степеней свободы, переменные которые мы можем свободно менять в системе в определенных пределах без изменения числа фаз.
Вернемся к рисунку 1. В тройной точке в равновесии находятся 3 фазы, N = 2 (давление и температура), компонент один, поэтому число степеней свободы 0. Это значит что мы ни чего не можем изменить. Если мы будем подводить тепло, то оно будет расходоваться на плавления льда. И пока лед не растает система будет неизменной. Когда лед растает мы перейдем на линию 2 – испарения. Число фаз 2. число степеней свободы 1. это значит мы можем произвольно менять или Р или Т. Что-то одно, вторая переменная изменится автоматически. Меняя или Р или Т мы будем двигаться по кривой испарения. Если вся жидкость испарится то мы окажемся в области пара. Фаза одна число степеней свободы 2. То есть можно одновременно менять и Р и Т.
Видео:09 Фаз диагр двухкомп сист 1 принципы и мех смесьСкачать
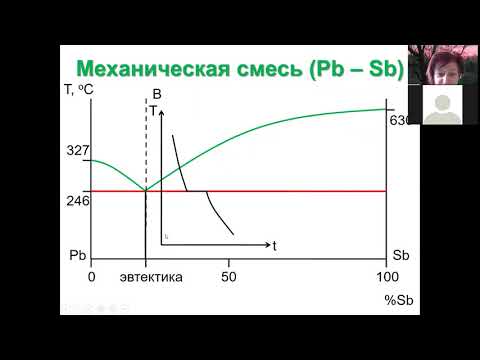
Уравнение Клапейрона – Клаузиуса, применение его к однокомпонентным системам
Простейшим типом гетерогенного равновесия является равновесие чистого вещества со своим насыщенным паром, т.е. равновесие
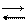
Такое равновесие можно изобразить графически:
давление насыщенного пара — температура
 |
Рис. 6.20. Зависимость давления от температуры
Давление насыщенного пара – это равновесное давление, которое создается при Т = const некоторым количеством вещества в закрытом сосуде, не содержащем посторонних газов.
Давления насыщенного пара при разных температурах дают кривую испарения.
Давления насыщенного пара над твердым веществом при разных температурах дают кривую возгонки (сублимации).
Верхняя точка кривой испарения – критическая точка.
Верхняя граница кривой возгонки – точка плавления.
Направление кривых испарения и возгонки определяется уравнением Клаузиуса – Клапейрона. Получим его.
Когда две фазы чистого вещества находятся в равновесии, их изобарные потенциалы
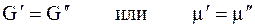
т.к. химический потенциал — это изобарный потенциал 1 моль вещества
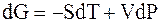
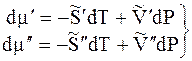
величины 
При равновесии 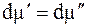
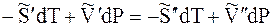
Отсюда 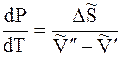
где DS – изменение энтропии при переходе 1 моль вещества из фазы 1 в фазу 2.
Из второго закона термодинамики известно, что для обратимых изотермических процессов
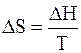
Подставим 6.244 в 6.243, получим уравнение Клапейрона –Клаузиуса (1850 г.)
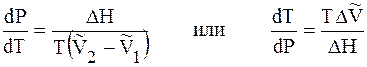
которое характеризует зависимость температуры фазового перехода от внешнего давления.
Уравнение Клапейрона – Клаузиуса описывает фазовые переходы I рода, к которым относятся переходы вещества из одного агрегатного состояния в другое, переходы из одной кристаллической модификации в другую. Среди них плавление, испарение, конденсация, возгонка,
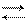
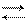
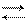
DH – теплота фазового перехода 1 моль вещества.
При фазовых переходах скачком изменяются молярная энтропия 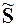
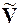
Рассмотрим некоторые конкретные случаи применения уравнения Клапейрона – Клаузиуса:
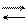
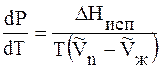
DH > 0, т.к. рассматривается переход жидкости в пар, энергия
T > 0 и 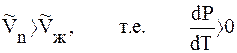
Это значит, что давление насыщенного пара растет с увеличением температуры.
Предположим, что пар подчиняется уравнению состояния идеального газа, т.е. 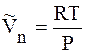
И если система далека от критической температуры, то 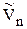
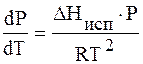
Разделим переменные и интегрируем, предполагая, что DHисп не зависит от Т.
или 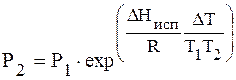
По этому уравнению можно рассчитать давление насыщенного пара Р2, зная Р1 и DHисп. Можно также рассчитать DHисп.
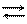
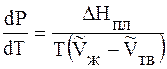
Разность DV мала, поэтому кривая плавления идет круто вверх.
Когда плотность твердого вещества больше плотности жидкого
DV > 0 и 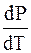
Когда плотность твердого вещества меньше плотности жидко-
У льда с повышением давления Тплав понижается, что объясняет скользкость льда (под давлением конька образуется вода, играющая роль смазки).
К = 1 S = 1 – ф + 2 ® S = 3 – ф
При равновесии в системе не может быть больше трех фаз, иначе число степеней свободы будет отрицательным числом, что не имеет физического смысла.
Т.е. в однокомпонентной системе одновременно могут существовать максимально три фазы: например, паровая, жидкая, твердая.
Диаграмму однокомпонентной системы (H2O) можно изобразить следующим образом.
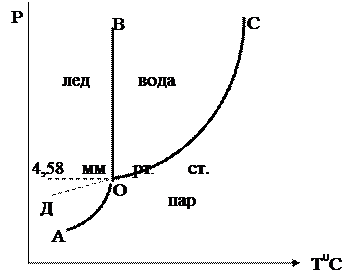 |
Рис. 6.21. Диаграмма состояния воды
В большинстве случаев за независимые переменные выбирают Р и Т.
Фазовой точкой называется точка на диаграмме, изображающая состояние одной фазы.
Совокупность фазовых точек, изображающих состояние одной фазы, называется фазовым полем
I – фазовое поле пара,
II – фазовое поле жидкости, III – твердая фаза.
Фазовые поля разделены фазовыми линиями:
ОС – соответствует равновесию двух фаз пар – жидкость,
ОА – пар – твердая фаза, ОВ – жидкость – твердая фаза.
В точке О в равновесии находятся все три фазы.
Число степеней свободы:
на фаз. поле S = 3 – 1 = 2 (два параметра можем менять),
на фаз. линии S = 3 – 2 = 1 ( один параметр можем менять),
в точке О S = 3 – 3 = 0 (параметры менять нельзя).
Если продлить ОС до Д, то ОД соответствует равновесию пар – переохлажденная жидкость.
Давление насыщенного пара над переохлажденной жидкостью больше, чем надо льдом, т.е. переохлажденная жидкость является неустойчивой (метастабильной) фазой относительно льда.
Диаграмма состояния с несколькими твердыми фазами. В однокомпонентной системе может быть только 1 паровая и 1 жидкая фаза, а твердых фаз может быть несколько. Например, сера в твердом состоянии существует в двух модификациях S(ромб) и S(монокл) с различной кристаллической решеткой, для Fe известны 4 модификации a-, b-, g- и d-, для воды известны более 5 твердых форм и т.д.
Каждая из этих модификаций выступает как отдельная самостоятельная фаза и на диаграмме ей соответствует отдельное фазовое поле.
Рассмотрим диаграмму состояния серы.
Рис. 6.22. Диаграмма состояния серы
В данном случае 4 фазовых поля, 6 фазовых линий и три тройных точки А, В и С.


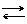
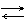
Равновесие всех четырех фаз не может быть осуществлено, т.к. число степеней свободы в этом случае S = 1 – 4 + 2 = –1, что противоречит действительности.
Энантиотропные и монотропные превращения.Многие вещества способны существовать в различных кристаллических модификациях, каждая из которых обладает определенными границами устойчивости. При этом существует некоторая температура перехода, выше которой устойчивой является одна из модификаций, а ниже – вторая.
Если превращение в точке перехода может самопроизвольно протекать как в прямом, так и в обратном направлениях, то такой переход называется энантиотропным (рис. 6.23). В этом случае между модификациями существует равновесие
Примером энантиотропного фазового перехода может служить процесс взаимного перехода серы ромбической и серы моноклинической. Энантиотропные превращения наблюдаются только в таких системах, в которых температура взаимного перехода (точка О) обеих полиморфных модификаций ниже температуры плавления этих модификаций (точки О3, О4 на рис. 6.23).
 |
Рис. 6.23. Диаграмма состояния однокомпонентной системы
с энантиотропными фазовыми превращениями
Кривая равновесия жидкость – пар СС / расположена выше точки О пересечения кривых АА / и ВВ / равновесия соответственно a- и b-полиморфных модификаций с паром. В интервале температур, соответствующих точкам А и О, более устойчива a-модификация, т.к. давление пара на участке АО ниже, чем на участке ВО. В интервале температур между точками О и О4 более устойчивой является b-модификация, которой соответствует кривая ВВ / . Между точками О4 и С / устойчивой является жидкая фаза (кривая СС / ). Участки кривых, расположенные выше кривой АОО4С / , соответствуют неустойчивым метастабильным равновесным состоянием (отрезки ВО, ОА / , СО4, О4В / ). При повышении температуры выше Т0 более устойчивой будет b-модификация и a-модификация переходит в b-модификацию. При понижении температуры ниже Т0 происходит обратный переход.
Если при любых условиях одна из модификаций более устойчива, чем вторая, то возможен переход только второй модификации в первую, но не обратно.

т.е. вторая модификация образуется из жидкости, но не из первой модификации.
Превращение модификаций, которые могут протекать только в одном направлении, называются монотропными.
В таких системах переход от модификации, устойчивой при более высоких температурах, к модификации, устойчивой при более низких температурах, невозможен. Обратный переход осуществляется и протекает тем быстрее, чем выше температура. Примерами монотропных фазовых переходов являются: превращения a-бензофенона в b-бензофенон, белого фосфора в красный, неустойчивых модификаций мышьяка и сурьмы в устойчивые модификации и др.
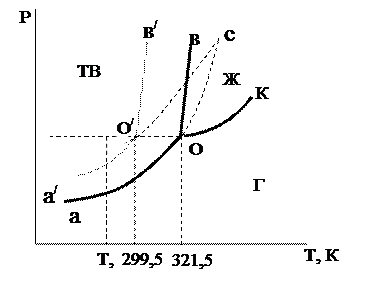 |
Рис. 6.24. Диаграмма состояния бензофенона
Рассмотрим диаграмму состояния бензофенона (С6Н5)2СО с монотропными превращения твердых фаз (рис. 6.24).
На этой диаграмме кривые аО, вО и КО изображают устойчивые двухфазные равновесия b — бензофенона. a — бензофенон является неустойчивой модификацией и может самопроизвольно превращаться в b-(C6Н5)2CО, тогда как обратный переход невозможен.
Линии аО и а¢О¢ отображают равновесия кристаллических b- и a-(C6Н5)2CО с паром, они должны пересечься в точке с, т.е. при температуре более высокой, чем температуры плавления этих модификаций (точки О и О¢). Так как перегреть кристаллическое вещество выше его температуры плавления невозможно, то линии сО и сО¢ продолжающие линии аО и аО¢, отражают физически нереальные состояния.
Рассмотренные закономерности фазовых равновесий и фазовых переходов имеют большое значение для химиков-технологов, т.к. позволяют установить оптимальный режим протекания химических и физико-химических процессов.
📺 Видео
Фазовые диаграммы. Тройная точка. Критическое состояние вещества. 10 класс.Скачать

Физика 10 класс: Уравнение Клапейрона-МенделееваСкачать

Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Уравнение состояния идеального газа. 10 класс.Скачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Фазовые диаграммыСкачать

09 Фаз диагр двухкомп сист 2 соединениеСкачать

09 Фаз диагр двухкомп сист 3 растворыСкачать

Уравнение Менделеева - Клапейрона за 10 минут | Физика с Никитой АрхиповымСкачать

Предельные вероятности состоянийСкачать

Урок 2.Уравнение Менделеева-Клапейрона. Решение задач. База. ЕГЭСкачать

Динамические диаграммы в ExcelСкачать
Решение задач на термохимические уравнения. 8 класс.Скачать

Урок 420. Дифракция света. Дифракционная решеткаСкачать

Химическая связь. Формулы Льюиса. 8 класс.Скачать

Диастолическая функция левого желудочка. NEW!Скачать

9 класс, 6 урок, Уравнение окружностиСкачать