Уравнение кирхгофа для моста уитстона

Электрический ток. Сила тока. Плотность тока

Непрерывное направленное движение электрических зарядов называют электрическим током.

Ток может течь в твердых телах, жидкостях и газах. Если среда является проводником с большим количеством свободных электронов, то течение электрического тока осуществляется за счет дрейфа этих электронов. Дрейф электронов в проводниках, не связанный с перемещением вещества, называют током проводимости.

Различают ток проводимости и конвекционный ток. Количественной характеристикой электрического тока являются сила тока I и плотность j .

Сила тока — скалярная величина, равная отношению количества электричества dq, которое за время dt, переносится через данное сечение проводника, к времени dt :

.	(1)

Постоянным называют электрический ток, сила и направление которого с течением времени не изменяются. Для постоянного тока

.	(2)

Плотность тока — векторная физическая величина, модуль которой равен отношению силы тока I к площади поперечного сечения проводника S :

.	(3)

Вектор j направлен вдоль направления тока, т. е. совпадает с направлением упорядоченного движения положительных зарядов.

Закон Ома. Сопротивление проводников.

Для того чтобы в проводнике все время шел ток, необходимо поддерживать в нем постоянное электрическое поле, т.е. на концах проводника должна быть постоянная разность потенциалов.

Сила тока в проводнике пропорциональна напряжению на его концах и обратно пропорциональна сопротивлению проводника (закон Ома для участка цепи):

.	(4)

Сопротивление проводников зависит от материала проводника, т. е. строения его кристаллической решетки. Для однородного цилиндрического проводника длиной l и площадью поперечного сечения S сопротивление определяется по формуле

.	(5)

где r — удельное сопротивление проводника. Единица удельного сопротивления — омметр (Ом•м).

Величина g=1/R , обратная сопротивлению, называется проводимостью. Единица электрической проводимости — Сименс (См).

Величина g =1/ r , обратная удельному сопротивлению, называется удельной электрической проводимостью проводника. Единица удельной электрической проводимости — (См/м).

Закон Ома можно представить в дифференциальной форме

.	(6)

Выражение (6), связывающее плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке

Обобщённый закон Ома имеет вид

.	(7)

где j 1 и j 2 – потенциалы в начальной и конечной точках участка, e – ЭДС, R – сопротивление участка, I – ток на участке цепи.

В замкнутой цепи ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем участках цепи, так как при перемещении по замкнутой цепи заряд возвращается в исходное положение — в точку с тем же потенциалом. Тогда

.	(8)

ЭДС, как и сила тока, — величина алгебраическая. Если ЭДС способствует движению положительных зарядов в выбранном направлении, то она считается положительной. Если ЭДС препятствует движению положительных зарядов, то она считается отрицательной. Соединение источников в батарею может быть последовательным и параллельным.

Соединение проводников. Зависимость сопротивления проводников от температуры

Проводники в электрической цепи могут соединяться последовательно (рис.1) или параллельно (рис.2).

Рис. 1. Последовательное соединение проводников

При последовательном соединении сила тока во всех частях одинакова. Общее напряжение равно сумме напряжений на отдельных участках:

.

Отсюда следует, что общее сопротивление цепи, состоящей из последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников:

.	(9)

При параллельном соединении проводников сила тока в неразветвленной части цепи равна сумме сил токов, текущих в параллельных участках:

Рис. 2. Параллельное соединение проводников

.

Падения напряжения в параллельно соединенных участках одинаковы.

Отсюда следует что, общее сопротивление R параллельно соединенных проводников цепи рассчитывается следующим образом:

.	(10)

Удельное электрическое сопротивление проводника зависит не только от рода вещества, но и от его состояния. Зависимость удельного сопротивления r от температуры имеет вид:

.

где r 0 — удельное сопротивление при 0°С; t — температура (по шкале Цельсия); a — температурный коэффициент сопротивления, характеризующий относительное изменение сопротивления проводника при нагревании его на 1°С или 1K:

Температурные коэффициенты сопротивления веществ различны при разных температурах. Однако для многих металлов изменение a с температурой не очень велико. Для всех чистых металлов a» 1/273 1/К (или 1/°С).

Правила Кирхгофа

В общем случае на практике часто приходится рассчитывать сложные разветвленные электрические цепи, содержащие узлы (рис.3).

Рис. 3. Соединение проводников в узел

Узлом А в разветвленной цепи называют точку, в которой сходится не меньше трех проводников.

Алгебраическая сумма токов, сходящихся в узле, равна нулю (первое правило Кирхгофа):

.	(11)

Токи, подходящие к узлу, считаются положительными, а отходящие — отрицательными.

Обобщением закона Ома является второе правило Кирхгофа, оно относится к любому замкнутому контуру разветвленной электрической цепи: в любом замкнутом контуре разветвленной цепи алгебраическая сумма ЭДС равна алгебраической сумме произведений токов на сопротивления соответствующих участков этого контура:

.	(12)

где m — число участков в замкнутом контуре, n — число источников тока в этом контуре.

Если при решении уравнений сила тока получилась отрицательной, то необходимо изменить условное направление этого тока на противоположное, сохраняя найденное значение силы тока неизменным.

Мост Уитстона

Для точных измерений сопротивлений в лабораторных условиях широко применяются мосты постоянного тока. Мостовая схема изображена на (рис.4). Сопротивления R 1 , R 2 , R 3 и R 4 называются плечами моста. В диагональ ab моста включается источник постоянного напряжения, в диагональ cd – измерительный прибор (обычно гальванометр магнитоэлектрической системы).

Рис. 4. Мостовая схема

Мост называется уравновешенным, если потенциалы точек c и d равны при подключении источника питания. При этом стрелка гальванометра стоит на нуле.

Для уравновешенного моста справедливы следующие соотношения: I 1 R 1 =I 3 R 3 , I 2 R 2 =I 4 R 4 и I 1 =I 2 , I 3 =I 4 . Отсюда

.

Если R 1 =R x неизвестное сопротивление, а R 2 , R 3 , R 4 образованы магазинами сопротивлений то

.	(13)

Уравновешенный мост позволяет измерять сопротивления с большой точностью.

В зависимости от конструкции различают магазинные и реохордные мосты Уитстона. В реохордных мостиках сопротивления R 3 , R 4 образованы проволокой натянутой вдоль линейки со шкалой (реохорд), вдоль проволоки может передвигаться подвижный контакт d. При перемещении контакта d, будут изменяться сопротивления плеч ad и db ( R 3 и R 4 ).

Причём

.

где L 1 и L 2 – длины плеч ad и db соответственно.

Помощь в написании монографии

ЧертежиСмотреть онлайн silvia saint порно видео.

Курс лекций и лабораторных по физике

ЛАБОРАТОРНАЯ РАБОТА N 226

ОПРЕДЕЛЕНИЕ СОПРОТИВЛЕНИЯ ПРОВОДНИКОВ МОСТОМ ПОСТОЯННОГО ТОКА ТИПА МВЛ – 47

Описание мастиковой схемы. Правила Кирхгофа. Мостиковая схема постоянного тока, называемая мостиком Уитстона, состоит из четырех сопротивлений Rx, R, R1, R2 , соединенных в четырехугольник АВСД (рис.1), в одну диагональ которого включен гальванометр 0, а в другую — источник тока . Участок схемы СД, содержащий гальванометр, называется мостиком. Весь процесс измерений при помощи мостиковой схемы связан с требованием отсутствия тока в мостике, отсюда и распространение названия мост на всю схему. Если в мостике ток отсутствует, то мостиковая схема (мост) считается уравновешенной.

Применим к мостиковой схеме правила Кирхгофа. Первое правило: алгебраическая сумма токов, сходящихся в узле равна нулю, т.е.

Узлом электрической схемы принято называть точку схемы, в которой сходится более чем два проводника. В мостиковой схеме (рис.1) четыре узла: А,С,Д и В. При записи первого правила Кирхгофа придерживаются следующего правила знаков; ток, текущий к узлу имеет знак плюс (ток положительный), а ток, текущий от узла, имеет знак минус (ток отрицательный).

Первое правило Кирхгофа для узла С:

или (1)

если мост уравновешен

Первое правило Кирхгофа для узла D:

или если (2)

Второе правило Кирхгофа; алгебраическая сумма произведений токов на сопротивления в ветвях замкнутого контура равна алгебраической сумме ЭДС, встречающихся в этом контуре:

При записи второго правила Кирхгофа придерживаются следующего правила знаков: токи, текущие вдоль выбранного направления обхода в контуре (например, против часовой стрелки), имеют знак плюс , а токи, текущие против направления обхода, имеют знак минус. Соответственно этому ЭДС, которые действуют по выбранному направлению обхода в контуре, считают положительными, а против направления обхода отрицательными. При этом за направление действия ЭДС источника тока в контуре принимается направление от положительного полюса.

Второе правило Кирхгофа для контура ВСДВ (обход в контуре против часовой стрелки)

или

если (3)

Второе правило Кирхгофа для контура САДС:

или

(4)

Деление равенства (3) на (4) с учетом равенства (1) и (2), дает следующее соотношение между сопротивлениями уравновешенного моста, составляющими так называемые плечи моста

(5)

Соотношение (5), являющееся условием равновесия моста, позволяет определить любое из четырех сопротивлений, включенных в плечи моста, если известны три других сопротивления. Например,

Rх=R (6)

Мост постоянного тока типа МВЛ — 47 представляет собой измерительный прибор, который в принципе ничем не отличается от моста Уитстона, описанного в работе N 214. Принципиальная схема моста (см. рис.1a) состоит из четырех сопротивлений: А, X, В и R. Сопротивления А и В составляют так называемые «плечи отношения» моста, а сопротивление R — «плечо сравнения». В противоположные вершины схемы включаются: источник тока Б и гальванометр Г -указатель равновесия моста. Условием равновесия моста (условием от­сутствия тока через гальванометр) служит выполнение следующего равен­ства:

что позволяет определить одно из четырех сопротивлений, если известны три других.

На лицевой панели прибора, электрическая схема которого изображена на рис.2, смонтированы:

Пять декадных переключателей рычажного магазина, образующего «плечо сравнения» моста. На четырех переключателях (под панелью ) установлено по 9 катушек, каждая сопротивлением 1, 10, 100, 1000 Ом, на пятом переключателе — 10 спиралей, сопротивлением 0,1 Ома каждая.

2. Контактные пластины и 10 контактов, на которых (под панелью) установлены два комплекта катушек сопротивлением 1, 10, 100, 1000, 10000 Ом, образующие «штепсельные магазины» «плеч отношения» моста А и В.

3. Кнопки Б и Г – для включения источника тока (Б) и гальванометра (Г).

4. Зажимы «Х» — для подключения измеряемого сопративления.

5. Зажимы «Г» — для подключения гальвонометра.

6. Зажимы «Б» для подключения источника тока.

ПОДГОТОВКА ПРИБОРА К ИЗМЕРЕНИЯМ

1. К зажимам «Г» присоединить нуль-гальванометр, а к зажимам «Б» присоединить источник тока.

2. К зажимам «X» присоединить измеряемое сопротивление.

3. Зная порядок величины измеряемого сопротивления (указано на сопротивлении), установить штепсели магазинов А и В в гнезда согласно таблице N 1.

В приборе предусмотрены два способа (см. рис. 3) установки штепселей. На рис.3 положение штепселя магазина А соответствует сопротивлению 100 Ом, а положение штепселя магазина В — сопротивлению 1000 Ом. Согласно таблице N 1 изображенное положение штепселей должно быть при определении сопротивлений, порядок величины которых 102- 103 Ом.

Измерение сопротивлений мостом сводится к процессу уравновешивания этого моста с последующим вычислением неизвестного сопротивления по формуле. Введение сопротивлений «плеч отношения» А и В, выполненное в подготовительной части работы, является началом этого процесса. Окончательно мост уравновешивается введением сопротивления «плеча сравнения» R, выполняемого в виде рычажного магазина. Для это­го: нажать кнопку Б, а затем кратковременно кнопку Г.

Руководствуясь стороной отклонения стрелки гальванометра, на рычажном магазине установить такое сопротивление R, при котором после нажатия кнопки Б и Г стрелка гальванометра будет оставаться не -подвижной. Отсутствие тока через гальванометр соответст­вует равновесному состоянию моста. Уравновесив мост при сопротивлении Х1 в его схеме можно вычислить это неизвестное сопротивление по формуле:

Х= ,

где А и В — сопротивления, установленные на штепсельных магазинах «плеч отношения» моста, а R — сопротивление, установленное на рычажном магазине «плеча сравнения». Сопротивление Х следует записать с точностью до десятой доли Ома, ибо рычажный магазин позволяет вводить сопротивления, величина которых составляет десятые доли Ома. Данная работа предусматривает определение двух неизвестых сопротивлений (Х1 и Х2 ) кроме того, определение сопротивлений, получаемых при последовательном (X/ ) и параллельном их соединении (Х//). Ввиду того, что введение сопротивлений А и В требует значения порядка величины измеряемого сопротмивления, X/ и Х// следует предварительно вычислить по соответствующим формулам:

или =

Чтобы убедиться в правильности этих формул, сопротивления Х/ и Х// следует определить с помощью моста. Полученные с помощью моста результаты последовательного и параллельного соединения необходимо сопоставить с величинами сопротивлений, рассчитанных по формуле (2).

ТАБЛИЦА ДЛЯ ЗАПИСИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

ТАБЛИЦА ДЛЯ СОПОСТАВЛЕНИЯ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ И ВЫЧИСЛЕНИЙ

Х

1. Начертить и описать принципиальную схему моста.

2. Опишите электрическую схему моста типа МВЛ — 47, как выполнены «плечи моста»?

3. Выведите условие равновесия моста.

4. Каков процесс уравновешивания моста МВЛ — 47?

5. Выведите формулы последовательного и параллельного соединений сопротивлений.

Лабораторная работа № 254

Приборы и принадлежности: лабораторная установка с тороидальным трансформатором на кольцевом сердечнике, осциллограф, генератор сигналов звуковой частоты.

Цель работы: изучение поведения ферромагнетиков во внешнем магнитном поле, получение петли гистерезиса, определение работы перемагничивания единицы объема ферромагнетика.

Многие вещества, будучи помещенными в магнитное поле с индукцией , изменяют величину этого поля, причем . Такие вещества называются магнетиками. Безразмерный коэффициент  называется магнитной проницаемостью и характеризует степень изменения внешнего поля магнетиком. Обычно внешнее поле характеризуется напряженностью магнитного поля , где , поэтому

(1)

Изменение поля в веществе объясняется наличием дополнительного поля, создаваемого магнитными моментами молекул и атомов. Если величина магнитных моментов молекул не зависит от Н, то при внесении в поле эти моменты ориентируются по Н и усиливают поле. К таким ве­ществам относятся, например, парамагнетики, для которых . Если же магнитные моменты молекул наводятся внешним полем, то они ориентируются против Н и уменьшают поле. В этом случае , а такие вещества называют диамагнетиками. Для обоих этих типов магнетиков близко к единице, а магнитные моменты молекул и атомов создаются в основном за счет орбитального движения электронов (токи Ампера). Для третьего класса веществ, называемых ферромагнетиками (железо, никель кобальт), при не слишком высоких температурах может быть порядка тысячи и более. Это объясняется существованием в них областей с высокой степенью намагниченности за счет упорядоченной ориентации собственных магнитных моментов атомов. Существование таких областей — доменов — соответствует минимальной энергии атомной структуры. При отсутствии намагниченности образца магнитные моменты доменов ориентированы беспорядочно. Если же ферромагнетик помещен во внешнее магнитное поле, то магнитные моменты доменов стремятся повернуться по полю, тем самым увеличивая его. При достаточно большой величине внешнего поля магнитные моменты всех доменов направлены по полю, а ферромагнетик намагничен до насыщения. Из сказанного следует, что магнитная проницаемость ферромагнетика зависит от внешнего поля. Примерная зависимость и B от Н изображена на рис. 1 и рис. 2.

Ход кривых легко понять, если наряду с формулой (1) использовать соотношение

(1а)

где — вектор намагниченности (магнитный момент единицы объема):

— магнитные моменты отдельных доменов.

На участке суммарное поле, характеризуемое вектором магнитной индукций , растет довольно быстро, т. к. быстро возрастает .

При ферромагнетик намагничивается до насыщения и далее B увеличивается довольно медленно, а зависимость от H на этом участке является линейной. Значение зависит от температуры. При определенном для каждого ферромагнетика значении температуры Tk (точка Кюри) происходит разрушение доменов и ферромагнетик превращается в парамагнетик. Если намагнитить ферромагнетик до насыщения (точка 1 на рис. 3), а затем уменьшить напряженность поля до нуля, ферромагнетик будет иметь остаточную намагниченность (точка 2). Чтобы индукция B стала равной нулю (точка 3), необходимо приложить об­ратное по направлению поле величина которого называется коэрцитивной силой. При дальнейшем увеличении поля H ферромагнетик можно снова намагнитить до насыщения (точка 4). Повторяя весь процесс в обратном направлении, (кривая 4-5-6-1), получим замкнутую петлю гистерезиса. Полученная петля является максимальной. Если намагничивать ферромагнетик, не доводя его до насыщения, то получится семейство петель гистерезиса меньшего размера. Соединив вершины этих петель (точки 1), мы получим кривую намагничивания, показанную на рис. 2.

На перемагничивание ферромагнетика затрачивается энергия, идущая на его нагревание. За один цикл перемагничивания единицы объема ферромагнетика внешние силы совершают определенную работу А. Покажем, что эта работа численно равна площади петли гистерезиса (в единицах В и Н , т.е. Тл А/м). Если по соленоиду или тороиду с ферромагнитным сердечником идет ток I, то напряженность и индукция магнитного поля в сердечнике могут быть определе­ны по формуле:

, , (2)

где N — число витков соленоида, l- его длина.

Если ток в обмотке изменяется, то меняются H, B и потокосцепление (суммарный магнитный поток)

(3)

где Ф = В S — магнитный поток через один виток с площадью S. Согласно общим правилам работа, необходимая для увеличения суммарного магнитного потока на величину , равна

(4)

Учитывая, и , получаем

(5)

Разделив полученное выражение на объем ферромагнетика , получим работу, отнесенную к единице объема

(6)

Рис. 4. Работа перемагничивания ферромагнетика

Правила Кирхгофа

Рассмотренные нами законы постоянного тока позволяют рассчитать токи в сложных разветвлённых электрических цепях. Эти расчёты упрощаются, если пользоваться правилами Кирхгофа.

Правил Кирхгофа два: правило токов и правило напряжений.

Правило токов относится к узлам цепи, то есть, к таким точкам схемы, где сходятся не менее трёх проводников (рис. 7.4.). Правило токов гласит: алгебраическая сумма токов в узле равняется нулю:

. (7.9)

При составлении соответствующего уравнения, токи, втекающие в узел, берутся со знаком плюс, а покидающие его — со знаком минус. Так, для узла А (рис. 7.3.) можно записать:

Это первое правило Кирхгофа является следствием уравнения непрерывности (см. (6.7)) или закона сохранения электрического заряда.

Правило напряжений относится к любому замкнутому контуру разветвлённой цепи.

Выделим, например, в разветвлённой сложной цепи замкнутый элемент 1-2-3-1 (рис. 7.5.). Произвольно обозначим в ветвях контура направления токов I₁, I₂, I₃. Для каждой ветви запишем уравнение закона Ома для неоднородного участка цепи:

Участок .

Здесь R₁, R₂, R₃ — полное сопротивление соответствующих ветвей. Сложив эти уравнения, получим формулу второго правила Кирхгофа:

Правило напряжений формулируется так: в любом замкнутом контуре алгебраическая сумма падений напряжения равна алгебраической сумме э.д.с., встречающихся в этом контуре:

. (7.10)

При составлении уравнения (7.10) второго правила Кирхгофа задаются направлением обхода: в нашем примере — по часовой стрелке. Токи, совпадающие с направлением обхода, берутся со знаком плюс (I₁), токи противоположного направления — со знаком минус (–I₂, –I₃).

Э.д.с. источника берётся со знаком плюс, если он создаёт ток, совпадающий с направлением обхода (+e₁, +e₂, +e₅). В противном случае э.д.с. отрицательна (–e₃, –e₄).

В качестве примера составим уравнения правил Кирхгофа для конкретной электрической схемы — измерительного моста Уитстона (рис. 7.6.). Мост образуют четыре резистора R₁, R₂, R₃, R₄. В точках A и B к мосту подключен источник питания (e, r), а в диагонали BD — измерительный гальванометр с сопротивлением R_g.

В схеме четыре узла: точки A, B, C, D. Для трёх из них составим уравнения первого правила Кирхгофа — правила токов:

Для трёх контуров цепи ABDA, BCDB и ADCeA составим уравнения второго правила Кирхгофа. Во всех контурах направление обхода по часовой стрелке.

Таким образом, мы получили систему шести уравнений, решая которую можно найти все шесть неизвестных токов.

Но чаще мост Уитстона используется для измерения неизвестного сопротивления R_x º R₁. В этом случае резисторы R₂, R₃ и R₄ — переменные. Меняя их сопротивления, добиваются того, чтобы ток в измерительной диагонали моста оказался равным нулю I_g = 0. Это означает, что:

Учитывая эти упрощающие обстоятельства, приходим к выводу, что:

,

.

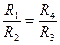
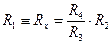
Замечательно, что для определения неизвестного сопротивления нужно знать лишь сопротивления резисторов моста R₂, R₃ и R₄. Э.д.с. источника, его внутреннее сопротивление, как и сопротивление гальванометра при таком измерении не играют никакой роли.

Дата добавления: 2015-08-08 ; просмотров: 848 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

📺 Видео