Уравнение кирхгофа для контуров трансформатора

Простейший трансформатор представляет собой совокупность двух обмоток, размещенных на общем магнитопроводе (рис. 35.1, а).

Рис. 35.1 — Трансформатор и его схема замещения

К его первичной обмотке подводится напряжение источника питания, а ко вторичной – подключается нагрузка. Одноименными зажимами обмоток являются их верхние выводы. Ток первичной обмотки I1 создает в магнитопроводе магнитный поток Ф1, который в свою очередь во вторичной обмотке вызывает появление тока I2. Создаваемый им магнитный поток Ф2 в соответствии с принципом Ленца препятствует потоку Ф1, т.е. направлен ему навстречу. Направление тока I2, соответствующее показанному на схеме потоку Ф2, определяем по правилу правой руки.

Мы будем рассматривать трансформатор, не имеющий ферромагнитного сердечника. Такие трансформаторы применяются при высоких частотах и в специальных электроизмерительных устройствах. Катушки с ферромагнитными сердечниками имеют нелинейные характеристики и здесь не рассматриваются.

Электрическая схема замещения трансформатора изображена на рис. 35.1, б. На схеме указаны: R1, X1, R2, X2 и – сопротивления первичной и вторичной обмоток трансформатора, RН и XH – сопротивления нагрузки. Введем обозначения: R22=R2+RH и X22=X2+XH – суммарные активное и реактивное сопротивления вторичной цепи трансформатора, Z1=R1+jX1, Z2=R2+jX2, ZH=RH+jXH, Z22=R22+jX22 – комплексные сопротивления соответствующих участков.

Запишем уравнения второго закона Кирхгофа для первичной и вторичной цепей трансформатора, учитывая, что его обмотки имеют встречное включение:

Обозначив I1jXM=E2M, второе уравнение системы (35.1) можно записать так:

Физически E2M – это ЭДС, которая наводится во вторичной обмотке переменным магнитным полем первичной обмотки. С учетом этого уравнение можно прочитать так: ЭДС, наведенная во вторичной обмотке трансформатора, равна сумме падений напряжений на всех элементах его вторичного контура. Подставляя I2ZH=U2 , получим: U2=E2M-I2Z2 . Смысл последнего уравнения заключается в следующем: напряжение на вторичных зажимах трансформатора меньше эдс, наведенной во вторичной обмотке, на величину падения напряжения на ее сопротивлении.

На рис. 35.2 изображена векторная диаграмма трансформатора. Ее построение начинаем со вторичного тока I2. Ориентируясь на его направление, проводим векторы напряжений на всех элементах вторичной цепи. Их сумма равна ЭДС E2M. Так как в формуле, определяющей ее величину, присутствует множитель j, поворачивающий вектор на четверть оборота, то ток проводим под углом 90° к E2M в сторону отставания. Определив направление I1, строим векторы I1R1 и I1jX1 , которые в сумме с I2jXM – дают U1.

Рис. 35.2 — Векторная диаграмма трансформатора

Для анализа работы трансформатора применяют различные эквивалентные схемы. Рассмотрим некоторые из них.

Соединив между собой два нижних зажима трансформатора (режим его работы при этом не изменится) и произведя развязку индуктивных связей, придём к Т-образной эквивалентной схеме (рис. 35.3).

Рис. 35.3 — Получение двухконтурной (Т-образной) эквивалентной схемы

Из второго уравнения системы выразим ток I2 и подставим в первое уравнение той же системы:

Последнему выражению соответствует схема, изображенная на рис. 35.3. Соединенное последовательно с Z1 сопротивление ZBH называется вносимым (из вторичной цепи трансформатора в первичную).

Как следует из формулы, оно равно:

Его активная и реактивная составляющие соответственно равны:

Появление в первичном контуре активного сопротивления, вносимого из первичного контура, физически означает следующее. Энергия, подводимая к трансформатору, потребляется не только сопротивлением R1, но и сопротивлениями вторичной цепи R2 и RH, куда она передается через переменное магнитное поле между обмотками.

Из-за минуса в формуле вносимого реактивного сопротивления общее реактивное сопротивление всей цепи, равное сумме X1 и XBH, оказывается меньше индуктивного сопротивления первичной обмотки.

Это хорошо согласуется со сказанным ранее. При встречном соединении обмоток трансформатора поток Ф2, направленный противоположно потоку Ф1, уменьшает последний, что приводит к уменьшению общего индуктивного сопротивления.

Видео:Лекция 117. Правила КирхгофаСкачать

Правила (законы) Кирхгофа простыми словами

На практике часто встречаются задачи по расчётам параметров токов и напряжений в различных разветвлённых цепях. В качестве инструмента для расчётов используют правила Кирхгофа (в некоторой литературе их называют еще законами, хотя это не совсем корректно) – одни из фундаментальных правил, которые совместно с законами Ома позволяет определять параметры независимых контуров в самых сложных цепях.

Учёный Густав Киргхоф сформулировал два правила [1], для понимания которых введено понятие узла, ветви, контура. В нашей ситуации ветвью будем называть участок, по которому протекает один и тот же ток. Точки соединения ветвей образуют узлы. Ветви вместе с узлами образуют контуры – замкнутые пути, по которым течёт ток.

Видео:Как составить уравнения по законам Кирхгофа?Скачать

Первое правило Кирхгофа

Первое правило Густава Кирхгофа сформулировано исходя из закона сохранения заряда. Физик понимал, что заряд не может задерживаться в узле, а распределяется по ветвям контура, образующим это соединение.

Кирхгоф предположил, а впоследствии обосновал на основании экспериментов, что количество зарядов зашедших в узел такое же, как и количество тока вытекающего из него.

На рисунке 1 изображена простая схема, состоящая из контуров. Точками A, B, C, D обозначены узлы контура в центре схемы.

Рис. 1. Схема контура

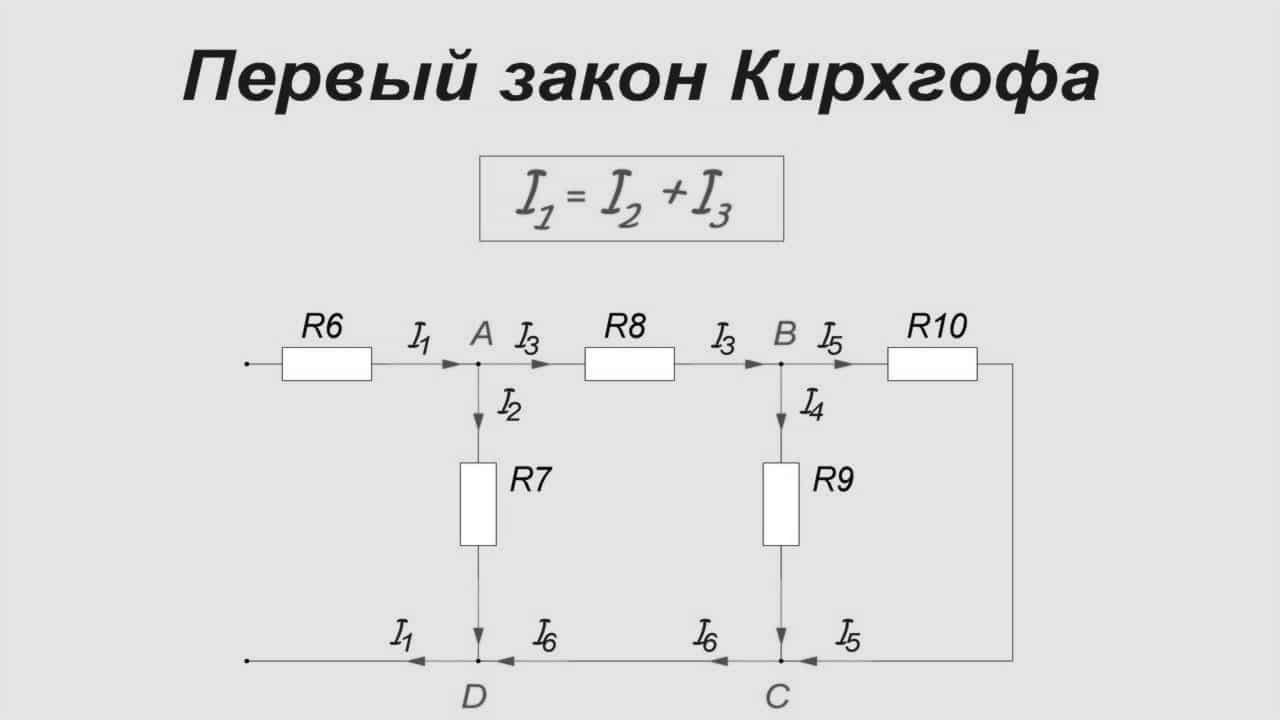
Ток I₁ входит в узел A, образованный ветвями контура. На схеме электрический заряд распределяется в двух направлениях – по ветвям AB и AD. Согласно правилу Кирхгофа, входящий ток равен сумме выходящих: I₁ = I₂ + I₃.

На рисунке 2 представлен абстрактный узел, по ветвям которого течёт ток в разных направлениях. Если сложить векторы i₁, i₂, i₃, i₄ то, согласно первому правилу Кирхгофа, векторная сумма будет равняться 0: i₁ + i₂ + i₃ + i₄ = 0. Ветвей может быть сколько угодно много, но равенство всегда будет справедливым, с учётом направления векторов.

Запишем наши выводы в алгебраической форме, для общего случая:

Для использования этой формулы, требуется учитывать знаки. Для этого необходимо выбрать направление одного из векторов тока (не важно, какого) и обозначить его знаком «плюс». При этом знаки всех других величин определить, исходя от их направления, по отношению к выбранному вектору.

Чтобы избежать путаницы, ток, направленный в точку узла, принято считать положительным, а векторы, направленные от узла – отрицательными.

Изложим первое правило Кирхгофа, выраженное приведённой выше формулой: «Алгебраическая сумма сходящихся в определённом узле токов, равна нулю, если считать входящие токи положительными, а отходящими – отрицательными».

Первое правило дополняет второе правило, сформулированное Кирхгофом. Перейдём к его рассмотрению.

Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Второе правило Киргхофа

Из третьего уравнения Максвелла вытекает правило Кирхгофа для напряжений. Его ещё называют вторым законом.

Это правило гласит, что в замкнутом контуре, на резистивных элементах, алгебраическая сумма напряжений (включая внутренние), равна сумме ЭДС, присутствующих в этом же замкнутом контуре.

При этом токи и ЭДС, векторы которых совпадают с направлением (выбирается произвольно) обхода контура, считаются положительными, а встречные к обходу токи – отрицательными.

Рис. 4. Иллюстрация второго правила Кирхгофа

Формулы, которые изображены на рисунке применяются в частных случаях для вычисления параметров простых схем.

Формулировки уравнений общего характера:

, где где L_k и C_k – это индуктивности и ёмкости, соответственно.

Линейные уравнения справедливы как для линейных, так и для нелинейных линеаризованных цепей. Они применяются при любом характере временных изменений токов и напряжений, для разных источников ЭДС. При этом законы Кирхгофа справедливы и для магнитных цепей. Это позволяет выполнять вычисления для поиска соответствующие параметров.

Видео:Урок 265. Задачи на правила КирхгофаСкачать

Закон Кирхгофа для магнитной цепи

Применение независимых уравнений возможно и при расчётах магнитных цепей. Сформулированные выше правила Кирхгофа справедливы и для вычисления параметров магнитных потоков и намагничивающих сил.

То есть, для магнитных потоков первое правило Кирхгофа можно выразить словами: «Алгебраическая сумма всевозможных магнитных потоков относительно узла магнитной цепи равняется нулю.

Сформулируем второе правило для намагничивающих сил F: «В замкнутом магнитном контуре алгебраическая сумма намагничивающих сил приравнивается к сумме магнитных напряжений». Данное утверждение выражается формулой: ∑F=∑U или ∑Iω = ∑НL, где ω – количество витков, H – напряжённость магнитного поля, символ L обозначает длину средней линии магнитопровода. ( Условно принимается, что каждая точка этой линии совпадает с линиями магнитной индукции).

Второе правило, применяемое для вычисления магнитных цепей, есть не что иное, как альтернативная форма представления закона полного тока.

Примечание: Составляя уравнения с использованием формул, вытекающих из правил Кирхгофа, надо прежде определиться с положительным направлением потоков, функционирующих в ветвях, сопоставив их с направлением обходов существующих контуров.

При совпадении векторов магнитного потока с направлениями обхода (на некоторых участках), падение напряжения на этих ветвях берём со знаком « + », а встречные ему – со знаком « – ».

Видео:Решение задачи. Расчет электрической цепи по законам КирхгофаСкачать

Примеры расчета цепей

Рассмотрим ещё раз рисунок 3. На нём изображено 4 разнонаправленных вектора: i₁, i₂, i₃, i₄. Из них – два входящие ( i₂, i₃) и два исходящие из узла (i₁, i₄). Положительными будем считать те векторы, которые направлены в точку соединения ветвей, а остальные – отрицательными.

Тогда, по формуле Кирхгофа, составим уравнение и запишем его в следующем виде: – i₁ + i₂ + i₃ – i₄ = 0.

На практике такие узлы являются частью контуров, обходя которые можно составить ещё несколько линейных уравнений с этими же неизвестными. Количество уравнений всегда достаточно для решения задачи.

Рассмотрим алгоритм решения на примере рис. 5.

Рис. 5. Пример для расчёта

Схема содержит 3 ветви и два узла, которые образуют три пары по два независимых контура:

Запишем независимое уравнение, выполняющееся, например, в точке а. Из первого правила Кирхгофа вытекает: I₁ + I₂ – I₃ = 0.

Воспользуемся вторым правилом Кирхгофа. Для составления уравнений можно выбрать любой из контуров, но нам необходимы контуры с узлом а, так как для него мы уже составили уравнение. Это будут контуры 1 и 2.

Пишем уравнения:

Решаем систему уравнений:

Так как значения R и E известны (см. рисунок 5), мы придём к системе уравнений:

Решая эту систему, получим:

Потенциал узла а равен: U_a = I₃*R₃ = 3,55 × 3 = 10,65 В. Чтобы убедиться в верности наших расчётов, проверим выполнение второго правила по отношению к контуру 3:

E₁ – E₂ + I₁R₁+ I₂R₂ = 12 – 15 + 1,36 – 4,38 = – 0,02 ≈ 0 (с учётом погрешностей, связанных с округлениями чисел при вычислениях).

Если проверка выполнения второго правила успешно завершена, то расчёты сделаны правильно, а полученные данные являются достоверными.

Применяя правила (законы) Кирхгофа можно вычислять параметры электрической энергии для магнитных цепей.

Видео:Законы Кирхгофа - самое простое и понятное объяснение этих законовСкачать

Правила Кирхгофа для электрической цепи, понятным языком

Видео:Законы Кирхгофа. Метод контурных уравненийСкачать

Формулировка правил

Сразу необходимо внести ясность. Хотя во многих технических текстах используется слово закон, на самом деле это правило. В чем различие? Закон основывается на фундаментальных истинах, фактах, правило несет более абстрактное понимание. Чтобы это лучше понять рассмотрим основы этого метода.

Из-за сложности вычислений его лучше использовать там, где схема имеет узлы и контуры. Узлом называется место соединения более двух цепей. Это как если взять три и более обычных нитки и связать их вместе. Контуром называется замкнутая цепь, включающая в себя три и более таких узла.

Отдельная ветвь может содержать сколько угодно резисторов, под которыми подразумеваются нагрузки с активным сопротивлением. Все они объединяются в один общий резистор, так как это упрощает решение задачи. Также в цепи может быть один или несколько источников питания, которые также объединяются в один элемент, либо их может и не быть. Тогда цепь будет состоять только из сопротивления.

Контур всегда начинается и заканчивается одним и тем же узлом. Поскольку узлы обозначаются латинскими или русскими буквами, то в уравнении будет на одну букву больше, чем самих соединений. Например, участок состоит из узлов A, B, C, D. Тогда обозначение этой петли будет следующим: A, B, C, D, A. На самом деле, начинать отсчет можно с любой буквы петли, например, C, D, A, B, C, просто в первом варианте легче будет не запутаться.

Определения

Как уже было сказано ветвь – это отрезок электрической цепи, в которой направление движения заряда происходит в одну сторону. Сходящиеся в узле ветви имеют разное направление токов. Контур может состоять из нескольких внутренних контуров, ветви и узлы которых также относятся к этому контуру. Сам закон Кирхгофа по существу содержит два правила, относящиеся к узлу и контуру. Самым главным и сложным является составление уравнений, учитывающих все составляющие этой формулы.

Первый закон

Первое правило говорит о сохранении заряда. Согласно ему, в узле напряжение должно быть равно нулю. Это возможно только в том случае, если все входящие токи в эту точку заходят через одни ветви, а выходят через другие. Соотношение входящих и выходящих токов может быть разным, но суммарная составляющая положительных и отрицательных потенциалов всегда одинакова.

Предположим, в узел входят токи по трем ветвям, а выходят по двум. Суммарная величина входящих токов будет точно равняться суммарной величине выходящих. Если отобразить это математически, то сумма положительных векторов I1, I2 и I3 будет равняться сумме отрицательных векторов I4 и I5.

Второй закон

Это правило связано с сохранением энергии в контуре. Другими словами, энергия источников э. д. с, входящих в контур или рассматриваемый участок, равна падению напряжения на сопротивлениях этого участка. Если выбранный участок не имеет источников питания, то суммарное падение напряжения на всех нагрузках будет равно нулю. Прежде чем переходить к расчетам, следует ознакомиться еще с некоторыми моментами.

Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Первый закон Кирхгофа

Первый закон Кирхгофа гласит, что в ветвях образующих узел электрической цепи алгебраическая сумма токов равна нулю(токи входящие в узел считаются положительными, выходящие из узла отрицательными).

Пользуясь этим законом для узла A (рисунок 1) можно записать следующее выражение:

Рисунок 1 — Первый закон Кирхгофа

I1 + I2 − I3 + I4 − I5 − I6 = 0.

Попытайтесь самостоятельно применить первый закон Кирхгофа для определения тока в ветви. На приведенной выше схеме изображены шесть ветвей образующие электрический узел В, токи ветвях входят и выходят из узла. Один из токов i неизвестен.

Запишите выражение для узла В

I1 + I2 + I3 + I4 + I5 − i = 0 I1 – I2 + I3 − I4 + I5 − i = 0 I1 + I2 + I3 − I4 + I5 − i = 0

Видео:Правила Кирхгофа - определение токов. ЭлектротехникаСкачать

Второй закон Кирхгофа.

Второй закон Кирхгофа:в контуре электрической цепи алгебраическая сумма эдс равна алгебраической сумме падений напряжения на всех сопротивлениях данного контура.

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.

Применение второго закона Кирхгофа

Для контура ABСDE, изображенного на рисунке 4, стрелками указаны положительные направления токов (произвольно). Составим уравнение согласно второму закону Кирхгофа. Для этого произвольно зададимся направлением обхода контура по часовой или против часовой стрелки. В данном примере направление обхода контура выберем по часовой стрелке.

Рисунок 4

При составлении уравнений по второму закону Кирхгофа, ЭДС записывается со знаком “+”, если ее направление совпадает с направлением произвольно выбранного обхода контура. В противном случае ЭДС записывается со знаком “-”.

Падения напряжения записываются со знаком “+”, если направление тока в нем совпадает с направлением обхода.

Начнём с эдс E1, так как её направление совпадает с обходом контура — записываем её со знаком “+” перед знаком равно.

Контур ABСDE E1 =

E2 направленна против обхода контура записываем со знаком “-” перед знаком равно.

Контур ABСDE E1 − E2=

Так как больше ЭДС в контуре ABСDЕ нет — левая часть уравнения готова.

В правой части уравнения указываются падения напряжения контура, так как направления токов I1 и I2 совпадает с обходом контура – записываем падения напряжения со знаком “+”.

Контур ABСDЕE E1 − E2 = I1*R1 + I2*R2

Направление тока I3 не совпадет с обходом контура:

Контур ABСDE E1 − E2 = I1*R1 + I2*R2 − I3*R3.

Уравнение для контура готово.

Законы Кирхгофа являются основой для расчета электрической цепи, вот несколько методов применяющие данные законы.

Видео:Применение законов Кирхгофа при решении задачСкачать

Расчеты электрических цепей с помощью законов Кирхгофа

Частота вращения: формула

Для выполнения подобных расчётов электрических цепей существует определённый алгоритм, при котором вычисляются токи для каждой ветви и напряжения на выводах всех элементов, включённых в ЭЦ. Для того чтобы рассчитать любую схему, придерживаются следующего порядка:

1. Разбивают ЭЦ на ветви, контуры и узлы.
2. Стрелками намечают предполагаемые направления движения I в ветвях. Произвольно намечают направление, по которому при написании уравнений обходят контур.
3. Пишут уравнения, применяя первое и второе правило Кирхгофа. При этом учитывают правила знаков, а именно:

• «плюс» имеют токи, втекающие в узел, «минус» – токи, вытекающие из узла;
• Е (ЭДС) и снижение напряжения на резисторах (R*I) обозначают знаком «плюс», если ток и обход совпадают по направлению, или «минус», если нет.

1. Решая полученные уравнения, находят нужные величины токов и падения напряжений на резистивных элементах.

Информация. Независимыми узлами называют такие, которые отличаются от других как минимум одной новой веткой. Ветви, содержащие ЭДС именуют активными, без ЭДС – пассивными.

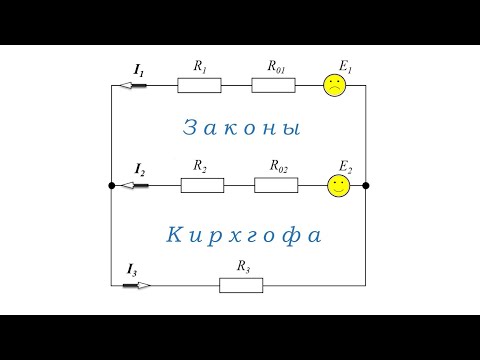
В качестве примера можно рассмотреть схему с двумя ЭДС и рассчитать токи.

Пример схемы для расчёта с двумя E

Произвольно выбирают направление токов и контурного обхода.

Намеченные направления на схеме

Составляются следующие уравнения с применением первого и второго закона Кирхгофа:

• I1 – I3 – I4 = 0 – для узла a;
• I2 + I4 – I5 = 0 – для узла b;
• R1*I1 + R3*I3 = E1 – контур acef;
• R4*I4 — R2*I2 – R3*I3 = — E2 – контур abc;
• R6*I5 + R5*I5 + R2*I2 = E2 – контур bdc.

Уравнения решаются с помощью методов определителей или подстановки.

Видео:Лекция по электротехнике 2.5 - Составление уравнений КирхгофаСкачать

Особенности составления уравнений для расчёта токов и напряжений

В первую очередь выбирается участок, который необходимо исследовать. Затем на каждой ветке произвольно устанавливается стрелка показывающая направление движения тока. Это нужно для того, чтобы потом не ошибиться. При расчете неточность направления будет исправлена. Каждую стрелку обозначают буквой I с индексом. Удобнее будет рассматривать участок, если стрелки находятся в непосредственной близости от точки соединения цепей. Источники питания и резисторы тоже обозначают, а у общего резистора добавляют сопротивление.

Внутри участка также произвольно показывают направление обхода, ориентируясь на возможные потенциалы. Оно необходимо для сравнения направления движения тока. Это сравнение покажет, какой знак должен стоять у числа. Если оба направления совпадают, ставят знак + и знак – если направления противоположны.

Число поставленных задач должно соответствовать количеству выбранных неизвестных. Допустим, имеется три цепи и необходимо вычислить их токи, значит, составленных формул также должно быть три. Получается, что в новом уравнении должен быть хотя бы один новый элемент, которого нет в предыдущих задачах.

Видео:решение задачи составлением уравнений по правилам киргофа. Законы киргофа кратко на практикеСкачать

Значение для электротехники

Правила Кирхгофа являются дополнением к другим законам. Основная сложность состоит в нахождении участков, поскольку их границы не всегда легко обнаружить. После ограничения нужной области необходимо выделить все неизвестные. Составление задач уже относительно легкое дело. Решаются они как обычные уравнения.

Поэтому, несмотря на первые трудности, эти правила все же легче составить и решить, чем использовать, допустим, закон Ома. Поэтому они широко используются в электротехнике. Чтобы понять, как на практике применить описанный способ, рассмотрим один пример.

Видео:Метод узловых и контурных уравненийСкачать

Значение в математике

Имеется контур, состоящий из четырех цепей. В первой содержится источник питания ε1 с внутренним сопротивлением источника r1, во второй какая-то нагрузка R1. Третья имеет источник питания и нагрузку. Четвертая состоит из нагрузки. Точки B и F являются узлами. Стрелки возле них показывают предположительное направление тока. Стрелка внутри участка показывает направление обхода. Необходимо найти ток в цепях: AK, AB, BF, CD. По идее нужно составить четыре уравнения, но поскольку ε1 и R1 единственные на участке KAB, то их объединим в одну цепь. Выходит, нужно составить три уравнения.

Первое берется из первого правила: I1 + I2 + I3 = 0. Поскольку I1, I2 втекают в узел B, они имеют положительный знак, а I3 вытекает из него, то имеет отрицательный знак. Подставляем в уравнение и получаем I1 + I2 – I3 = 0, или в таком виде I1 + I2 = I3. Второе и третье уравнение берем из второго правила. Для этого используем контур BCDFB и преобразуем формулировку в математическое решение: ε2 = I2 × R2 + I3 × R3. Для участка ACDKA получаем соответственно ε1 = I1 × R1 + I3 × R3. Для наглядности вынесем их отдельно.

ε1 = I1 × R1 + I3 × R3

ε2 = I2 × R2 + I3 × R3

Получилось три задачи. Определимся с номиналами. Первый источник питания равен 6 В, второй – 12 В. Хотя так поступать нельзя, потому что параллельные источники питания должны быть одинаковыми, но нам это пригодится для получения важного урока. Первое сопротивление равно 2 Ом, второе – 4 Ом, третье – 8 Ом.

Осталось вставить данные в уравнения и получаем: для второго номера 6 = 2I1 + 8I3, для третьего номера 12 = 4I2 + 8I3. Дальше избавляемся от общего неизвестного I3. Согласно первому пункту, он равен I1 + I2. Подставляем вместо него эту сумму и получаем: 6 = 2I1 + 8(I1 + I2), 12 = 4I2 + 8(I1 + I2). Раскрываем скобки и складываем одинаковые неизвестные: 6 = 10I1 + 8I2; 12 = 12I2 + 8I1. Чтобы найти I1, нужно избавиться от I2. Для этого первое уравнение умножаем на 12, а второе на 8 и получаем: 72 = 120I1 + 96I2; 96 = 96I2 + 64I1. От первого отнимаем второе и записываем остаток -24 = 56I1, или I1 = -24/56 = -6/14 А. Почему ток отрицательный?

Потому что источники питания разные. На втором источнике напряжение выше, чем на первом, поэтому ток идет в обратном направлении. Находим I2, для этого значение I1 вставляем в любое из последних уравнений: 96 = 96I2 – 64 24/56. Разделим левую и правую часть на 96 и получим: 1 = I2 – (64×24)/(96×56) или дробную часть переносим влево, меняя знак. I2 = 1(64×24)/(96×56), после всех сокращений получаем 1 4/14 А. Для нахождения I3 воспользуемся первым номером: I3 = I1 + I2. I3 = -24/56 + 1 4/14 = 1(4×56)/(14×56) – (24×14)/(56×14) = 1 224/784 -336/784 = 1008/784 -336/784 = 672/774 ≈ 0,87А. Получили I1 = -6/14 А, I2 = 1 4/14 А, I3 ≈ 0,87А.

Видео:Урок 14. Законы Кирхгофа простыми словами с примерамиСкачать

Закон Кирхгофа в химии

Когда в ходе химреакции система меняет свою теплоёмкость, вместе с тем меняется и температурный коэффициент возникающего в результате этого процесса теплового эффекта. Применяя уравнение, вытекающее из этого закона, можно рассчитывать тепловые эффекты в любом диапазоне температур. Дифференциальная форма этого уравнения имеет вид:

• ∆Cp – температурный коэффициент;
• d∆Q – изменение теплового эффекта;
• dT – изменение температуры.

Важно! Коэффициент определяет, как изменится тепловой эффект при изменении температуры на 1 К (2730С).

Теорема Кирхгофа для термодинамики

Третье уравнения Максвелла, а также принцип сохранения зарядов позволили Густаву Кирхгофу создать два правила, которые применяются в электротехнике. Имея данные о значениях сопротивлений резисторов и ЭДС источников питания, можно рассчитывать протекающий I или приложенное U для любого элемента цепи.

Видео:МКТ │Цепь с источниками тока │Расчет цепи методом контурных токовСкачать

Алгебраическая сумма разностей потенциалов

Закон напряжения по Густаву Кирхгофу — второй закон этого автора, используемый для анализа электрической схемы. Вторым законом Кирхгофа утверждается, что для последовательного замкнутого контура алгебраическая сумма всех напряжений по кругу любой замкнутой цепи равна нулю. Утверждение обусловлено тем, что контур цепи является замкнутым проводящим путём, где потери энергии исключаются. Другими словами, алгебраическая сумма разностей потенциалов замкнутого контура теоретически равняется нулю:

Следует обратить внимание: под термином «алгебраическая сумма» имеется в виду учёт полярностей и признаков источников ЭДС, а также падения напряжений по кругу контура. Эта концепция закона Кирхгофа, известная как «сохранение энергии», как движение по кругу замкнутого контура или схемы, утверждает логику возврата к началу цепи и к первоначальному потенциалу без потери напряжения по всему контуру.

Следовательно, любое падение напряжения по кругу контура теоретически равно потенциалу любых источников напряжения, встречающихся на этом пути.

Отсюда следует вывод: применяя Второй закон Кирхгофа к определенному элементу электрической схемы, важно обращать особое внимание на алгебраические знаки падений напряжения на элементах (источниках ЭДС), иначе вычисления оборачиваются ошибкой.

Одиночный контурный элемент — резистор

Простым примером с резистором предположим — ток протекает в том же направлении, что и поток положительного заряда. В этом случае поток тока через резистор протекает от точки A до точки B. Фактически — от положительной клеммы до отрицательной клеммы. Таким образом, поскольку движение положительного заряда отмечается в направлении аналогичном направлению течения тока, на резистивном элементе зафиксируется падение потенциала, которое приведет к падению минусового потенциала на резисторе (— I * R).

Если же поток тока от точки B до точки A протекает в противоположном направлении относительно потока положительного заряда, тогда через резистивный элемент отметится рост потенциала, поскольку имеет место переход от минусового потенциала к потенциалу плюсовому, что даёт падение напряжения (+ I * R). Таким образом, чтобы правильно применить закон Кирхгофа по напряжению к электрической цепи, необходимо точно определить направление полярности. Очевидно, знак падения напряжения на резисторе зависит от направления тока, протекающего через резистор.

Направление потока тока по замкнутому контуру допустимо определять либо по часовой стрелке, либо против часовой стрелки, и любой вариант допустим к выбору. Если выбранное направление отличается от фактического направления тока, соответствие закону Кирхгофа получится корректным и действительным, но приведет к результату, когда алгебраический расчёт будет иметь знак минус. Чтобы лучше понять эту концепцию, логично рассмотреть ещё один пример с одним контуром цепи на соответствие Второму Закону Кирхгофа.

Одиночный контур электрической цепи

Второй закон Кирхгофа утверждает — алгебраическая сумма разностей потенциалов любого замкнутого контура равна нулю. Демонстрационная схема действия Второго закона Кирхгофа для замкнутого контура с двумя резисторами и одним источником ЭДС. Если принять условие, что два резистора R1 и R2 соединены последовательно, оба элемента являются частью одного контура. Соответственно, одинаковый ток протекает через каждый из резисторов.

Таким образом, падение напряжения на резисторе R1 = I * R1 и падение напряжения на резисторе R2 = I * R2, дают напряжение по Второму закону Кирхгофа:

Очевидно: применение Второго закона Кирхгофа к одиночному замкнутому контуру даёт формулу эквивалентного или полного сопротивления для последовательной цепи. Допустимо расширить эту формулу, чтобы найти значения падений потенциалов по кругу контура:

Vr1 = V * (R1 / R1 + R2)

Vr2 = V * (R2 / R1 + R2)

Есть три резистора номинальным сопротивлением 10, 20, 30 Ом, соответственно. Все три резистивных элемента соединены последовательно к 12-вольтовому аккумулятору.

Интересно по теме: Как проверить стабилитрон.

• общее сопротивление,
• ток цепи,
• ток через каждый резистор,
• падение напряжения на каждом резисторе.

Рассчитаем общее сопротивление:

Ro = R1 + R2 + R3 = 10Ω + 20Ω + 30Ω = 60Ω

I = V / Ro = 12 / 60 = 0,2A (200 мА)

Ток через каждый резистор:

I * R1 = I * R2 = I * R3 = 0,2A (200 мА)

Падение потенциала на каждом из резисторов:

VR1 = I * R1 = 0.2 * 10 = 2В

VR2 = I * R2 = 0.2 * 20 = 4В

VR3 = I * R3 = 0.2 * 30 = 6В

Таким образом, Второй закон Кирхгофа справедлив, учитывая что индивидуальные падения напряжения, отмеченные по кругу замкнутого контура, в итоге составляют сумму напряжений.

Видео:Лекция по темам: "Узел, ветвь и контур . Последовательное и параллельное соединение резисторов"Скачать

Что такое правило напряжений Кирхгофа (второй закон Кирхгофа)?

Принцип, известный как правило напряжений Кирхгофа (открытое в 1847 году немецким физиком Густавом Р. Кирхгофом), можно сформулировать следующим образом:

«Алгебраическая сумма всех напряжений в замкнутом контуре равна нулю»

Под алгебраической я подразумеваю, помимо учета величин, учет и знаков (полярностей). Под контуром я подразумеваю любой путь, прослеживаемый от одной точки в цепи до других точек в этой цепи, и, наконец, обратно в исходную точку.

Видео:Урок 263. Правила КирхгофаСкачать

Демонстрация закона напряжений Кирхгофа в последовательной цепи

Давайте еще раз посмотрим на наш пример последовательной схемы, на этот раз нумеруя точки цепи для обозначения напряжений:

Рисунок 1 – Демонстрация закона напряжений Кирхгофа в последовательной цепи

Если бы мы подключили вольтметр между точками 2 и 1, красный измерительный провод к точке 2 и черный измерительный провод к точке 1, вольтметр зарегистрировал бы значение +45 вольт. Для положительных показаний на дисплеях цифровых счетчиков знак «+» обычно не отображается, а скорее подразумевается. Однако для этого урока полярность показаний напряжений очень важна, поэтому я буду явно показывать положительные числа:

Когда напряжение указывается с двойным нижним индексом (символы «2-1» в обозначении «E2-1»), это означает напряжение в первой точке (2), измеренное по отношению ко второй точке (1). Напряжение, указанное как «Ecd», будет означать значение напряжения, показанное цифровым мультиметром с красным измерительным проводом в точке «c» и черным измерительным проводом в точке «d»: напряжение в точке «c» относительно точки «d».

Рисунок 2 – Значение Ecd

Если бы мы взяли тот же вольтметр и измерили падение напряжения на каждом резисторе, обходя цепь по часовой стрелке с красным измерительным проводом нашего мультиметра на точке впереди и черным измерительным проводом на точке позади, мы получили бы следующие показания:

Рисунок 3 – Определение напряжений в последовательной цепи

Нам уже должен быть знаком общий для последовательных цепей принцип, утверждающий, что отдельные падения напряжения в сумме составляют общее приложенное напряжение, но измерение падения напряжения таким образом и уделение внимания полярности (математическому знаку) показаний открывает еще один аспект этого принципа: все измеренные напряжения в сумме равны нулю:

В приведенном выше примере контур образован следующими точками в следующем порядке: 1-2-3-4-1. Не имеет значения, с какой точки мы начинаем или в каком направлении движемся при следовании по контуру; сумма напряжений по-прежнему будет равна нулю. Чтобы продемонстрировать это, мы можем той же цепи подсчитать напряжения в контуре 3-2-1-4-3:

Этот пример может быть более понятен, если мы перерисуем нашу последовательную схему так, чтобы все компоненты были представлены на одной прямой линии:

Рисунок 4 – Изменение представления последовательной цепи

Это всё та же последовательная схема, только с немного перераспределенными компонентами. Обратите внимание на полярность падений напряжения на резисторах по отношению к напряжению батареи: напряжение батареи отрицательное слева и положительное справа, тогда как все падения напряжения на резисторах ориентированы в другую сторону (положительное слева и отрицательное справа). Это потому, что резисторы сопротивляются потоку электрического заряда, проталкиваемого батареей. Другими словами, «толкание», прилагаемое резисторами против потока электрического заряда, должно происходить в направлении, противоположном источнику электродвижущей силы.

Здесь мы видим, что цифровой вольтметр покажет на каждом компоненте в этой цепи, если черный провод будет слева, а красный провод – справа:

Рисунок 5 – Измерение напряжений в последовательной цепи

Если бы мы взяли тот же вольтметр и измерили напряжение между комбинациями компонентов, начиная с единственного R1 слева и продвигаясь по всей цепочке компонентов, мы увидели бы, как напряжения складываются алгебраически (до нуля):

Рисунок 6 – Измерение суммы напряжений в последовательной цепи

Тот факт, что последовательные напряжения складываются, не должен быть тайной, но мы заметили, что полярность этих напряжений имеет большое значение в том, как эти значения складываются. При измерении напряжения на R1 – R2 и R1 – R2 – R3 (я использую символ «двойное тире» «–» для обозначения последовательного соединения между резисторами R1, R2 и R3), мы видим, как измеряются бо́льшие значения напряжений (хотя и отрицательные), потому что полярности отдельных падений напряжения имеют одинаковую ориентацию (плюс слева, минус справа).

Сумма падений напряжения на R1, R2 и R3 равна 45 вольт, что соответствует выходному напряжению батареи, за исключением того, что полярность напряжения батареи (минус слева, плюс справа) противоположна падениям напряжения на резисторах, поэтому при измерении напряжения на всей цепочке компонентов мы получаем 0 вольт.

То, что мы должны получить ровно 0 вольт на всей линии, тоже не должно быть тайной. Глядя на схему, мы видим, что крайняя левая часть линии (левая сторона R1, точка номер 2) напрямую соединена с крайней правой частью линии (правая сторона батареи, точка номер 2), что необходимо для завершения схемы.

Поскольку эти две точки соединены напрямую, они являются электрически общими друг с другом. Таким образом, напряжение между этими двумя электрически общими точками должно быть равно нулю.

Видео:Законы которые невозможно нарушить: Законы Кирхгофа #ShortsСкачать

Демонстрация закона напряжений Кирхгофа в параллельной цепи

Правило напряжений Кирхгофа (второй закон Кирхгофа) будет работать вообще для любой конфигурации схемы, а не только для простых последовательных цепей. Обратите внимание, как это работает для следующей параллельной схемы:

Рисунок 7 – Параллельная схема из резисторов

При параллельной схеме напряжение на каждом резисторе равно напряжению питания: 6 вольт. Суммируя напряжения вдоль контура 2-3-4-5-6-7-2, мы получаем:

Обратите внимание, что конечное (суммарное) напряжение я обозначил как E2-2. Поскольку мы начали наше пошаговое прохождение по контуру в точке 2 и закончили в точке 2, алгебраическая сумма этих напряжений будет такой же, как напряжение, измеренное между той же точкой (E2-2), которое, конечно, должно быть равно нулю.

Видео:Первый закон Кирхгофа простыми словами: определение, формула и примеры использования.Скачать

Справедливость закона Кирхгофа о напряжениях независимо от топологии цепи

Тот факт, что эта цепь является параллельной, а не последовательной, не имеет ничего общего со справедливостью закона Кирхгофа о напряжениях. В этом отношении схема может быть «черным ящиком» (конфигурация ее компонентов полностью скрыта от нашего взгляда) с набором открытых клемм, между которыми мы можем измерить напряжение, – и правило напряжений Кирхгофа всё равно останется верным:

Рисунок 8 – Справедливость закона Кирхгофа напряжениях независимо от топологии схемы

Попробуйте на приведенной выше диаграмме выполнить обход в любом порядке, начиная с любого вывода, и вернувшись к исходному выводу, и вы обнаружите, что алгебраическая сумма напряжений всегда равна нулю.

Более того, «контур», который мы отслеживаем для второго закона Кирхгофа, даже не обязательно должен быть реальным путем протекания тока в прямом смысле этого слова. Всё, что нам нужно сделать, чтобы соответствовать правилу напряжений Кирхгофа, – это начинать и заканчивать в одной и той же точке цепи, подсчитывая падения напряжения и полярности при переходе между точками. Рассмотрим следующий абсурдный пример, проходя по «контуру» 2-3-6-3-2 в той же параллельной резисторной цепи:

Рисунок 9 – Параллельная схема из резисторов

Видео:Расчет цепи по законам КирхгофаСкачать

Использование закона Кирхгофа о напряжениях в сложной цепи

Закон Кирхгофа о напряжениях можно использовать для определения неизвестного напряжения в сложной цепи, где известны все другие напряжения вдоль определенного «контура». В качестве примера возьмем следующую сложную схему (на самом деле две последовательные цепи, соединенные одним проводом внизу):

Рисунок 10 – Правило напряжений Кирхгофа в сложной цепи

Чтобы упростить задачу, я опустил значения сопротивлений и просто указал падение напряжения на каждом резисторе. Две последовательные цепи имеют между собой общий провод (провод 7-8-9-10), что делает возможными измерения напряжения между этими двумя цепями. Если бы мы хотели определить напряжение между точками 4 и 3, мы могли бы составить уравнение правила напряжений Кирхгофа с напряжением между этими точками как неизвестным:

E4-3 + E9-4 + E8-9 + E3-8 = 0

E4-3 + 12 + 0 + 20 = 0

Рисунок 11 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3
Рисунок 12 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 9 и 4
Рисунок 13 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 8 и 9
Рисунок 14 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 8

Обойдя контур 3-4-9-8-3, мы записываем значения падений напряжения так, как их регистрировал бы цифровой вольтметр, измеряя с красным измерительным проводом в точке впереди и черным измерительным проводом на точке позади, когда мы продвигаемся вперед по контуру. Следовательно, напряжение в точке 9 относительно точки 4 является положительным (+) 12 вольт, потому что «красный провод» находится в точке 9, а «черный провод» – в точке 4.

Напряжение в точке 3 относительно точки 8 составляет положительные (+) 20 вольт, потому что «красный провод» находится в точке 3, а «черный провод» – в точке 8. Напряжение в точке 8 относительно точки 9, конечно, равно нулю, потому что эти две точки электрически общие.

Наш окончательный ответ для напряжения в точке 4 относительно точки 3 – это отрицательные (-) 32 вольта, говорящие нам, что точка 3 на самом деле положительна относительно точки 4, именно это цифровой вольтметр показал бы при красном проводе в точке 4 и черном проводе в точке 3:

Рисунок 15 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 4 и 3

Другими словами, первоначальное размещение наших «измерительных щупов» в этой задаче правила напряжений Кирхгофа было «обратным». Если бы мы сформировали наше уравнение второго закона Кирхгофа, начиная с E3-4, вместо E4-3, обходя тот же контур с противоположной ориентацией измерительных проводов, окончательный ответ был бы E3-4 = +32 вольта:

Рисунок 16 – Правило напряжений Кирхгофа в сложной цепи. Напряжение между точками 3 и 4

Важно понимать, что ни один из подходов не является «неправильным». В обоих случаях мы приходим к правильной оценке напряжения между двумя точками 3 и 4: точка 3 положительна по отношению к точке 4, а напряжение между ними составляет 32 вольта.