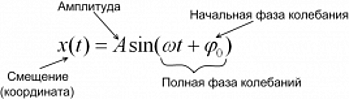Лекция 5. Механические колебания
План лекции
5.1. Основные характеристики колебательного движения.
5.2. Кинетическая, потенциальная и полная энергии гармонических колебаний.
5.3. Уравнение гармонических колебаний. Маятники.
5.4. Затухание колебания.
5.5. Вынужденные колебания. Резонанс.
5.6. Явление резонанса в строительстве.
Основные характеристики колебательного движения
Процессы точно или приблизительно повторяющиеся через одинаковые промежутки времени называются колебаниями.В зависимости от физической природы различают механические, электромагнитные и другие виды колебаний. Несмотря на разную природу колебаний, в них обнаруживаются одни и те же физические закономерности, они описываются одними и теми же математическими уравнениями и исследуются общими методами, разработка и применение которых составляют задачу теории колебаний.
В данном курсе физики мы будем изучать два наиболее распространенных класса колебаний: механические и электрические.
Среди разнообразных колебаний основную и существенную роль играют так называемые гармонические колебания, то есть такие, при которых колеблющаяся величина изменяется с течением времени по закону синуса или косинуса.
Рассмотрим гармонические колебания на примере колеблющейся точки.
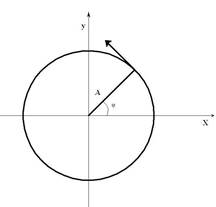
Пусть точка вращается по окружности радиуса А с угловой скоростью ω0 (рис.5.1).
Рис.5.1.
Если точку спроецировать на оси X и Y, то ее проекции будут совершать колебания и удовлетворяют следующим уравнениям соответственно
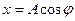
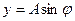
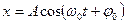
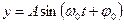
где х и y – смещения колеблющейся точки от положения равновесия;
А – амплитуда колебания (максимальное смещение);
ω0 – круговая (циклическая) частота колебаний.
Точка совершает одно полное колебание за время Τ, называемое периодом колебания. Частота колебаний ν (число колебаний в единицу времени) есть 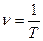
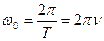
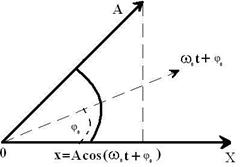
Геометрический смысл параметров уравнений (5.2) можно объяснить с помощью векторных диаграмм. Выберем на оси Х точку О и из этой точки под углом φ0 проведем вектор А. Будем вращать вектор А с угловой скоростью ω0 и тогда его проекция на ось будет смещаться на величину x (рис. 5.2).
Рис.5.2.
Колеблющаяся точка обладает скоростью и ускорением. Скорость материальной точки
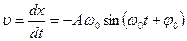
Ускорение материальной точки
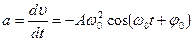
С учетом формулы (5.2) получим
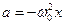
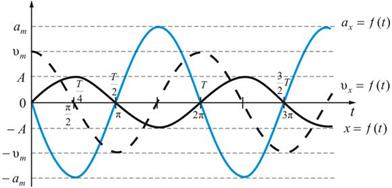
Сравнивая уравнения (5.2), (5.4) и (5.5) замечаем, что скорость опережает смещение на π/2. Фазы ускорения и смещения различаются на π (изменяются в противофазе). Графические зависимости смещения, скорости и ускорения от времени показаны на рис.5.3.
Умножив обе части равенства уравнения (5.6) на массу m материальной точки получим
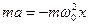
Используя II закон Ньютона, получаем
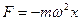
Рис.5.3.
Таким образом, чтобы совершались гармонические колебания на материальную точку должна действовать сила F, пропорциональная смещению x, которая возвращает ее в положение равновесия
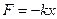
где, k – некоторый коэффициент (зависящий от свойств колеблющейся системы) и называемой жесткостью.
Из уравнения (5.7) и (5.8) видно, что 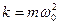
Кинетическая, потенциальная и полная энергии гармонических колебаний
Полная энергия Е колеблющейся материальной точки равна сумме кинетической Ек и потенциальной Еп энергий
Кинетическую энергию можно найти, зная массу m и скорость u
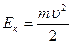
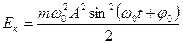
Выражение для потенциальной энергии можно найти из соотношений между потенциальной энергией и силой.
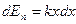
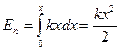
Учитывая, что 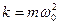
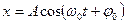
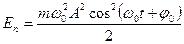
Полную энергию получим сложив (5.12) и (5.15)
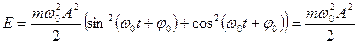
Таким образом, полная энергия пропорциональна квадрату амплитуды колебаний.
Из формул (5.12) и (5.15) видно, что когда 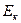
5.3. Уравнение гармонических колебаний.
Маятники
На колеблющуюся материальную точку массой m действует возвращающая сила F = — kx. Эта сила вызывает ускорение 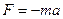
где, k – жесткость системы, 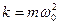
Сделав соответствующие подстановки в (5.17), получим
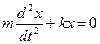
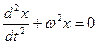
Уравнение (5.18) представляет собой дифференциальное уравнение второго порядка незатухающих гармонических колебаний материальной точки.
Решением этого дифференциального уравнения как раз и является уравнение (5.2): 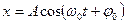
Колебания любого гармонического осциллятора (или гармонического вибратора) описываются дифференциальным уравнением второго порядка
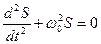
Решением этого уравнения является
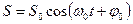
где S0 – амплитудное (максимальное) значение параметра S.
Примерами гармонических осцилляторов являются маятники, колебательный контур.
В качестве примера малых колебаний рассмотрим колебания маятников.
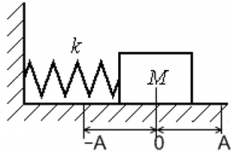
Пружинный маятник
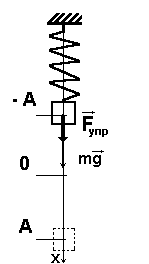
Груз массой m, подвешенный на упругой пружине представляет собой пружинный маятник (рис.5.4). Если груз оттянуть вниз и отпустить, то под действием силы F = -kx маятник будет совершать колебания; k – коэффициент жесткости (в данном случае коэффициент упругости).
Рис.5.4.
Уравнение движения маятника имеет вид
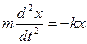
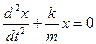
Его решением является
Это значит, что пружинный маятник совершает гармонические колебания с циклической частотой ω0
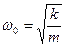
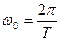
Период колебаний пружинного маятника
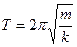
Физический маятник
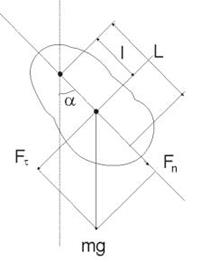
Физическим маятником называется твердое тело, которое может колебаться под действием силы тяжести вокруг оси, не проходящей через центр масс. При отклонении маятника относительно оси О угол α, на него действует М – момент возвращающей силы 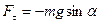
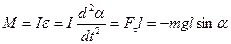
где, I – момент инерции относительно оси О;
l – плечо силы Fτ; при малых углах 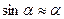
Рис.5.5.
Из (5.22) получаем дифференциальное уравнение
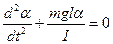
Сравнив уравнение (5.23) с уравнением гармонического осциллятора (5.19), получим
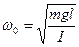
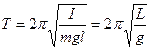
где, 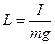
От точки подвеса О на линии ОС на расстоянии L находится точка О1, называемая центром качения. Точки О и О1 обладает свойством взаимозаменяемости.
Видео:Урок 114. Работа. Теорема о кинетической энергииСкачать

Энергия гармонических колебаний
Введём энергию колебания.
Колебательная система движется со скоростью , тогда его кинетическая энергия должна быть равна:
- где
- — кинетическая энергия системы
- — масса колеблющегося тела
- — скорость тела в данный момент
Вспомним зависимость скорости от времени при гармоническом колебании:
- где
- — амплитуда (максимальное значение) колебания
- — циклическая частота колебания
- — начальная фаза колебания
- — время от начала колебания
Подставим (2) в (1) при условии (для упрощения):
Тогда максимальная кинетическая энергия данной системы:
т.к. максимальное значение .
С другой стороны для пружинного маятника можем записать потенциальную энергию деформации:
- где
- — потенциальная энергия деформации
- — жёсткость пружины
Вспомним зависимость координаты от времени при гармоническом колебании:
Подставим (5) в (4) при условии (для упрощения):
Тогда максимальная потенциальная энергия данной системы:
т.к. максимальное значение .
Вывод: задачи школьной физики чаще всего связаны именно с максимальным значением энергии колебания. Её можно рассчитать и как кинетическую энергию в положении равновесия (4), и как потенциальную энергию в точке максимального отклонения (8).
Видео:Потенциальная и кинетическая энергияСкачать

17. Механика  Читать 0 мин.
Читать 0 мин.
Видео:Теорема о кинетической энергииСкачать

17.547. Механические колебания
Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.
Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.
Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $frac$ , где
Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $frac$ , где
N ― количество колебаний;
Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $frac$ , где
ω ― циклическая частота [рад/с];
Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:
ω ― циклическая частота [рад/с];
φ0 ― начальная фаза колебаний, [рад];
Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.
Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.
Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.
Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где
φ ― полная фаза колебаний [рад];
φ0 ― начальная фаза колебаний, [рад];
ω ― циклическая частота [рад/с];
Пример анализа гармонических колебаний точки
Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где
ω ― циклическая частота [рад/с].
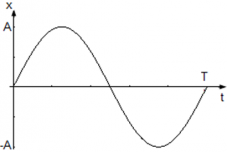
Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна φ = $frac +2pi n$ когда x = –A фаза колебаний принимает значения φ = $frac +2pi n$ , где n = 0, 1 , 2, … N.
График колебания координаты точки имеет вид:
Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где
v ― скорость движения точки [м/с];
Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).
Уравнение скорости точки равно v(t) = Acos(ωt), где
v ― скорость движения точки [м/с];
ω ― циклическая частота [рад/с];
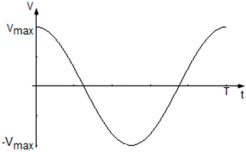
Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.
График колебания скорости точки имеет вид:
Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.
Ускорение ― это производная скорости по времени: a = vt‘, где
a ― ускорение движения точки [м/с2];
v ― скорость движения точки [м/с];
Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).
Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где
a ― ускорение движения точки [м/с2];
ω ― циклическая частота [рад/с];
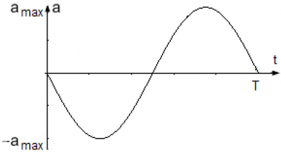
Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.
График колебания ускорения точки имеет вид:
Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где
E ― полная механическая энергия системы, E = const, [Дж];
EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];
EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].
Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).
Потенциальная энергия деформированной пружины равна EП = $frac$ , где
EП ― потенциальная энергия деформированной пружины, [Дж];
k ― коэффициент упругости пружины [Н/м];
x ― деформация пружины (величина ее удлинения или сжатия) [м].
У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $frac$ = $frac$ = $frac cdot A^2 sin^2 (omega t)$ .
Уравнение потенциальной энергии пружинного маятника EП = $frac cdot A^2 sin^2 (omega t)$ , где
EП ― потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
ω ― циклическая частота [рад/с];
Амплитуда потенциальной энергии пружинного маятника равна EПmax = $fracA^2$ , где
EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
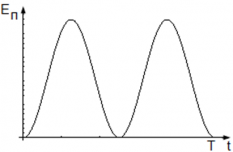
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.
График колебаний потенциальной энергии пружинного маятника:
Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $frac$ , где
Eк ― кинетическая энергия тела, [Дж];
v ― скорость движения тела, [м/с].
У тела, которое совершает колебательные движения, скорость ― переменная величина.
Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $frac$ = $frac cdot (Aomegacos(omega t))^2$ = $frac cdot A^2 omega^2 cos^2 (omega t)$ .
Уравнение кинетической энергии маятника Eк = $frac cdot A^2 omega^2 cos^2 (omega t)$ , где
Eк ― кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с];
Амплитуда кинетической энергии маятника равна EКmax = $frac cdot A^2 omega^2$ , где
EКmax ― максимальная кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с].
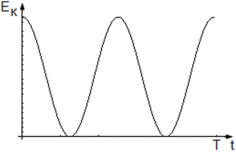
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.
График колебаний кинетической энергии маятника:
Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.
Период колебаний математического маятника равен T = $2pi sqrt<frac>$ , где
l ― длина нити математического маятника [м];
g ― ускорение свободного падения [м/с2].
Период колебаний пружинного маятника равен T = $2pi sqrt<frac>$ , где
Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.
На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.
📹 Видео
Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Теорема Кенига, кинетическая энергия тела | Олимпиадная физика, механика | 9, 10, 11 классСкачать

Энергия. Кинетическая и потенциальная энергия. 7 класс.Скачать

Превращение энергии при колебаниях. Уравнение колебательного движения. 1 часть. 9 класс.Скачать

Урок 125. Работа, мощность и кинетическая энергия при вращательном движенииСкачать

Урок 151. Средняя кинетическая энергия молекул многоатомного газаСкачать

ПОТЕНЦИАЛЬНАЯ энергия | КИНЕТИЧЕСКАЯ энергияСкачать

Задача на теорему об изменении кинетической энергииСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Кинетическая и потенциальная энергияСкачать

Потенциальная и Кинетическая🤔Скачать

Урок 333. "Энергетический" метод расчета частоты свободных колебанийСкачать

§ 2.13. Теорема об изменении кинетической энергии точкиСкачать

Урок 327. Гармонические колебанияСкачать

Теорема об изменении кинетической энергии. Авторы: Малкова Полина, Петрашова ПолинаСкачать

Урок 325. Колебательное движение и его характеристикиСкачать

Д10 теорема об изменении кинетической энергииСкачать

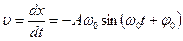
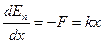
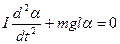
 Читать 0 мин.
Читать 0 мин.