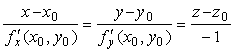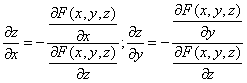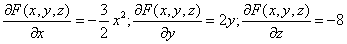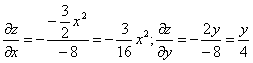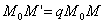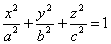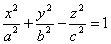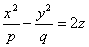Уравнение касательной плоскости к эллиптическому параболоиду (7 видео)

Содержание

Касательная плоскость и нормаль к поверхности
Примеры. 1. Найти уравнения касательной плоскости и нормали:
Уравнение касательной плоскости к эллиптическому параболоиду
Глава 46. Поверхности второго порядка
📺 Видео

Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

Касательная плоскость и нормаль к поверхности

Касательной плоскостью к поверхности σ в её точке М₀ называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М₀.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M₀(x₀,y₀,z₀) имеет вид:

Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M₀(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 0 , y₀ = 1 , тогда z₀ = 5
Найдем частные производные функции z = x^3+5*y :
f’_x(x,y) = (x 3 +5•y)’_x = 3•x 2
f’_x(x,y) = (x 3 +5•y)’_y = 5
В точке М₀(0,1) значения частных производных:
f’_x(0;1) = 0
f’_y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0

Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M₀(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:

Для нашей функции:

Тогда:

В точке М₀(1,0,1) значения частных производных:
f’_x(1;0;1) = -3 /₁₆
f’_y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀: z — 1 = -3 /₁₆(x — 1) + 0(y — 0) или 3 /₁₆•x+z- 19 /₁₆ = 0

Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М₀(x₀, y₀, z₀), принадлежащей ей, если x₀ = –1, y₀ = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
f_x’(x, y) = (y/x + xy – 5x 3 )’_x = – y/x 2 + y – 15x 2 ;
f_y’ (x, y) = (y/x + xy – 5x 3 )’_y = 1/x + x.
Точка М₀(x₀, y₀, z₀) принадлежит поверхности σ, поэтому можно вычислить z₀, подставив заданные x₀ = –1 и y₀ = 2 в уравнение поверхности:

Пример №1 . Дана функция z=f(x,y) и две точки А(х₀, y₀) и В(х₁,y₁). Требуется: 1) вычислить значение z₁ функции в точке В; 2) вычислить приближенное значение z₁ функции в точке В исходя из значения z₀ функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x₀,y₀,z₀).
Решение.
Запишем уравнения касательной в общем виде:
z — z₀ = f’_x(x₀,y₀,z₀)(x — x₀) + f’_y(x₀,y₀,z₀)(y — y₀)
По условию задачи x₀ = 1, y₀ = 2, тогда z₀ = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_x = 2•x+3•y 3
f’_x(x,y) = (x 2 +3•x•y•+y 2 )’_y = 9•x•y 2
В точке М₀(1,2) значения частных производных:
f’_x(1;2) = 26
f’_y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М₀:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0

Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Примеры. 1. Найти уравнения касательной плоскости и нормали:

1. Найти уравнения касательной плоскости и нормали:

а) к поверхности в точке М(1, 1, 1).

Находим частные производные и их значения в указанной точке касания:

На основе формул (1) и (2) составим уравнения касательной и нормали.

Уравнение касательной плоскости:

б) к эллиптическому параболоиду в точке .

Преобразуем уравнение поверхности к виду: .

И, обозначив его левую часть через , найдем частные производные:

, , .

Вычислим их числовые значения в указанной точке :

, , .

Подставляя найденные значения в общие уравнения (3) и (4), получим

— уравнение касательной плоскости:

— уравнение нормали к поверхности в этой точке:

2. На сфере найти точки, где касательная параллельна плоскости .

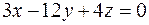
1) Пользуясь общим уравнением (3), составим уравнение касательной плоскости к данной сфере в ее точке (координаты которой нам нужно найти):

, , — частные производные уравнения сферы.

, , — их значения в точке касания. Отсюда:

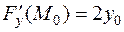
Сократив выражение на 2, и раскрыв скобки, получим:

или .

2) Точка сферы должна удовлетворять ее уравнению . Это означает, что . Следовательно,

3) Воспользуемся условием параллельности искомой касательной к заданной плоскости. Согласно условию параллельности двух плоскостей, коэффициенты при текущих координатах этих плоскостей должны быть пропорциональны:

Запишем последние равенства в виде системы уравнений:

(*)

4) Подставим найденные в параметрическом виде (*) координаты точек сферы в ее уравнение:

откуда находим, что .

5) Подставляя найденные числовые значения в (*), найдем координаты искомых точек, в которых касательная плоскость параллельна заданной плоскости:

и .

3. Показать, что касательные плоскости к поверхности образуют с координатными плоскостями тетраэдр постоянного объема.

Уравнение касательной плоскости к данной поверхности в точке имеет вид:

Эта плоскость на координатных осях отсекает отрезки:

, , .

Перечисленные отрезки являются взаимно перпендикулярными ребрами тетраэдра, образованного касательной плоскостью и координатными плоскостями. Приняв одно из этих ребер за высоту тетраэдра, найдем, что его объем

, так как точка лежит на данной поверхности. Причем объем не зависит от координат точки касания. Из этого следует, что различные касательные плоскости к данной поверхности образуют с плоскостями координат тетраэдр постоянного, равного, объема.

11. Экстремумы функции нескольких переменных

11.1 Локальный экстремум

Локальный экстремум (т.е. максимум или минимум) для ФНП определяется так же, как и для функции одной переменной.

1°. Функция , определенная в некоторой области, имеет локальный максимум в точке , если в некоторой окрестности этой точки верно неравенство:

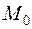
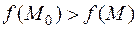
и локальный минимум, если выполняется неравенство:

Очевидно, что в окрестности точки экстремума 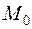приращение функции

сохраняет знак, а именно:

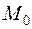
, если — точка максимума

и , если — точка минимума.

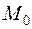
Для исследования функции на экстремум применяют следующие теоремы.

Теорема 1. (Необходимые условия экстремума). Функция нескольких переменных может иметь экстремум только в точках, лежащих внутри области определения функции, в которых все частные производные первого порядка одновременно равны нулю или не существуют.

Такие точки будем называть критическими точками.Точки, в которых все частные производные первого порядка одновременно равны нулю, — стационарными.

Не всякая критическая точка является точкой экстремума. Другими словами, необходимый признак существования экстремума не является достаточным.

Например, для функции ее частные производные и одновременно обращаются в нуль в точке О(0, 0), но:

, а ,

поэтому в точке О(0, 0) экстремума нет.

Таким образом, для исследования функции на экстремум нужно:

1) найти критические точки (в которых все частные первого порядка одновременно обращаются в нуль или не существуют)

2) исследовать функцию в критических точках, используя достаточные признаки экстремума или определение экстремума (исследование знака приращения функции в критической точке).

Теорема 2. (Достаточные признаки экстремума для функции двух переменных).

Пусть — критическая точка функции , а сама функция дважды дифференцируема в критической точке. Обозначим:

, , и .

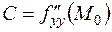
1) если определитель , то — точка экстремума, причем если

— то точка минимума

— точка максимума:

2) если определитель , то функция экстремума в данной точке не имеет;

3) если определитель , то для решения вопроса о наличии или отсутствии экстремума в точке требуются дальнейшие исследования, например, по знаку приращения функции вблизи этой точки.

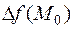
Видео:Уравнения касательной плоскости и нормали к эллиптическому параболоиду (устар.)Скачать

Уравнение касательной плоскости к эллиптическому параболоиду

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Глава 46. Поверхности второго порядка

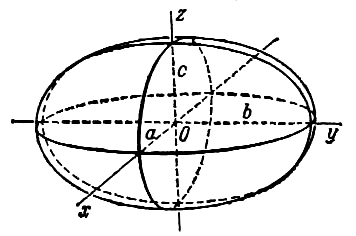
Эллипсоидом называется поверхность, которая в некоторой системе декартовых прямоугольных координат определяется уравнением

(1).

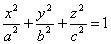
Уравнение (1) называется каноническим уравнением эллипсоида. Величины a, b, c суть полуоси эллипсоида (рис. 1). Если все они различны, эллипсоид называется трехосным; в случае, когда какие-нибудь две из них одинаковы, эллипсоид называется вытянутым, при a=b>c — сжатым. В случае, когда a=b=c , эллипсоид представляет собой сферу.

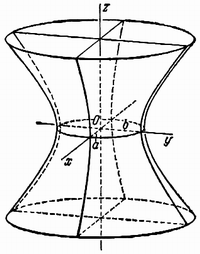
Гиперболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (2)

. (3)

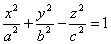
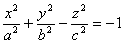
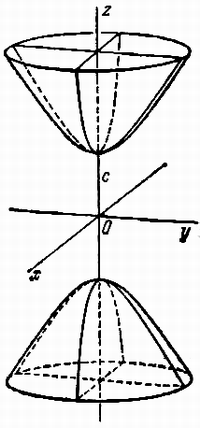
Гиперболоид, определяемый уравнением (2), называется однополостным (рис. 2); гиперболоид, определяемый уравнением (3), — двуполостным (рис. 3); уравнения (2) и (3) называются каноническими уравнениями соответствующих гиперболоидов. Величины a, b, c называются полуосями гиперболоида. В случае однополостного гиперболоида, заданного уравнением (2), только первые из них (а и b ) показаны на рис. 2. В случае двуполостного гиперболоида, заданного уравнением (3), одна из них (именно, с) показана на рис. 3. Гиперболоиды, определяемые уравнениями (2) и (3), при a=b являются поверхностями вращения.

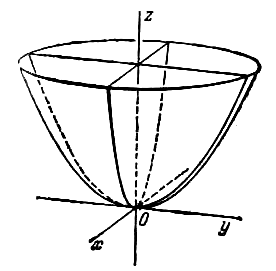
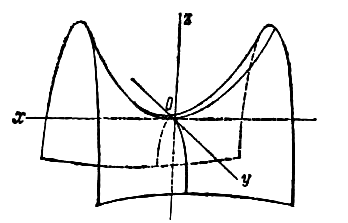
Параболоидами называются поверхности, которые в некоторой системе декартовых прямоугольных координат определяются уравнениями

, (4)

, (5)

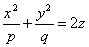
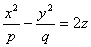
где p и q — положительные числа, называемые параметрами параболоида. Параболоид, определяемый уравнением (4), называется эллиптическим (рис. 4); параболоид, определяемый уравнением (5), — гиперболическим (рис. 5). Уравнения (4) и (5) называют каноническими уравнениями соответствующих параболоидов. В случае, когда p=q , параболоид, определяемый уравнением (4), является поверхностью вращения (вокруг Oz).

Рассмотрим теперь преобразование пространства, которое называется равномерным сжатием (или равномерным растяжением).

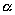
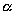
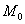
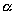
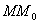
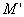
Выберем какую-нибудь плоскость; обозначим ее буквой . Зададим, кроме того, некоторое положительное число q . Пусть М — произвольная точка пространства, не лежащая на плоскости , — основание перпендикуляра, опущенного на плоскость из точки М. Переместим точку М по прямой в новое положение так, чтобы имело место равенство

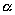
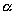
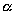
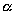
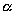
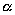
и чтобы после перемещения точка осталась с той же стороны от плоскости , где она была первоначально (рис. 6). Точно так же мы поступим со всеми точками пространства, не лежащими на плоскости ; точки, которые расположены на плоскости , оставим на своих местах. Таким образом, все точки пространства, за исключением тех, что лежат на плоскости , переместятся; при этом расстояние от каждой точки до плоскости изменится в некоторое определенное число раз, общее для всех точек. Описываемое сейчас перемещение точек пространства называется его равномерным сжатием к плоскости ; число q носит название коэффициента сжатия.

Пусть дана некоторая поверхность F ; при равномерном сжатии пространства точки, которые ее составляют, переместятся и в новых положениях сотавят поверхность F ’. Будем говорить, что поверхность F ’ получено из F в результате равномерного сжатия пространства. Оказывается, что многие поверхности второго порядка (все, кроме гиперболического параболоида) можно получить в результате равномерного сжатия из поверхностей вращения).

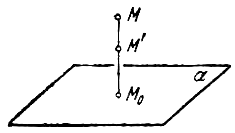
ПРИМЕР. Доказать, что произвольный трехосный эллипсоид

может быть получен из сферы

в результате двух последовательных равномерных сжатий пространства к координатным плоскостям: к плоскости Oxy с коэффициентом сжатия и к плоскости Oxz с коэффициентом сжатия .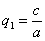

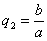
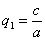
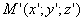
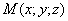
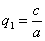
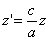
ДОКАЗАТЕЛЬСТВО. Пусть производится равномерное сжатие пространства к плоскости Oxy с коэффициентом и пусть — точка, в которую переходит при этом точка . Выразим координаты x’, y’, z ’ точки М’ через координаты x, y, z точки М. Так как прямая MM ’ перпендикулярна к плоскости Oxy , то x’=x, y’=y . С другой стороны, так как расстояние от точки М’ до плоскости Oxy равно расстоянию от точки М до этой плоскости, умноженному на число , то .

Таким образом, мы получаем искомые выражения:

, , (6)

, , (7)

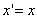
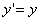
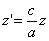
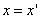
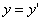
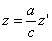
Предположим, что M(x; y; z ) — произвольная точка сферы

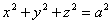
Заменим здесь x, y, z их выражениями (7); получим

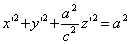
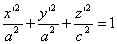
Следовательно, точка M’(x’; y’; z ’) лежит на эллипсоиде вращения. Аналогично, мы должны осуществить сжатие пространства к плоскости Oxz по формулам

, , ;

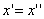
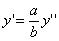
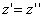
тогда получим трехосный эллипсоид и именно тот, уравнение которого дано в условии задачи.

Отметим еще, что однополостный гиперболоид и гиперболический параболоид суть линейчатые поверхности, то есть они состоят из прямых; эти прямые называются прямолинейными образующими указанных поверхностей.

имеет две системы прямолинейных образующих, которые определяются уравнениями:

, ;

, ,

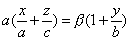
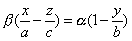
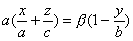
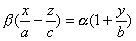
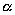
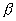
где и — некоторые числа, не равные одновременно нулю. Гиперболический параболоид

также имеет две системы прямолинейных образующих, которые определяются уравнениями

, ;

, .

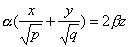
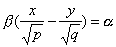
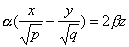
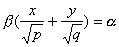
Конической поверхностью, или конусом, называется поверхность, которая описывается движущейся прямой (образующей) при условии, что эта прямая проходит через постоянную точку S и пересекает некоторую определенную линию L . Точка S называется вершиной конуса; линия L — направляющей.

Цилиндрической поверхностью, или цилиндром, называется поверхность, которая описывается движущейся прямой (образующей) при услвоии, что эта прямая имеет постоянное направление и пересекает некоторую определенную линию L (направляющую).