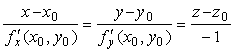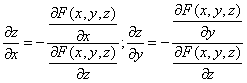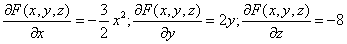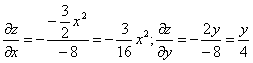Касательной плоскостью к поверхности σ в её точке М0 называется плоскость, в которой лежат касательные ко всем кривым, проведённым на поверхности σ через точку М0.
Уравнение касательной плоскости к поверхности, заданной уравнением z = f(x,y) , в точке M0(x0,y0,z0) имеет вид:
Пример №1 . Поверхность задана уравнением x 3 +5y . Найти уравнение касательной плоскости к поверхности в точке M0(0;1).
Решение. Запишем уравнения касательной в общем виде: z — z0 = f’x(x0,y0,z0)(x — x0) + f’y(x0,y0,z0)(y — y0)
По условию задачи x0 = 0 , y0 = 1 , тогда z0 = 5
Найдем частные производные функции z = x^3+5*y :
f’x(x,y) = (x 3 +5•y)’x = 3•x 2
f’x(x,y) = (x 3 +5•y)’y = 5
В точке М0(0,1) значения частных производных:
f’x(0;1) = 0
f’y(0;1) = 5
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z — 5 = 0(x — 0) + 5(y — 1) или -5•y+z = 0
Пример №2 . Поверхность задана неявным образом y 2 -1/2*x 3 -8z. Найти уравнение касательной плоскости к поверхности в точке M0(1;0;1).
Решение. Находим частные производные функции. Поскольку функция задана в неявном виде, то производные ищем по формуле:
Для нашей функции:
Тогда:
В точке М0(1,0,1) значения частных производных:
f’x(1;0;1) = -3 /16
f’y(1;0;1) = 0
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0: z — 1 = -3 /16(x — 1) + 0(y — 0) или 3 /16•x+z- 19 /16 = 0
Пример . Поверхность σ задана уравнением z= y/x + xy – 5x 3 . Найти уравнение касательной плоскости и нормали к поверхности σ в точке М0(x0, y0, z0), принадлежащей ей, если x0 = –1, y0 = 2.
Найдем частные производные функции z= f(x, y) = y/x + xy – 5x 3 :
fx’(x, y) = (y/x + xy – 5x 3 )’x = – y/x 2 + y – 15x 2 ;
fy’ (x, y) = (y/x + xy – 5x 3 )’y = 1/x + x.
Точка М0(x0, y0, z0) принадлежит поверхности σ, поэтому можно вычислить z0, подставив заданные x0 = –1 и y0 = 2 в уравнение поверхности:
Пример №1 . Дана функция z=f(x,y) и две точки А(х0, y0) и В(х1,y1). Требуется: 1) вычислить значение z1 функции в точке В; 2) вычислить приближенное значение z1 функции в точке В исходя из значения z0 функции в точке А, заменив приращение функции при переходе от точки А к точке В дифференциалом; 3) составить уравнение касательной плоскости к поверхности z = f(x,y) в точке C(x0,y0,z0).
Решение.
Запишем уравнения касательной в общем виде:
z — z0 = f’x(x0,y0,z0)(x — x0) + f’y(x0,y0,z0)(y — y0)
По условию задачи x0 = 1, y0 = 2, тогда z0 = 25
Найдем частные производные функции z = f(x,y)x^2+3*x*y*+y^2:
f’x(x,y) = (x 2 +3•x•y•+y 2 )’x = 2•x+3•y 3
f’x(x,y) = (x 2 +3•x•y•+y 2 )’y = 9•x•y 2
В точке М0(1,2) значения частных производных:
f’x(1;2) = 26
f’y(1;2) = 36
Пользуясь формулой, получаем уравнение касательной плоскости к поверхности в точке М0:
z — 25 = 26(x — 1) + 36(y — 2)
или
-26•x-36•y+z+73 = 0
Пример №2 . Написать уравнения касательной плоскости и нормали к эллиптическому параболоиду z = 2x 2 + y 2 в точке (1;-1;3).
Скачать решение
- VMath
- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- Содержание
- Поверхности. Касательная плоскость и нормаль
- Краткие теоретические сведения
- Способы задания поверхностей
- Решение задач
- Задача 1 (Феденко №544)
- Задача 2 (Феденко № 546)
- Задача 3 (Феденко №528)
- Решение задачи 3
- Касательная плоскость. Нормаль
- Краткие теоретические сведения
- Решение задач
- Задача 1 (Феденко №574)
- Задача 2
- Задача 3
- Задача 4
- Задача 5 (Феденко №594)
- Решение задачи 5
- Эллипс
- Определение эллипса.
- Фокусы, эксценриситет и директрисы эллипса.
- Уравнение касательной к эллипсу.
- 🎦 Видео
Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Видео:Математика без Ху!ни. Уравнение касательной.Скачать
Поверхности. Касательная плоскость и нормаль
Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать
Краткие теоретические сведения
Способы задания поверхностей
Рассматриваем вектор–функцию двух скалярных аргументов: $$vec=vec(u,v).$$ Годографом такой функции является поверхность.
Запишем четыре способа задания поверхности: 1. Векторное уравнение: $$vec=vec(u,v).$$ 2. Параметрическое уравнение: $$x=x(u,v),,, y=y(u,v),,, z=z(u,v).$$ 3. Неявное уравнение: $$varPhi(x,y,z)=0.$$ 4. Явное уравнение: $$z=z(x,y).$$
Поверхность называется регулярной ($k$ раз дифференцируемой), если у каждой точки этой поверхности есть окрестность, допускающая регулярную параметризацию (то есть функции $x(u,v), y(u,v),z=z(u,v)$ $k$ раз непрерывно дифференцируемы). При $k=1$ поверхность называется гладкой.
Регулярная поверхность в окрестности каждой своей точки допускает бесчисленное множество параметризаций.
Кривая, лежащая на поверхности $vec=vec(u,v)$, задается уравнениями $$ u=u(t),,, v=v(t).$$ Линии $u=mbox$, $v=mbox$ являются координатными линиями данной параметризации поверхности.
Видео:Как написать уравнения касательной и нормали | МатематикаСкачать
Решение задач
Задача 1 (Феденко №544)
Дана поверхность begin x=u+v, ,, y=u-v,,, z=uv. end Проверить, принадлежат ли ей точки $A(4,2,3)$ и $B(1,4,-2)$.
Ответ. Точка $A$ принадлежит, так как ее координаты удовлетворяют системе уравнений, задающих поверхность. Точка $B$ не принадлежит поверхности.
Задача 2 (Феденко № 546)
Найдите неявное уравнение поверхности, заданной параметрическими уравнениями: begin begin x & = x_0 + a,mbox,u,mbox,v, \ y & = y_0 + b,mbox,u,mbox,v, \ z & = z_0 + c,mbox,u. end end
Ответ. Эллипсоид с полуосями $a$, $b$, $c$ и центром в точке $(x_0, y_0, z_0)$: begin frac+frac+frac=1. end
Задача 3 (Феденко №528)
В плоскости $xOz$ задана кривая $x=f(u)$, $z=g(u)$, не пересекающая ось $Oz$. Найдите параметризацию поверхности, полученной при вращении этой кривой вокруг оси $Oz$.
Решение задачи 3
Произвольная точка $M$, принадлежащая кривой и имеющая координаты $x_0=f(u_0)$, $y_0=0$, $z_0=g(u_0)$, движется по окружности с центром на оси $Oz$ и радиусом $R=f(u_0)$ в плоскости, параллельной плоскости $xOy$: $z=g(u_0)$. Поэтому изменение ее координат можно записать следующими уравнениями: begin left< begin x_0 & = & f(u_0),mbox,v, \ y_0 & = & f(u_0),mbox,v, \ z_0 & = & g(u_0). \ end right. end
Поскольку точка $M$ произвольная, уравнение искомой поверхности: begin left< begin x & = & f(u),mbox,v, \ y & = & f(u),mbox,v, \ z & = & g(u). \ end right. end
Видео:Уравнения касательной плоскости и нормали к поверхностиСкачать
Касательная плоскость. Нормаль
Видео:3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать
Краткие теоретические сведения
Пусть $vec=vec(u,v)in C^1$ — поверхность, проходящая через точку $P(u_0, v_0)$. Пусть $u=u(t)$, $v=v(t)$ — уравнения гладкой кривой, проходящей через точку $P(u_0, v_0)$ и лежащей на заданной поверхности.
Пусть точка $P$ не является особой, то есть ранг матрицы begin left( begin x_u & y_u & z_u \ x_v & y_v & z_v \ end right) end в точке $P$ равен $2$ (для особой точки ранг меньше $2$). Если поверхность задана неявно $varPhi(x,y,z)=0$, то в не особой точке $P$ выполняется условие: $varPhi_x^2+varPhi_y^2+varPhi_z^2neq0.$
Касательная к кривой $u=u(t)$, $v=v(t)$ на поверхности $vec=vec(u,v)$ определяется вектором: begin displaystylefrac<dvec>
Обозначения:
— $vec=$ — радиус-вектор произвольной точки касательной плоскости.
— $vec=$ — радиус вектор точки $P(u_0, v_0)$.
— Частные производные $x_u$, $y_u$, $z_u$, $x_v$, $y_v$, $z_v$ вычисляются в точке $P(u_0, v_0)$.
Уравнение касательной плоскости:
1. Если поверхность задана векторно, то уравнение касательной плоскости можно записать через смешанное произведение трех линейно зависимых векторов: $$ left(vec-vec, , vec_u, , vec_v right)=0. $$ 2. Если поверхность задана параметрически, запишем определитель: begin left| begin X-x & Y-y & Z-z \ x_u & y_u & z_u\ x_v & y_v & z_v\ end right|=0 end 3. Если поверхность задана неявным уравнением: begin varPhi_x(X-x)+varPhi_y(Y-y)+varPhi_z(Z-z)=0. end 4. В случая явного задания поверхности, уравнение касательной плоскости примет вид: begin (Z-z)=z_x(X-x)+z_y(Y-y). end
Нормалью поверхности в точке $P$ называется прямая, проходящая через $P$ перпендикулярно касательной плоскости в этой точке.
Уравнение нормали:
1.$$ vec=vec + lambdavec, ,, vec=vec_utimesvec_v. $$ 2. begin displaystylefrac< left| begin y_u & z_u\ y_v & z_v\ end right|>= displaystylefrac< left| begin z_u & x_u\ z_v & x_v\ end right|>= displaystylefrac< left| begin x_u & y_u\ x_v & y_v\ end right|>. end 3. begin displaystylefrac=displaystylefrac=displaystylefrac. end 4. begin displaystylefrac=displaystylefrac=displaystylefrac. end
Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать
Решение задач
Задача 1 (Феденко №574)
Дана поверхность begin x=u,mbox,v,,, y=u,mbox,v,,, z=u. end Написать:
а) уравнение касательной плоскости к поверхности;
б] уравнение нормали к поверхности;
в) касательной к линии $u=2$
в точке $Mleft(u=2, v=displaystylefracright)$ поверхности.
Задача 2
Через точки $A(0,1,0)$ и $B(1,0,0)$ провести плоскость, касательную к поверхности $vec=$.
Ответ. $z=0, -2X-2Y+Z+2=0$.
Задача 3
Построить касательную плоскость к поверхности $y=x^2+z^2$, перпендикулярную вектору $vec$.
Задача 4
Через точку $M(1,2,1)$ провести плоскость, касательную к поверхности $x^2+y^2-z^2=0$.
Ответ. $X-Z=0$, $3X-4Y+5Z=0$.
Задача 5 (Феденко №594)
Докажите, что поверхности begin z=mbox(xy), ,, x^2-y^2=a end ортогональны в точках их пересечения.
Решение задачи 5
Запишем направляющие векторы нормалей к поверхностям, проведенным в точках их пересечения: begin begin vec_1&=left<frac<mbox^2(x_0y_0)>,frac<mbox^2(x_0y_0)>,-1right>,\ vec_2&=left. end end Скалярные произведения векторов $n_1$ и $n_2$ равны нулю, следовательно векторы ортогональны. begin n_1cdot n_2=0. end
Видео:Уравнение касательной плоскости к эллипсоиду и двуполостному гиперболоидуСкачать
Эллипс
Видео:§3.6. Касательная плоскость и нормаль к поверхностиСкачать
Определение эллипса.
Напомним, что мы назвали эллипсом линию, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
frac<x^><a^>+frac<y^><b^>=1label
$$
при условии (a geq b > 0).
Из уравнения eqref следует, что для всех точек эллипса (|x| leq a) и (|y| leq b). Значит, эллипс лежит в прямоугольнике со сторонами (2a) и (2b).
Точки пересечения эллипса с осями канонической системы координат, имеющие координаты ((a, 0)), ((-a, 0)), ((0, b)) и ((0, -b)), называются вершинами эллипса. Числа (a) и (b) называются соответственно большой и малой полуосями эллипса.
Рис. 8.1. Эллипс
В каноническое уравнение входят только квадраты координат. Поэтому, если координаты ((x, y)) какой-либо точки /(M) ему удовлетворяют, то ему удовлетворяют и координаты ((-x, y)), ((x, -y)) и ((-x, -y)) точек (M_), (M_) и (M_) (рис. 8.1). Следовательно, справедливо следующее утверждение.
Оси канонической системы координат являются осями симметрии эллипса, а начало канонической системы — его центром симметрии.
Внешний вид эллипса проще всего описать сравнением с окружностью радиуса (a) с центром в центре эллипса: (x^+y^=a^). При каждом (x) таком, что (|x| 
Рис. 8.2. Сжатие окружности к эллипсу. Ординаты всех точек уменьшаются в отношении (b/a).
Видео:Частные производные второго порядка. Уравнение касательной плоскости и нормали к поверхностиСкачать
Фокусы, эксценриситет и директрисы эллипса.
У эллипса есть две замечательные точки, которые называются его фокусами.
Фокусами называются точки (F_) и (F_) с координатами ((c, 0)) и ((-c, 0)) в канонической системе координат (рис. 8.3).
Рис. 8.3. Фокусы эллипса.
Для окружности (c=0), и оба фокуса совпадают с центром. Ниже мы будем предполагать, что эллипс не является окружностью.
Отметим, что (varepsilon Утверждение 2.
Расстояние от произвольной точки (M(x, y)), лежащей на эллипсе, до каждого из фокусов (рис. 8.3) является линейной функцией от ее абсциссы (x):
$$
r_=|F_M|=a-varepsilon x, r_=|F_M|=a+varepsilon x.label
$$
Очевидно, что (r_^=(x-c)^+y^). Подставим сюда выражение для (y^), найденное из уравнения эллипса. Мы получим
$$
r_^=x^-2cx+c^+b^-frac<b^x^><a^>.nonumber
$$
Учитывая равенство eqref, это можно преобразовать к виду
$$
r_^=a^-2cx+frac<c^x^><a^>=(a-varepsilon x)^.nonumber
$$
Так как (x leq a) и (varepsilon Утверждение 3.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы сумма ее расстояний до фокусов равнялась большой оси эллипса (2a).
Необходимость. Если мы сложим равенства eqref почленно, то увидим, что
$$
r_+r_=2a.label
$$
Достаточность. Пусть для точки (M(x, y)) выполнено условие eqref, то есть
$$
sqrt<(x-c)^+y^>=2a-sqrt<(x+c)^+y^>.nonumber
$$
Возведем обе части равенства в квадрат и приведем подобные члены:
$$
xc+a^=asqrt<(x+c)^+y^>.label
$$
Это равенство также возведем в квадрат и приведем подобные члены, используя соотношение eqref. Мы придем к (b^x^+a^y^=a^b^), равносильному уравнению эллипса eqref.
Рис. 8.4. Фокусы и директрисы эллипса.
Для того чтобы точка лежала на эллипсе, необходимо и достаточно, чтобы отношение ее расстояния до фокуса к расстоянию до соответствующей директрисы равнялось эксцентриситету эллипса (varepsilon).
Видео:7. ФНП. Касательная плоскость и нормальная прямая к поверхностиСкачать
Уравнение касательной к эллипсу.
Выведем уравнение касательной к эллипсу, заданному каноническим уравнением. Пусть (M_(x_, y_)) — точка на эллипсе и (y_ neq 0). Через (M_) проходит график некоторой функции (y=f(x)), который целиком лежит на эллипсе. (Для (y_ > 0) это график (f_(x)=bsqrt<1-x^/a^>), для (y_ Утверждение 5.
Касательная к эллипсу в точке (M_(x_, y_)) есть биссектриса угла, смежного с углом между отрезками, соединяющими эту точку с фокусами.
Рис. 8.5.
🎦 Видео
Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать
Касательная плоскость и нормаль к поверхностиСкачать
Касательная плоскость и нормаль к поверхности в заданной точкеСкачать
Начертательная геометрия. Касательная плоскость и нормаль к поверхности конуса.Скачать
10 класс, 43 урок, Уравнение касательной к графику функцииСкачать
Касательная плоскость и нормаль в точкеСкачать
Касательная плоскость и нормаль к поверхностиСкачать
Математика без Ху!ни. Уравнение плоскости.Скачать
УРАВНЕНИЕ КАСАТЕЛЬНОЙ И НОРМАЛИ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХСкачать
