Уравнение касательной к плоской кривой

Видео:Уравнения касательной и нормали к кривой, заданной в неявном видеСкачать

Касательная и нормаль к кривой

Касательная прямая — прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

Прямая, проходящая через точку касания, перпендикулярно касательной, называется нормалью к кривой.

Если кривая определена уравнением $y=f(x)$, то уравнение касательной к ней в точке $M(x_0;y_0)$ имеет вид:

а уравнение нормали:

Задание. Написать уравнение касательной и нормали к кривой $y=x^2-3x+4$ в точке с абсциссой $x_0=0$.

Решение. Находим значение функции в заданной точке:

Далее вычислим значение производной функции в точке $x_0=0$:

а тогда уравнение касательной запишется в виде:

или после упрощения:

$$y-4=-frac(x-0) Rightarrow x-3 y+12=0$$

Ответ. Уравнение касательной: $3x+y-4=0$

Уравнение нормали: $x-3y+12=0$

Видео:Как написать уравнения касательной и нормали | МатематикаСкачать

Угол между кривыми

Углом между кривыми на плоскости в их общей точке $M(x_0;y_0)$ называется наименьший из двух возможных углов между касательными к этим кривым в данной точке. Если уравнения касательных, проведенных к кривым $y=f_1(x)$ и $y=f_2(x)$, соответственно $y=k_x+b_$ и $y=k_x+b_2$, то тангенс угла между кривыми определяется соотношением:

Задание. Найти тангенс угла между кривыми $y=x^2-1$ и $y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.

Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:

Таким образом, искомая точка $x=1$.

Далее находим производные заданных функций в найденной точке:

Итак, искомый тангенс:

Ответ. $operatorname phi=frac$

Видео:Математика без Ху!ни. Уравнение касательной.Скачать

Лекция Плоские кривые. Способы задания плоской кривой.Длина плоской кривой. Касательная и нормаль к кривой. Кривизна кривой. Эволюта и эвольвента

III . ПЛОСКИЕ КРИВЫЕ.

1. Способы задания плоских кривых.

2. Уравнения касательной и нормали.

3. Формулы для нахождения единичного вектора нормали и кривизны.

4. Уравнение эволюты.

3.1 СПОСОБЫ ЗАДАНИЯ ПЛОСКОЙ КРИВОЙ.

Кривая, у которой кручение в каждой точке равно нулю, располагается в плоскости и поэтому называется плоской. В качестве такой плоскости выбирают плоскость хОу.

Геометрию плоских кривых можно получить как частный случай геометрии кривых в пространстве, но при таком подходе могут ускользнуть многие своеобразные их особенности. В связи с этим теория плоских кривых строится независимо от теории кривых в пространстве.

Кривую на плоскости можно задать уравнениями различных видов, наиболее распространенными из которых являются:

а) векторное уравнение , (3.1)

б) векторно-параметрическое уравнение (3.2)

в) координатно-параметрические уравнения

г) уравнение в несимметричной форме

или (3.5)

Заметим, что присоединив к уравнению (3.4) тождество х=х , получим параметрические уравнения х=х, y = f ( x ). Они отличаются от уравнений (3.3) тем, что за параметр принята абсцисса точка кривой.

В частности, если какая-либо точка кривой не является особой (т.е. отлична от нуля по крайней мере одна из производных в этой точке), то в ее окрестности уравнение (3.6) можно разрешить или относительно у (при ), и тогда получим уравнение (3.4), или относительно х (при ), тогда получим уравнение (3.5).

3.2 ДЛИНА ПЛОСКОЙ КРИВОЙ.

Длиной кривой называется верхняя грань всех возможных ломаных, вписанных в данную кривую. В частности, если кривая задана векторно-параметрическим уравнением и функция непрерывна вместе со своей производной на , то она спрямляема.

а) Длина кривой в прямоугольных координатах .

Если плоская кривая задана уравнением , где функция непрерывна вместе со своей производной на [ a , b ], то она спрямляема и ее длина выражается формулой

(3.7)

Если кривая задана параметрическими уравнениями и функции непрерывно дифференцируемы на [ T ₁ , T ₂ ], то ее длина выражается формулой:

(3.8)

б) Длина кривой в полярных координатах.

Если кривая задана в полярных координатах уравнением и функция непрерывна вместе со своей производной на , то ее длина выражается формулой

(3.9)

Пример 3.1 Найти длину полукубической параболы ay 2 = x 3 , a >0 от х =0 до х=5а .

Решение: Из уравнений кривой следует, что полукубическая парабола симметрична относительно оси абсцисс (замена у= ‑у не изменяет уравнения) и расположена в правой полуплоскости координатной полуплоскости хОу ( х не может быть отрицательным). Вычислим длину одной ветви кривой ОА.

Из уравнения кривой находим .

По формуле (3.7) получим:

.

Длина кривой равна S =670 а /27.

Пример 3.2 Вычислить длину кардиоиды .

Решение: Однозначная ветвь функции r соответствует изменению параметра в промежутке , при этом кривая симметрична относительно полярной оси. При изменении от 0 до полярный радиус r опишет половину кривой. Половину длины кардиоиды найдем, используя формулу (3.9):

Длина всей кардиоиды S =8 a .

3.3 КАСАТЕЛЬНАЯ И НОРМАЛЬ К КРИВОЙ.

Единичный вектор направленной касательной, как мы показали выше (1.7), находится как орт производной радиус-вектора: .

На практике иногда удобнее в качестве направляющего вектора касательной брать вектор (или любой ему коллинеарный вектор) и уравнение касательной в точке записать в виде:

(3.10)

или . (3.11)

В качестве направляющего вектора нормали можно взять единичный вектор главной нормали , или, что на практике гораздо проще, вектор , ортогональный вектору , тогда уравнение нормали будет иметь вид:

(3.12)

или . (3.13)

Если кривая задана уравнением в несимметричной форме (3.4), то касательная и нормаль соответственно имеют уравнения

(3.14)

(3.15)

г) Если кривая задана уравнением в симметричной форме (3.6), то касательная и нормаль соответственно имеют уравнения

(3.16)

(3.17)

Пример 3.3 Составить уравнение касательной и нормали к кривой y = x 3 -2 в точке А(2,3).

Решение: Используем уравнение касательной (3.14) и нормали для кривой, заданной в несимметричной форме. Запишем уравнение пучка прямых, проходящих через данную точку А(2,3): y -3= k ( x -2),

где k – угловой коэффициент прямой (в данном случае произвольный параметр). Для определения k , соответствующего касательной и нормали к кривой, найдем производную при х =2:

Следовательно, для касательной k =12, для нормали k = ‑ 1/12. Подставляя эти значения в уравнение пучка прямых, получим уравнение касательной

.

Пример 3.4 Составить уравнение касательной и нормали к декартовому листу х 3 +у 3 -3аху=0, а>0 (рис.9) в точке А ( 3а/2;3а/2 ).

Решение. Используем уравнения касательной (3.16) и нормали (3.17) для кривой заданной в симметричной форме. Записав исходное уравнение в виде F( x,y )=0 , найдем:

Подставляя значения производных в уравнение касательной

и нормали: ,

получим уравнение касательной у=3а-х , и уравнение нормали у=х .

3.4 КРИВИЗНА КРИВОЙ. ЭВОЛЮТА И ЭВОЛЬВЕНТА КРИВОЙ.

Если кривая задана уравнением у=у(х), то ее кривизна определяется по формуле:

(3.18)

В случае векторно-параметрического задания кривой

(3.19)

Радиус кривизны в данной точке:

(3.20)

Всякая прямая, проходящая через точку кривой и перпендикулярная касательной в этой точке, называется нормалью к кривой в данной точке. Вектор нормали к кривой, направленный в сторону центра кривизны и указывающий направление, в котором кривая в окрестности рассматриваемой точки отклоняется от своей касательной, называется вектором главной нормали. Множество центров кривизны кривой образуют ее эволюту. В случае векторно-параметрического задания кривой уравнение эволюты имеет вид (2.17): , и координаты центра кривизны определяются формулами:

, (3.21)

Если кривая задана уравнением y = f ( x ) , то

, (3.22)

Исходная кривая по отношению к своей эволюте называется эвольвентой.

Пример 3.5 Найти кривизну и радиус кривизны параболы у=х 2 в произвольной точке х.

Решение: Кривизну параболы найдем, подставляя в (3.18):

Эта величина принимает наибольшее значение при х =0, для которого k =2. Радиус кривизны связан с кривизной соотношением (3.20), поэтому

Наименьший радиус кривизны в точке (0,0).

Пример 3.6 Найти радиус кривизны и эволюту эллипса .

Решение: Представим уравнение эллипса в параметрическом виде:

Подставляя в формулы (3.19) и (3.20), получим

.

Уравнение эволюты найдем по формуле (3.21):

Таким образом, эволютой эллипса является астроида.

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

Геометрическое применение производной

Вы будете перенаправлены на Автор24

Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать

Что такое касательная и нормаль к кривой

Касательная — прямая которая совпадает и проходит через точку кривой с точностью до первого порядка.

Нормаль к кривой — прямая перпендикулярно проходящая через точку касания.

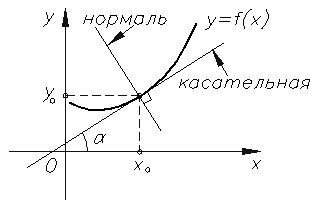
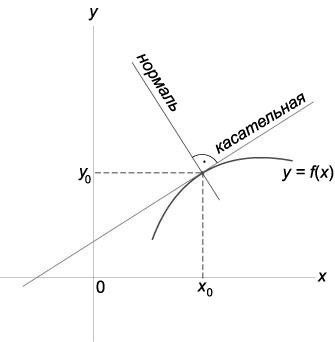
Рисунок 1. Нормаль и касательная к кривой

Для кривой вида y = f(x) уравнение касательной в точке М(x0,y0):

Для кривой вида y = f(x) уравнение касательной в точке М(x0,y0):

Написать уравнение касательной и нормали к кривой в точке с абсциссой $x_0=1$:

1. Найдем значение функции в точке: [y_ =3cdot 1^ -2cdot 1+11=12]
2. Найдем производную в данной точке: [y'(x_ )=left(3x^ -2x+11right) <> =6x-2] [y'(1)=6cdot 1-2=4]
3. Запишем уравнение касательной: [y-y_ =y`(x_ )(x-x_ )] [y-12=4(x-1)] [y-4x-8=0]
4. Запишем уравнение нормали: [y-12=-frac(x-1)] [4y+x-49=0]

Угол между двумя кривыми в точке М(x0,y0) является наименьшим из возможных углов между касательными. Пусть уравнения касательных имеют вид:

Тогда тангенс угла между двумя кривыми находится по формуле:

Найти тангенс угла между кривыми, в точке имеющей большую абсциссу.

Для того чтобы определить точки пересечения кривых необходимо решить систему уравнений: [left<begin<y=2x^-3> \ endright. ] [2x^ -3=4x-2] [2x^ -4x=1] [2x(x-2)=1]

Значит, кривые пересекаются в точках 0,5 и 2. Максимальной, из которых, является точка x = 2.

Готовые работы на аналогичную тему

Видео:Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.Скачать

Что такое длина касательной и нормали, подкасательная и поднормаль

Длина отрезка от пересечения касательной оси ОХ до пересечения с нормалью или кривой называется длиной касательной.

Проекция отрезка от пересечения касательной оси ОХ до пересечения с нормалью или кривой на ось Ох называется подкасательной (ST).

Длина отрезка от пересечения нормали с касательной или кривой до точки соприкосновения с осью Ох называется длиной нормали, а проекция отрезка на ось — поднормалью (SN).

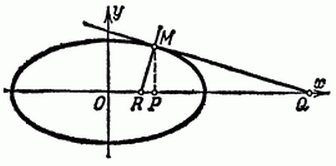
Найти длину подкасательной и поднормали для эллипса x = acost, y = bsint

Рисунок 2. Эллипс

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 15 12 2021

🎬 Видео

3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать

Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать

Касательная прямая и нормальная плоскость кривой | ФНП 2.3Скачать

Дифференцирование. Запись уравнения касательной к кривой. Урок 6Скачать

Уравнения касательной и нормали к кривойСкачать

14.1. Касательная к параметрически заданной функцииСкачать

Касательная и нормаль к кривойСкачать

Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Геометрический смысл производной. Уравнение касательнойСкачать

найти уравнение касательной к параметрической кривойСкачать

Касательная к графику функции в точке. 10 класс.Скачать

Уравнения касательной плоскости и нормали к поверхностиСкачать

Уравнение касательной в точке. Практическая часть. 2ч. 10 класс.Скачать

Как составить уравнение касательной и нормали к графику функцииСкачать