Уравнение изотермы адсорбции в микропорах (2 видео)

Основы теории адсорбции на пористых адсорбентах

В 1914 г. Поляни предложил рассматривать процесс адсорбции аналогично сжатию молекул адсорбтива в некотором поле адсорбционных сил вблизи поверхности адсорбента. Этот процесс протекает таким образом, что на поверхности адсорбента в результате сжатия адсорбтива в поле адсорбционных сил формируется жидкая пленка, т.е. происходит конденсация адсорбтива. Для упрощения Поляни допускал, что в поле адсорбционных сил газ подчиняется закону Клайперона-Менделеева. Это означает, что адсорбент химически инертный и адсорбция протекает только в результате физического взаимодействия между молекулами адсорбента и адсорбтива.

В этом случае можно было ввести количественную характеристику поля адсорбционных сил, а именно, адсорбционный потенциал e, равный работе сжатия одного моля газа или пара от равновесного давления Р в объеме до давления насыщения P_s. Этот потенциал можно также рассматривать как работу перемещения одного моля газа с бесконечно большого расстояния на поверхность адсорбента.

Из химической термодинамики известно, что работа сжатия идеального газа вплоть до его конденсации может быть описана уравнением

. (1.3.55)

Уравнение (1.3.55) является основным уравнением в теориях адсорбции на микропористых адсорбентах. Очевидно, что потенциал адсорбционных сил в трактовке Поляни является не чем иным, как дифференциальной свободной энергией адсорбции, т.е. e = — DG_а.

Дубинин и Радушкевич положили потенциальную теорию Поляни в основу теории адсорбции газов на микропористых адсорбентах. Вместо понятия «адсорбционный потенциал» они предпочитали использовать термин дифференциальная молярная работа адсорбции, что несомненно терминологически более правильно. Одна из основных предпосылок теории, развитой Дубининым и Радушкевичем, — не послойная адсорбция на стенках пор адсорбента, а объемное заполнение пор. Поэтому вторым параметром для описания адсорбции на микропористых адсорбентах является степень заполнения микропор, определяемая выражением

, (1.3.56)

где W₀— общий объем микропор, W– объем пор, заполненных при некотором относительном давлении P/P_s.

Учитывая, что в микропорах поля адсорбционных сил перекрываются, Дубинин и Радушкевич приняли предположение, что распределение степени заполнения микропор по дифференциальной молярной работе адсорбции описывается гауссовой кривой. Такое предположение приводит к выражению

, (1.3.57)

где k — некоторая постоянная, зависящая от природы адсорбата и адсорбента.

Учитывая уравнение (1.3.55), можно записать

. (1.3.58)

, (1.3.59)

где D = k(2,3RT) 2 – постоянная уравнения Дубинина-Радушкевича.

Обычно для определения общей пористости адсорбентов это уравнение выражают в линейной — логарифмической форме:

. (1.3.60)

Адсорбцию рассчитывают как , где V_m — молярный объем адсорбата.

Для того, чтобы определить, к какому типу адсорбентов – гладкому или микропористому – относится исследуемый адсорбент, требуется провести предварительную обработку экспериментальных данных.

Рис.1.30. Влияние микропористости на адсорбцию газа на твердом адсорбенте. Адсорбенты: 1- непористый; 2- микропористый

На рис. 1.30 приведены изотермы адсорбции на непористом (1) и микропористом (2) адсорбентах. Микропористость образуется, например, после графитизации сажи при различных температурах или в результате спрессовывания порошков каких-либо твердых тел. На этом рисунке показан график адсорбции на необработанном (1) и графитизированном (2) образцах сажи. В принципе характер изотерм идентичен – они соответствуют типу II изотерм, но видно, что увеличивается величина адсорбции при том же равновесном давлении, которое в случае микропористых адсорбентов составляет сотые доли от давления насыщения. Для того чтобы выявить образование микропор используют метод построения, так называемых, t-графиков Липпенса-де-Бура, пример которого схематично показан на рис. 1.31. Этот график базируется на стандартной изотерме, для построения которой в качестве независимой переменной используется средняя толщина адсорбционной пленки t = (n/n_m)d, где n и n_mравновесная адсорбция и предел заполнения одного монослоя, выраженные как число молей адсорбированного газа на грамм адсорбента, d — толщина монослоя адсорбированного вещества (поперечное сечение адсорбированных молекул). Если анализируемая изотерма идентична стандартной, то график должен выражаться прямой линией, проходящей через начало координат (на рис. 1.31. это прямая 1). В этом случае можно говорить об адсорбции на гладком адсорбенте, на поверхности которого формируется пленка адсорбата, и изотерма должна описываться уравнением теории полимолекулярной адсорбции БЭТ. Если же после обработки экспериментальных данных в координатах стандартной изотермы будет получен график, не проходящий через начало координат (кривая 2 рис. 3.4), то это свидетельствует о микропористости адсорбента и обработку экспериментальных данных следует вести по уравнению теории Дубинина.

Рис. 1.31. Изотермы адсорбции в форме t-графика. Адсорбенты:

1- непористый; 2- микропористый

Пример зависимости адсорбции на микропористом адсорбенте в координатах линейной формы уравнения Дубинина-Радушкевича приведен на рис. 1.32. По отрезку на оси ординат находят предел адсорбции и определяют общую пористость адсорбента. Следует отметить, что адсорбция на полностью микропористых адсорбентах часто выражается изотермой типа I, которая иногда аппроксимируется уравнением Ленгмюра. Микропористые адсорбенты насыщаются, как правило, при низких относительных давлениях (Р/Р_s)

Содержание

Теория объемного заполнения микропор (ТОЗМ).
Уравнение изотермы адсорбции в микропорах
Мономолекулярная адсорбция. Изотерма адсорбции Ленгмюра
Полимолекулярная адсорбция. Уравнение БЭТ
Энергетические параметры адсорбции на однородной поверхности
Взаимодействие частиц в адсорбционном слое и классификация изотерм адсорбции
🎥 Видео

Видео:Поверхностные явления. Адсорбция.Скачать

Теория объемного заполнения микропор (ТОЗМ).

М.М.Дубинин с сотрудниками разработали теорию равновесной адсорбции вещества на микропористых адсорбентах; термодинамические аспекты этой теории разработаны Б.П. Берингом и В.В. Серпинским. Согласно T03М адсорбция характеризуется объемным заполнением адсорбционного пространства микропор без последовательного образования слоев. Основным геометрическим параметром микропористого адсорбента является объем микропор, а не площадь их поверхности. Рассматриваемая теория является термодинамической, и в основу ее положены такие термодинамические функции, как свободная энергия, энтропия и энтальпия.

Если для вычисления изменения этих функций в качестве стандартного состояния принять объемную жидкую фазу адсорбата, находящуюся в равновесии с ее насыщенным паром при давлении р_s, или летучести f_s, то дифференциальная максимальная молярная работа адсорбции А равна по величине, но противоположна по знаку, изменению свободной энергии Гиббса DG

В уравнении (7.4) и всех последующих выражениях неидеальность газовой фазы легко учесть, вводя летучесть вместо давления. Дифференциальная молярная энтропия адсорбата DS, отсчитываемая от уровня энтропии, соответствующего адсорбируемому веществу в виде жидкости при температуре опыта:

Изменение энтальпии DI равно по абсолютному значению дифференциальной теплоте адсорбции q:

DI = — q = DG+ T D S= — А + T( ¶ A / ¶ T)_a. (7.6)

Используя известный в математической статистике закон распределения Вейбулла, М.М. Дубинин и В.А. Астахов получили уравнение изотермы адсорбции в аналитической форме:

где q — степень заполнения объема микропор; a₀ — предельная величина адсорбции при температуре Т; Е — характеристическая свободная энергия адсорбции; n — безразмерный параметр (при адсорбции на углеродных адсорбентах n = 2, на микропористых n = 3, на цеолитах n = 3. 6).

Зависимость А = E f(q,n) названа характеристической кривой.

Основные исходные положения ТОЗМ: постоянство объема адсорбционного пространства, т.е. объема микропор адсорбента; температурная независимость (инвариантность) характеристической кривой (следствием является постоянство параметров Е и n); подобие характеристических кривых для различных паров.

Первое исходное положение ТОЗМ позволяет определить предельную величину адсорбции а₀ при любой температуре Т, если она определена при стандартной температуре Т₀ по уравнению а₀ = а₀ 0 ехр[–a(Т- Т₀)],

где а₀ 0 — предельная величина адсорбции при стандартной температуре Т₀ (обычно принимают равной температуре тpoйной точки); a. — термический коэффициент предельной адсорбции, который можно вычислить по физическим константам адсорбата.

Температурная инвариантность характеристической кривой означает, что зависимость дифференциальной молярной работы адсорбции от степени заполнения q одна и та же для всех температур данной системы адсорбат—адсорбент. Термодинамически установлена нижняя граница строгого соблюдения температурной инвариантности q = 0,15. 0,20. При степени заполнения q 2 /b 2 )[lg(p_s/p)] 2 >, (7.8)

где В = 4,574/Ё 2 — константа.

Дальнейшее развитие ТОЗМ было направлено на область адсорбции газов при температурах Т > Т_к. Если химический потенциал адсорбтива в стандартном состоянии определятся некоторым параметром Z, а не давлением р, изменение энергии Ги66ca

В этом случае уравнение изотермы ТОЗМ имеет вид

При условии линейности изостер адсорбции в интервале температур Т Т_к, найдем параметр Z, определяющий стандартное состояние газа при Т > Т_к :

, (7.10)

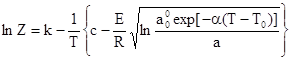
где k и с — константы уравнения изостеры адсорбции ln р = k — с/Т.

Полученные приближенные уравнения (7.9) и (7.10) позволяют рассчитать изотерму адсорбции вещества при наличии минимальной экспериментальной информации для o6ласти температур Т > Т_к (необходима только одна точка изотермы).

Последнее изменение этой страницы: 2019-03-22; Просмотров: 410; Нарушение авторского права страницы

Видео:5.1. Адсорбция. Классификация адсорбцииСкачать

Уравнение изотермы адсорбции в микропорах

Любые гетерогенные процессы, например, разложение или образование химического соединения, растворение твердых тел, газов или жидкостей, испарение, возгонка и т.п., а также многие другие процессы проходят в присутствии поверхностей раздела фаз (твердое тело — газ, твердое тело — жидкость, газ – жидкость). Состояние вещества у поверхности раздела соприкасающихся фаз отличается от его состояния внутри этих фаз вследствие различия молекулярных взаимодействий в разных фазах. Это различие вызывает особые поверхностные явления на границе раздела фаз.

Представим себе поверхность твердого тела на границе с газом. Внутри твердого тела частицы (атомы, ионы или молекулы), образующие его решетку, правильно чередуются в соответствии с кристаллической структурой, причем их взаимодействия уравновешены. Состояние же частицы, находящейся на поверхности, иное — взаимодействия таких частиц не уравновешены, и поэтому поверхность твердого тела притягивает молекулы вещества из соседней газовой фазы. В результате концентрация этого вещества на поверхности становится больше, чем в объеме газа, газ адсорбируется поверхностью твердого тела.

Таким образом, адсорбция представляет собой концентрирование вещества на поверхности раздела фаз. Вещество, на поверхности которого происходит адсорбция ‒ адсорбент , а поглощаемое из объемной фазы вещество — адсорбат .

Адсорбент поглощает из объемной фазы тем больше вещества, чем больше развита его поверхность. Поверхность, приходящаяся на 1 г адсорбента, называют удельной поверхностью. Величина удельной поверхности у различных адсорбентов может быть весьма различной. Непористые тела имеют удельную поверхность от нескольких м 2 /г до сотен м 2 /г. Большое увеличение поверхности связано обычно с наличием в твердом теле узких пор. Примерами таких высокодисперсных пористых тел с удельной поверхностью до нескольких тысяч м 2 /г являются активированный уголь и силикагель.

Количественно адсорбция может быть выражена с помощью нескольких величин:

величиною а, представляющей собой количество адсорбата, находящегося в объеме адсорбционного слоя, отвечающего единице массы адсорбента (моль/г).
величиною Г, представляющей собой избыток числа молей адсорбата в объеме поверхностного слоя площадью 1 см 2 по сравнению с числом его молей в том же объеме, если бы у межфазной границы не происходило изменение концентрации адсорбата (Г>0 — адсорбция, Г адсорбционного равновесия , аналогичное равновесию между испарением и конденсацией. Адсорбционное равновесие — это динимическое равновесие которое наступает тогда, когда скорость процесса адсорбции равна скорости обратного процесса десорбции. Понятно, что чем выше концентрация адсорбата, тем больше адсорбция. Также ясно, что чем выше температура, тем меньше физическая адсорбция. Для каждой температуры существует свое адсорбционное равновесие.

Адсорбцию принято характеризовать зависимостью количества адсорбированного вещества а от концентрации (или равновесного давления). Графики а=f(c) или а=f(р) при Т=const называют изотермами адсорбции . Вид обычной изотермы показан на рис.9.1.

Рисунок 9.1 ‒ Типичный вид изотермы адсорбции

Как можно видеть, изотерма имеет три характерных участка. Начальный круто поднимающийся вверх почти прямолинейный участок кривой показывает, что при малых концентрациях адсорбция пропорциональна концентрации. Это область, в которой выполняется закон Генри:[TEX]а=Кcdot[/TEX], где К – константа Генри, не зависящая от концентрации с. В области I поверхность адсорбента в значительной степени свободна.

Почти горизонтальный участок III соответствует большим концентрациям и отвечает поверхности адсорбента, полностью насыщенной адсорбатом. В. этих условиях, если на поверхности может образоваться лишь мономолекулярный слой адсорбата, количество его практически перестает зависеть от концентрации. Средний участок II кривой соответствует промежуточным степеням заполнения поверхности.

Важной задачей теории адсорбции является вывод уравнения изотермы адсорбции. В настоящее время эта задача еще далека от разрешения. Для описания изотермы адсорбции предложен ряд эмпирических формул. Из них наиболее широко используется уравнение Фрейндлиха :

где X — количество адсорбированного вещества, моль; m — масса адсорбента; с — равновесная концентрация, b и 1/n – константы.

Константы b и 1/n уравнения Фрейндлиха легко найти графически по изотерме, построенной в логарифмических координатах:

Это уравнение прямой. Тангенс угла наклона этой прямой равен 1/n, а отрезок, отсекаемый прямой на оси ординат, равен lnb. Константа b обычно колеблется в широких пределах. Физический смысл ее становится ясным, если принять с=1, тогда b представляет собой величину адсорбции при равновесной концентрации адсорбата 1 моль/л. Показатель 1/n принимается постоянным, лежащим в пределах 0,2 -1,0 для адсорбции из газовой среды и 0,1 — 0,5 для адсорбции из растворов. Поэтому уравнение Фрейндлиха пригодно лишь для концентраций, меньших 0,5 моль/л.2.

Видео:Построение изотермы адсорбцииСкачать

Мономолекулярная адсорбция. Изотерма адсорбции Ленгмюра

Фундаментальным вкладом в учение об адсорбции явилась теория Ленгмюра . Эта теория позволяет учесть наиболее сильные отклонения от закона Генри, связанные с ограниченностью поверхности адсорбента. Это обстоятельство приводит к адсорбционному насыщению поверхности адсорбента по мере увеличения концентрации адсорбируемого вещества. Это положение является основным в теории Ленгмюра и уточняется следующими допущениями:

адсорбция локализована на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата. На поверхности адсорбента образуется поэтому мономолекулярный слой адсорбата;
адсорбционные центры энергетически эквивалентны;
адсорбированные молекулы не взаимодействуют друг с другом.

Для вывода изотермы адсорбции Ленгмюра учтем, что при установлении в системе адсорбционного равновесия скорость адсорбции ([TEX]Vdownarrow [/TEX])должна равняться скорости десорбции( [TEX]Vuparrow [/TEX] ). Для того, чтобы молекула адсорбировалась, она должна удариться о поверхность и попасть на незанятое место. Учитывая, что число ударов пропорционально концентрации С, а вероятность попасть на незанятое место пропорционально их числу, имеем

где[TEX]Theta[/TEX]- доля занятых мест,[TEX]k_1[/TEX]- константа скорости адсорбции. Скорость десорбции прямо пропорциональна числу адсорбированных молекул:

где[TEX]k_2[/TEX]- константа скорости десорбции.

где[TEX] K=k_1/k_2[/TEX]- константа адсорбционного равновесия.

Обозначим символом[TEX]a_infty[/TEX]максимальную адсорбцию или емкость адсорбционного монослоя. Тогда

Это уравнение носит название изотермы адсорбции Ленгмюра. Для газов и паров концентрацию можно заменить пропорциональным ей значением давления и изотерма адсорбции примет вид

Константы адсорбционного равновесия К и[TEX]K_p[/TEX]характеризуют энергию взаимодействия адсорбата с адсорбентом. Чем сильнее это взаимодействие, тем больше значение константы адсорбционного равновесия.

Важны экстраполяционные следствия уравнения изотермы Ленгмюра. При[TEX]Crightarrow[/TEX]имеем[TEX]a=a_inftyKcdot[/TEX]и[TEX]Theta=Kcdot[/TEX].

Эти выражения соответствуют закону Генри: величина адсорбции линейно растет с увеличением концентрации. Таким образом уравнение Ленгмюра является более общим соотношением, включающим и уравнение Генри.

При больших концентрациях, когда[TEX] K_cgg1[/TEX]

Эти соотношения отвечают насыщению, когда вся поверхность адсорбента покрывается мономолекулярным слоем адсорбата. Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помощью уравнения Ленгмюра, записанного в линейной форме:

Методика нахождения коэффициентов уравнения Ленгмюра показана на рис. 9.2.

Рисунок 9.2 ‒ К нахождению констант уравнения Ленгмюра

Видео:Адсорбция на твёрдой поверхностиСкачать

Полимолекулярная адсорбция. Уравнение БЭТ

Опыт показывает, что наряду с изотермами адсорбции, которые описываются уравнением Ленгмюра и о которых мы говорили, часто встречаются изотермы, не имеющие участка, параллельного оси давлений и отвечающего насыщению поверхности адсорбента молекулами адсорбата. Такая изотерма — показана на рис 9.3. Это связано с явлением, при котором на активных центрах поверхности адсорбента образуются несколько слоев молекул или ионов адсорбата — полимолекулярная адсорбция .

Наиболее удачная теория (из многочисленных), описывающая подобные процессы была создана в 1935-1940 гг. Брунауэром, Эмметом, Теллером применительно к адсорбции паров. Их теория получила название теории БЭТ. Ее основные положения:

Адсорбционные слои полимолекулярны, причем их толщина на разных участках поверхности различна.
Адсорбционные силы тождественны силам, вызывающим конденсацию.

Рисунок 9.3 ‒ Изотерма полимолекулярной адсорбции

Последнее положение может быть обосновано следующим образом: лишь первый слой молекул адсорбата находится в непосредственной близости к поверхности твердого тела. Второй, и особенно последующие слои, прилегают к молекулам, подобным им, и их образование напоминает обычную конденсацию пара на поверхности жидкости.

На основании этих представлений Брунауэр, Эммет и Теллер вывели следующее уравнение изотермы адсорбции паров:

где[TEX]K_П[/TEX]- константа равновесия полимолекулярной адсорбции, Р — давление пара, [TEX]P_s[/TEX] — давление насыщенного пара при данной температуре,[TEX]a_infty[/TEX]- емкость монослоя.

При низких давлениях, когда[TEX]p/p_sll 1[/TEX], учитывая, что[TEX]K_p=K_Пcdot[/TEX], получаем уравнение Ленгмюра:

Уравнение изотермы полимолекулярной адсорбции БЭТ легко привести к линейной форме:

По наклону этой прямой и отсекаемому ею отрезку на оси ординат можно найти значения констант[TEX]a_infty[/TEX]и[TEX]K_П[/TEX].

Теория БЭТ, так же как и теория Ленгмюра, указывает путь для определения удельной поверхности адсорбента (любого твердого вещества). Для этого находят емкость монослоя [TEX]a_infty[/TEX] для паров простых веществ ( [TEX]N_2[/TEX] , Ar, Kr) при низких температурах. Затем, зная площадь [TEX]S_0[/TEX] , занимаемую одной молекулой простого вещества, вычисляют удельную поверхность адсорбента:

где [TEX]N_a[/TEX] — число Авогадро. Это метод определения удельной поверхности по БЭТ.

Видео:Адсорбция на поверхностях растворовСкачать

Энергетические параметры адсорбции на однородной поверхности

Между энергией Гиббса, энтальпией и энтропией адсорбции существует известное соотношение:

Адсорбция — самопроизвольный процесс, а всякому самопроизвольному процессу при P,T=const отвечает условие [TEX]Delta . Энтропия также уменьшается ([TEX]Delta ~~[TEX]Delta . Таким образом, адсорбция — экзотермический процесс.~~

Если адсорбция подчиняется уравнениям Генри и Ленгмюра, т.е. константа равновесия адсорбции в этих уравнениях не зависят от степени заполнения поверхности, то стандартная энергия Гиббса адсорбции может быть рассчитана по уравнению, справедливому для химических реакций:

Энтальпию адсорбции определяют из экспериментальной зависимости константы равновесия адсорбции от температуры в соответствии с уравнением изобары Вант-Гоффа

~~Принимая во внимание слабую зависимость изменения энтальпии от температуры, находим~~

~~Тангенс угла наклона прямой lnK — 1/T равен -[TEX]Delta/R[/TEX], откуда легко рассчитать[TEX]Delta[/TEX].~~

Энтропию адсорбции, подчиняющейся закону Генри или уравнению Ленгмюра, легко рассчитать, если известны [TEX]Delta[/TEX] и [TEX]Delta[/TEX] по уравнению

Данные соотношения для расчета энергетических параметров адсорбции получены, исходя из предположения, что поверхность адсорбента однородна (эквипотенциальна) и на ней образуется мономолекулярный слой адсорбата.

Если адсорбция происходит на неоднородной поверхности, то наиболее реакционноспособные адсорбционные центры будут заняты уже при малых равновесных концентрациях. Таким образом, энергетические параметры адсорбции зависят от степени заполнения поверхности адсорбатом. Например, дифференциальная теплота адсорбции будет уменьшаться по мере заполнения поверхности.

~~Видео:Поверхностные явления. Адсорбция на подвижных границах раздела фаз.Скачать~~

Взаимодействие частиц в адсорбционном слое и классификация изотерм адсорбции

Одним из опорных пунктов теории Ленгмюра является константа отсутствия взаимодействия частиц адсорбата в адсорбционном слое, Однако ленгмюровская адсорбция является лишь частным случаем в многообразном мире адсорбционных процессов. На рис. 9.4 показаны различные формы изотерм адсорбции из разбавленных растворов.

~~Рисунок 9.4 ‒ Формы изотерм адсорбции~~

Исходя из формы начального участка были выделены четыре характерных класса изотерм (S, L, H, C). Деление изотерм на отдельные типы внутри каждого класса связано с последующим изменением их формы при наиболее высоких концентрациях. Класс L (класс Ленгмюра) является наиболее общим. Изотермы типа L2 достигают насыщения, дальнейшая адсорбция выше этого уровня дает изотерму типа L3. Если достигается второе плато, то имеем дело с изотермой L4. Для изотерм типа L5 характерно наличие максимума. Максимум отражает изменение состояния вещества в растворе — например, ассоциацию молекул при определенной концентрации. Сходный, хотя и не столь полный, набор типов изотерм получен и для других классов.

Начальный участок изотерм S — класса выгнут относительно оси концентраций, однако далее часто следует точка перегиба, что и придает изотерме характерную S -обратную форму.

Изотермы класса Н (высокое сродство – higf) наблюдается при чрезвычайно сильной адсорбции при очень низких концентрациях; они пересекаются с осью ординат. Изотермы класса С (constant) имеют начальный линейный участок, что указывает на постоянное распределение растворенного вещества между раствором и адсорбентом (постоянная скорость адсорбции).

Теоретический анализ различных типов изотерм адсорбции позволяет получить много полезной информации о механизме адсорбции. При этом следует принимать во внимание величину энергии активации процесса удаления молекул адсорбата с поверхности адсорбента. Если взаимодействие между адсорбированными молекулами пренебрежимо мало, энергия активации не зависит от степени заполнения поверхности_f a это приведет к изотерме типа L или Н.

Если сила взаимодействия между адсорбированными молекулами больше силы взаимодействия между растворенным веществом и адсорбентом, энергия активации возрастает и адсорбция описывается изотермой типа S. В этом случае молекулы растворенного вещества стремятся расположиться на поверхности в виде цепей.

~~Изотермы типа Н наблюдаются в тех случаях, когда имеет место хемосорбция.~~

Изотерма типа С характерна для адсорбции на микропористых адсорбентах и соответствует таким условиям, при которых число адсорбционных центров остается постоянным в широкой области концентраций. По мере заполнения одних центров появляются новые, и доступная для адсорбции поверхность увеличивается пропорционально количеству адсорбированного вещества.