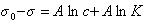Уравнение изотермы адсорбции гиббса поверхностная активность (2 видео)

УРАВНЕНИЕ АДСОРБЦИИ ГИББСА

Выше (п. 2.4) мы пришли к выводу, что процесс адсорбции обусловлен снижением поверхностного натяжения. Очевидно, чем в большей степени ПАВ снижает поверхностное натяжение, тем большей должна быть его адсорбция. Напротив, ПИВ должна быть присуща отрицательная адсорбция.

Исходя из второго закона термодинамики американский ученый Дж. Гиббс в 70–х гг. XIX в. вывел важное уравнение, связывающее величину адсорбции со способностью растворенного вещества изменять поверхностное натяжение раствора:

(3.1)

где Г_i, – избыточная адсорбция i-го компонента (см. 2.10), c_i – его молярная концентрация в растворе, Т – температура, при которой происходит адсорбция, R – газовая постоянная, – изменение поверхностного натяжения раствора при изменении концентрации на dc_i.

В такой форме уравнение Гиббса применяется для разбавленных растворов. Вы, очевидно, помните, что для концентрированных растворов концентрацию нужно заменить активностью:

(3.2)

Уравнение Гиббса было выведено теоретически. В дальнейшем оно было подтверждено экспериментально Мак–Беном методом среза тонких слоев с последующим их химическим анализом. Аналогичные исследования были проведены Сазаки с использованием метода радиоактивных индикаторов.

Проанализируем уравнение Гиббса.

Если 0, т. е. наблюдается положительная избыточная адсорбция – i–е вещество концентрируется на поверхности раствора; если >0, то Г_i

Рис. 3.2. Определение избыточной адсорбции

Рис. 3.3. Изотерма адсорбции

Значение избыточной адсорбции для любой концентрации

с_i		Z_i	Г_i	с_i		Z_i	Г_i
c₁	₁	Z₁	Г₁	c₄	₄	Z₄	Г₄
c₂	₂	Z₂	Г₂	…	…	…	…
c₃	₃	Z₃	Г₃	…	…	…	…

ПОВЕРХНОСТНАЯ АКТИВНОСТЬ.

ПРАВИЛО ДЮКЛО-ТРАУБЕ

Из уравнения Гиббса следует, что характеристикой поведения вещества при адсорбции является величина производной , однако ее значение изменяется при изменении концентрации (см. рис. 3.2). Чтобы придать этой величине вид характеристической постоянной, берут ее предельное значение (при с 0). Эту величину П. А. Ребиндер (1924) назвал поверхностной активностью g:

(3.4)

[g] = Дж–м 3 /м 2 -моль = Дж–м/моль или Н-м 2 /моль.

Чем в большей степени уменьшается поверхностное натяжение с увеличением концентрации адсорбируемого вещества, тем больше поверхностная активность этого вещества, и тем больше его гиббсовская адсорбция.

Поверхностную активность можно определить графически как отрицательное значение тангенса угла наклона касательной, проведенной к кривой =f(c) в точке ее пересечения с осью ординат.

Таким образом, для ПАВ: g > 0; 0. Для ПИВ: g 0, Г_i

2. В гомологическом ряду прослеживаются четкие закономерности в изменении поверхностной активности (g): она возрастает по мере увеличения длины углеводородного радикала.

На основании большого экспериментального материала в конце XIX в. Дюкло и Траубе сформулировали правило:

Поверхностная активность предельных жирных кислот в водных растворах возрастает в 3–3,5 раза при удлинении углеводородной цепи на одно звено (группу –CH₂).

На рис. 3.4 приведены изотермы поверхностного натяжения для ряда кислот.

Рис.3.4. Изотерма поверхностного натяжения некоторых кислот

1 – СН₃СООН – уксусная кислота (n_с=1); 2 – СН₃СН₂СООН – пропионовая кислота (n_с =2); 3 – СН₃(СН₂)₂СООН – масляная кислота (n_с =3); 4 – СН₃(СН₂)₃СООН – изовалериановая кислота (n_с = 4); 5 – СН₃(СН₂)₄СООН – капроновая кислота (n_с =5); n_с – число атомтов С в углеводородном радикале.

Рис. 3.6 Ориентация молекул ПАВ на поверхности водного раствора

а – при малых концентрациях; б – при умеренных концентрациях; в – в насыщенном адсорбционном слое.

При малых концентрациях углеводородные цепи, вытолкнутые в воздух, «плавают» на поверхности воды, тогда как полярная группа погружена в воду (рис. 3.6а), такое положение возможно из-за гибкости углеродной цепи. С ростом концентрации число молекул в поверхностном слое увеличивается, цепи поднимаются. Какие-то из них принимают вертикальное положение (рис. 3.6б). В насыщенном адсорбционном слое поверхность воды оказывается сплошь покрытой «частоколом» из вертикально ориентированных молекул ПАВ (рис. 3.6в), значение поверхностного натяжения в этом случае приближается к значению, характерному для чистого жидкого ПАВ на границе с воздухом.

Из-за вертикальной ориентации молекул ПАВ в поверхностном слое максимальная адсорбция ( ) не зависит от длины «хвоста» (углеводородного радикала), а определяется только размерами поперечного сечения молекулы, которые в гомологическом ряду остаются неизменными.

Экспериментально найденная величина дает возможность рассчитать поперечный размер молекулы (S_o).

Предельная избыточная адсорбция ПАВ равна:

(3.5)

где – количество ПАВ в поверхностном слое. Так как поверхностный слой полностью заполнен молекулами ПАВ,

(3.6)

где N_a — число Авогадро.

Подставляя полученное значение S_1,2 в уравнение (3.5), получаем

или (3.7)

Так было найдено, что поперечный размер S_o молекул всех жирных кислот равен 20 * 10 -16 см 2 , а предельных спиртов – 25 * 10 -16 см 2 . Из величины предельной адсорбции была найдена также длина молекулы .

Масса 1 см 2 поверхностного слоя равна

, (3.8)

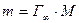
где М – молярная масса ПАВ.

В то же время плотность

, (3.9)

так как объем 1 см 3 поверхностного слоя равен . Из формул (3.8) и (3.9) следует:

(3.10)

Экспериментальные данные показали, что длина молекулы ПАВ пропорциональна числу атомов углерода в углеводородном радикале n_с, и нм для всего ряда. Величина 0,13 нм близка к диаметру атома углерода.

Таким образом, размеры молекул впервые в истории химии были определены коллоидно-химическим методом. В дальнейшем эти результаты были подтверждены другими методами.

УРАВНЕНИЕ ШИШКОВСКОГО

В 1908 г. киевский ученый Б. А. Шишковский эмпирическим путем получил уравнение, связывающее поверхностное натяжение водных растворов ПАВ с их концентрацией:

(3.11)

где – поверхностное натяжение воды; – поверхностное натяжение раствора; с – концентрация раствора; В – константа, мало зависящая от природы ПАВ внутри данного гомологического ряда; К – удельная капиллярная постоянная, которая увеличивается в 3–3,5 раза при удлинении углеводородного радикала на одно звено (группу –СН₂–).

Для того чтобы выяснить физический смысл постоянной В, обратимся к.уравнению Гиббса:

или

Разделим переменные и примем, что

Интегрируем это уравнение, принимая во внимание, что . – величина постоянная:

(3.12)

где А – постоянная интегрирования.

Уравнение (3.12) получено в результате преобразования уравнения Гиббса для предельной адсорбции. Теперь для этих же условий запишем уравнение Шишковского, принимая во внимание, что максимальная адсорбция может быть достигнута при достаточно больших концентрациях ПАВ.

Тогда с >> 1, Кс >> 1 и 1 + Кс Кс и

(3.13)

Сравнивая уравнения (3.13) и (3.12), видим, что

(3.14)

Теперь становится понятным, почему величина В в уравнении Шишковского остается постоянной в пределах одного гомологического ряда.

Однако смысл удельной капиллярной постоянной К пока остается неясным

ТЕОРИЯ МОНОМОЛЕКУЛЯРНОЙ

АДСОРБЦИИ ЛЕНГМЮРА

Отметим основные положения этой теории.

1. Адсорбция мономолекулярна.

2. При адсорбции устанавливается динамическое равновесие, которое можно рассматривать как квазихимическое. В условиях равновесия скорости процессов адсорбции и десорбции равны.

Константа адсорбционного равновесия

где к_адс – константа скорости адсорбции; к_дес – константа скорости десорбции.

Исходя из данной теории было выведено уравнение, которое мы приводим без вывода:

(3.15)

где – максимальная адсорбция ПАВ; Г – адсорбция при концентрации с; К – константа адсорбционного равновесия.

Зависимость величины адсорбции от концентрации представлена на рис.3.7.

На кривой четко видны три участка:

I участок – прямая линия, выходящая из начала координат. Действительно, из уравнения Ленгмюра (3.15) при малых концентрациях Кс > 1 и 1 + Кс Кс. Следовательно,

II участок – соответствует криволинейной части графика и описывается полным eравнением Ленгмюра (3.15).

Рис.3.7. Зависимость адсорбции от концентрации ПАВ.

Чтобы найти постоянные в уравнении Ленгмюра, его следует привести к линейной форме. Для этого правую и левую части уравнения надо «перевернуть»:

(3.16)

Умножим обе части уравнения (3.16) на с:

(3.16)

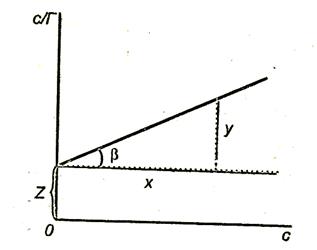
На рис. 3.8. показан график .

Тангенс угла наклона прямой к оси абсцисс

Отрезок, отсекаемый прямой на оси ординат,

Рис.3.8. Зависимость величины с/Г от концентрации ПАВ.

Доказано, что К в уравнении Шишковского (удельная капиллярная постоянная) и К в уравнении Ленгмюра (константа адсорбционного равновесия) – это одна и та же величина.

Построив график , можно найти предельную адсорбцию и константу адсорбционного равновесия К.

Так как адсорбция рассматривается как псевдохимическая реакция, на основе химической термодинамики можно записать

(3.18)

где А_m_ах – работа адсорбции.

Шишковский эмпирическим путем установил, что константа К увеличивается в 3–3,5 раза при удлинении цепи на одно звено –СН₂.

Напишем выражение для разности работ адсорбции двух соседних членов гомологического ряда.

= 8,31 * 298 * In 3,5 3,2 кДж/моль,

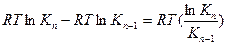
где n – число атомов углерода в углеводородном радикале.

Это означает, что для перевода каждой –СН₂–группы из поверхностного слоя в объемную фазу надо затратить 3,2 кДж/моль энергии. Это работа раздвижения диполей воды на величину объема –СН₂–группы – величина аддитивная и одинаковая для различных рядов алифатических предельных соединений. Постоянная разность работ адсорбции для двух соседних членов превращается в постоянное отношение (3–3,5), фигурирующее в правиле Дюкло–Траубе. Сущность этого правила, таким образом, заключается в том, что работа адсорбции на каждую –СН₂–группу является постоянной, близкой к 3,5 кДж/молъ.

В заключение отметим, что помимо уравнения Гиббса, Шишковского и Ленгмюра существует уравнение Фрумкина, позволяющее рассчитать изменение поверхностного натяжения в результате адсорбции:

(3.19)

ЗАКЛЮЧЕНИЕ

Адсорбция поверхностно-активных веществ (ПАВ) на поверхности «жидкий раствор–газ» – самопроизвольный процесс, обусловленный уменьшением поверхностного натяжения. Для поверхностно-инактивных веществ (ПИВ), повышающих поверхностное натяжение, характерна отрицательная адсорбция.

Основным уравнением адсорбции является уравнение Гиббса, связывающее величину избыточной адсорбции с концентрацией ПАВ и его поверхностной активностью. Кривая, выражающая зависимость поверхностного натяжения от концентрации ПАВ при постоянной температуре, называется изотермой поверхностного натяжения. Тангенс угла наклона к оси абсцисс касательной к изотерме поверхностного натяжения при с 0 позволяет определить поверхностную активность. Аналитическим выражением изотермы поверхностного натяжения является уравнение Шишковского, выведенное на основе экспериментальных данных. Если известны постоянные этого уравнения и поверхностное натяжение растворителя, можно рассчитать поверхностное натяжение раствора заданной концентрации.

Поверхностная активность ПАВ, согласно теории Ленгмюра, обусловлена дифильным строением их молекул: полярные группы втягиваются в глубь фазы, а неполярные углеводородные части выталкиваются в неполярную среду (воздух, газ), снижая тем самым поверхностное натяжение. С увеличением углеродной цепи на одну –СН₂–группу поверхностная активность увеличивается в 3-3,5 раза (правило Дюкло–Траубе). Исходя из теории Ленгмюра, были впервые рассчитаны площадь, занимаемая одной молекулой, и длина молекулы ПАВ.

Зависимость величины адсорбции ПАВ от концентрации выражается уравнением Ленгмюра, выведенным исходя из представлений о скоростях процессов адсорбции и десорбции. Соответствующий график Г = f(с) называется изотермой Ленгмюра.

Изменение поверхностного натяжения в зависимости от адсорбции рассчитываются по уравнению Фрумкина.

ВОПРОСЫ И ЗАДАЧИ ДЛЯ САМОКОНТРОЛЯ

1. Какие вещества называются поверхностно-активными, поверхностно-инактивными?

2. В чем состоят особенности строения молекул ПАВ и ПИВ и их адсорбции?

3. Как зависит поверхностное натяжение от концентрации ПАВ в растворе?

4. Что называется поверхностной активностью? Как ее можно определить графически и аналитически?

5. В чем заключается правило Дюкло–Траубе?

6. Как графически и аналитически можно определить предельную адсорбцию?

7. Как рассчитать площадь, занимаемую молекулой, и толщину поверхностного слоя?

8. Для водных растворов изоамилового спирта константы уравнения Шишковского: В = 21,12 * 1СГ 3 Дж/м 2 ; К = 42,0 м 3 /кмоль. Поверхностное натяжение чистой воды при заданной температуре равно 72,9 * 10 -3 Дж/м 2 :

а) определите поверхностное натяжение растворов концентраций: 0,012; 0,016; … 0,032 кмоль/м 3 ,

б) постройте изотерму поверхностного натяжения,

в) определите графически поверхностную активность спирта,

г) по уравнению Гиббса вычислите адсорбцию спирта для заданных в п. а) концентраций,

д) постройте изотерму адсорбции и определите графи чески предельную адсорбцию,

е) определите площадь, занимаемую одной молекулой спирта в поверхностном слое.

9. Сравните поверхностную активность этанола и н-бутанола в водных растворах одинаковой концентрации.

10 Изотерма адсорбции ПАВ описывается уравнением Ленгмюра Г=Г_m_ах*(Кс/(1 + Кс)). Найдите графическим методом константы Г_m_ах и К.

11. Предельная адсорбция пропионовой кислоты равна 4,18 * 10 -6 моль/м 2 . Рассчитайте значение константы В в уравнении Шишковского, при стандартной температуре.

Закончив изучение главы 3, вы должны

1. понятия «поверхностно–активные» и «поверхностно-инактивные» вещества, «поверхностная активность»;

2. от чего зависит поверхностная активность ПАВ;

3. сущность теории мономолекулярной адсорбции Ленгмюра;

4. уравнения Гиббса, Шишковского, Ленгмюра, Фрумкина, какие зависимости каждое из них выражает;

1. строить изотерму поверхностного натяжения и определять графически поверхностную активность;

2. рассчитывать поверхностную активность по уравнению Гиббса;

3. рассчитывать поверхностное натяжение по уравнению Шишковского;

4. строить изотерму гиббсовской адсорбции и определять предельную адсорбцию ПАВ;

5. исходя из предельной адсорбции рассчитывать поперечный размер So и длину молекул .

Содержание

1.5. Поверхностное натяжение растворов и адсорбция
Реферат: Адсорбция и адсорбционные равновесия
Адсорбция
Фундаментальное уравнение Гиббса. Определение Гиббсовской адсорбции. Адсорбционное уравнение Гиббса
Поверхностная активность. Поверхностно-активные и поверхностно-инактивные вещества. Анализ уравнения Гиббса. ПАВ. Эффект Ребиндера. Правило Дюкло-Траубе
🔍 Видео

Видео:5.1. Адсорбция. Классификация адсорбцииСкачать

1.5. Поверхностное натяжение растворов и адсорбция

Свободная поверхностная энергия самопроизвольно может только уменьшаться, что проявляется в уменьшении либо поверхности раздела фаз, либо межфазного (поверхностного) натяжения. Поверхностное натяжение может уменьшаться в результате самопроизвольного перераспределения компонентов системы между объемами фаз a и b и поверхностью их раздела. В поверхности раздела фаз будут преимущественно концентрироваться те компоненты, которые способны уменьшать избыточную свободную поверхностную энергию. Это явление получило название «адсорбция». Количественно мерой адсорбции служит избыток вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же слое в объеме фазы. Этот избыток обычно относят к единице площади поверхности (или к единице массы адсорбента). Такая адсорбция называется гиббсовской и обозначается буквой Г_i. Поверхностный избыток является алгебраической величиной. Если он положителен, то вблизи поверхности данный компонент присутствует в избытке, если отрицателен, то концентрация компонента на поверхности фазы ниже, чем в ее объеме .

Рассмотрим распределение в системе i -го компонента, предполагая, что это вещество способно понижать поверхностное натяжение. В соответствии с уравнением (1.1.6) число молей n вещества i-го компонента в системе определяется как .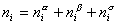

Количество вещества в обеих фазах составляет

. (1.1.81)

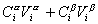
где С a , С b — концентрация вещества в фазах a, b.

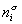
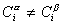
Количество вещества на поверхности раздела фаз , избыточное по отношению к объемам фаз V a и V b , оказывается зависимым от положения разделяющей плоскости, так как концентрации вещества в различных фазах не равны, .

Учитывая уравнение (1.1.81) ,

. (1.1.82)

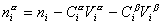
Разделив выражение (1.1.82) на площадь поверхности раздела фаз А, можем определить гиббсовскую адсорбцию:

. (1.1.83)

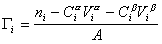
Фундаментальным уравнением физической химии поверхностей является взаимосвязь между адсорбцией и межфазным натяжением, которую можно определить экспериментально при одновременном изменении многих факторов. Остановимся на системах, в которых адсорбция протекает при постоянной температуре. Связь между адсорбцией и межфазным натяжением при постоянной температуре T называется изотермой адсорбции, фундаментальное уравнение которой известно как уравнение Гиббса. Рассмотрим его вывод.

При небольшом обратимом изменении энергии системы dU с учетом формулы (1.1.4) можем написать

, (1.1.84)

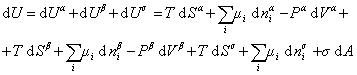
где U – полная внутренняя энергия системы; U a , U b , U s – внутренняя энергия фаз aиb и поверхности их раздела; P a , P b — давление в фазах aиb; m — химический потенциалi-того компонента; S a , S b , S s – энтропия фаз a иb и их поверхности раздела; s — поверхностное натяжение.

Поскольку из курса химической термодинамики известно, что

(1.1.85)

, (1.1.86)

. (1.1.87)

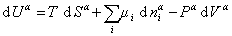
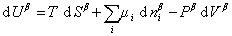
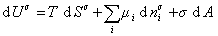
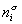
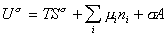
Если энергию, энтропию и количество компонентов увеличивать от нуля до некоторого определенного значения при постоянстве температуры T, площади поверхности раздела фаз A и количестве вещества на этой поверхности , то уравнение (1.1.87) переходит в общее уравнение

, (1.1.88)

дифференцирование которого приводит к выражению

. (1.1.89)

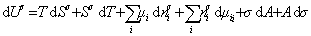
Сравнивая его с уравнением (1.1.88), получаем

. (1.1.90)

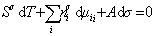
В расчете на единицу поверхности

, (1.1.91)

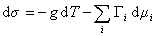
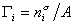
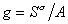
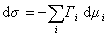
где – гиббсовская адсорбция; – удельная энтропия поверхностного слоя.

. (1.1.92)

Для двухкомпонентной системы

, (1.1.93)

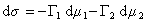
где индекс 1 относится к растворителю, а индекс 2 – к растворенному веществу.

Рис. 1.15. Схема реальной (I) межфазовой области и идеальной (II) и (III) разделяющей межфазовой поверхности (поверхности Гиббса)

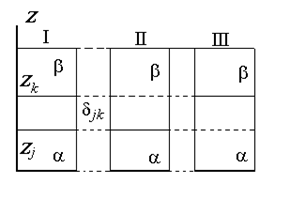
Разделяющая поверхность Гиббса может быть проведена так, чтобы обратилась в нуль адсорбция любого наперед заданного компонента, но только одного, как это показано на рис. 1.15.

Расстояние между двумя плоскостями (разделяющими поверхностями), одна из которых соответствует условию Г_j = 0, а другая — Г_k = 0, обозначим d_kj:

, (1.1.94)

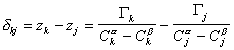
где Г_k, Г_j– избытки рассматриваемых компонентов в поверхностном слое ; C_k a , C_k b , C_j a , C_j b – концентрация компонентов k и j в фазах a и b; z_k, z_j – координаты разделяющей поверхности.

Поскольку значения Г₁ в уравнении (1.1.93) определены относительно произвольно выбранного положения разделяющей плоскости, то ее можно расположить так, чтобы избыток растворителя в поверхностном слое был равен нулю ( Г₁ = 0).

, (1.1.95)

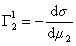
где верхний индекс 1 означает, что для выбранной поверхности раздела Г₁=0.

, (1.1.96)

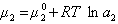
получаем после дифференцирования уравнения (1.1.96)

, (1.1.97)

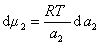
где 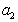— активность растворенного вещества.

Поэтому, подставляя уравнение (1.1.97) в уравнение (1.1.95), получаем

. (1.1.98)

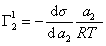
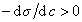
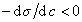
Из уравнения (1.1.98) следует, что если , то адсорбция положительна, а при возникает дефицит растворенного вещества на разделяющей поверхности .

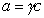
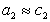
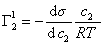
Поскольку , где g – коэффициент активности, который для разбавленных растворов стремится к единице, то и

. (1.1.99)

Уравнение (1.1.99) представляет собой наиболее употребляемую форму изотермы адсорбции Гиббса, причем так как рассматривается адсорбция именно растворенного вещества, индексы при адсорбции и концентрации опускают, т.е.

. (1.1.100)

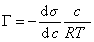
Исследования показывают, что существуют такие вещества, растворение которых приводит к резкому снижению поверхностного натяжения раствора. Эти вещества называют поверхностно-активными. В соответствии с уравнением Гиббса адсорбция их всегда положительна, т.е. концентрация в поверхностном слое выше объемной концентрации. По предложению Ребиндера мера поверхностной активности обозначается первой буквой фамилии Гиббса. Обычно используют значения поверхностной активности в бесконечно разбавленных растворах

. (1.1.101)

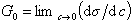
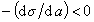
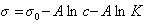
К классу поверхностно-активных веществ (ПАВ) относятся жирные кислоты и их соли (мыла), сульфокислоты, их соли, спирты, алкилсульфоэфиры и др. Если , то Г >1, то единицей в уравнении Шишковского (1.1.105 ) можно пренебречь, тогда

. (1.1.106)

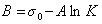
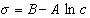
Обозначим постоянной В постоянные при изотермических условиях величины , тогда

. (1.1.107)

Следовательно, при относительно высокой концентрации растворов ПАВ их поверхностное натяжение должно уменьшаться экспоненциально с увеличением концентрации.

Уравнение (1.1.107) может быть получено непосредственно из уравнения изотермы адсорбции Гиббса:

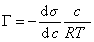
При достаточно высокой концентрации растворенного вещества адсорбция достигает предела , т.е. Г = Г_max , поэтому

, (1.1.108)

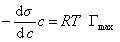
где при постоянной температуре правая часть представляет собой постоянную величину и может быть обозначена RT Г_max = A. Следовательно,

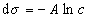
откуда после интегрирования получаем

. (1.1.109)

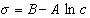
Таким образом, уравнение Шишковского может быть выведено из уравнения Гиббса, так как уравнения (1.1.107) и (1.1.109) идентичны. Точность уравнения Шишковского связана с тем, что в нем уже заложено условие насыщения адсорбционного слоя.

Если уравнение Шишковского в форме

(1.1.110)

, (1.1.111)

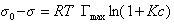
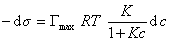
и подставить в уравнение Гиббса величину

, (1.1.112)

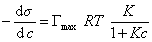
то уравнение изотермы адсорбции примет вид

. (1.1.113)

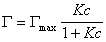
В такой форме уравнение изотермы адсорбции носит название изотермы Ленгмюра. Американский ученый И. Ленгмюр в 1917 г. развил представление о мономолекулярной адсорбции и на основании молекулярно- кинетической теории получил уравнение (1.1.113) .

Уравнение Шишковского позволяет определить предел адсорбции (при Kc>>1), так как в таком случае это уравнение принимает вид

. (1.1.114)

Рис. 1.16. Зависимость поверхностного натяжения от концентрации растворов ПАВ в координатах уравнения Шишковского

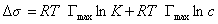
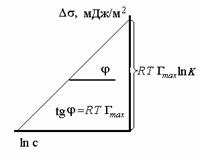
Построив график 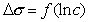, как это показано на рис. 1.16, по углу наклона можно определить предел адсорбции, а по отрезку, отсекаемому наклонной линией на оси ординат при ln c = 0, рассчитать постоянную равновесия процесса адсорбции K.

Понимание адсорбционных процессов имеет чрезвычайно важное значение, так как они лежат в основе многих процессов, протекающих на границе раздела фаз, например крашения, отмывания загрязнений, отделки текстильных материалов и т.д., т.е. в основе всех коллоидно -химических процессов на границе жидкость–газ.

Видео:Поверхностные явления. Адсорбция.Скачать

Реферат: Адсорбция и адсорбционные равновесия

Видео:Адсорбция на поверхностях растворовСкачать

Адсорбция

Понятие адсорбции. Автоадсорбция. Адсорбент и адсорбат. Абсолютная и Гиббсовская адсорбция. Единицы измерения адсорбции. Зависимость величины адсорбции от концентрации, давления и температуры. Изотерма, изобара, изопикна, изостера адсорбции

Адсорбция — процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемом фазы.

Адсорбция может наблюдаться в многокомпонентных системах и при перераспределении в поверхностный слой уходит тот компонент, который сильнее понижает поверхностное натяжение. В однокомпонентной системе при формировании поверхностного слоя происходит изменение его структуры — уплотнение, которое называется автоадсорбцией .

В общем случае адсорбция может происходить не только благодаря стремлению поверхностной энергии к уменьшению, но и за счет химической реакции компонентов с поверхностью вещества. В этом случае поверхностная энергия может даже увеличиваться на фоне снижения энергии всей системы.

Вещество, на поверхности которого происходит адсорбция, называется адсорбентом , а вещество, которое перераспределяется – адсорбатом .

Обратный процесс перехода вещества с поверхности в объем фазы — десорбция.

В зависимости от агрегатного состояния фаз различают адсорбцию газа на твердых адсорбентах, твердое тело – жидкость, жидкость — жидкость, жидкость — газ. Для количественного описания адсорбции применяют две величины: первая измеряется числом молей или граммами, приходящимися на единицу поверхности или массы адсорбента:

Величина, определяемая избытком вещества в поверхностном слое, также отнесенным к единице площади поверхности или массы адсорбента, называется Гиббсовской или относительной адсорбцией (Г).

Адсорбция зависит от концентрации компонентов и температуры.

Различают следующие виды зависимостей:

Название: Адсорбция и адсорбционные равновесия
Раздел: Рефераты по химии
Тип: реферат Добавлен 16:01:44 27 января 2009 Похожие работы
Просмотров: 6813 Комментариев: 24 Оценило: 7 человек Средний балл: 4.3 Оценка: 4 Скачать

1. Изотерма (рис. 8)	2. Изобара	3. Изостера
А =f_T (c)	А =f_P (T)	c=f_A (T)
A=f_T (P)	A=f_C (T)	P=f_A (T)

Видео:Поверхностные явления. Адсорбция на подвижных границах раздела фаз.Скачать

Фундаментальное уравнение Гиббса. Определение Гиббсовской адсорбции. Адсорбционное уравнение Гиббса

Считаем V _{поверхности раздела} = 0.

dU = TdS + s dS +

Проинтегрировав, получим: U = TS + sS +

Полный дифференциал от этого уравнения:

dU = TdS + SdT + s dS + + Sd s + .

Подставляя значение dU из (6) в (7) и сократив одинаковые члены правой и левой части, получим:

SdT + Sd s + = 0.

Предположим, что T = const:

Разделив правую и левую часть на поверхность S , получим фундаментальное адсорбционное уравнение Гиббса :

; ;

Определение зависимости поверхностного натяжения от адсорбции одного компонента, при постоянстве химических потенциалов других компонентов.

Известно, что , , (где , — равновесный и стандартный химический потенциал компонента i ; lna_i — логарифм активности i –го компонента). Тогда уравнение Гиббса будет выглядеть так

Активность связана с концентрацией: с =  × а . Предположим, что  = 1 (при с ® 0). Тогда

— для жидкости и газа

Обычно уравнение Гиббса применяют для растворов. Растворителем может быть не только индивидуальное вещество, но и смесь. В разбавленных растворах гиббсовская адсорбция очень мала, а его химический потенциал меняется очень мало с изменением концентрации растворенного вещества, т.е. d m= 0. Поэтому для разбавленного раствора фундаментальное уравнение Гиббса выглядит так:

Из этих уравнений следует, что зная зависимость = f (С) (где С — концентрация растворенного вещества), можно рассчитать изотерму адсорбции, пользуясь адсорбционным уравнением Гиббса. Схема графического расчета показана на рис. 2.2.2.1: Тангенс угла наклона соответствует значениям производных в этих точках.

Зная эти производныеуравнения Гиббса, можно рассчитать значение Г , что позволяет построить зависимость Г = f (С) . Уравнение Гиббса показывает, что единица измерения гиббсовской адсорбции не зависит от единицы измерений концентрации, а зависит от размерности величины R . Так как величина R отнесена к молю вещества, а s — к единице площади, то Г = [моль/ единица площади]. Если s выразить в [Дж/м 2 ], то R нужно подставлять: R = 8,314 Дж/моль×К.

Видео:Поверхностные явленияСкачать

Поверхностная активность. Поверхностно-активные и поверхностно-инактивные вещества. Анализ уравнения Гиббса. ПАВ. Эффект Ребиндера. Правило Дюкло-Траубе

В уравнении Гиббса влияние природы вещества на адсорбцию отражается производной. Эта производная определяет и знак гиббсовской адсорбции, и может служить характеристикой вещества при адсорбции. Чтобы исключить влияние концентрации на производную берут ее предельные значения, т.е. при стремлении концентрации к нулю. Эту величину Ребиндер назвал поверхностной активностью .

;

g = [Дж×м/моль] = [Н×м 2 /моль]; [эрг см/моль] = [Гиббс].

Уравнение показывает, что чем сильнее снижается = f ( c ) с увеличением концентрации, тем больше поверхностная активность этого вещества.

Физический смысл поверхностной активности состоит в том, что она представляет силу, удерживающую вещество на поверхности и отнесенную к единице гиббсовской адсорбции .

Поверхностную активность можно представить как отрицательный тангенс угла наклона к касательной, проведенной к кривой Г = f ( C ) в точке пересечения с осью ординат. Поверхностная активность может быть положительной и отрицательной. Значение и знак ее зависят от природы растворенного вещества и растворителя.

1. ₂ 0 : g >0 Þ с увеличением концентрации поверхностное натяжение на границе раздела фаз убывает и вещество поверхностно-активно .

1. ₂ / RT .