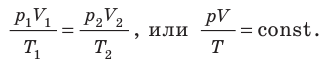Соотношение p = n k T – это формула, связывающая значение давления газа с его температурой и концентрацией молекул на единицу объема.
Они взаимодействуют со стенками сосуда посредствам упругих соударений. Данное выражение можно записать иначе, учитывая параметрические состояния объема V , давления p , температуры T и количества вещества ν . Применим неравенства:
n = N V = ν N А V = m M N A V .
Значением N является количество молекул данного сосуда, N А – постоянной Авогадро, m – массой газа в емкости, М – молярной массой газа. Исходя из этого, формула примет вид:
p V = ν N А k T = m M N А k T .
Произведение постоянной Авогадро N А на постоянную Больцмана k называют универсальной газовой постоянной и обозначают R .
По системе С И имеет значение R = 8 , 31 Д ж / м о л ь · К .
Соотношение p V = ν R T = m M R T получило название уравнения состояния идеального газа.
Один моль газа обозначается p V = R T .
При температуре T н = 273 , 15 К ( 0 ° C ) и давлении ρ н = 1 а т м = 1 , 013 · 10 5 П а говорят о нормальных условиях состояния газа.
Из уравнения видно, что один моль газа при нормальных условиях занимает один и тот же объем, равный v 0 = 0 , 0224 м 3 / м о л ь = 22 , 4 д м 3 / м о л ь . Выражение получило название закона Авогадро.
Если имеется смесь невзаимодействующих газов, то формулу запишем как:
p V = ν 1 + ν 2 + ν 3 + . . . R T ,
где ν 1 , v 2 , v 3 обозначает количество вещества каждого из них.
Еще в ХХ веке Б. Клапейрон получил уравнение, показывающее связь между давлением и температурой:
p V = ν R T = m M R T .
Впоследствии оно было записано Д.И. Менделеевым. Позже его назвали уравнением Клапейрона-Менделеева.
Задолго до получения уравнения состояния идеального газа на основе молекулярно-кинетической теории поведения газов изучались в различных условиях экспериментально. То есть уравнение p V = ν R T = m M R T служит обобщением всех опытных фактов.
Газ принимает участие в процессах с постоянно изменяющимися параметрами состояния: ( p , V и T ).
При протекании процессов медленно, система находится в состоянии, близком к равновесному. Процесс получил название квазистатического.
Соотнеся с происхождением процессов в нашем времени, то его протекания нельзя считать медленными.
Обычное время для разрежения и сжатия газа сотни раз в секунду. Это рассматривается как квазистатический процесс. Они изображаются с помощью диаграммы состояний параметров, где каждая из точек показывает равновесное состояние.
При неизменном одном параметре из ( p , V или T ) процесс принято называть изопроцессом.
- Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- График изотермического процесса. Основные термодинамические процессы
- Идеальные газы
- Главный закон
- Изотермический процесс
- Изменение внутренней энергии при изотермическом процессе
- Изобарный и изохорный процессы
- Изобарно-изотермический процесс
- 📹 Видео
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Видео:Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 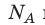
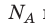
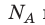
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
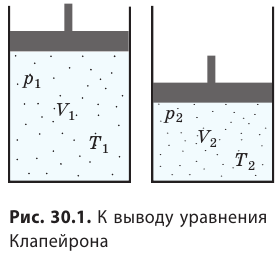
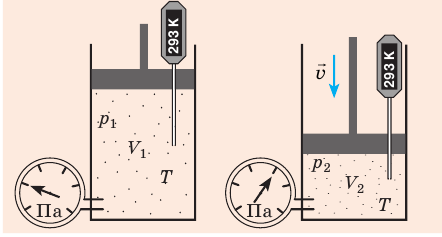
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (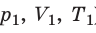
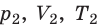
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 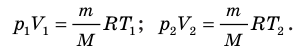
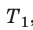
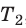
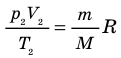
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
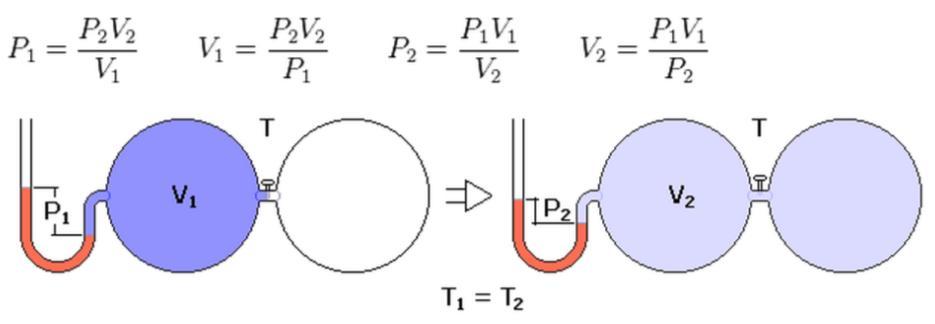
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (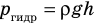
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (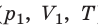
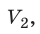
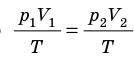
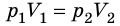
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 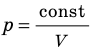
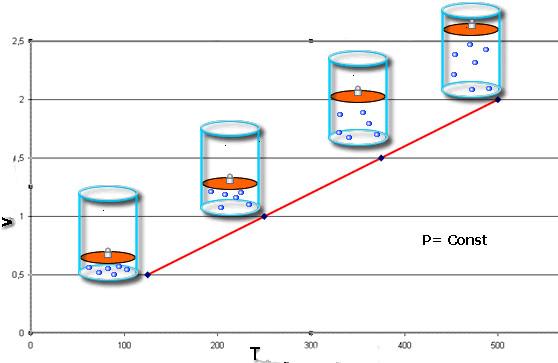
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (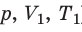
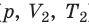
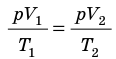
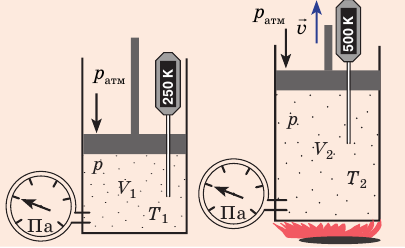
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (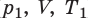
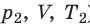
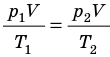
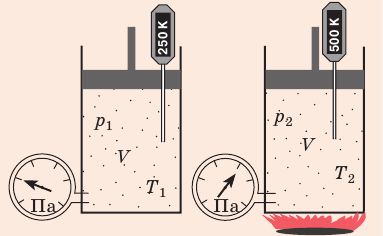
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 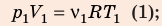
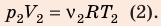

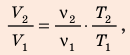
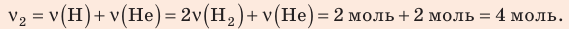
Ответ: примерно в 2,7 раза.
Пример №2
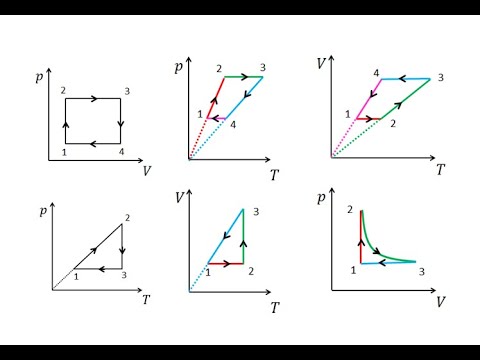
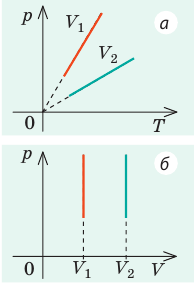
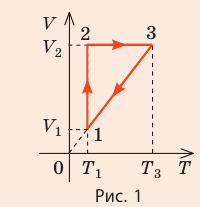
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
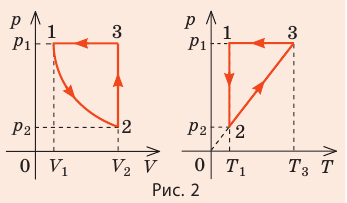
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Решение графических задач на тему Газовые законыСкачать

График изотермического процесса. Основные термодинамические процессы
Главным предметом изучения термодинамики газовых систем является изменение термодинамических состояний. В результате таких изменений газ может совершать работу и запасать внутреннюю энергию. Изучим в приведенной ниже статье разные термодинамические переходы в идеальном газе. Особое внимание будет уделено изучению графика изотермического процесса.
Видео:Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

Идеальные газы
Уже судя по самому названию, можно сказать, что 100-процентных идеальных газов в природе не существует. Однако многие реальные вещества удовлетворяют этой концепции с приемлемой для практики точностью.

Идеальным называется любой газ, в котором можно пренебречь взаимодействиями между его частицами и их размерами. Оба условия удовлетворяются только в том случае, если кинетическая энергия молекул будет намного превышать потенциальную энергию связей между ними, а расстояния между молекулами будут намного больше размеров частиц.
Чтобы определить, является ли изучаемый газ идеальным, можно воспользоваться простым эмпирическим правилом: если температура в системе выше комнатной, давление не сильно отличается от атмосферного или меньше него, а составляющие систему молекулы являются химически инертными, то газ будет идеальным.
Видео:Физика. МКТ: Графики газовых процессов. Центр онлайн-обучения «Фоксфорд»Скачать

Главный закон
Речь идет об уравнении идеального газа, которое также называется законом Клапейрона-Менделеева. Записано это уравнение было в 30-е годы XIX века французским инженером и физиком Эмилем Клапейроном. Спустя несколько десятилетий оно было приведено русским химиком Менделеевым к современному виду. Это уравнение имеет следующий вид:
В левой части равенства стоит произведение давления P на объем V, в правой части равенства — произведение температуры T на количество вещества n. Величина R — это универсальная газовая константа. Отметим, что T — это абсолютная температура, которая измеряется в кельвинах.
Закон Клапейрона-Менделеева впервые был получен из результатов предыдущих газовых законов, то есть в его основе лежала исключительно экспериментальная база. С развитием современной физики и кинетической теории текучих сред уравнение идеального газа может быть выведено из рассмотрения микроскопического поведения частиц системы.
Видео:Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Изотермический процесс
Независимо от того, происходит этот процесс в газах, в жидкостях или твердых телах, он имеет вполне четкое определение. Изотермическим называется такой переход между двумя состояниями, при котором температура системы сохраняется, то есть остается неизменной. Поэтому графиком изотермического процесса в осях времени (ось x) — температуры (ось y) будет горизонтальная линия.
Касательно газа идеального отметим, что изотермический переход для него называется законом Бойля-Мариотта. Обнаружен этот закон был экспериментальным путем. Причем он стал первым в этой области (вторая половина XVII века). Его может получить каждый школьник, если рассмотрит поведение газа в закрытой системе (n = const) при постоянной температуре (T = const). Пользуясь уравнением состояния, получаем:
Последнее равенство представляет собой закон Бойля-Мариотта. В учебниках по физике можно также встретить такую форму его записи:
При переходе из изотермического состояния 1 в термодинамическое 2 произведение объема на давление остается постоянным для закрытой газовой системы.
Изучаемый закон говорит об обратной пропорциональности между величинами P и V:
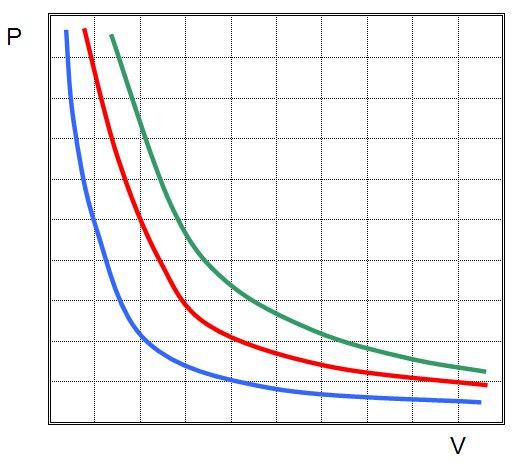
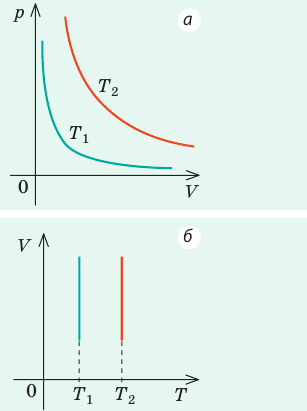
Это означает, что графиком изотермического процесса в идеальном газе будет кривая гипербола. Три гиперболы изображены на рисунке ниже.
Каждая из них называется изотермой. Чем выше температура в системе, тем дальше от осей координат будет стоять изотерма. Из рисунка выше можно сделать вывод, что зеленая соответствует самой высокой температуре в системе, а синяя — самой низкой при условии, что количество вещества во всех трех системах является одинаковым. Если же все изотермы на рисунке построены для одной температуры, то это означает, что зеленая кривая соответствует самой большой в плане количества вещества системе.
Видео:мкт ИЗОТЕРМИЧЕСКИЙ процесс ИЗОХОРНЫЙ процесс ИЗОБАРНЫЙ процессСкачать

Изменение внутренней энергии при изотермическом процессе
В физике идеальных газов под внутренней энергией понимают энергию кинетическую, связанную с вращательным и поступательным движением молекул. Из кинетической теории несложно получить следующую формулу для внутренней энергии U:
U = z / 2 * n * R * T.
Где z — это число степеней свободного движения молекул. Оно изменяется от 3 (одноатомный газ) до 6 (многоатомные молекулы).
В случае процесса изотермического температура остается постоянной, значит, единственной причиной изменения внутренней энергии является выход или приход в систему частиц вещества. Таким образом, в закрытых системах во время изотермического изменения их состояния внутренняя энергия сохраняется.
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Изобарный и изохорный процессы
Помимо закона Бойля-Мариотта, существуют еще два основных газовых закона, которые также были открыты экспериментальным путем. Они носят фамилии французов Шарля и Гей-Люссака. Математически их записывают так:
V / T = const при P = const;
P / T = const при V = const.
Закон Шарля говорит о том, что во время изобарного процесса (P = const) объем линейно зависит от абсолютной температуры. Закон Гей-Люссака свидетельствует о линейной зависимости между давлением и абсолютной температурой при изохорном переходе (V = const).
Из приведенных равенств следует, что от процесса изотермического графики изобарного и изохорного переходов отличаются существенным образом. Если изотерма имеет форму гиперболы, то изобара и изохора являются прямыми линиями.
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Изобарно-изотермический процесс
Рассматривая газовые законы, иногда забывают, что, помимо величин T, P и V, также может изменяться и величина n в законе Клапейрона-Менделеева. Если зафиксировать давление и температуру, то мы получим уравнение изобарно-изотермического перехода:
n / V = const при T = const, P = const.
Линейная зависимость между количеством вещества и объемом говорит о том, что при одинаковых условиях разные газы, содержащие одно и то же количество вещества, занимают равные объемы. Например, при нормальных условиях (0 oC, 1 атмосфера) молярный объем любого газа составляет 22,4 литра. Рассмотренный закон называется принципом Авогадро. Он лежит в основе закона Дальтона об идеальных газовых смесях.
📹 Видео
Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Изотермический процессСкачать

Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Физика. МКТ: Изотермический процесс. Центр онлайн-обучения «Фоксфорд»Скачать

Изопроцессы. Подготовка к ЕГЭ по Физике. Николай Ньютон. ТехноскулСкачать

Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Разбор задач на графики циклических процессовСкачать
Урок 147. Задачи на основное уравнение МКТ идеального газаСкачать

Применение первого начала термодинамики к изопроцессамСкачать

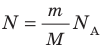
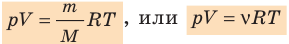
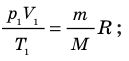
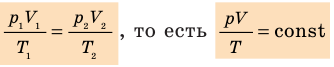
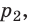
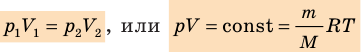

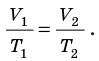
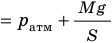
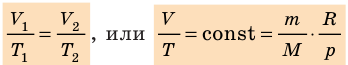
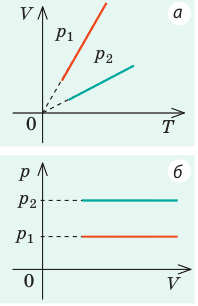

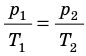
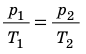
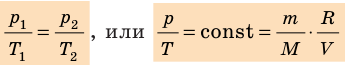

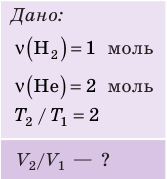
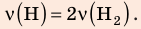

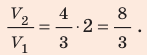
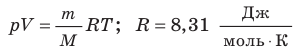 — универсальная газовая постоянная.
— универсальная газовая постоянная.