Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- Уравнение состояния идеального газа. Изопроцессы
- Уравнение изохорного процесса для данной массы идеального газа
- 📸 Видео
Видео:мкт ИЗОТЕРМИЧЕСКИЙ процесс ИЗОХОРНЫЙ процесс ИЗОБАРНЫЙ процессСкачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 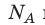
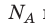
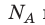
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
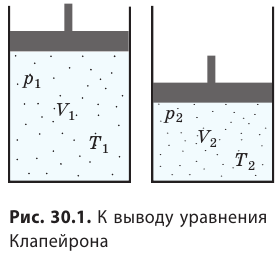
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (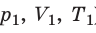
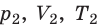
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 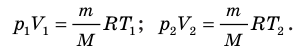
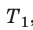
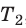
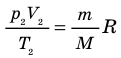
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (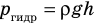
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (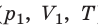
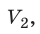
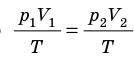
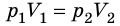
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 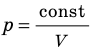
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (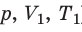
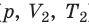
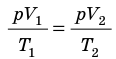
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
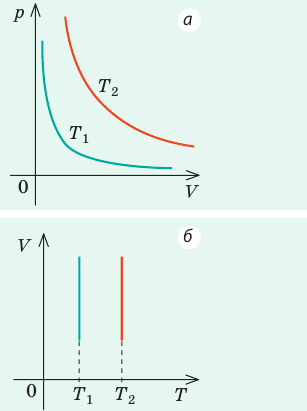
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (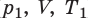
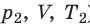
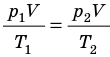
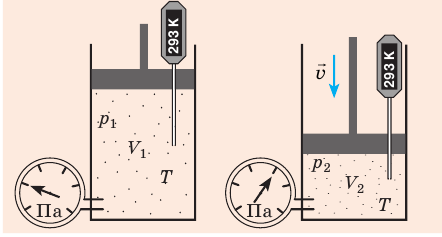
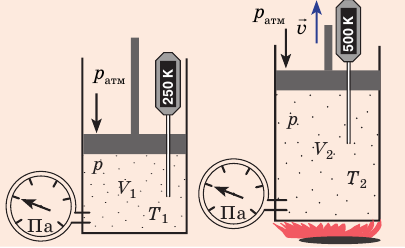
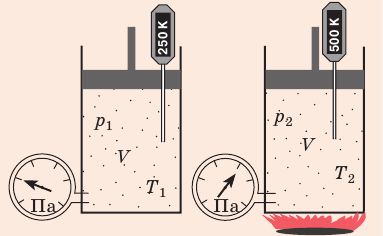
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
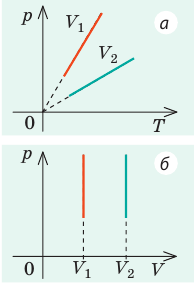
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 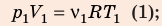
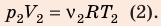

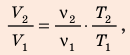
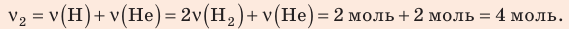
Ответ: примерно в 2,7 раза.
Пример №2
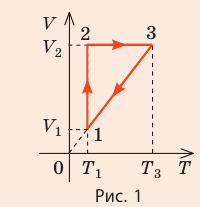
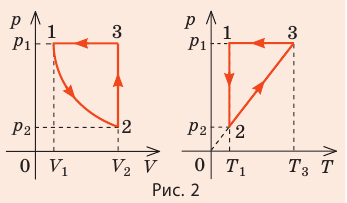
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Уравнение состояния идеального газа. Изопроцессы
Соотношение p = n k T – это формула, связывающая значение давления газа с его температурой и концентрацией молекул на единицу объема.
Они взаимодействуют со стенками сосуда посредствам упругих соударений. Данное выражение можно записать иначе, учитывая параметрические состояния объема V , давления p , температуры T и количества вещества ν . Применим неравенства:
n = N V = ν N А V = m M N A V .
Значением N является количество молекул данного сосуда, N А – постоянной Авогадро, m – массой газа в емкости, М – молярной массой газа. Исходя из этого, формула примет вид:
p V = ν N А k T = m M N А k T .
Произведение постоянной Авогадро N А на постоянную Больцмана k называют универсальной газовой постоянной и обозначают R .
По системе С И имеет значение R = 8 , 31 Д ж / м о л ь · К .
Соотношение p V = ν R T = m M R T получило название уравнения состояния идеального газа.
Один моль газа обозначается p V = R T .
При температуре T н = 273 , 15 К ( 0 ° C ) и давлении ρ н = 1 а т м = 1 , 013 · 10 5 П а говорят о нормальных условиях состояния газа.
Из уравнения видно, что один моль газа при нормальных условиях занимает один и тот же объем, равный v 0 = 0 , 0224 м 3 / м о л ь = 22 , 4 д м 3 / м о л ь . Выражение получило название закона Авогадро.
Если имеется смесь невзаимодействующих газов, то формулу запишем как:
p V = ν 1 + ν 2 + ν 3 + . . . R T ,
где ν 1 , v 2 , v 3 обозначает количество вещества каждого из них.
Еще в ХХ веке Б. Клапейрон получил уравнение, показывающее связь между давлением и температурой:
p V = ν R T = m M R T .
Впоследствии оно было записано Д.И. Менделеевым. Позже его назвали уравнением Клапейрона-Менделеева.
Задолго до получения уравнения состояния идеального газа на основе молекулярно-кинетической теории поведения газов изучались в различных условиях экспериментально. То есть уравнение p V = ν R T = m M R T служит обобщением всех опытных фактов.
Газ принимает участие в процессах с постоянно изменяющимися параметрами состояния: ( p , V и T ).
При протекании процессов медленно, система находится в состоянии, близком к равновесному. Процесс получил название квазистатического.
Соотнеся с происхождением процессов в нашем времени, то его протекания нельзя считать медленными.
Обычное время для разрежения и сжатия газа сотни раз в секунду. Это рассматривается как квазистатический процесс. Они изображаются с помощью диаграммы состояний параметров, где каждая из точек показывает равновесное состояние.
При неизменном одном параметре из ( p , V или T ) процесс принято называть изопроцессом.
Видео:Решение графических задач на тему Газовые законыСкачать

Уравнение изохорного процесса для данной массы идеального газа
| Законы идеальных газов |   |
| В XVII – XIX веках были сформулированы опытные законы идеальных газов. Кратко напомним их. Изопроцессы идеального газа – процессы, при которых один из параметров остаётся неизменным. 1. Изохорический процесс. Закон Шарля. V = const. Изохорическим процессом называется процесс, протекающий при постоянном объёме V. Поведение газа при этом изохорическом процессе подчиняется закону Шарля: При постоянном объёме и неизменных значениях массы газа и его молярной массы, отношение давления газа к его абсолютной температуре остаётся постоянным: P/Т = const. График изохорического процесса на РV-диаграмме называется изохорой. Полезно знать график изохорического процесса на РТ— и VT-диаграммах (рис. 1.6). Уравнение изохоры:
Изобарическим процессом называется процесс, протекающий при постоянном давлении Р. Поведение газа при изобарическом процессе подчиняется закону Гей-Люссака: При постоянном давлении и неизменных значениях массы и газа и его молярной массы, отношение объёма газа к его абсолютной температуре остаётся постоянным: V/T = const. График изобарического процесса на VT-диаграмме называется изобарой. Полезно знать графики изобарического процесса на РV— и РT-диаграммах (рис. 1.8).
Изотермическим процессом называется процесс, протекающий при постоянной температуре Т. Поведение идеального газа при изотермическом процессе подчиняется закону Бойля – Мариотта: При постоянной температуре и неизменных значениях массы газа и его молярной массы, произведение объёма газа на его давление остаётся постоянным: PV = const. График изотермического процесса на РV-диаграмме называется изотермой. Полезно знать графики изотермического процесса на VT— и РT-диаграммах (рис. 1.10).
Адиабатический процесс – термодинамический процесс, происходящий без теплообмена с окружающей средой. 5. Политропический процесс. Процесс, при котором теплоёмкость газа остаётся постоянной. Политропический процесс – общий случай всех перечисленных выше процессов. 6. Закон Авогадро. При одинаковых давлениях и одинаковых температурах, в равных объёмах различных идеальных газов содержится одинаковое число молекул. В одном моле различных веществ содержится NA=6,02·10 23 молекул (число Авогадро). 7. Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений Р, входящих в неё газов:
При
В соответствии с законами Бойля – Мариотта (1.4.5) и Гей-Люссака (1.4.3) можно сделать заключение, что для данной массы газа 📸 ВидеоУрок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать  Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать  Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать  Уравнение состояния идеального газа. 10 класс.Скачать  Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать  Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать  Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать  Изохорный процессСкачать  Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать  Физика. МКТ: Графики газовых процессов. Центр онлайн-обучения «Фоксфорд»Скачать  Урок 163. Задачи на графики процессов в газахСкачать  Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать  Физика 10 класс. Газовые законыСкачать  Физика. МКТ: Изохорный процесс. Центр онлайн-обучения «Фоксфорд»Скачать  Уравнение состояния идеального газаСкачать  Тема 6. Изотермический, изобарный и изохорный процессы изменения состояния идеального газаСкачать  |
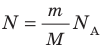
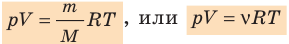
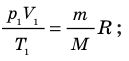
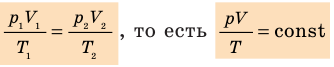
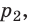
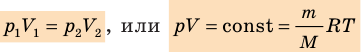

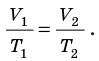
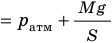
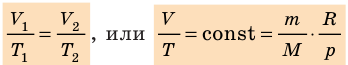
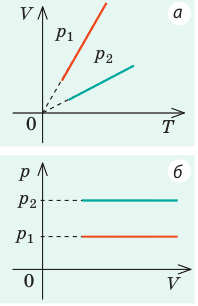

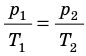
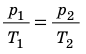
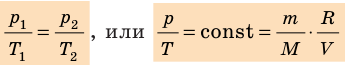

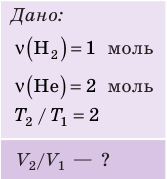
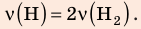

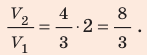
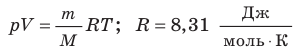 — универсальная газовая постоянная.
— универсальная газовая постоянная.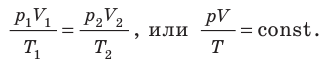




 .
.


 , давление смеси газов:
, давление смеси газов: