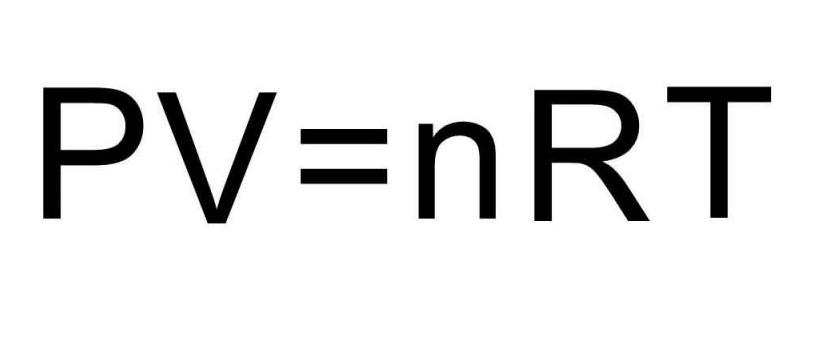Уравнение измерения внутренней энергии идеального газа

На этой странице вы можете рассчитать внутреннюю энергию идеального газа с помощью калькуляторов онлайн или самостоятельно по формулам.

Видео:Внутренняя энергия. 10 класс.Скачать

через массу, молярную массу и температуру

Формула для нахождения внутренней энергии идеального одноатомного газа через массу, молярную массу и температуру:

<U= dfrac cdot dfrac cdot R T> , где U — внутренняя энергия газа, m — масса газа, M — молярная масса газа, R — универсальная газовая постоянная R = 8,3144598(48) Дж⁄(моль∙К), T — абсолютная температура газа.

Видео:Физика 10 класс (Урок№23 - Внутренняя энергия. Работа. Количество теплоты.)Скачать

через давление и объем

Формула для нахождения внутренней энергии идеального одноатомного газа через давление и объем:

<U= dfrac cdot p V> , где U — внутренняя энергия газа, p — давление газа, V — объем газа.

Видео:Уравнение состояния идеального газа. 10 класс.Скачать

через количество вещества и температуру

Формула для нахождения внутренней энергии идеального одноатомного газа через количество вещества и температуру:

<U= dfrac cdot nu RT> , где U — внутренняя энергия газа, nu — количество вещества (в молях), R — универсальная газовая постоянная R = 8,3144598(48) Дж⁄(моль∙К), T — абсолютная температура газа.

Видео:Внутренняя энергия. Способы изменения внутренней энергии. 8 класс.Скачать

через степени свободы

Формула для нахождения внутренней энергии идеального одноатомного газа через количество вещества и температуру:

<U= dfrac cdot nu RT> , где U — внутренняя энергия газа, i — количество степеней свободы, nu — количество вещества (в молях), R — универсальная газовая постоянная R = 8,3144598(48) Дж⁄(моль∙К), T — абсолютная температура газа.

Количество степеней свободы молекулы идеального газа

Число степеней свободы (i) — наименьшее число независимых координат, которое необходимо ввести, чтобы определить положение тела в пространстве.

Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Внутренняя энергия и работа идеального газа

теория по физике 🧲 термодинамика

Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.

Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:

U = ∑ E k 0 = N E k 0 = m N A M . · i k T 2 . . = i 2 . . · m M . . R T = i 2 . . ν R T = i 2 . . p V

i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.

Видео:Физика. Термодинамика: Внутренняя энергия идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

Изменение внутренней энергии идеального газа в изопроцессах

Δ U = 3 2 . . · m M . . R T = 3 2 . . ν R T = 3 2 . . ν R ( T 2 − T 1 )

Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной.

Δ U = 3 2 . . ν R ( T 2 − T 1 ) = 3 2 . . ( p V 2 − p V 1 ) = 3 2 . . p Δ V

Δ U = 3 2 . . ν R ( T 2 − T 1 ) = 3 2 . . ( p 2 V − p 1 V ) = 3 2 . . V Δ p

Δ U = 3 2 . . ν R ( T 2 − T 1 ) = 3 2 . . ( p 2 V 2 − p 1 V 1 )

Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.

Видео:Урок 166. Предмет термодинамики. Внутренняя энергия телаСкачать

Работа идеального газа

Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:

Перемещение равно разности высот поршня в конечном и начальном положении:

Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:

Работа идеального газа

p — давление газа, S — площадь поршня

Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:

A ‘ = p ( V 2 − V 1 ) = p Δ V > 0

Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.

Работа идеального газа при изобарном сжатии:

A ‘ = p ( V 2 − V 1 ) = p Δ V 0

Работа идеального газа при нагревании газа:

A ‘ = ν R Δ T = ν R ( T 2 − T 1 ) = m M . . ν R Δ T

Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.

Видео:10 класс урок №44 Внутренняя энергия идеального газаСкачать

Геометрический смысл работы в термодинамике

В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).

Примеры графических задач

Изохорное охлаждение и изобарное сжатие:

Изобарное расширение: A ‘ = p ( V 2 − V 1 )
Изобарное сжатие: A ‘ = p ( V 2 − V 1 )
Изохорное охлаждение:
Замкнутый цикл: 1–2: A ‘ = ( p 1 − p 3 ) ( V 2 − V 1 )
Произвольный процесс: A ‘ = p 1 + p 2 2 . . ( V 2 − V 1 )

Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A₂ к A₁ в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:

A 2 = p ( V 2 − V 1 ) = 4 p ( 5 V − 3 V ) = 4 p 2 V = 8 p V

A 1 = p ( V 2 − V 1 ) = p ( 5 V − V ) = 4 p V

Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.

Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?

Для каждой величины подберите соответствующий характер изменения:

3) не изменяется

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения

1. Определить по графику, как меняется давление.
2. Определить, как меняется объем.
3. Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.

Решение

На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Один моль аргона, находящийся в цилиндре при температуре T₁=600 K и давлении p₁=4⋅10 5 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p₂=10 5 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?

Видео:Физика 10 класс Внутренняя энергия газа и ее изменениеСкачать

Формула внутренней энергии идеального газа. Изменение внутренней энергии газа: формула

Изучая поведение газов в физике, часто возникают задачи на определение запасенной в них энергии, которую теоретически можно использовать для совершения некоторой полезной работы. В данной статье рассмотрим вопрос, по каким формулам внутренняя энергия идеального газа может быть рассчитана.

Видео:Физика. 10 класс. Внутренняя энергия идеального газа. Термодинамическая работаСкачать

Понятие о газе идеальном

Четкое понимание концепции идеального газа важно при решении задач с системами, находящимися в этом агрегатном состоянии. Любой газ принимает форму и объем сосуда, в который его помещают, однако, не всякий газ является идеальным. Например, воздух можно считать смесью идеальных газов, в то же время водяной пар не является таковым. В чем же заключается принципиальная разница между реальными газами и их идеальной моделью?

Вам будет интересно: «Заклание» – это про необходимую жертву

Ответом на поставленный вопрос будут две следующие особенности:

• соотношение между кинетической и потенциальной энергией молекул и атомов, составляющих газ;
• соотношение между линейными размерами частиц газа и средним расстоянием между ними.

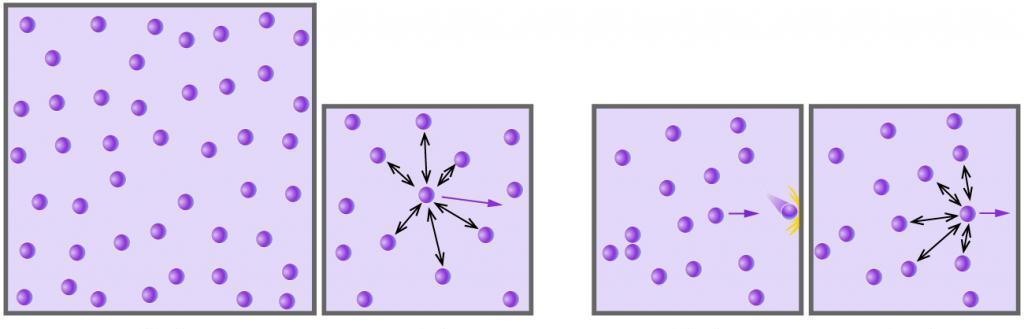
Газ считается идеальным только в том случае, когда средняя кинетическая энергия его частиц несоизмеримо больше энергии связи между ними. Разница между этими энергиями такова, что можно считать, что взаимодействие между частицами полностью отсутствует. Также для идеального газа характерно отсутствие размеров у его частиц, вернее эти размеры можно не учитывать, поскольку они намного меньше средних межчастичных расстояний.

Вам будет интересно: Московская лингвистическая школа: общая характеристика, основатель, представители

Хорошими эмпирическими критериями, позволяющими определить идеальность газовой системы, являются такие ее термодинамические характеристики, как температура и давление. Если первая больше 300 К, и второе меньше 1 атмосферы, то любой газ может полагаться идеальным.

Видео:Работа, совершаемая при термодинамических процессах. 10 класс.Скачать

Что это внутренняя энергия газа?

Прежде чем записать формулу внутренней энергии газа идеального, необходимо познакомится с этой характеристикой ближе.

В термодинамике внутреннюю энергию, как правило, обозначают латинской буквой U. Определяется в общем случае она по следующей формуле:

Где H — энтальпия системы, P и V — давление и объем.

По своему физическому смыслу внутренняя энергия состоит из двух составляющих: кинетической и потенциальной. Первая связана с различного рода движением частиц системы, а вторая — с силовым взаимодействием между ними. Если применить это определение к концепции газа идеального, у которого отсутствует потенциальная энергия, то величина U при любом состоянии системы будет точно равна его кинетической энергии, то есть:

Видео:Внутренняя энергия идеального газа | ФизикаСкачать

Вывод формулы внутренней энергии

Выше мы установили, что для ее определения у системы с идеальным газом необходимо рассчитать его кинетическую энергию. Из курса общей физики известно, что энергия частицы массой m, которая поступательно движется в некотором направлении со скоростью v, определяется по формуле:

Ее также можно применить для газовых частиц (атомов и молекул), однако, необходимо сделать некоторые замечания.

Во-первых, под скоростью v следует понимать некоторую среднюю величину. Дело в том, что газовые частицы движутся с разными скоростями согласно распределению Максвелла-Больцмана. Последнее позволяет определить среднюю скорость, которая с течением времени не изменяется, если отсутствуют внешние воздействия на систему.

Во-вторых, формула для Ek1 предполагает энергию на одну степень свободы. Газовые частицы могут двигаться во всех трех направлениях, а также вращаться в зависимости от их строения. Чтобы учесть величину степени свободы z, следует ее умножить на Ek1, то есть:

Кинетическая энергия всей системы Ek в N раз больше, чем Ek1z, где N — общее число газовых частиц. Тогда для U получаем:

Согласно этой формуле, изменение внутренней энергии газа возможно только в том случае, если поменять число частиц N в системе, либо их среднюю скорость v.

Видео:Внутренняя энергия | Физика 10 класс #38 | ИнфоурокСкачать

Внутренняя энергия и температура

Применяя положения молекулярно-кинетической теории идеального газа, можно получить следующую формулу связи между средней кинетической энергией одной частицы и абсолютной температурой:

Здесь kB — постоянная Больцмана. Подставляя это равенство в формулу для U, полученную в пункте выше, приходим к следующему выражению:

Данное выражение можно переписать через количество вещества n и газовую постоянную R в следующем виде:

В соответствии с этой формулой, изменение внутренней энергии газа возможно, если поменять его температуру. Величины U и T зависят друг от друга линейно, то есть график функции U(T) представляет собой прямую линию.

Видео:Физика Внутренняя энергия идеального газаСкачать

Как строение газовой частицы влияет на внутреннюю энергию системы?

Под строением частицы газа (молекулы) имеется в виду количество атомов, которое ее составляет. Оно играет определяющую роль при подстановке соответствующей степени свободы z в формулу для U. Если газ является одноатомным, формула внутренней энергии газа принимает такой вид:

Откуда взялась величина z=3? Ее появление связано всего с тремя степенями свободы, которыми обладает атом, поскольку он может двигаться только в одном из трех пространственных направлений.

Если рассматривается двухатомная молекула газа, то внутреннюю энергию следует вычислять по такой формуле:

Как видим, двухатомная молекула уже имеет 5 степеней свободы, 3 из которых являются поступательными и 2 вращательными (в соответствии с геометрией молекулы, она может вращаться вокруг двух взаимно перпендикулярных осей).

Наконец, если газ является трех- и более атомным, то справедливо следующее выражение для U:

Сложные молекулы имеют 3 поступательных и 3 вращательных степени свободы.

Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Пример задачи

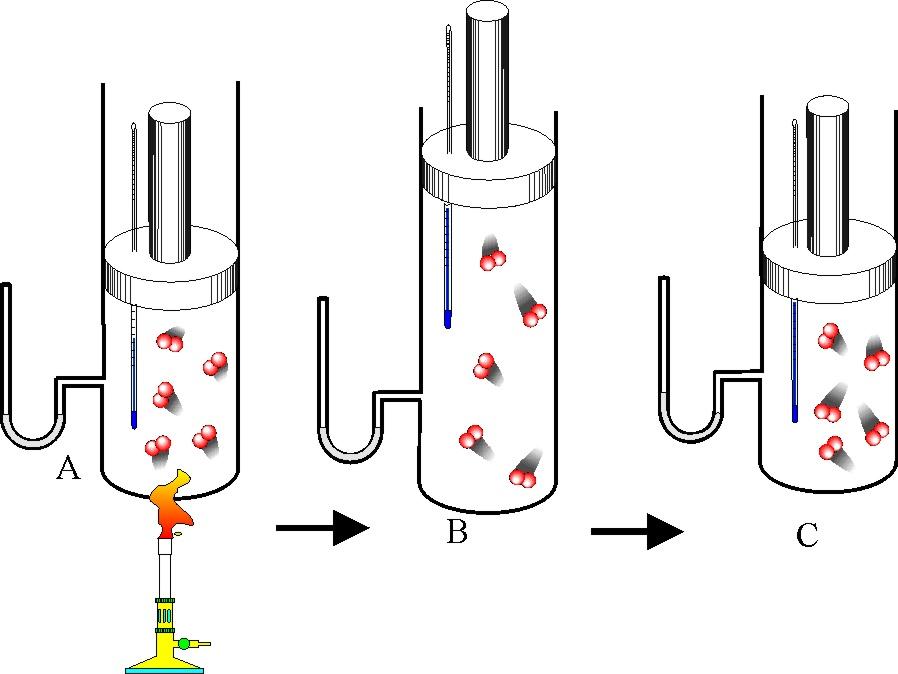
Под поршнем находится одноатомный газ при давлении 1 атмосфера. В результате нагрева газ расширился так, что его объем увеличился от 2-х литров до 3-х. Как при этом изменилась внутренняя энергия газовой системы, если процесс расширения был изобарным.

Чтобы решить эту задачу, недостаточно приведенных в статье формул. Необходимо вспомнить об уравнении состояния идеального газа. Оно имеет вид, представленный ниже.

Поскольку поршень закрывает цилиндр с газом, то в процессе расширения количество вещества n остается постоянным. Во время изобарного процесса температура изменяется прямо пропорционально объему системы (закон Шарля). Это означает, что формула выше запишется так:

Тогда выражение для внутренней энергии одноатомного газа примет форму:

Подставляя в это равенство значения давления и изменения объема в единицах СИ, получаем ответ: ΔU ≈ 152 Дж.

📽️ Видео

Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Внутренняя энергия. Практическая часть. 10 класс.Скачать

мкт РАБОТА В ТЕРМОДИНАМИКЕ внутренняя энергия идеального газаСкачать