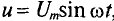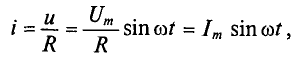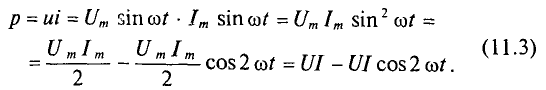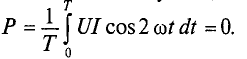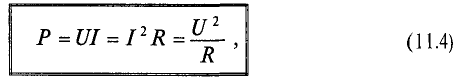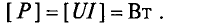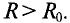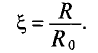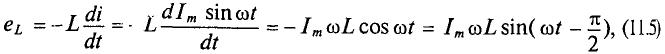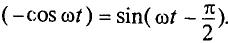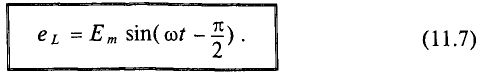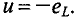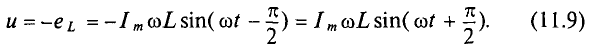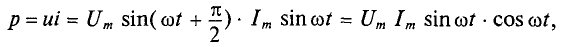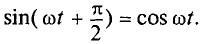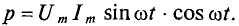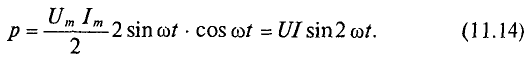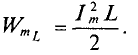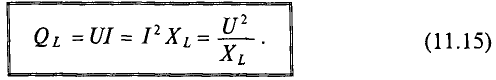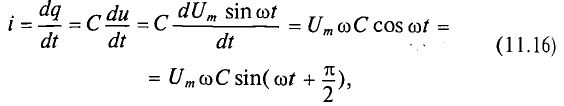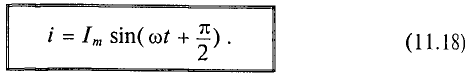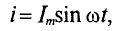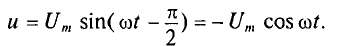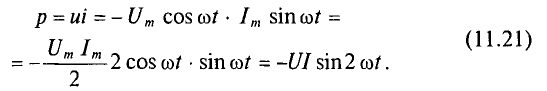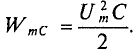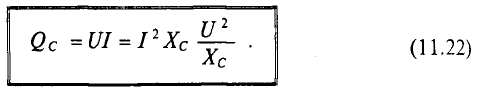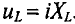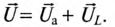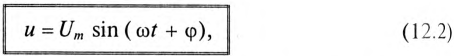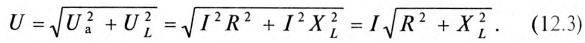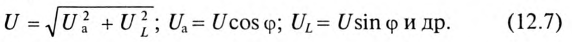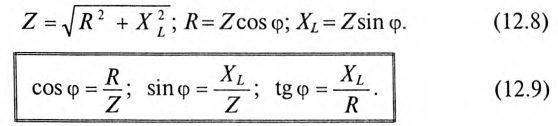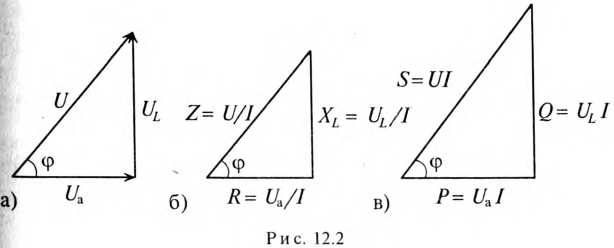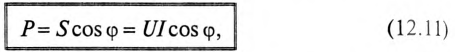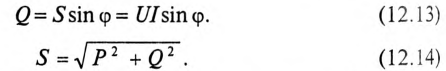Уравнение изменения мгновенного значения напряжения и силы тока на активном сопротивлении

«Физика — 11 класс»

Активное сопротивление

Сила тока в цепи с резистором

Есть цепь, состоящая из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R.

Сопротивление R называется активным сопротивлением, т.к. при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора.
Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Напряжение на зажимах цепи меняется по гармоническому закону:

u = U_m cos ωt

Мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения.
По закону Ома мгновенное значение силы тока:

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения, а амплитуда силы тока определяется равенством

Мощность в цепи с резистором

В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение меняются.
При прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет меняться во времени.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой

Р = I 2 R

Мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой

Р = i 2 R

Cреднее значение мощности за период (используем формулу для мгновенного значения силы тока и выражение ):

График зависимости мгновенной мощности от времени (рис.а):

Согласно графику (рис.б) среднее за период значение cos 2ωt равно нулю, а значит равно нулю второе слагаемое в формуле для среднего значения мощности за период.

Тогда средняя мощность равна:

Действующие значения силы тока и напряжения.

Среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока.
Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично:

Закон Ома для участка цепи переменного тока с резистором в действующих значениях:

В случае электрических колебаний важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность.
Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Действующие значения непосредственно определяют среднее значение мощности Р переменного тока:

р = I 2 R = UI.

Итак:
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика

Видео:Амплитуда, размах, действующее значение. Виды значений переменного тока. Ликбез.Скачать

Что такое активное сопротивление в цепи переменного тока

Переменный ток — основной источник бытового и промышленного электроснабжения. При подаче напряжения на потребителях возникает сопротивление. Статья даст подробное разъяснение, что такое активное сопротивление в цепи переменного тока.

Дополнительно будет дана формула расчета этого значения, описаны разновидности, условия для идеальной цепи и основные факторы, влияющие на увеличение этих значений.

Видео:Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

Переменный ток

Для того чтобы понять, что такое активное сопротивление, необходимо разобраться в самом явлении переменного тока. Переменным является такой тип тока, который непрерывно изменяет направление своего протекания. Во время протекания потенциалы переменного тока постоянно изменяются. Это происходит благодаря работе генератора, а точнее за счет взаимодействия магнитного поля с медной обмоткой. Движение хорошо прослеживается при помощи осциллографа. Своей формой оно напоминает синусоиду.

Роль переменного тока сложно переоценить. Главное его достоинство заключается в простоте передачи от источника к потребителю, возможность занижать или увеличивать напряжение при помощи трансформаторов. Также, переменные электрические токи можно доставлять потребителю с гораздо меньшими затратами.

Видео:Активное и реактивное сопротивление в цепи переменного тока. 11 класс.Скачать

Сопротивление

Сопротивлением является способность проводника замедлять прохождение заряженных частиц через свою структуру. На эту способность влияет материал проводника, его толщина и длина. Единицей измерения электрического сопротивления является 1 Ом.

Расчет производится при пропускании через проводник напряжения в один вольт и силой тока равной одному амперу. В электрических схемах данный параметр обозначается буквой «R».

Видео:Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Активное сопротивление

Переменный ток доставляется потребителю с целью его преобразования в иные виды энергии, например, тепло и свет. В бытовых сетях преобладает использование однофазного переменного тока. При подключении потребителя создается активное сопротивление.

Простые цепи переменного тока с активным сопротивлением включает в себя генератор тока и идеальный резистор. При этом должны соблюдаться необходимые условия для идеальной цепи:

1. Активное сопротивление не должно равняться нулю, обязательное условие.
2. Емкость и индуктивность цепи должны быть равны нулю.

Также, для идеального активного сопротивления должны соблюдаться следующие условия:

1. Соблюдаются закон Ома для мгновенных, среднеквадратичных и амплитудных параметров цепи.
2. Значение полностью независимо от амплитудных колебаний.
3. Между током и напряжением отсутствует сдвиг фаз.
4. Элемент, находящийся под напряжением, выделяет долю тепловой энергии, то есть нагревается.

Все эти условия позволяют электрическим приборам работать в пределах точно установленных параметров с максимальным КПД. Любое изменение может быть причиной отсутствия надежного контактного соединения или неисправностью самого потребителя.

Для того чтобы рассчитать величину активного сопротивления в цепи, необходимо знать величину напряжения и силы тока. Для расчета используется формула: R=U/I. Формула состоит из следующих значений:

1. «R» — сопротивление, Ом;
2. «U» — величина напряжения, вольт;
3. «I» — величина силы тока, ампер.

Далее можно сделать простой расчет. В качестве потребителя выступает электрическая печь, включенная в цепь однофазного переменного тока:

1. Напряжение цепи 240 вольт.
2. При замере силы тока получено значение 4 ампера.
3. R= 240/4=60 Ом.

Расчетная величина активного сопротивления — это не окончательное значение. На нее влияет прежде всего сечение проводов включенных в цепь, схема взаимодействия между цепями емкостных и полупроводниковых элементов.

Активное значение цепи также вызывает безвозвратную потерю первоначальной электрической энергии, а так же приводит к снижению мощности.

Видео:Урок 25. Что такое Переменный ТОК | Практические примерыСкачать

Активная емкость

В простой схеме величина активного значения также зависит от активной емкости. Для идеальной емкости — в схеме под переменным напряжением должен находится конденсатор. Идеальный конденсатор обозначается буквой «С».

Для получения идеальной цепи с активной емкостью, должны соблюдаться следующие условия:

1. Активная индуктивность и сопротивление должны быть равны 0.
2. Емкость самого конденсатора в цепи должна быть больше 0.

При данных условиях электрическая цепь приобретает следующие особенности:

1. Закон Ома соблюдается без малейших отклонений.
2. На переменный ток оказывается емкостное сопротивление «X».
3. Прослеживается нелинейное уменьшение емкости при повышении частоты колебаний.
4. Между напряжением и током происходит сдвиг по фазе до величины 90 градусов.
5. Емкость цепи непостоянна. Причина кроется в периодическом накоплении и отдаче энергии.

Цепь переменного тока с активным емкостным сопротивлением может дополняться индуктивностью. Для создания индуктивности, в цепь включается катушка индуктивности. Катушка также добавляет свою долю сопротивления в общую цепь. При таком подключении в схеме появляется индуктивное сопротивление. Оба элемента: катушка и конденсатор, не являются конечными потребителями энергии. Эти элементы не находятся под постоянным напряжением, их работа строится на накоплении и отдаче тока в цепь.

Видео:Переменный ток, действующее значение силы тока и напряженияСкачать

Мощность

При наличии активного сопротивления, значительно снижается мощность этой цепи. Это значение зависит от скорости снижения напряжения и преобразования электрической энергии. В электрической схеме мощность обозначается буквой «P».

Для того чтобы добиться минимального снижения средней и мгновенной мощностей, которые образуются в момент появления активного сопротивления, снижения напряжения и преобразования энергий, необходимо чтобы простейшие цепи состояли из идеальных элементов с высокой электрической проводимостью.

Видео:Амплитуда, период, частота и мгновенное значение переменного токаСкачать

Зависимость

Величина активного сопротивления во многом зависит от диаметра проводников. При подаче высокочастотных токов, сопротивление проводника может быть снижено, только если его поверхностный слой намного тоньше основного. Для того чтобы добиться идеального сечения, этот слой должен состоять из материала с очень высокой проводимостью, например, золота или серебра. Данный эффект возникает по причине взаимодействия напряжения и магнитного поля, образованного им. Поле сильно влияет на ток, протекающий по проводнику и выталкивает его на поверхностный слой. Таким образом ближе к поверхности проводника проводимость снижается и становится критично малой в его верхнем слое.

Так же присутствуют следующие эффекты: потери утечки и диэлектрические потери. Оба эффекта связаны с наличием конденсатора в цепи. Диэлектрические потери возникают за счет увеличения температуры диэлектрика внутри конденсатора. Потеря утечки возникает в следствии доли пробоя изолятор конденсатора.

Гистерезис. Это тоже тип потери энергии переменного тока. Такая потеря возникает при формировании магнитного поля вокруг предметов из металла. Электромагнитное воздействие приводит к нагреванию металла, а значит преобразованию энергии.

Последним фактором утечки является радиоизлучение. Радиоволны появляются по причине сильного магнитного поля и его взаимодействия с металлами цепи. Для подавления, особенно в радиоаппаратуре, используются экраны, которые впитывают часть поля и отталкивают остальную долю.

Видео:лекция 407 действующее значение напряженияСкачать

Замер

Измерение сопротивления осуществляется следующими способами:

1. Вольтметр и амперметр. С помощью этих приборов измеряются величины силы тока и напряжения, а после производится расчет по описанной выше формуле.
2. Логометром. Это прибор для измерения сопротивления под высоким напряжением и большой частотой. Его главное преимущество в сильном исключении зависимостей и погрешностей.
3. Омметр. Прибор используется только для измерения по типу усилителя сигнала. При использовании омметра учитывается высокая погрешность, которая может достигать 5 %. Обычные омметры электронного типа не подходят для замера активного сопротивления.

Видео:Переменный ток .Действующие значения силы тока и напряженияСкачать

Заключение

Активное сопротивление переменного тока важная величина. Она позволяет точно рассчитать, какая электроэнергия расходуется и какие ее утечки при этом возможны. В промышленных сетях при помощи этой величины рассчитывается доля потребления на различных участках с разными по мощности потребителями.

Видео:Активное сопротивление в цепи переменного токаСкачать

Видео по теме

Видео:Физика 11 класс (Урок№8 - Переменный электрический ток.)Скачать

Электрические цепи синусоидального тока

Содержание:

Видео:11 класс урок №15 Активное сопротивление в цепи переменного токаСкачать

Электрические цепи синусоидального тока:

В общем случае цепь переменного тока характеризуется тремя параметрами: активным сопротивлением R, индуктивностью L и емкостью С. В технике часто применяются цепи переменного тока, в которых преобладает один или два из этих параметров.

При анализе работы и расчетах цепей исходят из того, что для мгновенных значений переменного тока можно использовать все правила и законы постоянного тока.

Видео:Переменный ток. Активное сопротивление | Физика 11 класс #12 | ИнфоурокСкачать

Цепь с активным сопротивлением

Активным сопротивлением R обладают элементы, которые нагреваются при прохождении через них тока (проводники, лампы накаливания, нагревательные приборы и т.д.).

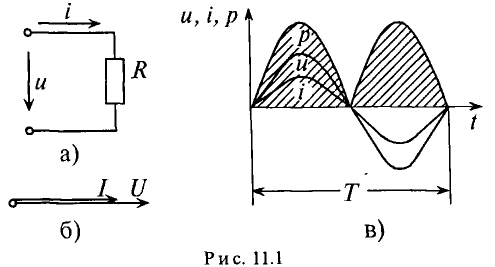
Если к активному сопротивлению R (рис. 11.1) приложено синусоидальное напряжение

где

Ток в цепи с активным сопротивлением совпадает по фазе с напряжением, так как начальные фазы их равны ( 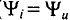= 0). Векторная диаграмма для цепи с активным сопротивлением изображена на рис. 11.16, временная диаграмма изображена на рис. 11.1в.

Математическое выражение закона Ома для цепи переменного тока с активным сопротивлением имеет вид:

Это вытекает из выражения (11.1), если левую и правую части уравнения разделить на 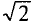=1,41.

Таким образом, действующее значение синусоидального тока I пропорционально действующему значению синусоидального напряжения U и обратно пропорционально сопротивлению R участка цепи, к которому приложено напряжение U. Такая интерпретация закона Ома справедлива как для мгновенных, так и для действующих и амплитудных значений синусоидального тока.

Активная мощность

Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения ка, т. е. р = ui. Это действие производится над кривыми тока и ряжения в определенном масштабе (рис. 11.1в). В результате учена временная диаграмма мгновенной мощности р. Как видно из временной диаграммы, мощность в цепи с активным сопротивлением изменяется по величине, но не изменяется по направлению (рис. 11.1в). Эта мощность (энергия) необратима. От источника она поступает на потребитель и полностью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется активной.

Поэтому и сопротивление R, на котором происходит подобное образование, называется активным сопротивлением, цепи с активным сопротивлением мгновенная мощность характеризует скорость преобразования электрической энергии в другие виды энергии.

Количественно мощность в цепи с активным сопротивлением определяется следующим образом:

Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин -постоянной мощности UI и переменной 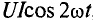, изменяющейся с двойной частотой.

Средняя за период мощность, равная постоянной составляющей мгновенной мощности UI, является активной мощностью Р. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть

Таким образом, величина активной мощности в цепи синусоидального тока с активным сопротивлением с учетом закона Ома определяется выражением:

где U- действующее значение напряжения; I— действующее значение тока.

Единицей активной мощности является ватт:

Поверхностный эффект и эффект близости

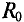
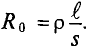
Сопротивление проводника постоянному току называют омическим сопротивлением и определяют выражением (2.8) Сопротивление проводника переменному току R называют активным.

Оказывается, что сопротивление проводника переменному току больше его омического сопротивления за счет так называемого поверхностного эффекта и эффекта близости, т. е.

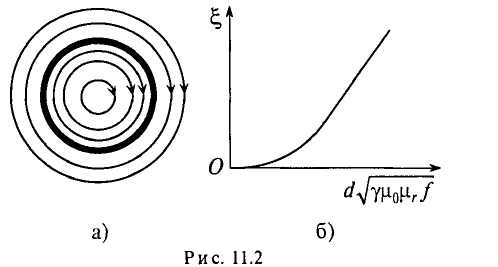
Увеличение активного сопротивления вызвано неодинаковой плотностью тока в различных сечениях проводника (рис. 11.2а).

На рис. 11.2а изображено магнитное поле проводника цилиндрического сечения. Если по проводнику проходит переменный ток, то он создает переменный магнитный поток внутри и вне проводника. Этот поток в различных сечениях проводника индуктирует ЭДС самоиндукции, которая, согласно правилу Ленца. противодействует изменению тока как причине создания ЭДС Очевидно, центр проводника охвачен большим количеством магнитных линий (большее потокосцепление), чем слои, близкие к поверхности. Следовательно, в центре проводника ЭДС (сопротивление) больше, чем на поверхности проводника. Плотность на поверхности больше, чем в центре. Поэтому это явление и называется поверхностным эффектом.

Таким образом, поверхностный эффект уменьшает сечение проводника для переменного тока, а следовательно, увеличивает активное сопротивление R.

Отношение активного сопротивления проводника к его сопротивлению определяет коэффициент поверхностного эффекта 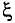(кси)

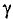
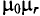
График зависимости коэффициента поверхностного эффекта от параметра проводника d, его удельной проводимости , магнитной проницаемости материала проводника и частоты переменного тока , проходящего по проводнику, показан на рис. 11.26.

При токах большой частоты (радиочастотах) ток в центре проводника отсутствует. Поэтому такие проводники делают трубчатыми, т.е. полыми.

На величину активного сопротивления проводника R оказывает влияние и эффект близости.

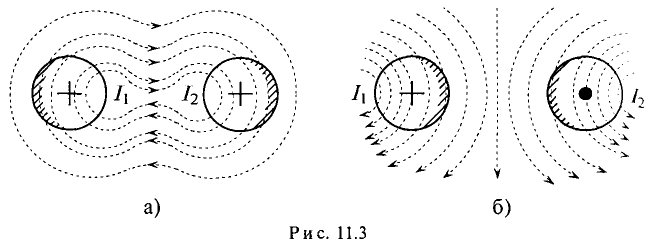
Если токи в двух параллельных проводах, расположенных близко друг к другу, направлены в одну сторону, то элементы сечения водников, удаленных на большее расстояние друг от друга, цепляются с меньшим магнитным потоком и имеют большую плотность тока (заштриховано на рис. 11.3а), чем элементы сечения проводников, расположенные близко друг к другу.

Если же токи в близко расположенных параллельных проводах направлены в различные стороны, то большая плотность тока на-дается в элементах сечения проводников, расположенных ближе друг к другу (заштриховано на рис. 11.36).

Таким образом, эффект близости в проводниках также влияет активное сопротивление проводников за счет наведения в различных элементах сечений проводников различных ЭДС взаимоиндукции, направление которых определяется правилом Ленца.

Видео:№45 ПР №12 "Вычисление мгновенного, максимального и действующего занач. ЭДС, напряжения, силы тока"Скачать

Цепь с идеальной индуктивностью

Идеальной называют индуктивность L такой катушки, активным сопротивлением R и емкостью С которой можно пренебречь, т.е. R= О и С=0.

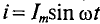
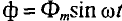
Если в цепи идеальной катушки индуктивностью L (рис. 11.4а) проходит синусоидальный ток , то этот ток создает в катушке синусоидальный магнитный поток , который индуктирует в катушке ЭДС самоиндукции, равную согласно (9.11)

так как

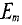
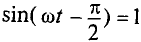
Очевидно, эта ЭДС достигает своего амплитудного значения тогда, когда :

Тогда

Таким образом, ЭДС самоиндукции в цепи с идеальной индуктивностью L, как и ток, вызвавший эту ЭДС, изменяется по синусоидальному закону, но отстает от тока по фазе на угол 90° = 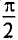(рис. 11.46, в).

По второму закону Кирхгофа для мгновенных значений можно записать

Откуда

Тогда напряжение, приложенное к цепи с идеальной индуктивностью (см. (11.5)):

Очевидно, напряжение достигает своего амплитудного значения U_m тогда, когда :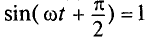

Следовательно,

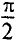
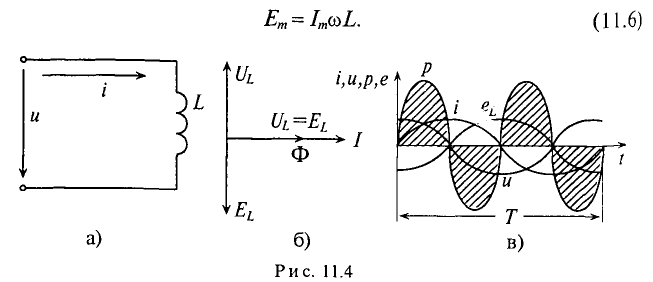
Таким образом, напряжение, приложенное к цепи с идеальной ин-ивностью, как и ток в этой цепи, изменяется по синусоидально-жону, но опережает ток по фазе на угол 90°= (рис. 11.46, в).

Резюмируя все вышесказанное, можно сделать вывод: для существования тока в цепи с идеальной индуктивностью необходимо ожить к цепи напряжение, которое в любой момент времени но по величине, но находится в противофазе с ЭДС, вызванной таким током (рис. 11.46, в).

Временная диаграмма (рис. 11.4в) еще раз иллюстрирует правило Ленца: ЭДС 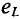противодействует изменению тока.

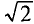
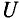
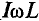
Если уравнение (11.10) разделить на =1,41, то получается =, откуда

Это уравнение (11.12а) и есть математическое выражение закона Ома для цепи синусоидального тока с идеальной индуктивностью. Очевидно, знаменатель этого уравнения есть не что иное, как сопротивление, которое называют индуктивным сопротивлением X_L.

Закон Ома для этой цепи можно записать иначе:

Индуктивное сопротивление X_L — это противодействие, которое ЭДС самоиндукции e_L оказывает изменению тока.

Реактивная мощность в цепи с индуктивностью

Мгновенная мощность для цепи синусоидального тока с идеальной катушкой равна произведению мгновенных значений напряжения и тока

где

Следовательно,

Полученное уравнение умножают и делят на 2:

Таким образом, мощность в цепи синусоидального тока с идеальной катушкой индуктивности изменяется по синусоидальному закону с двойной частотой.

Следовательно, среднее значение этой мощности за период Яс, как и любой синусоидальной величины, т. е. активная потребляемая мощность, в этой цепи равна нулю, Р= 0.

Временная диаграмма (рис. 11,4в) подтверждает этот вывод. На диаграмме видно, что мгновенная мощность (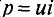) в рассматриваемой цепи изменяется по синусоидальному закону с двойной частотой.

То есть в 1-ю и 3-ю четверти периода мощность (энергия) источника накапливается в магнитном поле индуктивности. Максимальное значение накапливаемой в магнитном поле идеальной катушки энергии по (9.12) равно

Во 2-ю и 4-ю четверти периода эта мощность (энергия) из магнитного поля идеальной катушки возвращается к источнику.

Таким образом, в цепи переменного тока с идеальной катушки мощность не потребляется (Р= 0), а колеблется между источником и магнитным полем индуктивности, загружая источник и провода.

Такая колеблющаяся мощность (энергия), в отличие от активной, потребляемой, называется реактивной.

Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q]=вар (вольт-ампер реактивный).

Величина реактивной мощности в рассматриваемой цепи определяется выражением

Так как реактивная мощность Q_L имеет место в цепи с индуктивным сопротивлением, то индуктивное сопротивление считается реактивным сопротивлением X индуктивного характера, т. е. X_L.

Видео:Урок 359. Конденсатор и катушка индуктивности в цепи переменного тока.Скачать

Цепь с емкостью

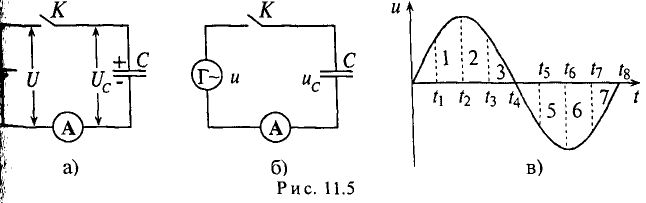
Если конденсатор емкостью С подключить к источнику с постоянным напряжением U (рис. 11.5а), то ток зарядки конденсатора ходит в цепи очень короткое время, пока напряжение на конденсаторе U_c не станет равным напряжению источника U.

Ток в рассматриваемой цепи (рис. 11.5а) практически отсутствует (амперметр А покажет I=0).

Если же конденсатор подключить к источнику с синусоидальным напряжением (рис. 11.56), то ток в цепи конденсатора существует все время, пока цепь замкнута, и амперметр А покажет этот ток. Ток в цепи конденсатора, подключенного к источнику с синусоидальным напряжением, имеет место потому, что напряжена конденсаторе U_c отстает по фазе от напряжения источника и зарядке, и при разрядке конденсатора. Например, пока напряжение на конденсаторе достигает значения 1, напряжение источника достигнет значения 2 (рис. 11.5в), т. е. конденсатор заряжается; пока конденсатор зарядится до напряжения 2, напряжение источника уменьшится до напряжения 3 — конденсатор разряжается на источник и т.д. Однако ток проходит только в цепи конденсатора. Через диэлектрик конденсатора ток не проходит.

Таким образом, если к конденсатору емкостью С приложено синусоидальное напряжение 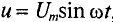, то в цепи конденсатора проходит ток i (рис. 11.6а):

где q= Си согласно (6.3).

Очевидно, ток в цепи конденсатора достигает амплитудного значения тогда, когда :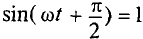

Тогда

Как видно, ток в цепи конденсатора, как и напряжение, приложенное к его обкладкам, изменяется по синусоидальному закону, однако опережает это напряжение по фазе на угол 90°=

Следовательно, напряжение отстает по фазе от тока на 90° = (рис. 11.66).

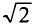
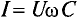
Если уравнение (11.17) разделить на = 1,41, то получится равенство или

Это равенство (11.19а) и является математическим выражением закона Ома для цепи переменного тока с емкостью.

Очевидно, знаменатель этого равенства является сопротивлением конденсатора Х_с, которое называется емкостным сопротивлением:

Когда закон Ома для цепи с конденсатором можно записать:

Емкостное сопротивление — это противодействие, которое оказывает напряжение заряженного конденсатора напряжению, приложенному к нему (рис. 11,5а).

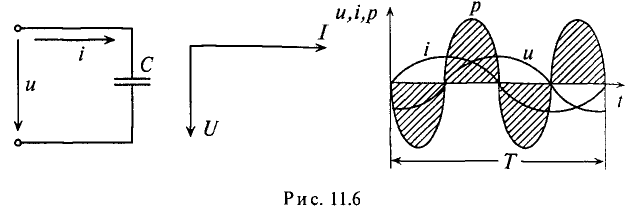
Реактивная мощность в цепи с конденсатором

Если в цепи конденсатора емкостью 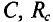= 0 (рис. 11.6а) проходит ток i, изменяющийся по синусоидальному закону:

Напряжение и, приложенное к этому конденсатору (рис. 11.6), будет равно

Мгновенная мощность в цепи с конденсатором

Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному закону с двойной частотой (рис. 11.6в).

Следовательно, активная мощность Р в рассматриваемой цепи 1С. 11.6а), равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р= 0.

Это следует и из временной диаграммы (рис. 11.6в). На временной диаграмме видно, что изменение мгновенной мощности р по синусоидальному закону происходит с двойной частотой: 2-ю и 4-ю четверти периода мощность (энергия) источника накапливается в электрическом поле конденсатора.

Максимальное значение энергии, накапливаемой в электрическом поле конденсатора, равно

В 1-ю и 3-ю четверти периода эта мощность (энергия) из электрического поля конденсатора возвращается к источнику.

Таким образом, в цепи переменного тока с конденсатором происходит колебание мощности (энергии) между источником и электрическим полем конденсатора. Такая колеблющаяся, но не потребляемая мощность называется реактивной мощностью.

Величина реактивной мощности в цепи конденсатора определяется выражением

Из временных диаграмм (рис. 11.4в, 11.6в) видно, что реактивная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении (11.21) — аналитическом выражении мгновенной мощности в цепи с конденсатором.

Так как реактивная мощность Qc имеет место в цепи с емкостным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением Х емкостного характера (Х_с).

Видео:Действующее значение переменного токаСкачать

Расчет линейных электрических цепей синусоидального тока

Расчет электрических цепей синусоидального тока производится преимущественно с помощью векторных диаграмм. В нашей главе рассматривается расчет неразветвленных цепей синусоидального тока, содержащих активное сопротивление R, активность L и емкость С в различных сочетаниях.

Цепь с активным сопротивлением и индуктивностью

Если по цепи с реальной катушкой, обладающей активным сопротивлением R и индуктивностью L, проходит синусоидальный ток 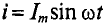(рис. 12.1а), то этот ток создает падение напряжения на активном сопротивлении проводников катушки и индуктивном сопротивлении катушки

Следовательно, по второму закону Кирхгофа, для мгновенных значений, приложенное к реальной катушке напряжение можно записать

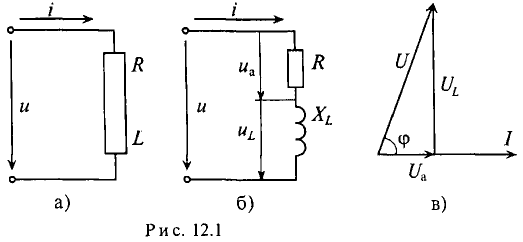
Это равенство справедливо для неразветвленной цепи синусоидального тока с последовательно включенными активным сопротивлением R и индуктивным сопротивлением X_L (рис. 12.16).

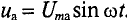
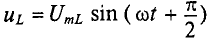
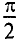
Активное напряжение (рис. 11.16) совпадет по фазе с током и может быть записано . Индуктивное напряжение опережает ток на угол 90° = .

Мгновенное значение напряжения, приложенного к цепи, определяется алгебраической суммой мгновенных значений напряжений 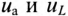согласно (12.1). А действующее значение этого напряжения U определяется геометрической суммой их действующих значений

Это равенство лежит в основе построения векторной диаграммы (рис. 12.1 в).

Из векторной диаграммы (рис. 12.1 в) видно, что напряжение U, приложенное к реальной катушке, опережает по фазе ток 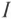на угол ф. Мгновенное значение этого напряжения может быть записано:

где ф — это международное обозначение угла сдвига фаз между током и напряжением для любой цепи переменного тока.

Воспользовавшись теоремой Пифагора для определения гипотенузы прямоугольного треугольника, по векторной диаграмме (рис. 12.1 в) определяется напряжение

Равенство (12.4) является математическим выражением закона Ома для цепи синусоидального тока с активным R и индуктивным XL сопротивлениями в неразветвленной цепи.

Знаменатель этого равенства является сопротивлением этой цепи, которое называется полным, или кажущимся, сопротивлением цепи синусоидального тока. Обозначается кажущееся (полное) сопротивление любой цепи переменного тока буквой Z:

где Z_k — полное, или кажущееся, сопротивление реальной катушки.

Тогда закон Ома для любой цепи переменного тока в общем виде можно записать

где Z — кажущееся сопротивление этой цепи.

Треугольники напряжений, сопротивлений, мощностей

Треугольник, все стороны которого изображены векторами напряжений, называется треугольником напряжений. Пользуясь векторной диаграммой для неразветвленной цепи с активным и индуктивным сопротивлениями (рис. 12.1в), выделяем треугольник напряжений (рис. 12.2а).

Связь между напряжениями в данной цепи можно рассматривать как соотношение между сторонами и углами прямоугольного треугольника:

Если все стороны треугольника напряжений разделить на ве-1ину тока в цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают сопротивления цепи, т. е. получится треугольник составлений (рис. 12.16). Сопротивления не являются векторными величинами. Из треугольника сопротивлений можно определить:

Обычно тригометрические функции угла ф определяются из треугольника сопротивлений отношением (12.9).

Если все стороны треугольника напряжений умножить на величину тока цепи, то получится подобный прямоугольный треугольник, все стороны которого в определенном масштабе изображают мощности цепи, т.е. получится треугольник мощностей (рис. 12.2в).

Произведение напряжения и тока цепи характеризует полную мощность цепи

которая измеряется в вольт-амперах, т.е.

Однако потребляется в цепи только часть полной мощности — активная мощность

где cos ф показывает, какая часть полной мощности 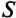потребляется в цепи, поэтому cos ф называют коэффициентом мощности:

Полная мощность цепи S называется кажущейся. Из того же треугольника мощностей (рис. 12.2в) записать:

Построив треугольники напряжений, сопротивлений и мощностей для любой цепи синусоидального тока, по выражениям (12.7)—(12.14) можно рассчитать параметры этой цепи.

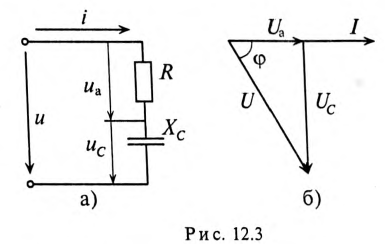
Цепь с активным сопротивлением и емкостью

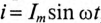
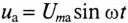
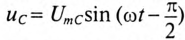
Если в цепи с последовательно включенными активным сопротивлением R и емкостью С протекает синусоидальный ток , то он создает падение напряжения на активном сопротивлении и на емкостном сопротивлении . Векторная диаграмма для этой цепи изображена на рис. 12.36.

Напряжение цепи изменяется, как и ток, по синусоидальному закону и отстает по фазе от тока на угол ф

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Видео:Активное и реактивное сопротивление в цепи переменного тока. Практ. часть -решение задачи. 11 класс.Скачать

Графики изменения напряжения и силы тока на активном сопротивлении

Скачать
презентациюПонятие действующего значения >>

Графики изменения напряжения и силы тока на активном сопротивлении. Колебания напряжения и силы тока на активном сопротивлении совпадают по фазе. Время, с. Колебания напряжения. Колебания силы тока. Активное сопротивление в цепи переменного тока.

Слайд 6 из презентации ««Переменный ток» физика» к урокам физики на тему «Переменный ток»

Размеры: 960 х 720 пикселей, формат: jpg. Чтобы бесплатно скачать слайд для использования на уроке физики, щёлкните на изображении правой кнопкой мышки и нажмите «Сохранить изображение как. ». Скачать всю презентацию ««Переменный ток» физика.ppt» можно в zip-архиве размером 446 КБ.

Видео:Физика. 11 класс. Активное и реактивное сопротивления в цепи переменного тока /24.09.2020/Скачать

Переменный ток

«Уравнения трансформаторов» — Уравнения трансформатора в режиме холостого хода. Магнитные системы микротрансформаторов. Виток обмотки. Конструкция силовых трансформаторов. Уравнения трансформатора. Схема двухобмоточного трансформатора. Принципы соединения обмоток. Конструкция трансформаторов. Группы соединений. Элементы обмотки.

«Трехфазные цепи» — Фазные и линейные напряжения. Значения фазных и линейных напряжений. Звезда. Активная мощность трехфазной цепи. Комплексные амплитуды ЭДС. Векторная диаграмма ЭДС. Cимметричная система ЭДС. Соединение обмоток генератора. Принцип получения источника многофазной ЭДС. Cимметричная многофазная система. Многофазный источник ЭДС.

«Цепи переменного тока» — ? – сдвиг фаз между колебаниями тока и напряжения Im – амплитуда тока, А. Размерность: Или. Хлеборезка. Действующее значение напряжения: В такой цепи: Действующие значения напряжения и силы тока. Ответы теста. Резистор в цепи переменного тока. Переменный электрический ток. Переменным током называется электрический ток, изменяющийся во времени по модулю и направлению.

«Схема электронного трансформатора» — Схема электронного трансформатора). На элементах R2, R3, C4, D5, D6 собрана цепь запуска автогенератора в момент включения всего устройства в сеть. Выпрямленное входным диодным мостом напряжение сети через резистор R2 заряжает конденсатор C4. Трансформатор. Электронный трансформатор. Управляющий трансформатор Т1 намотан на ферритовом кольце с внешним диаметром 8 мм.

«Синусоидальный ток» — Период переменного тока. Векторные диаграммы токов. Комплексное электрическое сопротивление. Уравнения для напряжений и ЭДС. Действующий синусоидальный ток. Аргумент. Комплексная проводимость. Представление синусоидального тока вращающимся вектором. Мнимая и вещественная части. Изображение синусоидального тока.

««Переменный ток» физика» — Сопротивление проводника. Колебания тока на конденсаторе. Индуктивность в цепи переменного тока. Что такое индуктивность. Графики тока и напряжения на конденсаторе. Проанализируем формулу индуктивного сопротивления. Сопротивление. Действующие значения тока и напряжения. Ток в катушке индуктивности. Активное сопротивление в цепи переменного тока.

Всего в теме «Переменный ток» 22 презентации

🎥 Видео

Урок 55. Переменный ток. Действующие значения I и U. Ёмкостное и индуктивное сопротивления.Скачать

В чём разница между НАПРЯЖЕНИЕМ и ТОКОМСкачать