Уравнение изменение заряда от времени (3 видео)

Уравнение изменение заряда от времени

Электромагнитные колебания и волны

Для колебательного контура предыдущей задачи написать уравнение (с числовыми коэффициентами) изменения со временем t энергии электрического поля W_эл, энергии магнитного поля W_м и полной энергии поля W. Найти энергию электрического поля, энергию магнитного поля и полную энергию поля в моменты времени Т/8, Т/4 и Т/2. Построить графики этих зависимостей в пределах одного периода.

Дано:

q = 2,5 мкКл = 2,5·10 -6 Кл

Решение:

Энергия электрического поля на обкладках конденсатора

Энергия магнитного поля в катушке индуктивности

Полная энергия в контуре

Закон изменения напряжения на обкладках конденсатора

Период колебаний находим по формуле Томсона

Циклическая частота связана с периодом соотношением

Уравнение колебания напряжения запишется в виде

Аналогично можно записать уравнение изменения заряда на обкладках конденсатора

Ток в контуре – первая производная от заряда по времени

Содержание

Зарядка конденсатора от источника постоянной ЭДС
Примечания
Решение задач по теме «Электромагнитные колебания и волны» на примере разбора задач ЕГЭ
Презентация к уроку
📺 Видео

Видео:Конденсаторы. Процессы заряда и разряда конденсатораСкачать

Зарядка конденсатора от источника постоянной ЭДС

Рассмотренный в предыдущем разделе процесс зарядки конденсатора посредством перенесения заряда с одной обкладки на другую имеет исключительно теор етический интерес, как метод расчета энерги и конденсатора. Реально конденсаторы заряжают, подключая их к источнику ЭДС, например, к гальванической батарее.

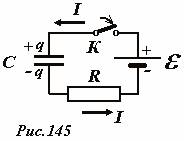
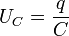
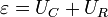
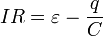
Пусть конденсатор емкостью C подключен к источнику, ЭДС которого равна e (Рис. 145). Полное электрическое сопротивление цепи (включающее и внутренне сопротивление источника) обо значим R . При замыкании ключа в цепи пойдет электрический ток, благодаря которому на обкладках конденсатора будет накапливаться электрический заряд. По закону Ома сумма напряжений на конденсаторе и резисторе U R = I R равна ЭДС источника , что приводит к уравнению

. (1)

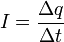
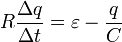
В этом уравнении заряд конденсатора и сила тока зависят от времени. Скорость изменения заряда конденсатора по определению равна силе тока в цепи , что позволяет получить уравнение, описывающее изменение заряда конденсатора с течением времени

. (2)

Можно также получить уравнение, непосредственно описывающее изменение силы тока в цепи с течением времени. Для этого на основании уравнения (1) запишем уравнения для малых изменений входящих величин

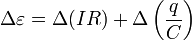
Формально эту операцию можно описать следующим образом: уравнение (1) следует записать для двух моментов времени t и ( t + Delta t ), а затем из второго уравнения вычесть первое. Так как ЭДС источника постоянна, то ее изменение равно нулю Delta e = 0, сопротивление цепи и емкость конденсатора постоянны, поэтому их можно вынести из под знака изменения Delta, поэтому полученное уравнение приобретает вид

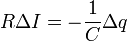
Наконец разделим его на промежуток времени, в течение которого произошли эти изменения, в результате получаем искомое уравнение (с учетом связи между силой тока и изменения заряда)

. (3)

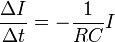
Математический смысл этого уравнения указывает, что скорость уменьшения тока пропорциональна самой силе тока. Для однозначного решения этого уравнения необходимо задать начальное условие – значение силы тока в начальный момент времени I 0 = I(0).

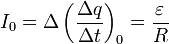
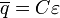
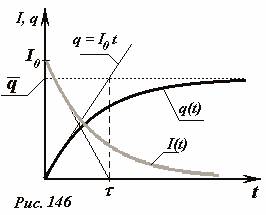
С уравнениями такого типа мы познакомились в «математическом отступлении» , поэтому здесь его анализ проведем кратко. В начальный момент времени, когда заряд конденсатора равен нулю, скорость возрастания заряда (то есть сила тока) максимальна и равна . Затем по мере накопления заряда сила тока будет уменьшаться, когда напряжение на конденсаторе станет равным ЭДС источника, заряд конденсатора достигнет максимального стационарного значения и ток в цепи прекратится.

Схематически зависимости заряда конденсатора и силы тока в цепи от времени показаны на рис. 146. Для оценки времени зарядки конденсатора можно принять, что заряд возрастает до максимального значения с постоянной скоростью, равной силе тока в начальный момент времени. В этом случае

. (4)

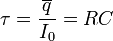
Аналогичная оценка исчезновения тока, полученная на основании уравнения (3) приводит к этому же результату.

Строго говоря, время зарядки конденсатора, описываемой уравнением (2) равно бесконечности. Это парадокс можно исключить, если принять во внимание дискретность электрического заряда. Кроме того, заряд конденсатора, подключенного к батарее с течением времени случайным образом изменяется, флуктуирует, поэтому рассматриваемое уравнение описывает некоторые усредненные характеристики процесса. Тем не менее, полученная оценка времени RC широко применяется в приближенных расчетах, часто ее называют просто временем зарядки конденсатора .

Рассмотрим теперь превращения различных форм энерги и в данном процессе. Понятно, что причиной тока в цепи и как следствие зарядки конденсатора являются сторонние силы источника. 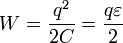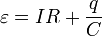На первый взгляд, энергетический баланс включает определенное противоречие: если источник сообщил конденсатору заряд q , то сторонние силы совершили при этом работу A 0 = q e , при этом энерги я конденсатора стала равной , что в два раза меньше работы совершенной источником. Противоречие исчезает, если принять во внимание, что в процессе зарядки по цепи течет электрический ток, поэтому на резисторе выделяется некоторое количество теплоты, то есть часть энерги и источника переходит в тепловую. Мысленно разобьем время зарядки на малые промежутки Delta t i ( i = 1,2,3. ). Перепишем уравнение (1) в виде

, (5)

и умножим его на величину малой порции заряда, переносимого за малый промежуток времени Delta t i , Delta q i = I i Delta t i . В результате получим

. (6)

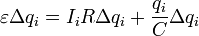
Здесь обозначено q i — заряд конденсатора перед перенесением рассматриваемой порции заряда. Каждый член полученного уравнения имеет явный физический смысл :

— работа сторонних сил по перемещению порции заряда ? q i ; — увеличение энерги и конденсатора при увеличении его заряда на Delta q i ; — количество теплоты, выделившееся на резисторе, при протекании

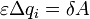
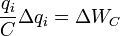
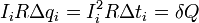
порции заряда Delta q i .

Таким образом, закон сохранения энерги и, выражаемый уравнением баланса (6) для малого промежутка времени оказывается выполненным, следовательно, он будет выполнен и для всего процесса зарядки. Просуммируем выражение (5) по всем промежуткам времени зарядки, в результате чего получим:

— полная работа сторонних сил по перенесению электрического заряда, равного стационарному заряду конденсатора; — энерги я заряженного конденсатора; наконец, — количество выделившейся на резисторе теплоты.

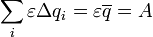
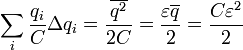
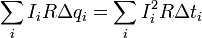
Принимая во внимание уравнение (3) и формулы из «математического отступления» , последнюю сумму можно выразить в виде

. (6)

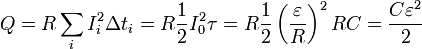
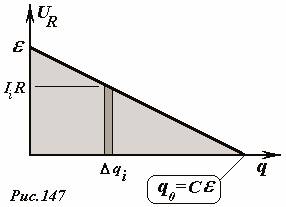
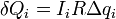
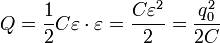
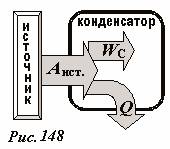
Эта сумма же может быть вычислена графически. Формула (1) задает зависимость напряжения на резисторе U R = I R от заряда конденсатора. Эта зависимость линейна, ее график (Рис. 147) является отрезком прямой линии. За малый промежуток времени через резистор протечет малый заряд Delta q i , при этом выделится количество теплоты , которое численно равно площади узкой полоски, выделенной на рисунке. Полное количество теплоты, выделившейся при прохождении всего заряда численно равно площади треугольника под графиком зависимости U R ( q ), то есть

. (7)

Таким образом, энергетический баланс полностью сходится и для всего процесса целиком: работа, совершенная источником равна сумме энерги и конденсатора и количества выделившейся теплоты A = W C + Q . Схематически преобразование энерги и в этом процессе показано на рис. 148.

Интересно заметить, что количество теплоты, выделяющееся при зарядке, не зависит о сопротивления цепи и в точности равно энерги и конденсатора. То есть, половина энерги и источника переходит в энерги ю электрического поля, а вторая в тепловую энерги ю, выделяющуюся в цепи: природа требует своеобразный пятидесятипроцентный налог в виде тепловых потерь, не зависимо от сопротивления цепи и емкости конденсатора [1] .

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Примечания

^ Но эти параметры цепи определяют время процесса.

Об авторе:
Этот материал взят из источника в свободном доступе интернета. Вся грамматика источника сохранена.

Видео:Графические зависимости заряда и силы тока от времени в идеальном колебательном контуре. 11 класс.Скачать

Решение задач по теме «Электромагнитные колебания и волны» на примере разбора задач ЕГЭ

Презентация к уроку

Цели урока:

Образовательные: обобщение и систематизация знаний по теме, проверка знаний, умений, навыков. В целях повышения интереса к теме работу вести с помощью опорных конспектов.
Воспитательные: воспитание мировоззренческого понятия (причинно-следственных связей в окружающем мире), развитие у школьников коммуникативной культуры.
Развивающие: развитие самостоятельности мышления и интеллекта, умение формулировать выводы по изученному материалу, развитие логического мышления, развитие грамотной устной речи, содержащей физическую терминологию.

Тип урока:систематизация и обобщение знаний.

Техническая поддержка урока:

Демонстрации:
Плакаты.
Показ слайдов с помощью информационно – компьютерных технологий.
Дидактический материал:
Опорные конспекты с подробными записями на столах.
Оформление доски:
Плакат с кратким содержанием опорных конспектов (ОК);
Плакат – рисунок с изображением колебательного контура;
Плакат – график зависимости колебаний заряда конденсатора, напряжения между обкладками конденсатора, силы тока в катушке от времени, электрической энергии конденсатора, магнитной энергии катушки от времени.

План урока:

1. Этап повторения пройденного материала. Проверка домашнего задания.
Четыре группы задач по теме:

Электромагнитные колебания.
Колебательный контур.
Свободные колебания. Свободные колебания – затухающие колебания
Характеристика колебаний.

2. Этап применения теории к решению задач.
3. Закрепление. Самостоятельная работа.
4. Подведение итогов.

Учитель: Темой урока является «Решение задач по теме: «Электромагнитные колебания и волны» на примере разбора задач ЕГЭ»

К доске вызываются 3 ученика для проверки домашнего задания.

– Задания по этой теме можно разделить на четыре группы.

Четыре группы задач по теме:

1. Задачи с использованием общих законов гармонических колебаний.
2. Задачи о свободных колебаниях конкретных колебательных систем.
3. Задачи о вынужденных колебаниях.
4. Задачи о волнах различной природы.

– Мы остановимся на решении задач 1 и 2 групп.

Урок начнем с повторения необходимых понятий для данной группы задач.

Электромагнитные колебания – это периодические и почти периодические изменения заряда, силы тока и напряжения.

Колебательный контур – цепь, состоящая из соединительных проводов, катушки индуктивности и конденсатора.

Свободные колебания – это колебания, происходящие в системе благодаря начальному запасу энергии с частотой, определяемой параметрами самой системы: L, C.

Скорость распространения электромагнитных колебаний равна скорости света: С = 3 . 10 8 (м/с)

Основные характеристики колебаний

Амплитуда (силы тока, заряда, напряжения) – максимальное значение (силы тока, заряда, напряжения): Im, Qm, Um
Мгновенные значения (силы тока, заряда, напряжения) – i, q, u

Схема колебательного контура

Учитель: Что представляют электромагнитные колебания в контуре?

Электромагнитные колебания представляют периодический переход электрической энергии конденсатора в магнитную энергию катушки и наоборот согласно закону сохранения энергии.

Задача №1 (д/з)

Колебательный контур содержит конденсатор емкостью 800 пФ и катушку индуктивности индуктивностью 2 мкГн. Каков период собственных колебаний контура?

Задача № 2 (д/з)

Колебательный контур состоит из конденсатора емкостью С и катушки индуктивности индуктивностью L. Как изменится период свободных электромагнитных колебаний в этом контуре, если электроемкость конденсатора и индуктивность катушки увеличить в 3р.

Задача № 3 (д/з)

Амплитуда силы тока при свободных колебаниях в колебательном контуре 100 мА. Какова амплитуда напряжения на конденсаторе колебательного контура, если емкость этого конденсатора 1 мкФ, а индуктивность катушки 1 Гн? Активным сопротивлением пренебречь.

Схема электромагнитных колебаний

Ученик 1 наглядно описывает процессы в колебательном контуре.

Ученик 2 комментирует электромагнитные колебания в контуре, используя графическую зависимость заряда, напряжения. Силы тока, электрической энергии конденсатора, магнитной энергии катушки индуктивности от времени.

Уравнения, описывающие колебательные процессы в контуре:

Обращаем внимание, что колебания силы тока в цепи опережают колебания напряжения между обкладками конденсатора на π/2.
Описывая изменения заряда, напряжения и силы тока по гармоническому закону, необходимо учитывать связь между функциями синуса и косинуса.

Задача № 1.

По графику зависимости силы тока от времени в колебательном контуре определите, какие преобразования энергии происходят в колебательном контуре в интервале времени от 1мкс до 2мкс?

1. Энергия магнитного поля катушки увеличивается до максимального значения;
2. Энергия магнитного поля катушки преобразуется в энергию электрического поля конденсатора;
3. Энергия электрического поля конденсатора уменьшается от максимального значения до «о»;
4. Энергия электрического поля конденсатора преобразуется в энергию магнитного поля катушки.

Задача № 2.

По графику зависимости силы тока от времени в колебательном контуре определите:

а) Сколько раз энергия катушки достигает максимального значения в течение первых 6 мкс после начала отсчета?
б) Сколько раз энергия конденсатора достигает максимального значения в течение первых 6 мкс после начала отсчета?
в) Определите по графику амплитудное значение силы тока, период, циклическую частоту, линейную частоту и напишите уравнение зависимости силы тока от времени.

Задача № 3 (д/з)

Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите, какое преобразование энергии происходит в интервале времени от 0 до 2 мкс?

Задача № 4 (д/з)

Дана графическая зависимость напряжения между обкладками конденсатора от времени. По графику определите: сколько раз энергия конденсатора достигает максимального значения в период от нуля до 2мкс? Сколько раз энергия катушки достигает наибольшего значения от нуля до 2 мкс? По графику определите амплитуду колебаний напряжений, период колебаний, циклическую частоту, линейную частоту. Напишите уравнение зависимости напряжения от времени.

К доске вызываются 2 ученика

Задача № 5, 6

Задача № 7

Заряд на обкладках конденсатора колебательного контура изменяется по закону
q = 3·10 –7 cos800πt. Индуктивность контура 2Гн. Пренебрегая активным сопротивлением, найдите электроемкость конденсатора и максимальное значение энергии электрического поля конденсатора и магнитного поля катушки индуктивности.

Задача № 8

В идеальном колебательном контуре происходят свободные электромагнитные колебания. В таблице показано, как изменяется заряд конденсатора в колебательном контуре с течением времени.

t, 10 –6 (C)	0	1	2	3	4	5	6	7	8	9
q, 10 –9 (Кл)	2	1,5	0	–1,5	–2	–1,5	0	1,5	2	1,5

1. Напишите уравнение зависимости заряда от времени. Найдите амплитуду колебаний заряда, период, циклическую частоту, линейную частоту.

2. Какова энергия магнитного поля катушки в момент времени t = 5 мкс, если емкость конденсатора 50 пФ.

Домашнее задание. Напишите уравнение зависимости силы тока от времени. Найдите амплитуду колебаний силы тока. Постройте графическую зависимость силы тока от времени.