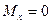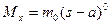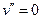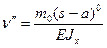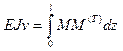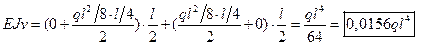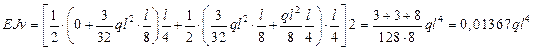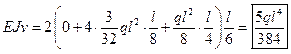Уравнение изгибающих моментов составляется с помощью правил клебша

Правила Клебша сводятся к следующему.

1) выражаем через внешние силы, которые лежат только слева (или только справа) от сечения.

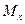
2) Если погонная сила q не доходит до правого конца, то ее доводим до этого правого конца и уравновешиваем ее снизу (рис.16.9)

3) Если имеется сосредоточенный момент m_о, то его вклад записываем в виде 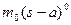, где а — расстояние до момента m_о.

4) Интегрируем, не раскрывая скобок.

При выполнении этих условий все константы С на разных участках будут одинаковы. Аналогично будут одинаковы все константы D.

Справедливость правил Клебша доказывается непосредственной проверкой, то есть подстановкой решения в условия стыковки решения на границе участков. Рассмотрим, например, случай, приведенный на рис.16.12.

По правилам Клебша момент 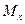на участках (1), (2) запишем в виде:

(1):

(2):

Дифференциальные уравнения на участках:

(1)

(2)

Решение этих уравнений на участках (1), (2) имеет вид:

Участок (1): .

Участок (2): .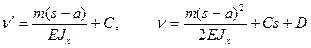

Отсюда видно, что при S = a получим равенство углов наклона и прогибов, вычисленных по разным формулам при любых С и D, т.е. условия гладкости изогнутой оси выполняются. Аналогично проверяются условия гладкости на границе участка, на которой заканчивается погонная сила q.

16.2.3 Условия для определения С и D

1) Первый случай .Рассмотрим балку, лежащую на двух опорах (см. рис.16.10).

Рис. 16.10

Рис. 16.11

Из схемы видно, что

(16.13)

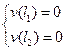
Таким образом, получаем систему уравнений для С и D.

2) Второй случай. Пусть балка заделана на расстоянии 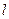(консольная балка, см. рис.16.10).

В заделке не может появиться наклона оси, поэтому там не только нет прогиба, но и .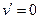

Таким образом, из схемы следует, что:

(16.14)

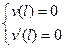
Опять получили два уравнения для С и D.

Пример вычисления прогиба

Пусть необходимо вычислить прогиб в центре балки длины l, загруженной погонной силой q. Решим эту задачу двумя способами.

Ввиду симметричности схемы можно сразу найти реактивные силы – они будут равны ql/2. Тогда изгибающий момент в сечении на расстоянии z от левой опоры будет равен

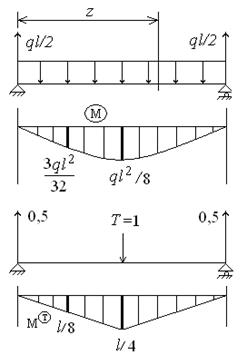Первый способ. Использование дифференциального уравнения изогнутой оси балки. 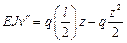Интегрируем 2 раза: Константы интегрирования находим из условий закрепления: 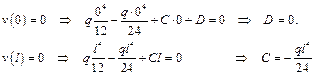Находим прогиб в центре балки (при z = l/2):

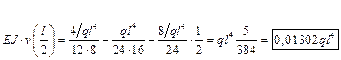Второй способ. Использование интеграла Мора

Прогиб в центре балки находим по формуле

Нарисуем эпюру изгибающих моментов М ( T ) от единичной силы Т=1 (см. рис.2)

Рассмотрим различные приближенные методы интегрирования.

1. Метод трапеций по 2-м участкам.

Метод дал ошибку в 17%

2. Метод трапеций по 4-м участкам.

Метод дал ошибку в 5%

3. Метод Симпсона по 2-м участкам.

Таким образом, метод Симпсона в этом примере дает точное решение.

Дата добавления: 2015-08-11 ; просмотров: 2784 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Правило знаков для поперечных силСкачать

Метод начальных параметров. Универсальное уравнение упругой линии балки

В отличие от предыдущего метода в предлагаемом методе начальных параметров (МНП) независимо от количества силовых участков балки приходится находить только две произвольные постоянные интегрирования – прогиб и угол поворота в начале координат (y₀, θ₀). Это достигается путем применения следующих правил при составлении уравнения моментов:

— начало координат выбирается в одном из крайних сечений балки и является общим для всех ее участков;

— внешний сосредоточенный момент М включается в уравнение изгибающих моментов в виде произведения на множитель вида (z – а) 0 , равный единице (здесь а – абсцисса сечения, где действует внешний момент М);

— в случае завершения действия распределенной нагрузки на некотором участке, ее продолжают до конца рассматриваемого участка, а для обеспечения исходного равновесия вводят “компенсирующую” нагрузку обратного направления;

— операции интегрирования или дифференцирования уравнений на всех участках следует выполнять, применяя прием Клебша, т.е. не раскрывая скобок.

С учетом названных правил составляется и решается ДУУЛБ применительно к заданной расчетной схеме балки. Тогда в конечном виде для балки, имеющей большое количество участков с различными внешними нагрузками, общее универсальное уравнение упругой линии балки (УУУЛБ) будет следующим:

После дифференцирования (2.15) получают универсальное уравнение углов поворота балки (УУУПБ)

где y₀, θ₀ – геометрические начальные параметры, т.е. прогиб и угол поворота в начале координат; определяются из граничных условий;

М₀, Q₀ – статические начальные параметры, т.е. изгибающий момент и поперечная сила в начале координат; они определяются по схеме нагружения балки или из уравнений ее равновесия;

M_i, F_i, q_i – момент, сосредоточенная сила и распределенная нагрузка в i-м сечении балки соответственно; они включаются в уравнение со своими знаками в соответствии с «правилом зонтика» для изгибающего момента;

k_i – величина, характеризующая неравномерно распределенную нагрузку, например, треугольную или трапециевидную; определяется как тангенс угла наклона неравномерной нагрузки, k = tg a ;

Рассмотрим общий порядок определения перемещений методом начальных параметров на примере расчетной схемы некоторой балки (рисунок 2.7), который сводится к следующему:

1 Выбирается начало координат в одном из крайних сечений балки (лучше в левом), которое является общим для всех участков.

2 Для последнего силового участка балки составляется универсальное уравнение упругой линии балки (УУУЛБ)

3 Определяются начальные параметры УУУЛБ:

— геометрические начальные параметры

-статические начальные параметры определяются из уравнений равновесия

4 Все найденные начальные параметры подставляются в исходное УУУЛБ:

путем дифференцирования которого получают универсальное уравнение углов поворота балки (УУУПБ)

5 Определяются искомые перемещения точек балки путем подстановки в соответствующее уравнение числовых значений абсцисс заданных точек. При этом отбрасываются те слагаемые соответствующих универсальных уравнений, которые учитывают внешние нагрузки, приложенные за пределами рассматриваемого участка.

Изложенный выше метод начальных параметров является достаточно простым и универсальным, т.к. позволяет находить линейные и угловые перемещения любых точек балки, с большим количеством силовых участков и с разнообразной нагрузкой. Однако этот метод имеет следующие недостатки:

— он не применим для балок с ломаной осью, рамных систем и кривых брусьев;

— он не позволяет определять перемещения точек балки в произвольных направлениях, не считая вертикального.

Для устранения этих недостатков в курсе сопротивления материалов широко применяются так называемые энергетические способы.

Дата добавления: 2015-02-10 ; просмотров: 300 ; Нарушение авторских прав

Видео:Определение реакций опор в балке. Сопромат.Скачать

Метод начальных параметров

Рассмотренный выше способ определения перемещений в балках при изгибе простым интегрированием приближенных дифференциальных уравнений упругой линии предполагает

написание уравнений изгибающих моментов М_х = f(z) для каждого грузового участка балки, а при их интегрировании требует вычисления постоянных интегрирования С и D на каждом участке.

Если балка имеет п грузовых участков, то необходимо составить п дифференциальных уравнений упругой линии, а после их интегрирования вычислить 2п неизвестных постоянных

интегрирования С и D.

Для определения 2п неизвестных постоянных нужно составить 2п уравнений, которые можно получить из опорных и граничных условий:

• — два опорных условия (рассмотрены выше);
• — граничные условия предполагающие, что на каждой границе между сопряженными участками (при z_m = z_m+1):
• — угол поворота сечения в_т предыдущего участка балки равен углу поворота сечения д_т+1 последующего участка по условию плавности сопряжения упругой линии, т.е. в_т = в_т+1;
• — прогиб у_т предыдущего участка балки равен прогибу у_т+₁последующего участка по условию неразрывности упругой линии на границах сопряжённых участков, т.е. у_т = у_т+

Если число грузовых участков равно п, то между участками будет (п-1) границ, а число граничных условий будет равно 2(п-1). Добавим к ним 2 условия на опорах, получим 2п условий. Подставив 2п условий в 2п уравнений (для прогибов и углов поворота) и решив их, можно найти постоянные интегрирования С и D для каждого грузового участка.

При числе грузовых участков больше двух задача составления уравнений изгибающих моментов М_х = /(z) и вычисления постоянных интегрирования С и D на каждом участке весьма трудоёмкая, что ограничивает на практике применение способа определения перемещений в балках прямым интегрированием дифференциальных уравнений упругой линии.

Рациональным методом составления и интегрирования приближённого дифференциального уравнения упругой линии балки с большим числом грузовых участков является метод уравнивания постоянных интегрирования — метод начальных параметров. Этот метод позволяет независимо от числа грузовых участков свести число постоянных интегрирования к двум С и D, равным

где Е]_х — жёсткости балки; в₀ и у₀ — угол поворота сечения и прогиб в начале координат, т.е. начальные параметры.

Метод начальных параметров значительно упрощает вычисление перемещений в упругих системах (например, в балках) с большим числом грузовых участков.

Для уравнивания постоянных интегрирования С и D на всех участках необходимо использовать следующие приёмы при написании и интегрировании приближённого дифференциального уравнения упругой линии (правила Клебша).

• 1. Начало координат выбирают общим для всех участков и помещают в крайнюю точку продольной оси балки.
• 2. Выражение изгибающего момента M_xi = для

произвольного сечения составляется с учётом внешних нагрузок (.M,P,q), приложенных между началом координат и данным сечением. При этом слагаемые выражения изгибающего момента предыдущих участков сохраняются неизменными и для последующих участков.

• 3. Все слагаемые изгибающего момента, вводимые в уравнение моментов M_xi = /(Zj), должны содержать многочлены вида (z — а_;), где dj — расстояние от начала координат до точки приложения внешнего силового фактора — М, Р, q и т.д. (т.е. a_m,a_P, а_Як и т.д.).
• 4. Если среди нагрузок встречается сосредоточенный момент М, то его следует умножить на множитель (z — а_т)° = 1, т.е. должен быть член М ? (z — а_ш)°, где а_т — расстояние от начала координат до сечения, в котором приложен этот момент.
• 5. Если среди нагрузок встречается распределённая нагрузка q, не доходящая до конца балки, то её следует продлить до конца балки по тому же закону, а добавленную нагрузку компенсировать равной по величине нагрузкой обратного направления.
• 6. Уравнения составляются последовательно для всех участков балки.
• 7. Интегрирование уравнений следует проводить, не раскрывая скобок.

При соблюдении этих правил число постоянных интегрирования сводится к двум С и D, одинаковым для всех грузовых участков и равных

Для определения двух постоянных интегрирования С и D достаточно двух опорных условий, рассмотренных выше.

Для того чтобы найденные постоянные интегрирования С и D были учтены на любом участке, их записывают не в конце, а в начале составленных уравнений для определения углов поворота сечений (2.7) и прогибов (2.8).

При соблюдении правил Клебша в исходном дифференциальном уравнении выражение М_х = /(z), составленное для каждого

последующего участка, целиком включает все члены предыдущего участка, а последний член при значении граничной абсциссы обращается в нуль. При этом для удобства использования полученных уравнений в практических расчетах вводят прерыватели вида |_х (вертикальная черта с номером участка), показывающие, на каком члене следует оборвать уравнение прогибов (или углов поворота) при вычислении этих величин на конкретном участке. Все следующие за чертой слагаемые необходимо отбросить.

Рассмотрим балку постоянного сечения, которая нагружена сосредоточенным моментом М, силой Р и равномерно распределенной нагрузкой интенсивностью q (рис.2.5).

Рис. 2.5. Схема нагружения балки при расчете на изгиб

• 1. Выбираем начало координат в крайней левой точке А продольной оси балки и разбиваем балку на пять участков. На четвёртом участке действует распределённая нагрузка, не доходящая до конца балки. Продлеваем её до конца балки, а добавленную нагрузку компенсируем нагрузкой обратного направления.
• 2. Составляем приближённое дифференциальное уравнение упругой линии (2.6), соблюдая правила Клебша,

и дважды интегрируем полученное уравнение без раскрытия скобок

3. После первого интегрирования уравнения (2.13) получим уравнение углов поворота поперечных сечений балки

4. После интегрирования уравнения (2.14) получим уравнение прогибов балки

Если к элементу конструкции приложено несколько одноименных нагрузок (М_ь Р_ь q^, то дифференциальные уравнения для определения углов поворота поперечных сечений в и прогибов у для упругих систем будет иметь вид

При написании этих уравнений внешние силовые факторы (М, Р, q) записываются в последовательности их приложения к упругой системе (балке) от начала координат и берутся под знаком суммы (Z) со своими алгебраическими знаками (+) или (-) в соответствии с правилами знаков для внутренних изгибающих моментов М_х = /(z) при построении эпюр.

Если при расчете упругой системы начало координат выбрано слева, то правило знаков для перемещений в и у остаются такими же, как и при определении перемещений непосредственным интегрированием, рассмотренным ранее, т.е. при в > 0, то поворот сечения произошёл против часовой стрелки, при в 0), вычисленное по формуле (2.16), означает поворот поперечного сечения балки по часовой стрелке и наоборот, отрицательное значение угла (б Требуется:

• 1) построить эпюры Q и М_х, найти М_тах;
• 2) подобрать деревянную балку круглого поперечного сечения при [а] = 8 МПа ;
• 3) определить прогиб свободного конца.

1. Определяем реактивный момент заделки М_А по формуле

2. Составляя сумму моментов всех сил на ось у, определяем реакцию опоры R_A по формуле

3. Составляем выражения для Q и М_х, вычисляем их значения на границах участков, заносим в таблицу и строим эпюры Q и М_х.

_ Таблица 2Л. Значения Q и М_х для построения эпюр_

№ участка и пределы изменения координаты “z”

🌟 Видео

ЗАПОМНИ ТРИ ГЛАВНЫХ ПРАВИЛА и ты сможешь удивить своего препода по сопромату!Скачать

Определение опорных реакций балки. Сопромат для чайников ;)Скачать

Построение эпюр поперечных сил и изгибающих моментов в балке.Скачать

Построение эпюр в балке ( Q и M ). СопроматСкачать

Правило знаков для изгибающих моментовСкачать

БАЛКА - 90 СТУДЕНТОВ САМОСТОЯТЕЛЬНО СТРОЯТ ЭПЮРЫ после просмотра этого видео!Скачать

Учимся видеть нормальные и касательные напряжения. (Сопромат - Тайные Знания 2).Скачать

Сопротивление материалов. Занятие 10. Часть 1. Расчет статически неопределимой балки.Скачать

Уравнение трех моментов. Расчет много пролетной не разрезной балкиСкачать

Сопротивление материалов. Лекция: универсальное уравнение изогнутой оси балкиСкачать

Определение экстремума эпюры моментов MСкачать

Понимание напряжений в балкахСкачать

Построение эпюр в консольной балкеСкачать

Определение опорных реакций в простой балке. Урок №1Скачать

Построение эпюр поперечных сил и изгибающих моментов в многопролетных шарнирно-консольных балках.Скачать

Как Проводить Простую и Эффективную Медитацию: Глубокое СпокойствиеСкачать

Правило знаков при крученииСкачать

Эпюры M и Q в балке ➤ Построение эпюр моментов и поперечных сил ➤ СопроматСкачать