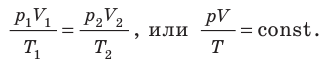Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- Уравнение Клапейрона-Менделеева (уравнение состояния идеального газа).
- Конспект по теме «Уравнение Клапейрона-Менделеева»
- 🎦 Видео
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 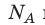
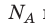
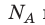
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
Уравнение Клапейрона
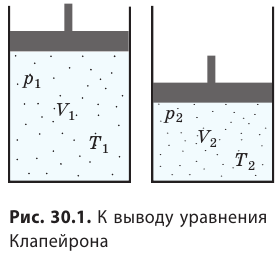
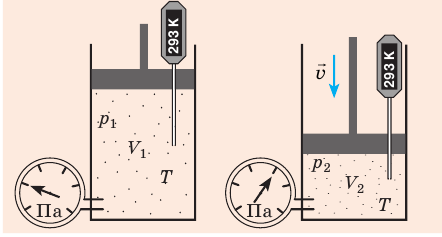
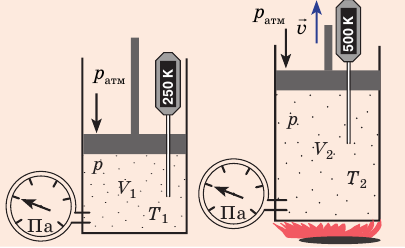
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (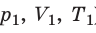
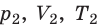
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 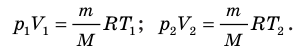
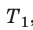
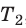
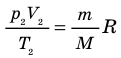
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (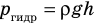
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (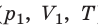
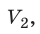
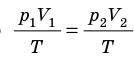
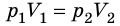
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 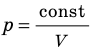
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (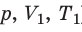
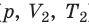
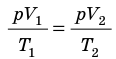
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
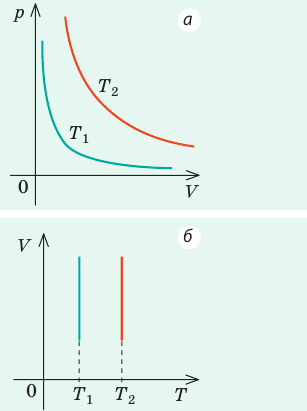
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (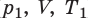
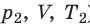
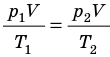
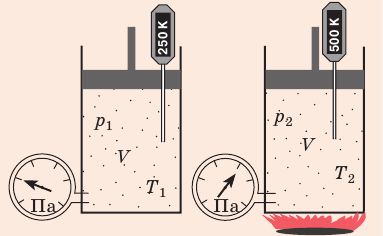
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 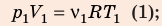
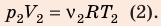

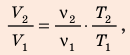
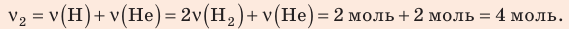
Ответ: примерно в 2,7 раза.
Пример №2
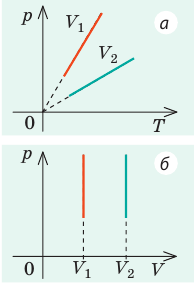
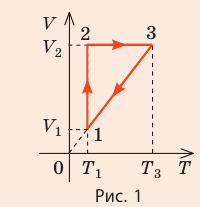
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
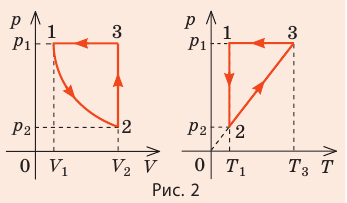
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

Уравнение Клапейрона-Менделеева (уравнение состояния идеального газа).
Уравнение Клапейрона-Менделеева (1834 г) устанавливает связь между объемом V, давлением P и абсолютной температурой Т для газа:
n – число молей газа 
P – давление газа, Па;
V – объем газа, м 3 ;
T – абсолютная температура газа, К;
R – универсальная газовая постоянная 8,314 Дж/моль×K.
Если объём газа выражен в литрах, то уравнение Клапейрона-Менделеева записывается в виде:
Из уравнения Клапейрона-Менделеева следует три закона:
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Конспект по теме «Уравнение Клапейрона-Менделеева»
Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.
«Актуальность создания школьных служб примирения/медиации в образовательных организациях»
Свидетельство и скидка на обучение каждому участнику
№24. Уравнение Клапейрона-Менделеева. Уравнение состояния идеального газа. Молярная газовая постоянная.
Объединенный газовый закон.
Макроскопические величины, однозначно характеризующие состояние газа, называют термодинамическими параметрами газа.
Важнейшими термодинамическими параметрами газа являются его объем V, давление р и температура Т.
Всякое изменение состояния газа называется термодинамическим процессом.
В любом термодинамическом процессе изменяются параметры газа, определяющие его состояние.
Соотношение между значениями тех или иных параметров в начале и конце процесса называется газовым законом .
Газовый закон, выражающий связь между всеми тремя параметрами газа называется объединенным газовым законом.
Соотношение p = nkT связывающее давление газа с его температурой и концентрацией молекул, получено для модели идеального газа, молекулы которого взаимодействуют между собой и со стенками сосуда только во время упругих столкновений. Это соотношение может быть записано в другой форме, устанавливающей связь между макроскопическими параметрами газа – объемом V, давлением p, температурой T и количеством вещества ν. Для этого нужно использовать равенства
где n – концентрация молекул, N – общее число молекул, V – объем газа
Тогда получим 
Так как при постоянной массе газа N остается неизменным, то Nk – постоянное число, значит
При постоянной массе газа произведение объема на давление, деленное на абсолютную температуру газа, есть величина одинаковая для всех состояний этой массы газа.
Уравнение, устанавливающее связь между давлением, объемом и температурой газа было получено в середине XIX века французским физиком Б. Клапейроном и часто его называют уравнением Клапейрона.
Уравнение Клапейрона можно записать в другой форме.
Здесь N – число молекул в сосуде, ν – количество вещества, NА – постоянная Авогадро, m – масса газа в сосуде, M – молярная масса газа. В итоге получим:
Произведение постоянной Авогадро NА на постоянную Больцмана k называется универсальной (молярной) газовой постоянной и обозначается буквой R.
Ее численное значение в СИ R = 8,31 Дж/моль·К
называется уравнением состояния идеального газа.
В полученной нами форме оно было впервые записано Д. И. Менделеевым. Поэтому уравнение состояния газа называется уравнением Клапейрона–Менделеева.`
Для одного моля любого газа это соотношение принимает вид: pV=RT
Установим физический смысл молярной газовой постоянной. Предположим, что в некотором цилиндре под поршнем при температуре T находится 1 моль газа, объем которого V. Если нагреть газ изобарно (при постоянном давлении) на 1 К, то поршень поднимется на высоту Δh, а обьем газа увеличится на ΔV.
Запишем уравнение pV=RT для нагретого газа: p (V + ΔV ) = R (T + 1)
и вычтем из этого равенства уравнение pV=RT , соответствующее состоянию газа до нагревания. Получим pΔV = R
ΔV = SΔh, где S – площадь основания цилиндра. Подставим в полученное уравнение:
pS = F – сила давления.
Получим FΔh = R, а произведение силы на перемещение поршня FΔh = А – работа по перемещению поршня, совершаемая этой силой против внешних сил при расширении газа.
Таким образом, R = A.
Универсальная (молярная) газовая постоянная численно равна работе, которую совершает 1 моль газа при изобарном нагревании его на 1 К.
Из уравнения состояния вытекает связь между давлением, объемом и температурой идеального газа, который может находиться в двух любых состояния.
Если индексом 1 обозначить параметры, относящиеся к первому состоянию, а индексом 2 – ко второму состоянию, то согласно уравнению состояния для газа данной массы



Правые части равны, следовательно, равны и левые


Это уравнение называется уравнением Клапейрона
Процессы, при которых один из параметров состояния газа остается постоянным называют изопроцессами.
Газовые законы – это законы, описывающие изопроцессы в идеальном газе.
Газовые законы были открыты экспериментально, но все они могут быть получены из уравнения Менделеева-Клапейрона.
Рассмотрим каждый из них.
Изотермический процесс – процесс перехода идеального газа из одного состояния в другое без изменения температуры.
Закон, описывающий связь между параметрами газа при таком процессе, называется закон Бойля-Мариотта в честь двух учёных, практически одновременно выведших его: англичанина Роберта Бойля и француза Эдма Мариотта (рис. 2). Запишем его:
Получаем: 

Из этого закона, очевидно, следует обратно пропорциональная связь давления и объёма: при увеличении объёма наблюдается уменьшение давления, и наоборот. График зависимости меняющихся величин в уравнении, то есть P и V, имеет следующий вид и называется изотермой:
Разным постоянным температурам соответствуют различные температуры.
Изотермическим процессом приближенно можно считать процесс медленного сжатия воздуха или расширение газа под поршнем насоса при откачке его из сосуда.
Изобарный (или изобарический) процесс – процесс перехода идеального газа из одного состояния в другое при постоянном значении давления.
Впервые такой процесс рассмотрел французский учённый Жозеф-Луи Гей-Люссак, поэтому закон носит его имя.
Получаем: 

Из этого закона очевидно следует прямо пропорциональная связь между температурой и объёмом: при увеличении температуры наблюдается увеличение объёма, и наоборот. График зависимости меняющихся величин в уравнении, то есть T и V, имеет следующий вид и называется изобарой
Следует обратить внимание на то, что работая с абсолютной шкалой температур, на графике присутствует область, близкая к абсолютному нулю температур, в которой данный закон не выполняется. Поэтому прямую в области, близкой к нулю, следует изображать пунктирной линией.
Изохорный (или изохорический) процесс – процесс перехода идеального газа из одного состояния в другое при постоянном значении объёма .
Процесс рассмотрен впервые французом Жаком Шарлем, поэтому закон носит его имя. Запишем закон Шарля:
Получаем: 

Из этого закона очевидно следует прямо пропорциональная связь между температурой и давлением: при увеличении температуры наблюдается увеличение давления, и наоборот. График зависимости меняющихся величин в уравнении, то есть T и P, имеет следующий вид и называется изохорой
В районе абсолютного нуля для графиков изохорного процесса также существует лишь условная зависимость, поэтому прямую также следует доводить до начала координат пунктиром.
Стоит обратить внимание, что именно такая зависимость температуры от давления и объёма при изохорных и изобарных процессах соответственно определяет эффективность и точность измерения температуры с помощью газовых термометров.
Интересен также тот факт, что исторически первыми были открыты именно изопроцессы, которые, как мы показали, являются частными случаями уравнения состояния, а уже потом уравнения Клапейрона и Менделеева-Клапейрона. Хронологически сначала были исследованы процессы, протекающие при постоянной температуре, затем при постоянном объёме а последними – изобарические процессы.
Теперь для сравнения всех изопроцессов мы собрали их в одну таблицу Обратите внимание, что графики изопроцессов в координатах, содержащих неизменяющийся параметр, собственно говоря, и выглядят как зависимость константы от какой-либо переменной.
До какой температуры нужно изобарически охладить некоторую массу газа с начальной температурой 37º C , чтобы объем газа уменьшился при этом на одну четверть?
Изобарный процесс описывается законом Гей-Люссака:
Газ нужно охладить до температуры 233К
В закрытом сосуде находится газ под давлением 200 кПа. Каким станет давление газа, если температуру повысить на 30%?
Так как сосуд с газом закрытый, объем газа не меняется. Изохорный процесс описывается законом Шарля:
Ответ Давление газа станет равным 260 кПа.
Задание 3 Представить этот цикл в координатах ( p , T ) и ( V , T )
* Как будет выглядеть график данного процесса в координатах P-V?
🎦 Видео
Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Урок 194. Уравнение Ван-дер-ВаальсаСкачать

Идеальный газ в молекулярно-кинетической теории | Физика 10 класс #28 | ИнфоурокСкачать

Уравнение состояния идеального газаСкачать

Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Уравнение идеального газа: PV = nRT | Газы.Молекулярно-кинетическая теория | Химия (видео 1)Скачать

29. Адиабатический процесс. Уравнение ПуассонаСкачать

Уравнение состояния идеального газаСкачать

Физика. МКТ: Уравнение Менделеева-Клапейрона для идеального газа. Центр онлайн-обучения «Фоксфорд»Скачать

идеальный газ УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗАСкачать

Физика 10 класс (Урок№18 - Основное уравнение МКТ.)Скачать

Физика. 10 класс. Уравнение состояния идеального газа /23.11.2020/Скачать

Физика 10 Идеальный газ Основное уравнение МКТ идеального газа Решение задачСкачать

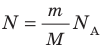
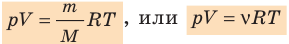
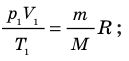
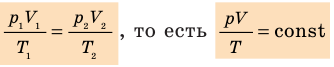
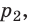
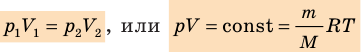

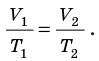
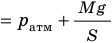
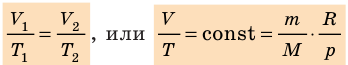
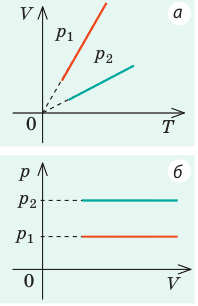

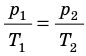
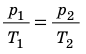
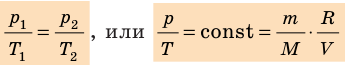

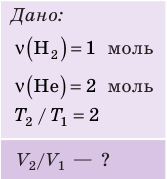
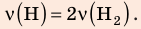

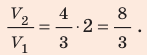
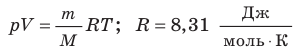 — универсальная газовая постоянная.
— универсальная газовая постоянная.