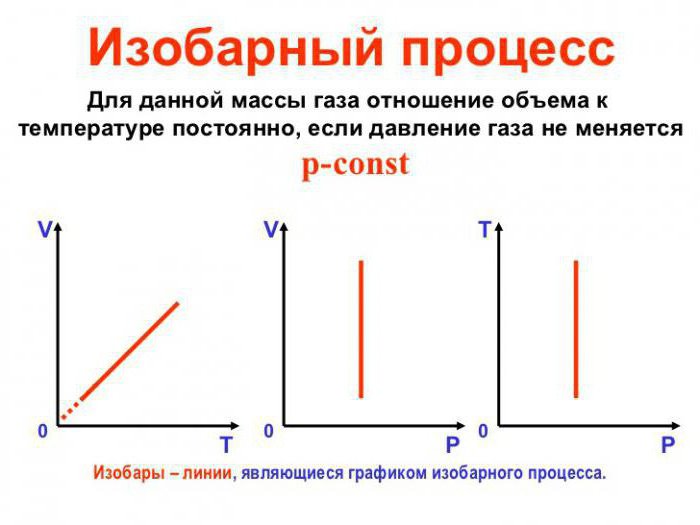
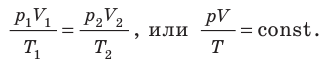Изобарный процесс (также называемый изобарическим процессом) является одним из термодинамических процессов, которые происходят при постоянном показателе давления. Масса газа системы при этом также остается постоянной. Наглядное представление о графике, демонстрирующем изобарный процесс, дает термодинамическая диаграмма в соответствующей системе координат.
- Примеры
- Обратимость
- Вывод закона Гей-Люссака (первичное понимание)
- Получение универсальной газовой постоянной
- Уравнение Менделеева-Клапейрона
- Работа газа при изобарном процессе
- Универсальная газовая постоянная и ее смысл
- Заключение
- Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
- Уравнение состояния идеального газа
- Уравнение Клапейрона
- Изопроцессы
- Какой процесс называют изотермическим. Закон Бойля — Мариотта
- Какой процесс называют изобарным. Закон Гей-Люссака
- Закон Гей-Люссака
- Изохорный процесс. Закон Шарля
- Закон Шарля
- Пример №1
- Пример №2
- Уравнение состояния идеального газа. Изопроцессы
- 🎥 Видео
Видео:Эта тема ВСЕГДА встречается на экзамене ЦТ — Изопроцессы (Физика для чайников)Скачать

Примеры
Наиболее простым примером изобарического процесса можно назвать нагревание некоторого объема воды в открытом сосуде. В качестве еще одного примера можно привести расширение идеального газа в цилиндрическом объеме, где поршень имеет свободный ход. В каждом из этих случаев давление будет постоянным. Оно равно обыкновенному атмосферному давлению, что вполне очевидно.
Видео:Уравнение состояния идеального газа. 10 класс.Скачать

Обратимость
Изобарный процесс можно считать обратимым в том случае, если давление в системе совпадает с внешним давлением и равно во все моменты времени процесса (то есть оно постоянно по своему значению), а температура изменяется очень медленно. Таким образом, термодинамическое равновесие в системе сохраняется в каждый момент времени. Именно совокупность вышеперечисленных факторов дает нам возможность считать изобарный процесс обратимым.
Чтобы осуществить в системе изобарический процесс, теплоту к ней нужно или подводить, или отводить. При этом теплота должна расходоваться на работу расширения идеального газа и на изменение его внутренней энергии. Формулу, демонстрирующую зависимость величин друг от друга при изобарном процессе, называют законом Гей-Люссака. Она показывает, что объем пропорционален температуре. Давайте выведем эту формулу на основании поверхностных знаний.
Видео:Физика 10 класс (Урок№20 - Уравнение состояния идеального газа. Газовые законы.)Скачать

Вывод закона Гей-Люссака (первичное понимание)
Человек, хотя бы немного разбирающийся в молекулярной физике, знает, что многие задачи связаны с определенными параметрами. Имя им – давление газа, объем газа и температура газа. В тех или иных случаях в ход идут молекулярная и молярная масса, количество вещества, универсальная газовая постоянная и другие показатели. И здесь есть определенная связь. Давайте поговорим об универсальной газовой постоянной подробнее. На тот случай, если кто-то не знает, каким образом ее получили.
Видео:Уравнение состояния идеального газа | Физика 10 класс #33 | ИнфоурокСкачать

Получение универсальной газовой постоянной
Эту константу (постоянное число с определенной размерностью) принято также называть постоянной Менделеева. Она присутствует также в уравнении Менделеева-Клапейрона для идеального газа. Как же получил наш знаменитый физик эту константу?
Как мы знаем, уравнение идеального газа имеет следующую форму: PV/T (что озвучивается так: “произведение давления на объем, деленное на температуру”). По отношению к универсальной газовой постоянной применим так называемый закон Авогадро. Он гласит о том, что если мы возьмем любой газ, то одинаковое его количество молей при одинаковой температуре и одинаковом давлении займет одинаковый объем.
По сути дела, это есть словесная формулировка уравнения состояния идеального газа, которое было записано в виде формулы немного ранее. Если мы возьмем нормальные условия (а это когда температура газа равна 273,15 Кельвинов, давление равно 1 атмосфере, соответственно, 101325 Паскалей, а объем моля газа равен 22,4 литра) и подставим их в уравнение, все перемножим и разделим, то получим, что совокупность подобных действий дает нам численный показатель, равный 8,31. Размерность дается в Джоулях, деленных на произведение моля на Кельвин (Дж/моль*К).
Видео:Урок 156. Уравнение состояния идеального газа. Квазистатические процессыСкачать

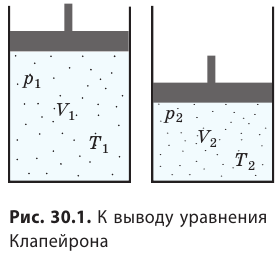
Уравнение Менделеева-Клапейрона
Давайте возьмем уравнение состояния идеального газа и перепишем его в новом виде. Изначальное уравнение, напомним, имеет вид PV/T=R. А теперь умножим обе части на температурный показатель. Получим формулу PV(м)=RT. То есть произведение давления на объем равно произведению универсальной газовой постоянной на температуру.
Теперь умножим обе части уравнения на то или иное количество молей. Обозначим их количество буквой, скажем, X. Таким образом, получим следующую формулу: PV(м)X=XRT. Но ведь мы знаем, что произведение V с индексом “м” дает нам в результате просто объем V, а число молей X раскрывается в виде деления частной массы на молярную массу, то есть имеет вид m/M.
Таким образом, конечная формула будет выглядеть следующим образом: PV=MRT/m. Это и есть то самое уравнение Менделеева-Клапейрона, к которому пришли оба физика практически одновременно. Мы можем умножить правую часть уравнения (и в то же время разделить) на число Авогадро. Тогда получим: PV = XN(a)RT/N(a). Но ведь произведение количества молей на число Авогадро, то есть XN(a), дает нам не что иное, как общее число молекул газа, обозначаемое буквой N.
В то же время частное от универсальной газовой постоянной и числа Авогадро – R/N(a) даст постоянную Больцмана (обозначается k). В итоге мы получим еще одну формулу, но уже в несколько другом виде. Вот она: PV=NkT. Можно раскрыть эту формулу и получить следующий результат: NkT/V=P.
Видео:мкт ИЗОТЕРМИЧЕСКИЙ процесс ИЗОХОРНЫЙ процесс ИЗОБАРНЫЙ процессСкачать

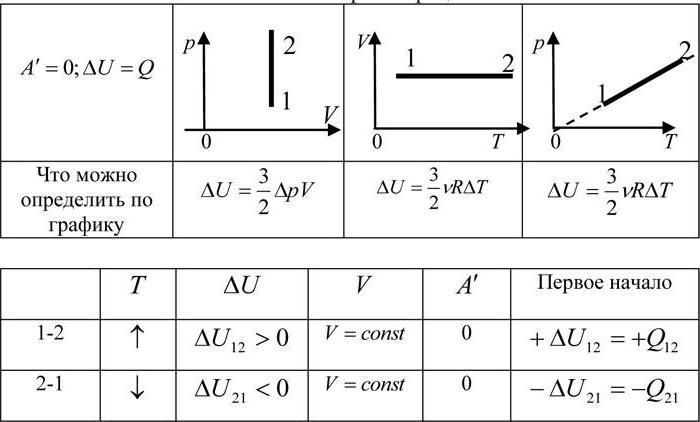
Работа газа при изобарном процессе
Как мы выяснили ранее, изобарным процессом называется термодинамический процесс, при котором давление остается величиной постоянной. А чтобы выяснить, как будет определяться работа при изобарном процессе, нам придется обратиться к первому началу термодинамики. Общая формула выглядит следующим образом: dQ = dU + dA, где dQ — это количество теплоты, dU – изменение внутренней энергии, а dA – работа, совершаемая в ходе выполнения термодинамического процесса.
Теперь рассмотрим конкретно изобарный процесс. Примем во внимание тот фактор, что давление остается постоянным. Теперь попытаемся переписать первое начало термодинамики для изобарного процесса: dQ = dU + pdV. Чтобы получить наглядное представление о процессе и работе, нужно изобразить его в системе координат. Ось абсцисс обозначим p, ось ординат V. Пускай объем будет увеличиваться. В двух отличных друг от друга точках с соответствующим значением p (конечно же, фиксированным) отметим состояния, представляющие собой V1 (первоначальный объем) и V2 (конечный объем). В этом случае график будет представлять собой прямую линию, параллельную оси абсцисс.
Найти работы в таком случае проще простого. Это будет просто площадь фигуры, ограниченная с двух сторон проекциями на ось абсцисс, а с третьей стороны – прямой линией, соединяющей точки, лежащие, соответственно, в начале и конце изобарной прямой. Попробуем вычислить значение работы при помощи интеграла.
Он будет вычисляться следующим образом: A = p (интеграл в пределах от V1 до V2) dV. Раскроем интеграл. Получим, что работа будет равна произведению давления на разность объемов. То есть выглядеть формула будет следующим образом: A = p (V2 – V1). Если мы раскроем некоторые величины, то получим еще одну формулу. Она выглядит так: A = xR (T2 – T2), где x – количество вещества.
Видео:Работа, совершаемая при термодинамических процессах. 10 класс.Скачать

Универсальная газовая постоянная и ее смысл
Можно сказать, что последнее выражение будет определять физический смысл R – универсальной газовой постоянной. Чтобы было понятнее, давайте обратимся к конкретным числам. Возьмем для проверки один моль какого-либо вещества. В то же время пускай температурная разница будет составлять 1 Кельвин. В этом случае легко заметить, что работа газа будет равна универсальной газовой постоянной (или же наоборот).
Видео:Урок 157. Изопроцессы и их графики. Частные газовые законыСкачать

Заключение
Этот факт можно подать немного в другом свете, перефразировав формулировку. Например, универсальная газовая постоянная будет численно равна работе, совершаемой при изобарном расширении одним молем идеального газа, если он нагревается на один Кельвин. Вычислить работу при других изопроцессах будет несколько сложнее, но главное — при этом применять логику. Тогда все быстро встанет на свои места, и вывод формулы окажется проще, чем вы думаете.
Видео:Урок 145. Идеальный газ. Основное ур-ние МКТ ид. газа - 1Скачать

Уравнение состояния идеального газа — основные понятия, формулы и определение с примерами
Содержание:
Уравнение состояния идеального газа:
Уравнения Клапейрона и Менделеева — клапейрона; законы Шарля, Гей-Люссака, Бойля — Мариотта, Авогадро, Дальтона, — пожалуй, такого количества «именных» законов нет ни в одном разделе физики. за каждым из них — кропотливая работа в лабораториях, тщательные измерения, длительные аналитические размышления и точные расчеты. нам намного проще. Мы уже знаем основные положения теории, и «открыть» все вышеупомянутые законы нам не составит труда.
Видео:Решение графических задач на тему Газовые законыСкачать

Уравнение состояния идеального газа
Давление газа полностью определяется его температурой и концентрацией молекул: p=nkT. Запишем данное уравнение в виде: pV = NkT. Если состав и масса газа известны, число молекул газа можно найти из соотношения
Произведение числа Авогадро 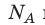
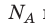
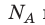
Обратите внимание! Состояние данного газа некоторой массы однозначно определяется двумя его макроскопическими параметрами; третий параметр можно найти из уравнения Менделеева — Клапейрона.
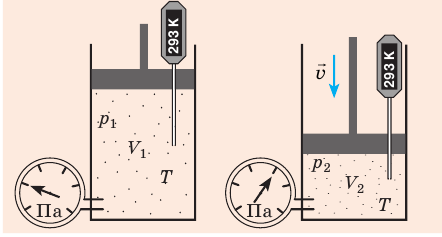
Уравнение Клапейрона
С помощью уравнения Менделеева — Клапейрона можно установить связь между макроскопическими параметрами газа при его переходе из одного состояния в другое. Пусть газ, имеющий массу m и молярную массу М, переходит из состояния (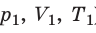
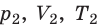
Для каждого состояния запишем уравнение Менделеева — Клапейрона: 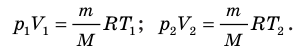
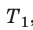
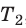
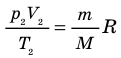
Для данного газа некоторой массы отношение произведения давления на объем к температуре газа является неизменным.
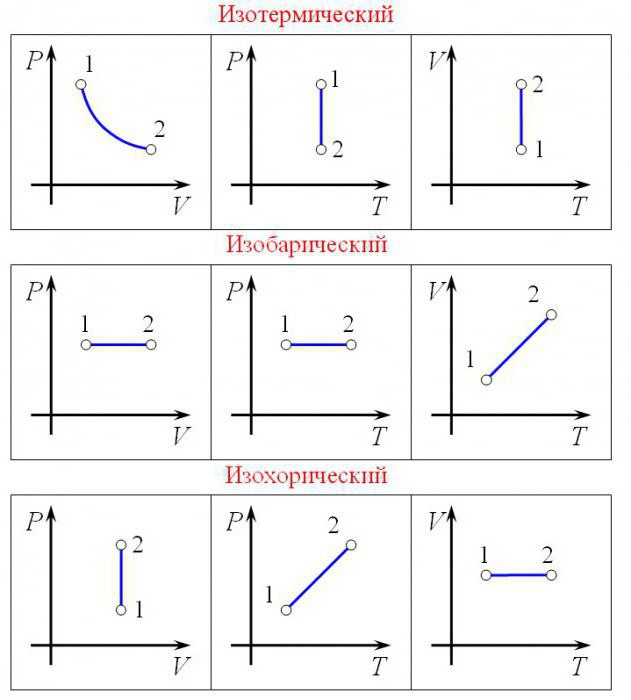
Изопроцессы
Процесс, при котором один из макроскопических параметров данного газа некоторой массы остается неизменным, называют изопроцессом. Поскольку состояние газа характеризуется тремя макроскопическими параметрами, возможных изопроцессов тоже три: происходящий при неизменной температуре; происходящий при неизменном давлении; происходящий при неизменном объеме. Рассмотрим их.
Какой процесс называют изотермическим. Закон Бойля — Мариотта
Пузырек воздуха, поднимаясь со дна глубокого водоема, может увеличиться в объеме в несколько раз, при этом давление внутри пузырька падает, поскольку вследствие дополнительного гидростатического давления воды (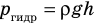
Рис. 30.2. Изотермическое сжатие газа. Если медленно опускать поршень, температура газа под поршнем будет оставаться неизменной и равной температуре окружающей среды. Давление газа при этом будет увеличиваться
Изотермический процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменной температуре.
Пусть некий газ переходит из состояния (
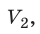
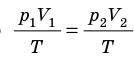
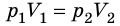
Закон Бойля — Мариотта:
Для данного газа некоторой массы произведение давления газа на его объем остается постоянным, если температура газа не изменяется:
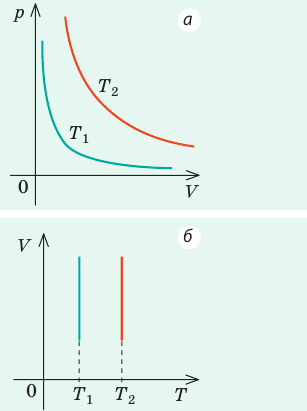
Графики изотермических процессов называют изотермами. Как следует из закона Бойля — Мариотта, при неизменной температуре давление газа данной массы обратно пропорционально его объему: 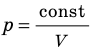
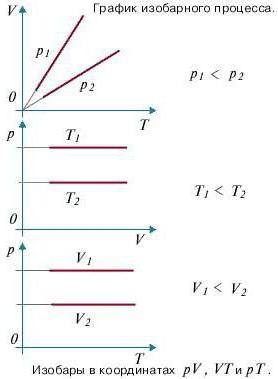
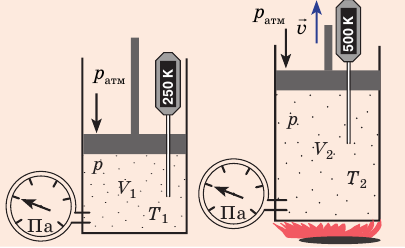
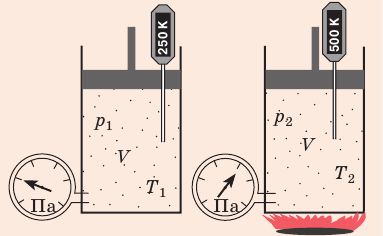
Какой процесс называют изобарным. Закон Гей-Люссака
Изобарный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном давлении.
Пусть некий газ переходит из состояния (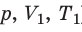
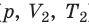
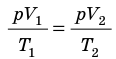
Рис. 30.4. Изобарное расширение газа. Если газ находится под тяжелым поршнем массой M и площадью S, который может перемещаться практически без трения, то при увеличении температуры объем газа будет увеличиваться, а давление газа будет оставаться неизменным и равным p
Закон Гей-Люссака
Для данного газа некоторой массы отношение объема газа к температуре остается постоянным, если давление газа не изменяется:
Графики изобарных процессов называют изобарами. Как следует из закона Гей-Люссака, при неизменном давлении объем газа данной массы прямо пропорционален его температуре: V = const⋅T. График данной зависимости — прямая, проходящая через начало координат (рис. 30.5, а). По графику видно, что с приближением к абсолютному нулю объем идеального газа должен уменьшиться до нуля. Понятно, что это невозможно, поскольку реальные газы при низких температурах превращаются в жидкости. В координатах p, V и p, T изобары перпендикулярны оси давления (рис. 30.5, б, в).
Изохорный процесс. Закон Шарля
Если газовый баллон сильно нагреется на солнце, давление в нем повысится настолько, что баллон может взорваться. В данном случае имеем дело с изохорным нагреванием.
Изохорный процесс — процесс изменения состояния данного газа некоторой массы, протекающий при неизменном объеме.
Пусть некий газ переходит из состояния (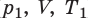
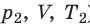
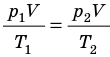
Рис. 30.6. Изохорное нагревание газа. Если газ находится в цилиндре под закрепленным поршнем, то с увеличением температуры давление газа тоже будет увеличиваться. Опыт показывает, что в любой момент времени отношение давления газа к его температуре неизменно:
Закон Шарля
Для данного газа некоторой массы отношение давления газа к его температуре остается постоянным, если объем газа не изменяется:
Графики изохорных процессов называют изохорами. Из закона Шарля следует, что при неизменном объеме давление газа данной массы прямо пропорционально его температуре: p T = ⋅ const . График этой зависимости — прямая, проходящая через начало координат (рис. 30.7, а). В координатах p, V и V, T изохоры перпендикулярны оси объема (рис. 30.7, б, в).
Пример №1
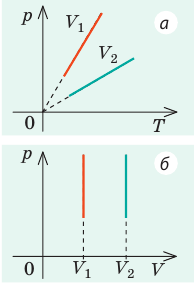
В вертикальной цилиндрической емкости под легкоподвижным поршнем находится 2 моль гелия и 1 моль молекулярного водорода. Температуру смеси увеличили в 2 раза, и весь водород распался на атомы. Во сколько раз увеличился объем смеси газов?
Анализ физической проблемы. Смесь газов находится под легкоподвижным поршнем, поэтому давление смеси не изменяется:
Решение:
Воспользуемся уравнением состояния идеального газа: pV = νRT. Запишем это уравнение для состояний смеси газов до и после распада: 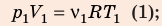
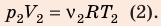

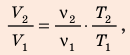
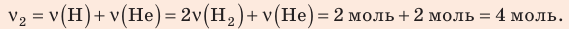
Ответ: примерно в 2,7 раза.
Пример №2
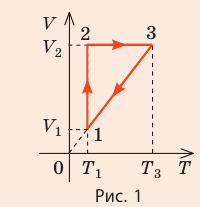
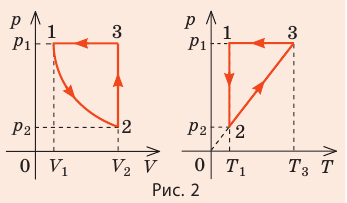
На рис. 1 представлен график изменения состояния идеального газа неизменной массы в координатах V, T. Представьте график данного процесса в координатах p, V и p, T.
Решение:
1. Выясним, какой изопроцесс соответствует каждому участку графика (рис. 1).
Зная законы, которым подчиняются эти изопроцессы, определим, как изменяются макроскопические параметры газа. Участок 1–2: изотермическое расширение; T = const, V ↑, следовательно, по закону Бойля — Мариотта p ↓. Участок 2–3: изохорное нагревание; V = const, T ↑, следовательно, по закону Шарля p ↑ . Участок 3–1: изобарное охлаждение; p = const , T ↓, следовательно, по закону Гей-Люссака V ↓ .
2. Учитывая, что точки 1 и 2 лежат на одной изотерме, точки 1 и 3 — на одной изобаре, а точки 2 и 3 на одной изохоре, и используя результаты анализа, построим график процесса в координатах p, V и p, T (рис. 2)
- Из соотношения p=nkT можно получить ряд важных законов, большинство из которых установлены экспериментально.
- Уравнение состояния идеального газа (уравнение Менделеева — Клапейрона):
— универсальная газовая постоянная.
- Уравнение Клапейрона:
- Законы, которым подчиняются изопроцессы, то есть процессы, при которых один из макроскопических параметров данного газа некоторой массы остается неизменным:
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Температура в физике
- Парообразование и конденсация
- Тепловое равновесие в физике
- Изопроцессы в физике
- Абсолютно упругие и неупругие столкновения тел
- Механизмы, работающие на основе правила моментов
- Идеальный газ в физике
- Уравнение МКТ идеального газа
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Газовые законы. Изопроцессы | Физика 10 класс #34 | ИнфоурокСкачать

Уравнение состояния идеального газа. Изопроцессы
Соотношение p = n k T – это формула, связывающая значение давления газа с его температурой и концентрацией молекул на единицу объема.
Они взаимодействуют со стенками сосуда посредствам упругих соударений. Данное выражение можно записать иначе, учитывая параметрические состояния объема V , давления p , температуры T и количества вещества ν . Применим неравенства:
n = N V = ν N А V = m M N A V .
Значением N является количество молекул данного сосуда, N А – постоянной Авогадро, m – массой газа в емкости, М – молярной массой газа. Исходя из этого, формула примет вид:
p V = ν N А k T = m M N А k T .
Произведение постоянной Авогадро N А на постоянную Больцмана k называют универсальной газовой постоянной и обозначают R .
По системе С И имеет значение R = 8 , 31 Д ж / м о л ь · К .
Соотношение p V = ν R T = m M R T получило название уравнения состояния идеального газа.
Один моль газа обозначается p V = R T .
При температуре T н = 273 , 15 К ( 0 ° C ) и давлении ρ н = 1 а т м = 1 , 013 · 10 5 П а говорят о нормальных условиях состояния газа.
Из уравнения видно, что один моль газа при нормальных условиях занимает один и тот же объем, равный v 0 = 0 , 0224 м 3 / м о л ь = 22 , 4 д м 3 / м о л ь . Выражение получило название закона Авогадро.
Если имеется смесь невзаимодействующих газов, то формулу запишем как:
p V = ν 1 + ν 2 + ν 3 + . . . R T ,
где ν 1 , v 2 , v 3 обозначает количество вещества каждого из них.
Еще в ХХ веке Б. Клапейрон получил уравнение, показывающее связь между давлением и температурой:
p V = ν R T = m M R T .
Впоследствии оно было записано Д.И. Менделеевым. Позже его назвали уравнением Клапейрона-Менделеева.
Задолго до получения уравнения состояния идеального газа на основе молекулярно-кинетической теории поведения газов изучались в различных условиях экспериментально. То есть уравнение p V = ν R T = m M R T служит обобщением всех опытных фактов.
Газ принимает участие в процессах с постоянно изменяющимися параметрами состояния: ( p , V и T ).
При протекании процессов медленно, система находится в состоянии, близком к равновесному. Процесс получил название квазистатического.
Соотнеся с происхождением процессов в нашем времени, то его протекания нельзя считать медленными.
Обычное время для разрежения и сжатия газа сотни раз в секунду. Это рассматривается как квазистатический процесс. Они изображаются с помощью диаграммы состояний параметров, где каждая из точек показывает равновесное состояние.
При неизменном одном параметре из ( p , V или T ) процесс принято называть изопроцессом.
🎥 Видео
Физика - Газовые законы. Уравнение идеального газа.Скачать

Работа при изотермическом процессеСкачать

Урок 172. Применение 1 закона термодинамики для различных процессовСкачать

ЕГЭ. Физика. Уравнение состояния идеального газа. ПрактикаСкачать

Идеальный газ. Основное уравнение молекулярно-кинетической теории газов. 10 класс.Скачать

Уравнение состояния идеального газа. Практическая часть. 10 класс.Скачать

Применение первого закона термодинамики к изопроцессам. 10 класс.Скачать



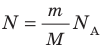
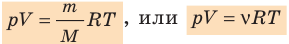
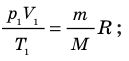
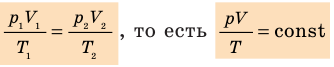
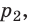
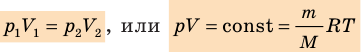

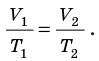
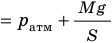
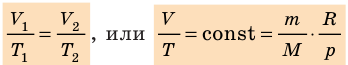
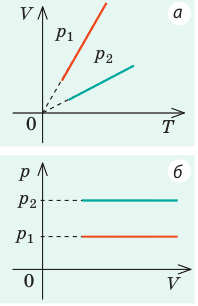

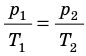
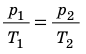
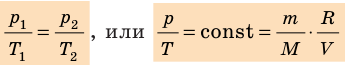

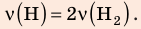

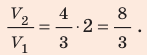
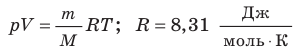 — универсальная газовая постоянная.
— универсальная газовая постоянная.