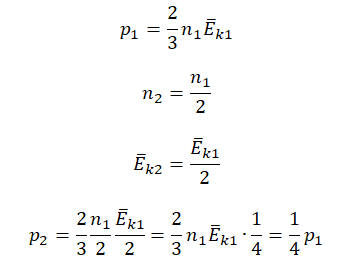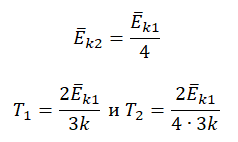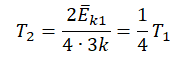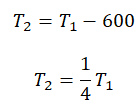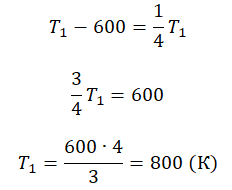Уравнение идеального газа постоянная больцмана

Основное уравнение МКТ идеального газа

теория по физике 🧲 молекулярная физика, МКТ, газовые законы

Идеальный газ — газ, удовлетворяющий трем условиям:

• Молекулы — материальные точки.
• Потенциальная энергия взаимодействия молекул пренебрежительно мала.
• Столкновения между молекулами являются абсолютно упругими.

Реальный газ с малой плотностью можно считать идеальным газом.

Измерение температуры

Температуру можно измерять по шкале Цельсия и шкале Кельвина. По шкале Цельсия за нуль принимается температура, при которой происходит плавление льда. По шкале Кельвина за нуль принимается абсолютный нуль — температура, при котором давление идеального газа равно нулю, и его объем тоже равен нулю.

Обозначение температуры

1. По шкале Цельсия — t. Единица измерения — 1 градус Цельсия (1 o C).
2. По шкале Кельвина — T. Единица измерения — 1 Кельвин (1 К).

Цена деления обеих шкал составляет 1 градус. Поэтому изменение температуры в градусах Цельсия равно изменению температуры в Кельвинах:

При решении задач в МКТ используют значения температуры по шкале Кельвина. Если в условиях задачи температура задается в градусах Цельсия, нужно их перевести в Кельвины. Это можно сделать по формуле:

Если особо важна точность, следует использовать более точную формулу:

Пример №1. Температура воды равна o C. Определить температуру воды в Кельвинах.

T = t + 273 = 2 + 273 = 275 (К)

Основное уравнение МКТ идеального газа

Давление идеального газа обусловлено беспорядочным движением молекул, которые сталкиваются друг с другом и со стенками сосуда. Основное уравнение МКТ идеального газа связывает давление и другие макропараметры (объем, температуру и массу) с микропараметрами (массой молекул, скоростью молекул и кинетической энергией).

Основное уравнение МКТ

Давление идеального газа пропорционально произведению концентрации молекул на среднюю кинетическую энергию поступательного движения молекулы.

p = 2 3 . . n − E k

p — давление идеального газа, n — концентрация молекул газа, − E k — средняя кинетическая энергия поступательного движения молекул.

Выражая физические величины друг через друга, можно получить следующие способы записи основного уравнения МКТ идеального газа:

p = 1 3 . . m 0 n − v 2

m 0 — масса одной молекулы газа;

n — концентрация молекул газа;

− v 2 — среднее значение квадрата скорости молекул газа.

Среднее значение квадрата скорости не следует путать со среднеквадратичной скоростью v, которая равна корню из среднего значения квадрата скорости:

p = 1 3 . . ρ − v 2

ρ — плотность газа

k — постоянная Больцмана (k = 1,38∙10 –3 Дж/кг)

T — температура газа по шкале Кельвина

Пример №2. Во сколько раз уменьшится давление идеального одноатомного газа, если среднюю кинетическую энергию теплового движения молекул и концентрацию уменьшить в 2 раза?

Согласно основному уравнению МКТ идеального газа, давление прямо пропорционально произведению средней кинетической энергии теплового движения молекул и концентрации его молекул. Следовательно, если каждая из этих величин уменьшится в 2 раза, то давление уменьшится в 4 раза:

Следствия из основного уравнения МКТ идеального газа

Через основное уравнение МКТ идеального газа можно выразить скорость движения молекул (частиц газа):

v = √ 3 k T m 0 . . = √ 3 R T M . .

R — универсальная газовая постоянная, равная произведения постоянной Авогадро на постоянную Больцмана:

R = N A k = 8 , 31 Д ж / К · м о л ь

Температура — мера кинетической энергии молекул идеального газа:

Полная энергия поступательного движения молекул газа определяется формулой:

Пример №3. При уменьшении абсолютной температуры на 600 К средняя кинетическая энергия теплового движения молекул неона уменьшилась в 4 раза. Какова начальная температура газа?

Запишем формулу, связывающую температуру со средней кинетической энергией теплового движения молекул, для обоих случаев, с учетом что:

Составим систему уравнений:

На графике представлена зависимость объёма постоянного количества молей одноатомного идеального газа от средней кинетической энергии теплового движения молекул газа. Опишите, как изменяются температура и давление газа в процессах 1−2 и 2−3. Укажите, какие закономерности Вы использовали для объяснения.

Алгоритм решения

Решение

График построен в координатах (V;E_k). Процесс 1–2 представляет собой прямую линию, исходящую из начала координат. Это значит, что при увеличении объема растет средняя кинетическая энергия молекул. Но из основного уравнения МКТ идеального газа следует, что мерой кинетической энергии молекул является температура:

Следовательно, когда кинетическая энергия молекул растет, температура тоже растет.

Запишем уравнение Менделеева — Клапейрона:

Так как количество вещества одинаковое для обоих состояния 1 и 2, запишем:

ν R = p 1 V 1 T 1 . . = p 2 V 2 T 2 . .

Мы уже выяснили, что объем и температура увеличиваются пропорционально. Следовательно, давление в состояниях 1 и 2 равны. Поэтому процесс 1–2 является изобарным, давление во время него не меняется.

Процесс 2–3 имеет график в виде прямой линии, перпендикулярной кинетической энергии. Так как температуры прямо пропорциональна кинетической энергии, она остается постоянной вместе с этой энергией. Следовательно, процесс 2–3 является изотермическим, температура во время него не меняется. Мы видим, что объем при этом процессе уменьшается. Но так как объем и давление — обратно пропорциональные величины, то давление на участке 2–3 увеличивается.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Первоначальное давление газа в сосуде равнялось р₁. Увеличив объём сосуда, концентрацию молекул газа уменьшили в 3 раза, и одновременно в 2 раза увеличили среднюю энергию хаотичного движения молекул газа. В результате этого давление р₂ газа в сосуде стало равным

Постоянная Больцмана

Вы будете перенаправлены на Автор24

Как вычислить постоянную Больцмана

Коэффициент $k=1,38cdot ^frac$ — постоянная Больцмана — входит в большое количество формул физики. Назван он в честь австрийского физика Людвига Больцмана, который был одним из создателей молекулярно-кинетической теории. Постоянную Больцмана можно вычислить разными способами, что описаны в Википедии и энциклопедиях по физике. Приведем два из них.

Универсальный метод нахождения постоянной Больцмана

Используем уравнение состояния идеального газа, которое входит искомый коэффициент:

$p=nkT, p=frackT left(1right) $

Из опытов известно, что если нагревать газ (неважно какой) от $T_0$=273 K до $T_1$=373 K его давление изменится от $p_0=1,013cdot ^5Па $ до $p_1=1,38cdot ^5Па$. Опыт простой его можно провести, даже если в качестве газа использовать воздух. Температуру, измеряем термометром, а давление — манометром. При этом мы помним, что один моль любого газа содержит около $6cdot ^$ молекул и при давлении в одну атмосферу занимает объем V=22,4л. Зная вышеназванные параметры состояния системы, проведем расчет постоянной Больцмана. Для этого запишем уравнение (1) дважды, подставляя, параметры состояний:

Используем выше перечисленные данные, найдем значение $k$ по формуле:

Второй метод нахождения постоянной Больцмана

Приведем еще один метод нахождения постоянной Больцмана с помощью маленького зеркала, подвешенного на упругой нити в воздухе. Пусть система воздух — зеркало находится в состоянии статического равновесия. Зеркало подвергается ударам со стороны молекул воздуха и ведет себя, по сути, как броуновская частица, но так как оно подвешено на нити, то мы будем наблюдать крутильные колебания этого зеркала вокруг оси, которая совпадает с вертикальной нитью — подвесом. Поверхность зеркала освещаем лучом света, отраженный луч будет ощутимо смещаться даже при небольших поворотах зеркала. Значит, эти крутильные колебания можно увидеть и измерить. Обозначим модуль кручения нити через$ L$, момент инерции зеркала относительно оси вращения — $J$, поворот зеркала характеризует угол $varphi $. Тогда уравнение крутильных колебаний примет вид:

Готовые работы на аналогичную тему

Минус в (3) означает то, что момент сил упругости направлен таким образом, что стремится вернуть зеркало в положение равновесия. Умножим обе части уравнения (3) на $varphi $ и проведем интегрирование, получим:

Уравнение (4) — закон сохранения энергии для колебаний (кинетическая энергия переходит в потенциальную и наоборот). Малые крутильные колебания можно считать гармоническими, поэтому:

$fracJleftlangle <dot>^2rightrangle =fracLleftlangle ^2rightrangle =frackT left(5right) $

Записывая в уравнении (5) последнюю его часть, мы использовали закон о равномерном распределении энергии по степеням свободы. Из (5) легко получаем:

$leftlangle <dot>^2rightrangle =fracL left(6right)$

Угол поворота, как уже отмечалось, можно измерить. Например, в опыте при $Tapprox 290K, Lapprox ^Нcdot м$ $leftlangle ^2rightrangle approx 4cdot ^$. В таком случае несложно рассчитать значение$ k$:

Из приведенного примера можно сделать вывод о том, что броуновское движение дает возможность вычислить, чему равен коэффициент Больцмана, измеряя макропараметры.

Значение постоянной Больцмана заключается в том, что она позволяет связать параметры, описывающие микромир, с параметрами макромира.

Так, например, она связывает среднюю энергию поступательного движения молекул с термодинамической температурой:

$leftlangle Erightrangle =frackT left(7right) $

МКТ постоянная Больцмана входит в большинство уравнений. Среди них: уравнение состояния идеального газа, средняя энергия молекулы, распределение Максвелла — Больцмана, основное уравнение кинетической теории газов и др. Кроме того, постоянная Больцмана используется в определении энтропии. Она имеет роль в физике полупроводников, к примеру, входит в уравнение, которое устанавливает зависимость электропроводимости от температуры.

Задание:

Газ, состоящий из N-атомных молекул, имеет температуру Т, при которой у молекул возбуждены все степени свободы (поступательные, вращательные и колебательные). Найти среднюю энергию молекулы такого газа. Считать молекулы объемными.

Решение:

Согласно закону равномерного распределения энергии по степеням свободы на каждую степень свободы в среднем приходится одинаковая кинетическая энергия равная $leftlangle _irightrangle =frackT$. В таком случае, можно сказать, что средняя энергия молекулы $leftlangle varepsilon rightrangle $ равна:

$leftlangle varepsilon rightrangle =frackTleft(1.1right) $

где $i=m_+m_+2m_$ — сумма числа поступательных, вращательных и удвоенного количества колебательных степеней свободы, $k$ — постоянная Больцмана, T- термодинамическая температура.

Для успешного решения задачи, в первую очередь определим количество степеней свободы молекулы:

$leftlangle varepsilon rightrangle =frackT=(3N-3)kT$

Ответ: Средняя энергия молекулы такого газа $leftlangle varepsilon rightrangle =(3N-3)kT$.

Задание:

Плотность смеси двух разных идеальных газов при нормальных условиях $rho $. Найти концентрацию атомов одного из газов в данной смеси. Считать, что молярные массы газов ($_1$, $_2$), известны.

Решение:

Общая масса смеси равна:

$m_$ — масса молекулы первого газа, $m_$ — масса молекулы второго газа, $n_1$- концентрация молекул первого газа, $n_2$- концентрация молекул второго газа, $rho $ — плотность смеси.

Выразим концентрацию $n_1 $ из (2.1):

Используем уравнение состояния идеального газа:

Подставим (2.4) в (2.3), получим:

В условии задачи сказано, что известны молярные массы газов ($_1$, $_2$), следовательно, можно найти массы молекул $m_$ и $m_$.

Кроме того, сказано, что газы находятся при нормальных условиях, это значит, что известны давление 1 атм. и температура около 290 К. Таким образом, можно считать, что задача решена.

Ответ: При заданных условиях концентрация одного из газов может быть рассчитана как $n_1=frac<rho -frac

m_><_-m_)>, $где $m_=frac<_1>, m_=frac<_2>.$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 18 12 2021

Постоянная Больцмана

Постоянная Больцмана, представляющая собой коэффициент, равный k = 1 , 38 · 10 — 23 Д ж К , является частью значительного числа формул в физике. Она получила свое название по имени австрийского физика – одного из основоположников молекулярно-кинетической теории. Сформулируем определение постоянной Больцмана:

Постоянной Больцмана называется физическая постоянная, с помощью которой определяется связь между энергией и температурой.

Не следует путать ее с постоянной Стефана-Больцмана, связанной с излучением энергии абсолютно твердого тела.

Существуют различные методы вычисления данного коэффициента. В рамках этой статьи мы рассмотрим два их них.

Нахождение постоянной Больцмана через уравнение идеального газа

Данная постоянная может быть найдена с помощью уравнения, описывающего состояние идеального газа. Опытным путем можно определить, что нагревание любого газа от T 0 = 273 К до T 1 = 373 К приводит к изменению его давления от p 0 = 1 , 013 · 10 5 П а до p 0 = 1 , 38 · 10 5 П а . Это достаточно простой эксперимент, который может быть проведен даже просто с воздухом. Для измерения температуры при этом нужно использовать термометр, а давления – манометр. При этом важно помнить, что количество молекул в моле любого газа примерно равно 6 · 10 23 , а объем при давлении в 1 а т м равен V = 22 , 4 л . С учетом всех названных параметров можно перейти к вычислению постоянной Больцмана k :

Для этого запишем уравнение дважды, подставив в него параметры состояний.

Зная результат, можем найти значение параметра k :

Нахождение постоянной Больцмана через формулу броуновского движения

Для второго способа вычисления нам также потребуется провести эксперимент. Для него нужно взять небольшое зеркало и подвесить в воздухе с помощью упругой нитки. Допустим, что система зеркало-воздух находится в стабильном состоянии (статическом равновесии). Молекулы воздуха ударяют в зеркало, которое, по сути, ведет себя как броуновская частица. Однако с учетом его подвешенного состояния мы можем наблюдать вращательные колебания вокруг определенной оси, совпадающей с подвесом (вертикально направленной нитью). Теперь направим на поверхность зеркала луч света. Даже при незначительных движениях и поворотах зеркала отражающийся в нем луч будет заметно смещаться. Это дает нам возможность измерить вращательные колебания объекта.

Обозначив модуль кручения как L , момент инерции зеркала по отношению к оси вращения как J , а угол поворота зеркала как φ , можем записать уравнение колебаний следующего вида:

Минус в уравнении связан с направлением момента сил упругости, который стремится вернуть зеркало в равновесное положение. Теперь произведем умножение обеих частей на φ , проинтегрируем результат и получим:

Следующее уравнение является законом сохранения энергии, который будет выполняться для данных колебаний (то есть потенциальная энергия будет переходить в кинетическую и обратно). Мы можем считать эти колебания гармоническими, следовательно:

При выведении одной из формул ранее мы использовали закон равномерного распределения энергии по степеням свободы. Значит, можем записать так:

Как мы уже говорили, угол поворота можно измерить. Так, если температура будет равна приблизительно 290 К , а модуль кручения L ≈ 10 — 15 Н · м ; » open=» φ ≈ 4 · 10 — 6 , то рассчитать значение нужного нам коэффициента можно так:

Следовательно, зная основы броуновского движения, мы можем найти постоянную Больцмана с помощью измерения макропараметров.

Значение постоянной Больцмана

Значение изучаемого коэффициента состоит в том, что с его помощью можно связать параметры микромира с теми параметрами, что описывают макромир, например, термодинамическую температуру с энергией поступательного движения молекул:

» open=» E = 3 2 k T .

Этот коэффициент входит в уравнения средней энергии молекулы, состояния идеального газа, кинетической теории газа, распределение Больцмана-Максвелла и многие другие. Также постоянная Больцмана необходима для того, чтобы определить энтропию. Она играет важную роль при изучении полупроводников, например, в уравнении, описывающем зависимость электропроводности от температуры.

Условие: вычислите среднюю энергию молекулы газа, состоящего из N -атомных молекул при температуре T , зная, что у молекул возбуждены все степени свободы – вращательные, поступательные, колебательные. Все молекулы считать объемными.

Энергия равномерно распределяется по степеням свободы на каждую ее степень, значит, на эти степени будет приходиться одинаковая кинетическая энергия. Она будет равна » open=» ε i = 1 2 k T . Тогда для вычисления средней энергии мы можем использовать формулу:

» open=» ε = i 2 k T , где i = m p o s t + m υ r + 2 m k o l представляет собой сумму поступательных вращательных степеней свободы. Буквой k обозначена постоянная Больцмана.

Переходим к определению количества степеней свободы молекулы:

m p o s t = 3 , m υ r = 3 , значит, m k o l = 3 N — 6 .

i = 6 + 6 N — 12 = 6 N — 6 ; » open=» ε = 6 N — 6 2 k T = 3 N — 3 k T .

Ответ: при данных условиях средняя энергия молекулы будет равна » open=» ε = 3 N — 3 k T .

Условие: есть смесь двух идеальных газов, плотность которых в нормальных условиях равна p. Определите, какова будет концентрация одного газа в смеси при условии, что мы знаем молярные массы обоих газов μ 1 , μ 2 .

Сначала вычислим общую массу смеси.

m = ρ V = N 1 m 01 + N 2 m 02 = n 1 V m 01 + n 2 V m 02 → ρ = n 1 m 01 + n 2 m 02 .

Параметр m 01 обозначает массу молекулы одного газа, m 02 – массу молекулы другого, n 2 – концентрацию молекул одного газа, n 2 – концентрацию второго. Плотность смеси равна ρ .

Теперь из данного уравнения выразим концентрацию первого газа:

n 1 = ρ — n 2 m 02 m 01 ; n 2 = n — n 1 → n 1 = ρ — ( n — n 1 ) m 02 m 01 → n 1 = ρ — n m 02 + n 1 m 02 m 01 → n 1 m 01 — n 1 m 02 = ρ — n m 02 → n 1 ( m 01 — m 02 ) = ρ — n m 02 .

Далее нам потребуется уравнение, описывающее состояние идеального газа:

p = n k T → n = p k T .

Подставим полученное равнее значение:

n 1 ( m 01 — m 02 ) = ρ — p k T m 02 → n 1 = ρ — p k T m 02 ( m 01 — m 02 ) .

Поскольку молярные массы газов нам известны, мы можем найти массы молекул первого и второго газа:

m 01 = μ 1 N A , m 02 = μ 2 N A .

Также мы знаем, что смесь газов находится в нормальных условиях, т.е. давление равно 1 а т м , а температура 290 К . Значит, мы можем считать задачу решенной.

Ответ: в данных условиях рассчитать концентрацию одного из газов можно как n 1 = ρ — p k T m 02 ( m 01 — m 02 ) , где m 01 = μ 1 N A , m 02 = μ 2 N A .

📸 Видео