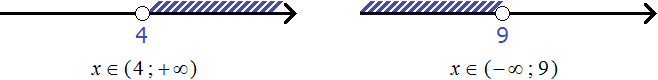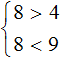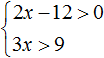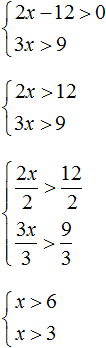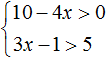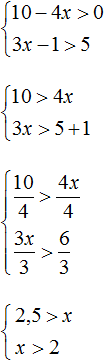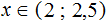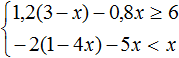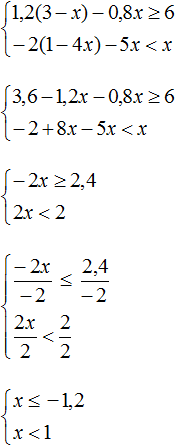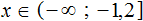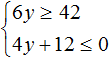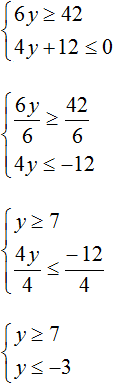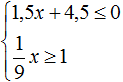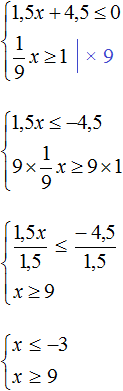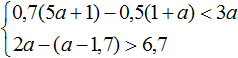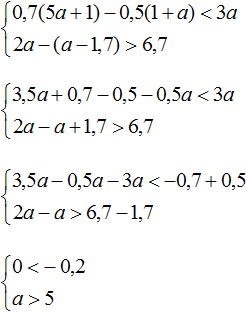Видео:Как решать неравенства? Часть 1| МатематикаСкачать

Примеры решения систем линейных неравенств с одной переменной
Несколько линейных неравенств, удовлетворяющих одним и тем же решениям, образуют систему.
Рассмотрим простейший пример. Система 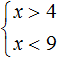
Решениями первого неравенства являются все числа, которые больше 4. Решениями второго неравенства являются все числа, которые меньше 9.
Изобразим множество решений каждого неравенства на координатной прямой и запишем ответы к ним в виде числовых промежутков:
Но дело в том, что неравенства x > 4 и x соединены знаком системы, а значит зависимы друг от друга. Им не дозволяется раскидываться решениями как им захочется. Наша задача указать решения, которые одновременно будут удовлетворять и первому неравенству и второму.
Говоря по-простому, нужно указать числа, которые больше 4, но меньше 9. Очевидно, что речь идет о числах, находящихся в промежутке от 4 до 9.
Значит решениями системы 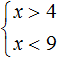
Также, нужно изобразить множество решений системы на координатной прямой.
Для системы линейных неравенств решение на координатной прямой изображают так:
Сначала указывают границы обоих неравенств:
На верхней области отмечают множество решений первого неравенства x > 4
На нижней области отмечают множество решений второго неравенства x (4; 9) , например, число 8
Видим, что решение 8 удовлетворяет обоим неравенствам.
Исходя из рассмотренного примера, можно сформировать правило для решения системы линейных неравенств:
Чтобы решить систему линейных неравенств, нужно по отдельности решить каждое неравенство, и указать в виде числового промежутка множество решений, удовлетворяющих каждому неравенству.
Пример 2. Решить систему неравенств
Решениями первого неравенства являются все числа, которые больше 17. Решениями второго неравенства являются все числа, которые больше 12.
Решениями же обоих неравенств являются все числа, которые больше 17.
Изобразим множество решений системы 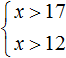
Для начала отметим на координатной прямой границы обоих неравенств:
На верхней области отметим множество решений первого неравенства x > 17
На нижней области отметим множество решений второго неравенства x > 12
Нас интересует область, которая отмечена штрихами с обеих сторон. В этой области и располагаются решения системы 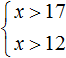
Пример 3. Решить систему неравенств
Решим каждое неравенство по отдельности. Делать это можно внутри системы. Если испытываете затруднения при решении каждого неравенства, обязательно изучите предыдущий урок
Получили систему 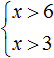
Как и в прошлом примере, сначала нужно отметить границы обоих неравенств, затем отметить множество решений каждого неравенства ( x > 6 и x > 3 ). Область координатной прямой, отмеченная с обеих сторон, будет промежутком, в котором располагается множество решений системы
Пример 4. Решить систему неравенств
Решим каждое неравенство по отдельности:
Изобразим множество решений системы 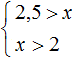
Пример 5. Решить неравенство
Решим каждое неравенство по отдельности:
Изобразим множество решений системы 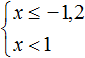
Видео:Система уравнений VS Система неравенств. ОГЭ по математике №9, 13| Математика TutorOnlineСкачать

Когда решений нет
Если неравенства, входящие в систему, не имеют общих решений, то говорят, что система не имеет решений.
Пример 1. Решить неравенство
Решим каждое неравенство по отдельности:
Решениями первого неравенства являются все числа, которые больше 7, включая число 7. Решениями второго неравенства являются все числа, которые меньше −3, включая число −3.
Видим, что у данных неравенств нет общих решений. Увидеть это наглядно позволит координатная прямая. Отметим на ней множество решений каждого неравенства:
На координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Это говорит о том, что неравенства y ≥ 7 и y ≤ −3 не имеют общих решений. Значит не имеет решений система
А если не имеет решений приведённая равносильная система 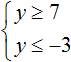
Ответ: решений нет.
Пример 2. Решить систему неравенств
Решим каждое неравенство по отдельности:
Изобразим множество решений неравенств x ≤ −3 и x ≥ 9 на координатной прямой:
Видим, что на координатной прямой нет областей, которые отмечены штрихами с обеих сторон. Значит неравенства x ≤ −3 и x ≥ 9 не имеют общих решений. А значит не имеет решений система
А если не имеет решений приведённая равносильная система 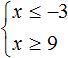
Ответ: решений нет.
Пример 3. Решить систему неравенств
Решим каждое неравенство по отдельности:
Получили неравенства 0 и a > 5 . Первое неравенство не является верным и не имеет решений. Решением второго неравенство a > 5 являются все числа, которые больше 5. Но поскольку первое неравенство не будет верным ни при каком a , то можно сделать вывод, что у неравенств нет общих решений. А значит не имеет решений исходная система
Видео:Решение системы линейных неравенств с одной переменной. 6 класс.Скачать
Алгебра. Урок 8. Неравенства, системы неравенств.
Смотрите бесплатные видео-уроки по теме “Неравенства” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Неравенства
- Линейные неравенства
Видео:Как решать неравенства? Математика 10 класс | TutorOnlineСкачать

Неравенства
Что такое неравенство? Если взять любое уравнение и знак = поменять на любой из знаков неравенства:
≥ больше или равно,
≤ меньше или равно,
то получится неравенство.
Линейные неравенства
Линейные неравенства – это неравенства вида:
a x b a x ≤ b a x > b a x ≥ b
где a и b – любые числа, причем a ≠ 0, x – переменная.
Примеры линейных неравенств:
3 x 5 x − 2 ≥ 0 7 − 5 x 1 x ≤ 0
Решить линейное неравенство – получить выражение вида:
x c x ≤ c x > c x ≥ c
где c – некоторое число.
Последний шаг в решении неравенства – запись ответа. Давайте разбираться, как правильно записывать ответ.
- Если знак неравенства строгий > , , точка на оси будет выколотой (не закрашенной), а скобка, обнимающая точку – круглой .
Смысл выколотой точки в том, что сама точка в ответ не входит.
- Если знак неравенства нестрогий ≥ , ≤ , точка на оси будет жирной (закрашенной), а скобка, обнимающая точку – квадратной .
Смысл жирной точки в том, что сама точка входит в ответ.
- Скобка, которая обнимает знак бесконечности всегда круглая – не можем мы объять необъятное, как бы нам этого ни хотелось.
Таблица числовых промежутков
| Неравенство | Графическое решение | Форма записи ответа |
|---|---|---|
| x c | x ∈ ( − ∞ ; c ) | |
| x ≤ c | x ∈ ( − ∞ ; c ] | |
| x > c | x ∈ ( c ; + ∞ ) | |
| x ≥ c | Алгоритм решения линейного неравенства
a x b a x ≤ b a x > b a x ≥ b
Примеры решения линейных неравенств: №1. Решить неравенство 3 ( 2 − x ) > 18. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. − 3 x > 18 − 6 − 3 x > 12 | ÷ ( − 3 ) Делим обе части неравенства на ( -3 ) – коэффициент, который стоит перед x . Так как − 3 0 , знак неравенства поменяется на противоположный . x 12 − 3 ⇒ x − 4 Остается записать ответ (см. таблицу числовых промежутков). Ответ: x ∈ ( − ∞ ; − 4 ) №2. Решить неравество 6 x + 4 ≥ 3 ( x + 1 ) − 14. Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x + 4 ≥ 3 x + 3 − 14 6 x − 3 x ≥ 3 − 14 − 4 3 x ≥ − 15 | ÷ 3 Делим обе части неравенства на ( 3 ) – коэффициент, который стоит перед x . Так как 3 > 0, знак неравенства после деления меняться не будет. x ≥ − 15 3 ⇒ x ≥ − 5 Остается записать ответ (см. таблицу числовых промежутков). Особые случаи (в 14 задании ОГЭ 2019 они не встречались, но знать их полезно). №1. Решить неравенство 6 x − 1 ≤ 2 ( 3 x − 0,5 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. 6 x − 6 x ≤ − 1 + 1 Получили верное неравенство, которое не зависит от переменной x . Возникает вопрос, какие значения может принимать переменная x , чтобы неравенство выполнялось? Любые! Какое бы значение мы ни взяли, оно все равно сократится и результат неравенства будет верным. Рассмотрим три варианта записи ответа. Ответ:
№2. Решить неравенство x + 3 ( 2 − 3 x ) > − 4 ( 2 x − 12 ). Решение: Раскрываем скобки, переносим иксы влево, числа вправо, приводим подобные слагаемые. x + 6 − 9 x > − 8 x + 48 − 8 x + 8 x > 48 − 6 Получили неверное равенство, которое не зависит от переменной x . Какие бы значения мы ни подставляли в исходное неравенство, результат окажется одним и тем же – неверное неравенство. Ни при каких значениях x исходное неравенство не станет верным. Данное неравенство не имеет решений. Запишем ответ. Квадратные неравенства Квадратные неравенства – это неравенства вида: a x 2 + b x + c > 0 a x 2 + b x + c ≥ 0 a x 2 + b x + c 0 a x 2 + b x + c ≤ 0 где a, b, c — некоторые числа, причем a ≠ 0, x — переменная. Существует универсальный метод решения неравенств степени выше первой (квадратных, кубических, биквадратных и т.д.) – метод интервалов. Если его один раз как следует осмыслить, то проблем с решением любых неравенств не возникнет. Для того, чтобы применять метод интервалов для решения квадратных неравенств, надо уметь хорошо решать квадратные уравнения (см. урок 4). Алгоритм решения квадратного неравенства методом интервалов
Если знак неравенства строгий > , , точки будут выколотые. Если знак неравенства нестрогий ≥ , ≤ , точки будут жирные (заштрихованный).
Если получилось положительное число, знак на интервале плюс. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий. Если получилось отрицательное число, знак на интервале минус. На остальных интервалах знаки будут чередоваться. Точки выколотые, если знак неравенства строгий. Точки жирные, если знак неравенства нестрогий.
Если знак неравенства > или ≥ в ответ выбираем интервалы со знаком +. Если знак неравенства или ≤ в ответ выбираем интервалы со знаком -. Примеры решения квадратных неравенств: №1. Решить неравенство x 2 ≥ x + 12. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 1, c = − 12 D = b 2 − 4 a c = ( − 1 ) 2 − 4 ⋅ 1 ⋅ ( − 12 ) = 1 + 48 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 1 ) ± 49 2 ⋅ 1 = 1 ± 7 2 = [ 1 + 7 2 = 8 2 = 4 1 − 7 2 = − 6 2 = − 3 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 6 . Подставляем эту точку в исходное выражение: x 2 − x − 1 = 6 2 − 6 − 1 = 29 > 0 Это значит, что знак на интервале, в котором лежит точка 6 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. В ответ пойдут два интервала. В математике для объединения нескольких интервалов используется знак объединения: ∪ . Точки -3 и 4 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 3 ] ∪ [ 4 ; + ∞ ) №2. Решить неравенство − 3 x − 2 ≥ x 2 . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = − 2 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ ( − 2 ) = 9 − 8 = 1 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 1 2 ⋅ ( − 1 ) = 3 ± 1 − 2 = [ 3 + 1 − 2 = 4 − 2 = − 2 3 − 1 − 2 = 2 − 2 = − 1 x 1 = − 2, x 2 = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение: − x 2 − 3 x − 2 = − ( 0 ) 2 − 3 ⋅ 0 − 2 = − 2 0 Это значит, что знак на интервале, в котором лежит точка 0 будет − . Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервал со знаком +. Точки -2 и -1 будут в квадратных скобках, так как они жирные. Ответ: x ∈ [ − 2 ; − 1 ] №3. Решить неравенство 4 x 2 + 3 x . Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = − 1, b = − 3, c = 4 D = b 2 − 4 a c = ( − 3 ) 2 − 4 ⋅ ( − 1 ) ⋅ 4 = 9 + 16 = 25 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 3 ) ± 25 2 ⋅ ( − 1 ) = 3 ± 5 − 2 = [ 3 + 5 − 2 = 8 − 2 = − 4 3 − 5 − 2 = − 2 − 2 = 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение: − x 2 − 3 x + 4 = − ( 2 ) 2 − 3 ⋅ 2 + 4 = − 6 0 Это значит, что знак на интервале, в котором лежит точка 2 , будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервалы со знаком − . Точки -4 и 1 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − ∞ ; − 4 ) ∪ ( 1 ; + ∞ ) №4. Решить неравенство x 2 − 5 x 6. Решение: Приводим неравенство к виду a x 2 + b x + c ≥ 0, а затем решаем уравнение a x 2 + b x + c = 0. a = 1, b = − 5, c = − 6 D = b 2 − 4 a c = ( − 5 ) 2 − 4 ⋅ 1 ⋅ ( − 6 ) = 25 + 25 = 49 D > 0 ⇒ будет два различных действительных корня x 1,2 = − b ± D 2 a = − ( − 5 ) ± 49 2 ⋅ 1 = 5 ± 7 2 = [ 5 + 7 2 = 12 2 = 6 5 − 7 2 = − 2 2 = − 1 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 10. Подставляем эту точку в исходное выражение: x 2 − 5 x − 6 = 10 2 − 5 ⋅ 10 − 6 = 100 − 50 − 6 = 44 > 0 Это значит, что знак на интервале, в котором лежит точка 10 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком -. Точки -1 и 6 будут в круглых скобках, так как они выколотые Ответ: x ∈ ( − 1 ; 6 ) №5. Решить неравенство x 2 4. Решение: Переносим 4 в левую часть, раскладываем выражение на множители по ФСУ и находим корни уравнения. ( x − 2 ) ( x + 2 ) = 0 ⇔ [ x − 2 = 0 x + 2 = 0 [ x = 2 x = − 2 Наносим точки на ось x . Так как знак неравенства строгий, точки будут выколотыми. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 3 . Подставляем эту точку в исходное выражение: x 2 − 4 = 3 2 − 4 = 9 − 4 = 5 > 0 Это значит, что знак на интервале, в котором лежит точка 3 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства , выбираем в ответ интервал со знаком − . Точки -2 и 2 будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 2 ; 2 ) №6. Решить неравенство x 2 + x ≥ 0. Решение: Выносим общий множитель за скобку, находим корни уравнения x 2 + x = 0. x ( x + 1 ) = 0 ⇔ [ x = 0 x + 1 = 0 [ x = 0 x = − 1 Наносим точки на ось x . Так как знак неравенства нестрогий, точки будут жирными. Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 1 . Подставляем эту точку в исходное выражение: x 2 + x = 1 2 + 1 = 2 > 0 Это значит, что знак на интервале, в котором лежит точка 1 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный. Поскольку знак неравенства ≥ , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -1 и 0 будут в квадратных скобках, так как они жирные. Ответ: x ∈ ( − ∞ ; − 1 ] ∪ [ 0 ; + ∞ ) Вот мы и познакомились с методом интервалов. Он нам еще пригодится при решении дробно рациональных неравенств, речь о которых пойдёт ниже. Дробно рациональные неравенства Дробно рациональное неравенство – это неравенство, в котором есть дробь, в знаменателе которой стоит переменная, т.е. неравенство одного из следующих видов: f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0 Дробно рациональное неравенство не обязательно сразу выглядит так. Иногда, для приведения его к такому виду, приходится потрудиться (перенести слагаемые в левую часть, привести к общему знаменателю). Примеры дробно рациональных неравенств: x − 1 x + 3 0 3 ( x + 8 ) ≤ 5 x 2 − 1 x > 0 x + 20 x ≥ x + 3 Как же решать эти дробно рациональные неравенства? Да всё при помощи того же всемогущего метода интервалов. Алгоритм решения дробно рациональных неравенств:
f ( x ) g ( x ) 0 f ( x ) g ( x ) ≤ 0 f ( x ) g ( x ) > 0 f ( x ) g ( x ) ≥ 0
В этом пункте алгоритма мы будем делать всё то, что нам запрещали делать все 9 лет обучения в школе – приравнивать знаменатель дроби к нулю. Чтобы как-то оправдать свои буйные действия, полученные точки при нанесении на ось x будем всегда рисовать выколотыми, вне зависимости от того, какой знак неравенства.
Вне зависимости от знака неравенства Если знак неравенства строгий , Если знак неравенства нестрогий ,
Примеры решения дробно рациональных неравенств: №1. Решить неравенство x − 1 x + 3 > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
x = 1 — это ноль числителя . Поскольку знак неравенства строгий, ноль числителя при нанесени на ось x будет выколотым. Запомним это.
x = − 3 — это ноль знаменателя . При нанесении на ось x точка будет всегда выколотой (вне зависимости от знака неравенства) .
При нанесении нулей числителя обращаем внимание на знак неравенства. В данном случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x − 1 x + 3 = 2 − 1 2 + 3 = 1 5 > 0, Это значит, что знак на интервале, в котором лежит точка 2 будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Точки -3 и 1 будут в круглых скобках, так как обе они выколотые. Ответ: x ∈ ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ ) №2. Решить неравенство 3 ( x + 8 ) ≤ 5. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
3 ( x + 8 ) − 5 x + 8 ≤ 0 3 x + 8 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 ( x + 8 ) x + 8 ≤ 0 3 − 5 x − 40 x + 8 ≤ 0 − 5 x − 37 x + 8 ≤ 0
x = − 37 5 = − 37 5 = − 7,4 x = − 7,4 — ноль числителя . Поскольку знак неравенства нестрогий, при нанесении этой точки на ось x точка будет жирной.
x = − 8 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства нестрогий, значит нули числителя будут жирными. Ну а нули знаменателя выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 0 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : − 5 x − 37 x + 8 = − 5 ⋅ 0 − 37 0 + 8 = − 37 8 0 Это значит, что знак на интервале, в котором лежит точка 0 будет -. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства ≤ , выбираем в ответ интервалы со знаком -. В ответ пойдут два интервала. Точка -8 будет в круглой скобке, так как она выколотая, точка -7,4 будет в квадратных скобках, так как она жирная. Ответ: x ∈ ( − ∞ ; − 8 ) ∪ [ − 7,4 ; + ∞ ) №3. Решить неравенство x 2 − 1 x > 0. Решение: Будем решать данное неравенство в соответствии с алгоритмом.
( x − 1 ) ( x + 1 ) = 0 ⇒ [ x − 1 = 0 x + 1 = 0 [ x = 1 x = − 1 x 1 = 1, x 2 = − 1 — нули числителя . Поскольку знак неравенства строгий, при нанесении этих точек на ось x точки будут выколотыми.
x = 0 — это ноль знаменателя . При нанесении на ось x , точка будет всегда выколотой (вне зависимости от знака неравенства).
При нанесении нулей числителя обращаем внимание на знак неравенства. В данному случае знак неравенства строгий, значит нули числителя будут выколотыми. Ну а нули знаменателя и так выколоты всегда.
Выбираем точку из любого интервала для проверки знака на интервале. Пусть это будет точка 2 . Подставляем эту точку в исходное выражение f ( x ) g ( x ) : x 2 − 1 x = 2 2 − 1 2 = 4 − 1 2 = 3 2 > 0, Это значит, что знак на интервале, в котором лежит точка 2, будет +. Далее расставляем знаки справа налево. При переходе через найденные нулевые точки знак будет меняться на противоположный.
Поскольку знак неравенства > , выбираем в ответ интервалы со знаком +. В ответ пойдут два интервала. Все точки будут в круглых скобках, так как они выколотые. Ответ: x ∈ ( − 1 ; 0 ) ∪ ( 1 ; + ∞ ) Системы неравенств Системой неравенств называют два неравенства с одной неизвестной, которые объединены в общую систему фигурной скобкой. Пример системы неравенств: Алгоритм решения системы неравенств
Примеры решений систем неравенств: №1. Решить систему неравенств < 2 x − 3 ≤ 5 7 − 3 x ≤ 1 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
2 x ≤ 8 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 4 на графике жирная, так как знак неравенства нестрогий.
− 3 x ≤ − 6 | ÷ ( − 3 ), поскольку − 3 0, знак неравенства после деления меняется на противоположный. Графическая интерпретация решения: Точка 2 на графике жирная, так как знак неравенства нестрогий.
Пересечение решений наблюдается на отрезке от 2 до 4 . Точки 2 и 4 в ответе буду в квадратных скобках, так как обе они жирные. №2. Решить систему неравенств < 2 x − 1 ≤ 5 1 − 3 x − 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
2 x ≤ 6 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Точка 3 на графике жирная, так как знак неравенства нестрогий.
3 x − 3 | ÷ 3 , поскольку 3 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения: Точка -1 на графике выколотая, так как знак неравенства строгий.
Пересечение решений наблюдается на самом левом участке. Точка -1 будет в ответе в круглых скобках, так как она выколотая. Ответ: x ∈ ( − ∞ ; − 1 ) №3. Решить систему неравенств 5 − x Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения:
2 x > 12 | ÷ 2 , поскольку 2 > 0, знак неравенства после деления сохраняется. Графическая интерпретация решения:
Пересечений решений не наблюдается. Значит у данной системы неравенств нет решений. №4. Решить систему неравенств 0 2 x + 3 ≤ x 2 Решение: Будем решать данную систему неравенств в соответствии с алгоритмом.
Графическая интерпретация решения первого неравенства:
Решаем методом интервалов. a = − 1, b = 2, c = 3 D = b 2 − 4 a c = 2 2 − 4 ⋅ ( − 1 ) ⋅ 3 = 4 + 12 = 16 D > 0 — два различных действительных корня. x 1,2 = − b ± D 2 a = − 2 ± 16 2 ⋅ ( − 1 ) = − 2 ± 4 − 2 = [ − 2 − 4 − 2 = − 6 − 2 = 3 − 2 + 4 − 2 = 2 − 2 = − 1 Наносим точки на ось x и расставляем знаки на интервалах. Поскольку знак неравенства нестрогий, обе точки будут заштрихованными. Графическая интерпретация решения второго неравенства:
Пересечение решений наблюдается в двух интервалах. Для того, чтобы в ответе объединить два интервала, используется знак объединения ∪ . Точка -4 будет в круглой скобке, так как она выколотая, а точки -1 и 3 в квадратных, так как они жирные. Видео:Решение квадратных неравенств | МатематикаСкачать  Системы неравенств: определение, виды, примеры решенияСтатья раскрывает тему неравенств, разбираются определения систем и их решения. Будут рассмотрены часто встречающиеся примеры решения систем уравнений в школе на алгебре. Видео:Как решать уравнения и неравенства? | Ботай со мной #072 | Борис Трушин |Скачать  Определение системы неравенствСистемы неравенств определяют по определениям систем уравнений, значит, что особое внимание уделяется записям и смыслу самого уравнения. Системой неравенств называют запись уравнений, объединенных фигурной скобкой с множеством решений одновременно для всех неравенств, входящих в систему. Ниже приведены примеры неравенств. Даны два неравенства 2 · x − 3 > 0 и 5 − x ≥ 4 · x − 11 . Необходимо записать одно уравнение под другим, после чего объединим при помощи фигурной скобки: 2 · x — 3 > 0 , 5 — x ≥ 4 · x — 11 Таким же образом определение систем неравенств представлены в школьных учебниках как для использования одной переменной, так и двух. Видео:ЛИНЕЙНЫЕ НЕРАВЕНСТВА - Как решать линейные неравенства // Подготовка к ЕГЭ по МатематикеСкачать  Основные виды системы неравенствИмеет место составление бесконечного множества систем неравенств. Их классифицируют по группам, отличающихся по определенным признакам. Неравенства подразделяют по критериям:
Количество входящих неравенств может насчитывать от двух и более. В предыдущем пункте рассматривался пример решения системы с двумя неравенствами. 2 · x — 3 > 0 , 5 — x ≥ 4 · x — 11 Рассмотрим решение системы с четырьмя неравенствами. x ≥ — 2 , y ≤ 5 , x + y + z ≥ 3 , z ≤ 1 — x 2 — 4 · y 2 Решение неравенства отдельно не говорит о решение системы в целом. Для решения системы необходимо задействовать все имеющиеся неравенства. Такие системы неравенств могут иметь одну, две, три и более переменных. В последней изображенной системе это отчетливо видно, там имеем три переменные: x , y , z . Уравнения могут содержать по одной переменной, как в примере, либо по несколько. Исходя из примеров, неравенство x + 0 · y + 0 · z ≥ − 2 и 0 · x + y + 0 · z ≤ 5 не считают равнозначными. Школьным программам уделяют внимание решению неравенств с одной переменной. При записи системы могут быть задействованы уравнения разных видов и с разным количеством переменных. Чаще всего встречаются целые неравенства разных степеней. При подготовке к экзаменам могут встретиться системы с иррациональными, логарифмическими, показательными уравнениями вида: 544 — 4 — x 32 — 2 — x ≥ 17 , log x 2 16 x + 20 16 ≤ 1 Такая система включает в себя показательное и логарифмическое уравнение. Видео:Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства | TutorOnlineСкачать  Решение системы неравенствРешение системы неравенств с одной переменной – это значение переменной, которое обращает каждое неравенство заданной системы в верное числовое неравенство, то есть будет являться решением каждого имеющегося неравенства. Рассмотрим пример решения систем уравнений с одной переменной. x > 7 , 2 — 3 · x ≤ 0 Если значение х = 8 , то решение системы очевидно, так как выполняется 8 > 7 и 2 − 3 · 8 ≤ 0 . При х = 1 система не решится, так как первое числовое неравенство во время подстановки имеет 1 > 7 . Таким же образом решается система с двумя и более переменными. Решение системы неравенств с двумя и более переменными называют значения, которые являются решением всех неравенств при обращении каждого в верное числовое неравенство. Если х = 1 и у = 2 будет решением неравенства x + y 7 x — y 0 , потому как выражения 1 + 2 7 и 1 − 2 0 верны. Если подставить числовую пару ( 3 , 5 , 3 ) , тогда система не даст значения переменных и неравенство будет неверным 3 , 5 − 3 0 . При решении системы неравенств могут давать определенное количество ответов, а могут и бесконечное. Имеется ввиду множество решений такой системы. При отсутствии решений говорят о том, что она имеет пустое множество решений. Если решение имеет определенное число, тогда множества решений имеет конечное число элементов. Если решений много, тогда множество решений содержит бесконечное множество чисел. Некоторые учебники дают определение частного решения системы неравенств, которое понимается как отдельно взятое решение. А общим решением системы неравенств считают все его частные решения. Такое определение используется редко, поэтому говорят «решение системы неравенств». Данные определения систем неравенств и решения рассматриваются как пересечения множеств решений всех неравенств системы. Особое внимание стоит уделить разделу, посвященному равносильным неравенствам. 🎦 ВидеоПодготовка к ОГЭ . Рациональные неравенства | Математика | TutorOnlineСкачать  Линейное неравенство с одной переменной. 6 класс.Скачать  Решение системы неравенствСкачать  Линейное неравенство с одной переменной. 6 класс.Скачать  Неравенства с двумя переменными. 9 класс.Скачать  Решение неравенства методом интерваловСкачать  ПРОСТЕЙШИЙ метод решения систем квадратных неравенствСкачать  Неравенства с модулем | Математика | TutorOnlineСкачать  Как решать уравнения с модулем или Математический торт с кремом (часть 1) | МатематикаСкачать  Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать  КВАДРАТНЫЕ НЕРАВЕНСТВА ПОНЯТНЫМ ЯЗЫКОМСкачать  Линейное уравнение с одной переменной. 6 класс.Скачать  |