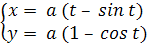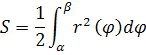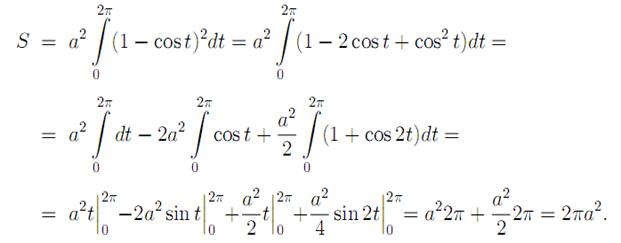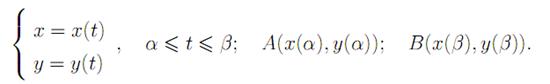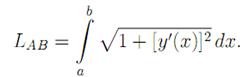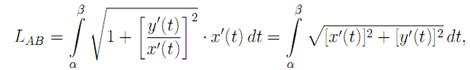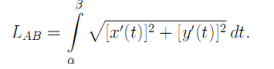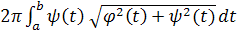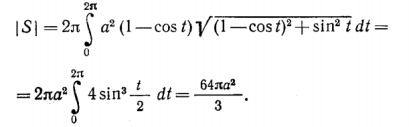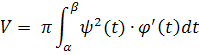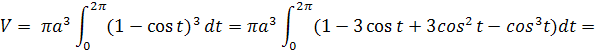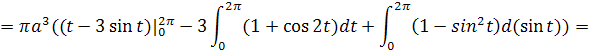Уравнение и график циклоиды в (6 видео)

Уравнения кривых. Циклоида.

Циклоида (от греческого — круглый). – кривая которую формирует фиксированная точка окружности радиуса r, катящейся без скольжения по неподвижной прямой. Термин «циклоида» предложил Г. Галилей.

Точки, в которых циклоида пересекается с прямой, по которой катится окружность (эту окружность обозначают как производящую, а прямую, по которой она катится, – направляющую), обозначают как точки возврата, а самые высокие точки на циклоиде, размещенные посредине между соседними точками возврата, именуют вершинами циклоиды,

Обозначим горизонтальную ось координат как прямую, по которой катится формирующая окружность радиуса r. Тогда имеем нижеследующие уравнения в прямоугольной системе координат:

Циклоида характеризуется параметрическими уравнениями:

Циклоиду можно получить в результате решения дифференциального уравнения:

Содержание

Циклоида ⁠
совместно с Еленой Зёрнышкиной
Параметрическое уравнение циклоиды и уравнение в декартовых координатах
🌟 Видео

Видео:построение циклоидыСкачать

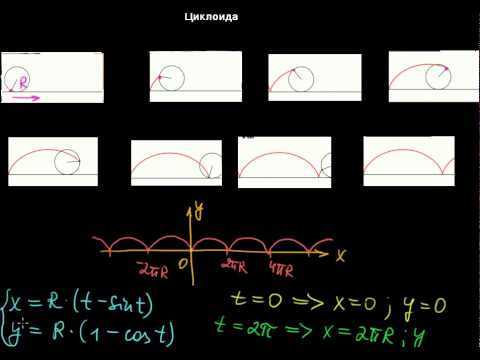
Циклоида ⁠

Видео:10 класс, 43 урок, Уравнение касательной к графику функцииСкачать

совместно с Еленой Зёрнышкиной

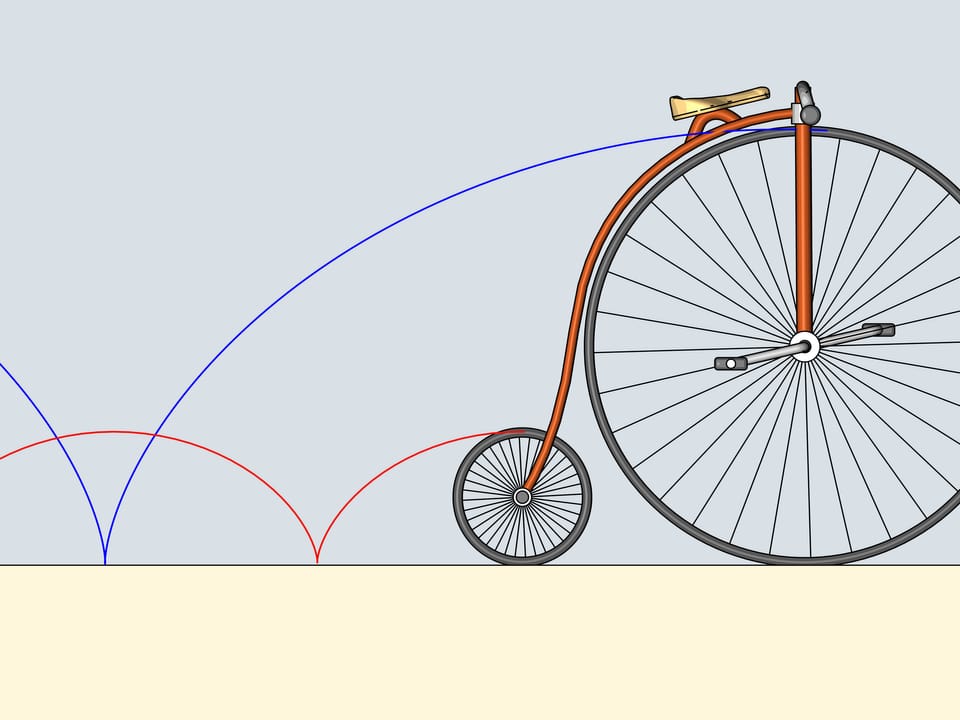
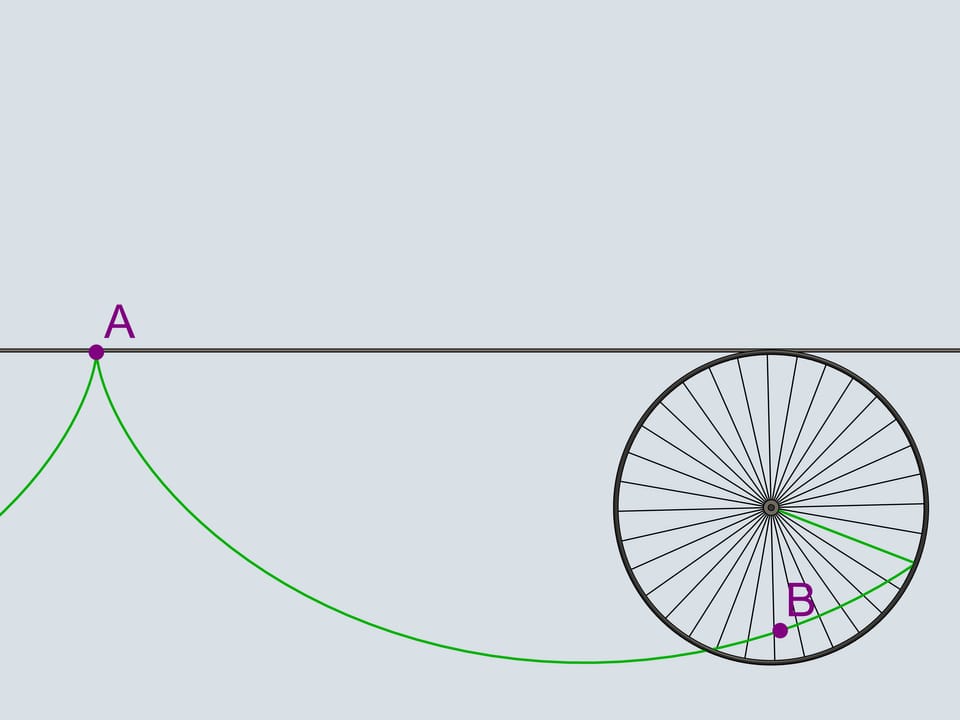
Помните оранжевые пластмассовые катафоты — светоотражатели, прикрепляющиеся к спицам велосипедного колеса? Прикрепим катафот к самому ободу колеса и проследим за его траекторией. Полученные кривые принадлежат семейству циклоид.

Колесо при этом называется производящим кругом (или окружностью) циклоиды.

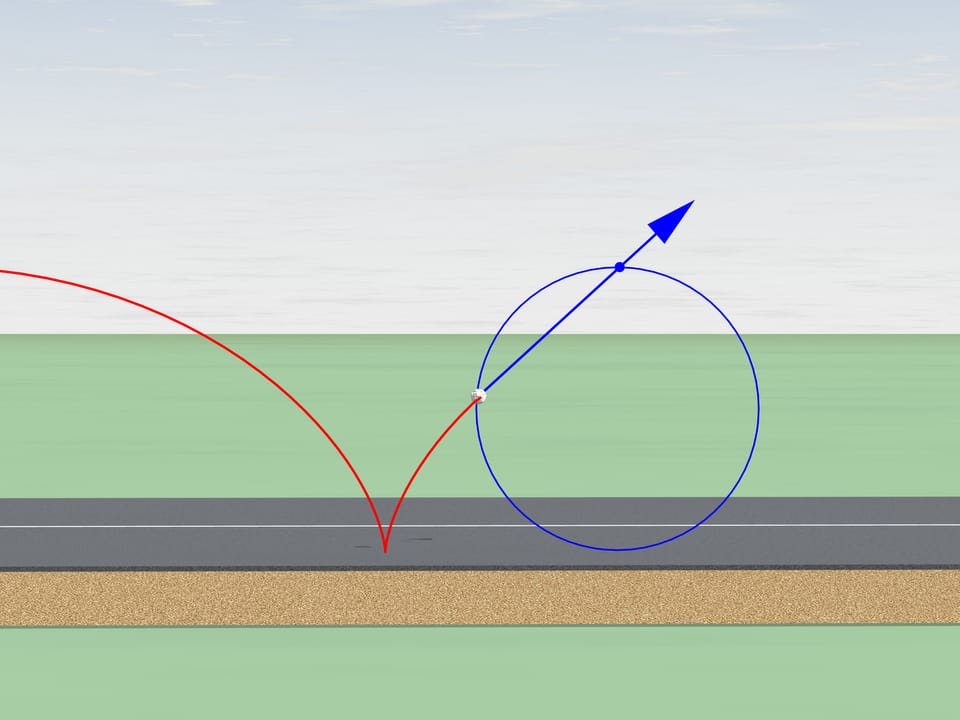
Но давайте вернёмся в наш век и пересядем на более современную технику. На пути байка попался камушек, который застрял в протекторе колеса. Провернувшись несколько кругов с колесом, куда полетит камень, когда выскочит из протектора? Против направления движения мотоцикла или по направлению?

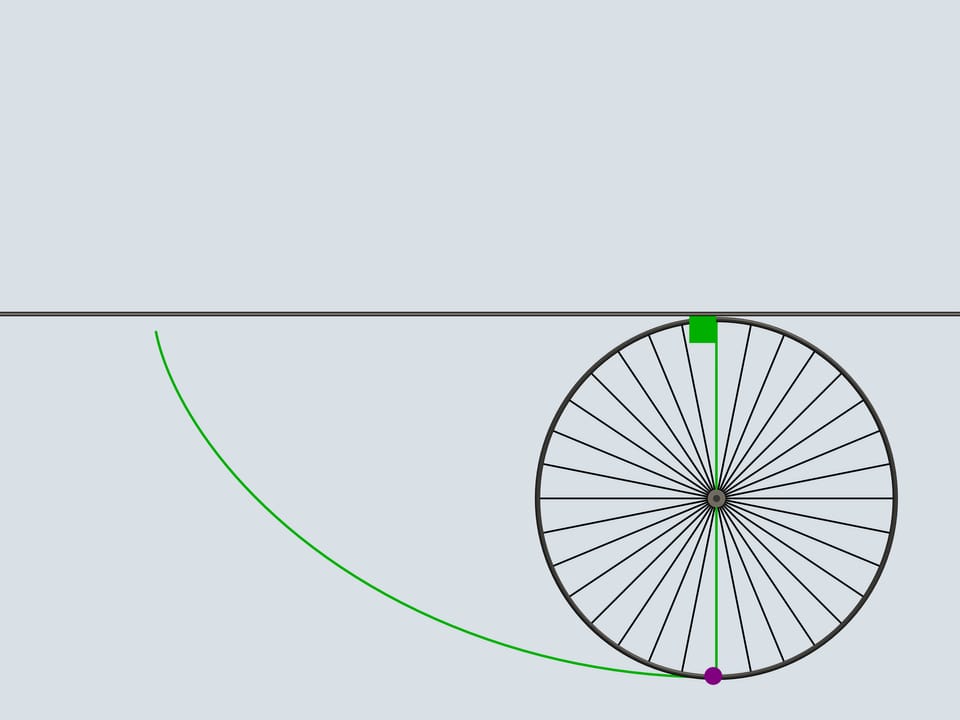
Как известно, свободное движение тела начинается по касательной к той траектории, по которой оно двигалось. Касательная к циклоиде всегда направлена по направлению движения и проходит через верхнюю точку производящей окружности. По направлению движения полетит и наш камушек.

Помните, как Вы катались в детстве по лужам на велосипеде без заднего крыла? Мокрая полоска на вашей спине является житейским подтверждением только что полученного результата.

Век XVII — это век циклоиды. Лучшие учёные изучали её удивительные свойства.

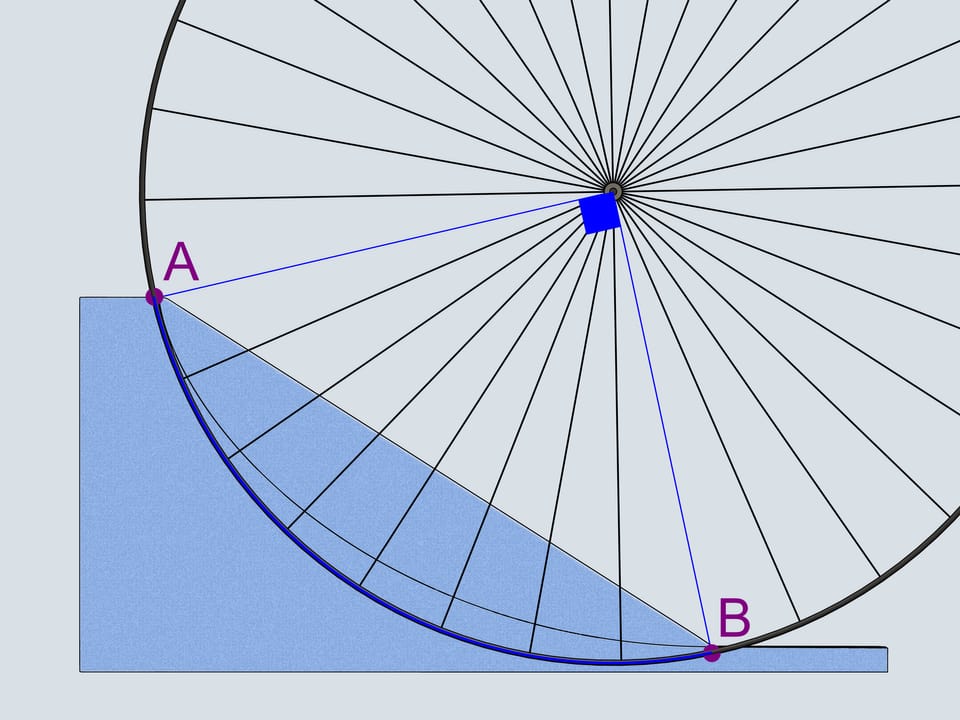
Какая траектория приведёт тело, движущееся под действием силы тяжести, из одной точки в другую за кратчайшее время? Это была одна из первых задач той науки, которая сейчас носит название вариационное исчисление.

Минимизировать (или максимизировать) можно разные вещи — длину пути, скорость, время. В задаче о брахистохроне минимизируется именно время (что подчёркивается самим названием: греч. βράχιστος — наименьший, χρόνος — время).

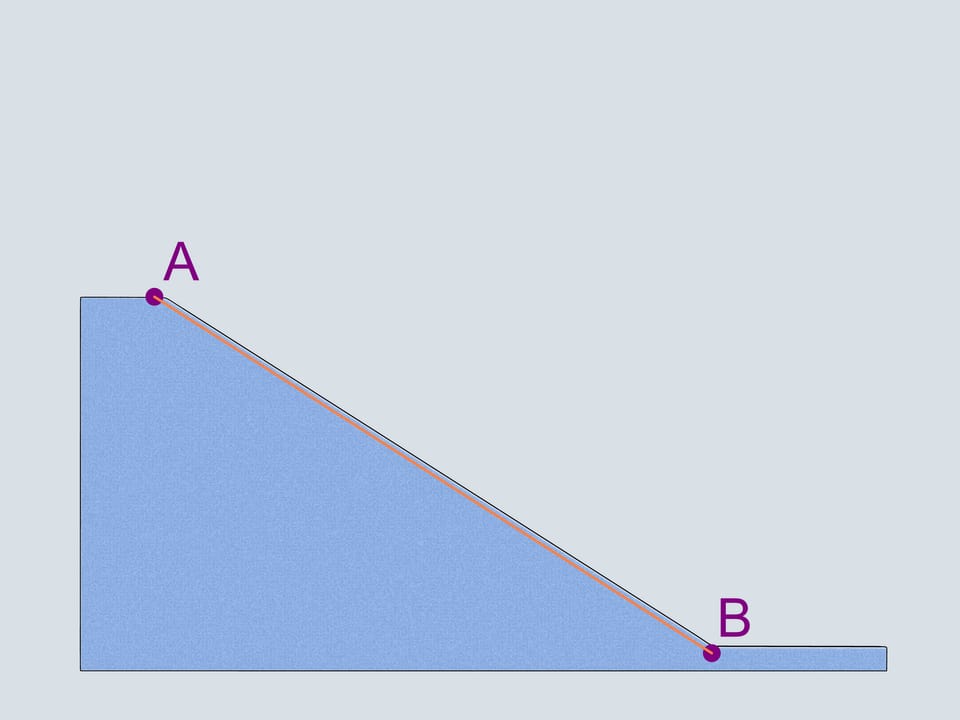
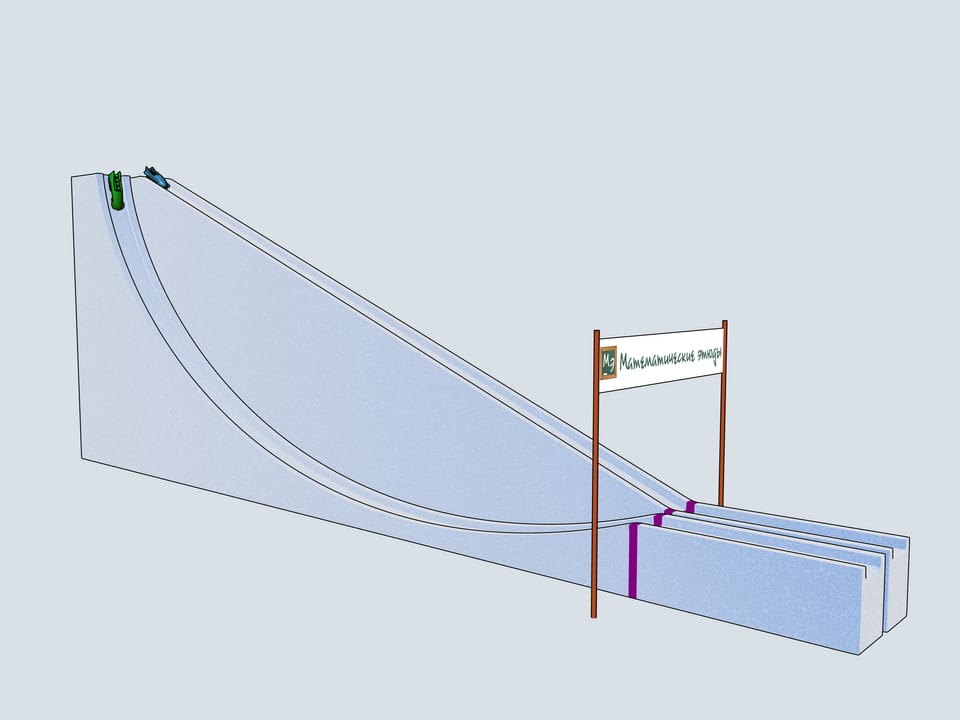
Первое, что приходит на ум, — это прямолинейная траектория. Давайте также рассмотрим перевёрнутую циклоиду с точкой возврата в верхней из заданных точек. И, следуя за Галилео Галилеем, — четвертинку окружности, соединяющую наши точки.

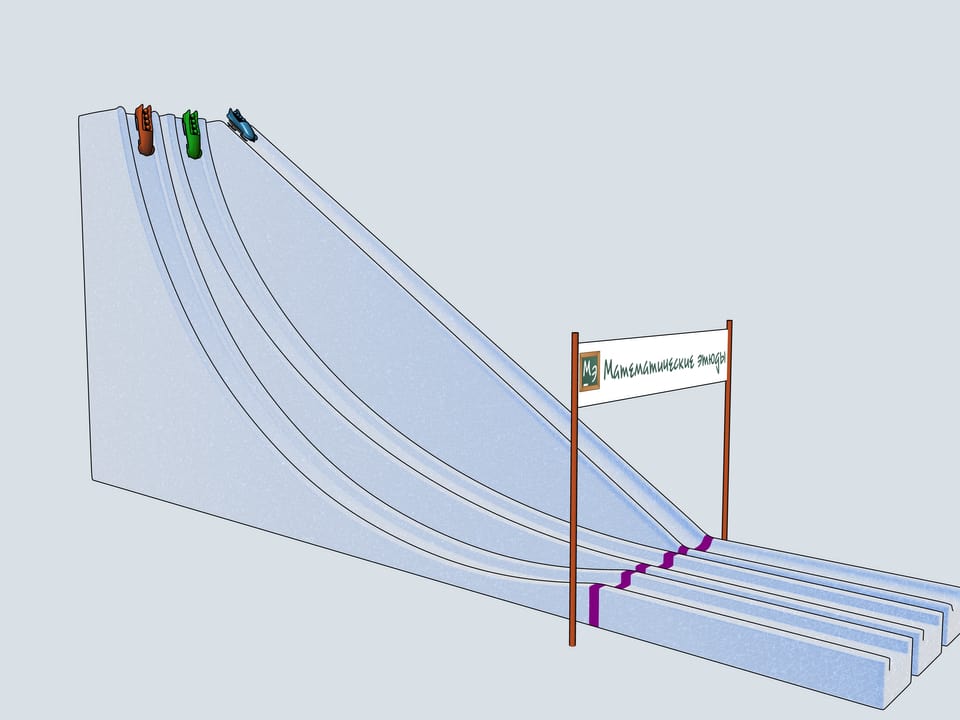
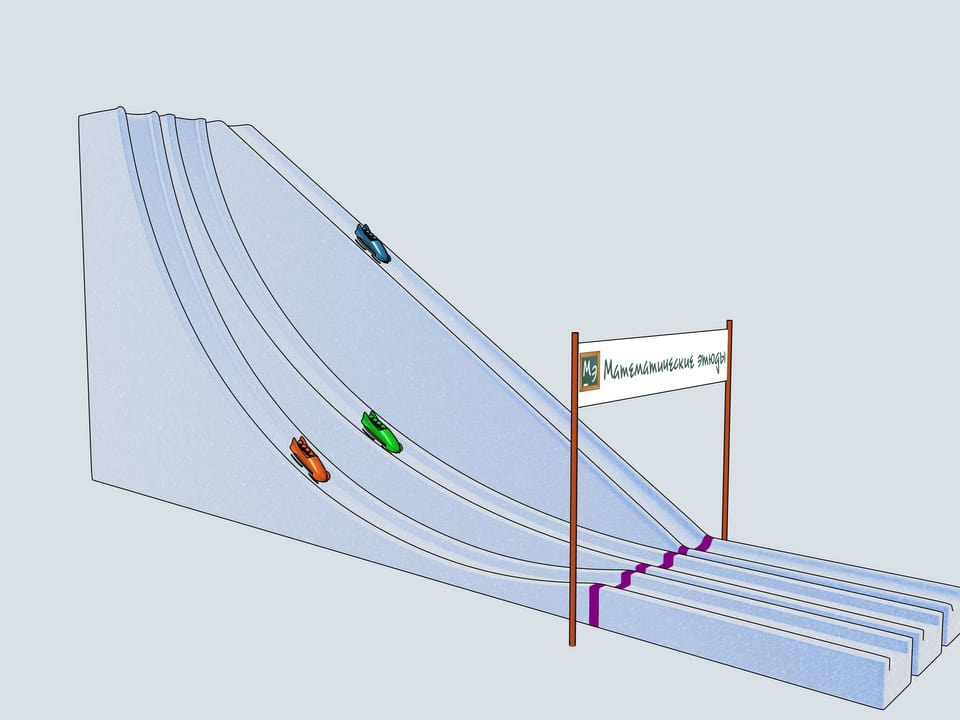
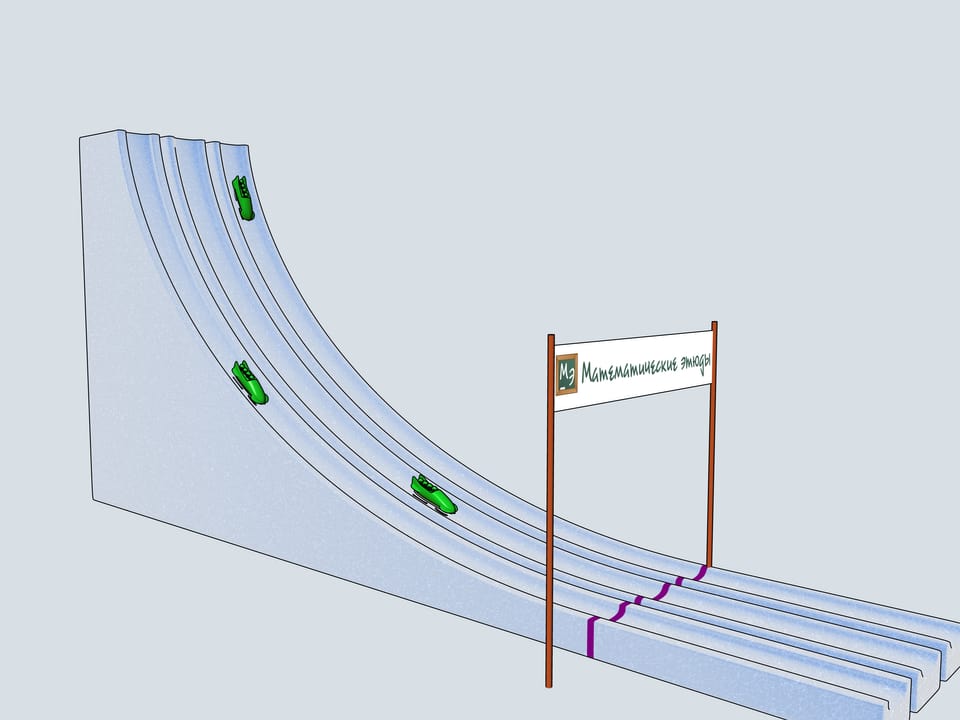
Сделаем бобслейные трассы с рассмотренными профилями и проследим, какой из бобов приедет первым.

История бобслея берёт своё начало в Швейцарии. В 1924 году во французском городе Шамони проходят первые зимние Олимпийские игры. На них уже проводятся соревнования по бобслею для экипажей двоек и четвёрок. Единственный год, когда на Олимпийских играх экипаж боба состоял из пяти человек, был 1928. С тех пор в бобслее всегда соревнуются мужские экипажи двойки и четвёрки. В правилах бобслея много интересного. Конечно же, существует ограничения на вес боба и команды, но существуют даже ограничения на материалы, которые можно использовать в коньках боба (передняя пара их подвижна и связана с рулём, задняя закреплена жёстко). Например, радий не может использоваться при изготовлении коньков.

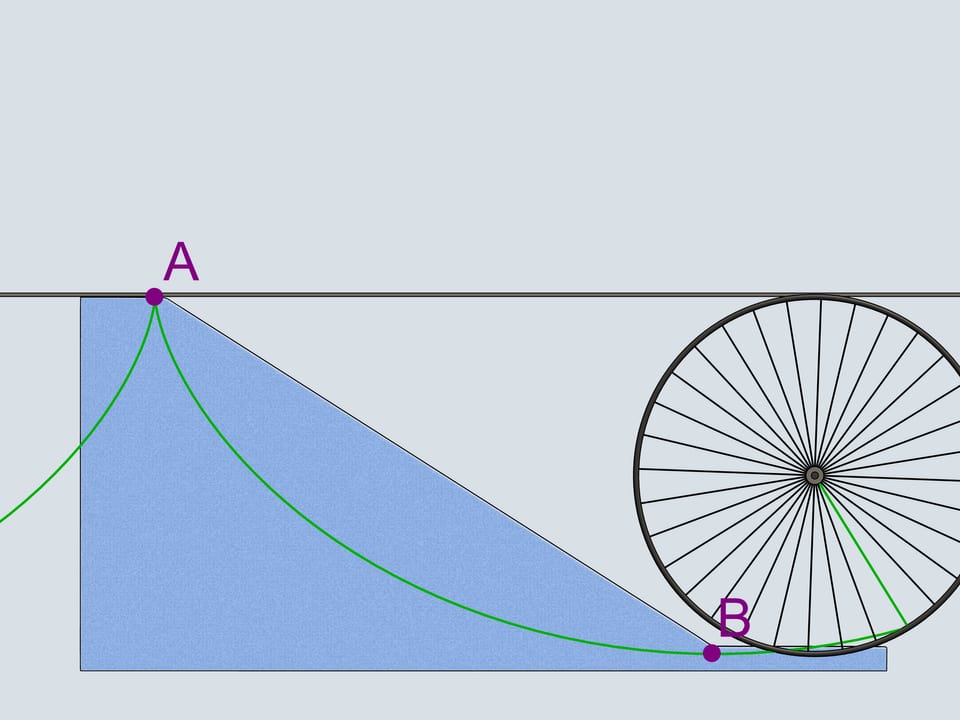
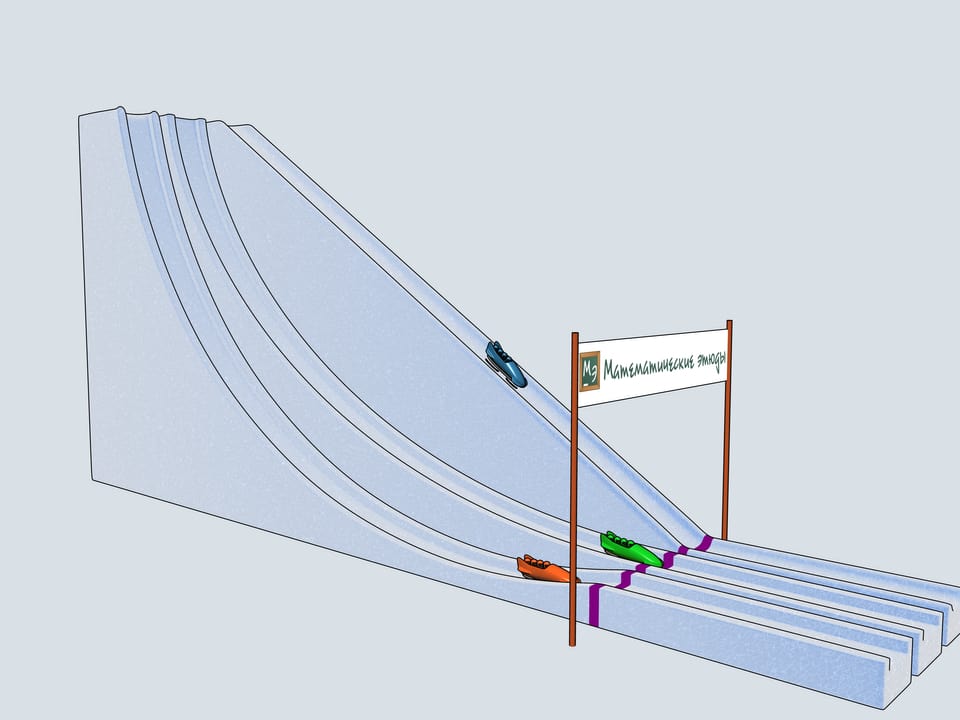
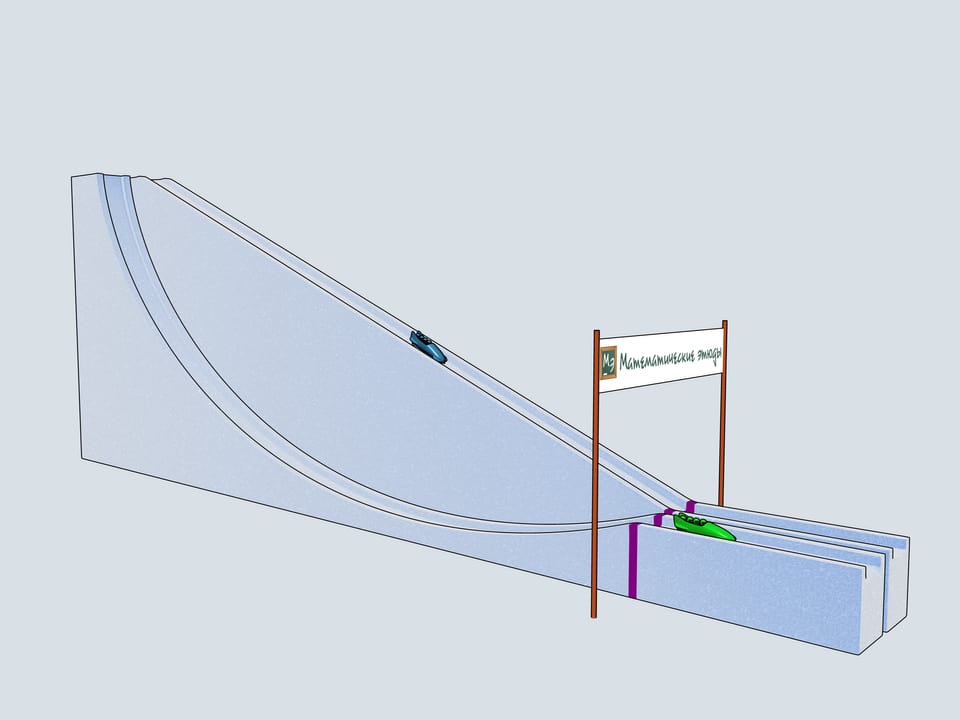
Дадим старт нашим четвёркам. Какой же боб первым приедет к финишу? Боб зелёного цвета, выступающий за команду Математических этюдов и катившийся по циклоидальной горке, приходит первым!

Почему же Галилео Галилей рассматривал четвертинку окружности и считал, что это наилучшая в смысле времени траектория спуска? Он вписывал в неё ломаные и заметил, что при увеличении числа звеньев время спуска уменьшается. Отсюда Галилей естественным образом перешёл к окружности, но сделал неверный вывод, что эта траектория наилучшая среди всех возможных. Как мы видели, наилучшей траекторией является циклоида.

Через две данные точки можно провести единственную циклоиду с условием, что в верхней точке находится точка возврата циклоиды. И даже когда циклоиде приходится подниматься, чтобы пройти через вторую точку, она всё равно будет кривой наискорейшего спуска!

Ещё одна красивая задача, связанная с циклоидой, — задача о таутохроне. В переводе с греческого ταύτίς означает «тот же самый», χρόνος, как мы уже знаем — «время».

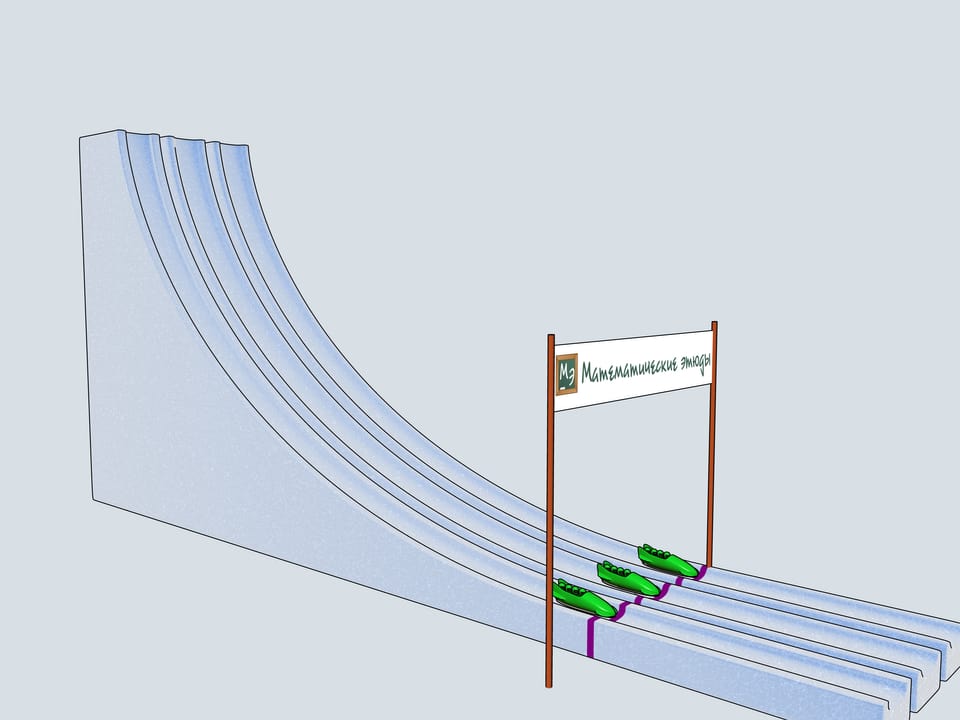
Сделаем три одинаковые горки с профилем в виде циклоиды, так, чтобы концы горок совпадали и располагались в вершине циклоиды. Поставим три боба на разные высоты и дадим отмашку. Удивительнейший факт — все бобы приедут вниз одновременно!

Зимой Вы можете построить во дворе горку изо льда и проверить это свойство вживую.

Задача о таутохроне состоит в нахождении такой кривой, что, начиная с любого начального положения, время спуска в заданную точку будет одинаковым.

Христиан Гюйгенс доказал, что единственной таутохроной является циклоида.

Конечно же, Гюйгенса не интересовал спуск по ледяным горкам. В то время учёные не имели такой роскоши заниматься науками из любви к искусству. Задачи, которые изучались, исходили из жизни и запросов техники того времени. В XVII веке совершаются уже дальние морские плавания. Широту моряки умели определять уже достаточно точно, но удивительно, что долготу не умели определять совсем. И один из предлагавшихся способов измерения широты был основан на наличии точных хронометров.

Первым, кто задумал делать маятниковые часы, которые были бы точны, был Галилео Галилей. Однако в тот момент, когда он начинает их реализовывать, он уже стар, он слеп, и за оставшийся год своей жизни учёный не успевает сделать часы. Он завещает это сыну, однако тот медлит и начинает заниматься маятником тоже лишь перед смертью и не успевает реализовать замысел. Следующей знаковой фигурой был Христиан Гюйгенс.

Он заметил, что период колебания обычного маятника, рассматривавшегося Галилеем, зависит от изначального положения, т.е. от амплитуды. Задумавшись о том, какова должна быть траектория движения груза, чтобы время качения по ней не зависело от амплитуды, он решает задачу о таутохроне. Но как заставить груз двигаться по циклоиде? Переводя теоретические исследования в практическую плоскость, Гюйгенс делает «щёчки», на которые наматывается веревка маятника, и решает ещё несколько математических задач. Он доказывает, что «щёчки» должны иметь профиль той же самой циклоиды, тем самым показывая, что эволютой циклоиды является циклоида с теми же параметрами.

Видео:§4 ЦиклоидаСкачать

Параметрическое уравнение циклоиды и уравнение в декартовых координатах

5. Параметрическое уравнение циклоиды и уравнение в декартовых координатах

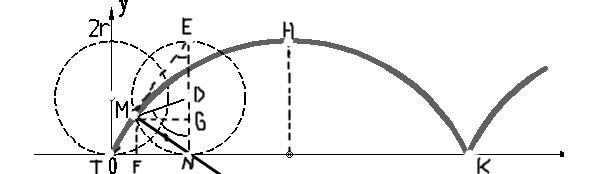
Допустим, что у нас дана циклоида, образованная окружностью радиуса а с центром в точке А.

Если выбрать в качестве параметра, определяющего положение точки, угол t=∟NDM на который успел повернуться радиус, имевший в начале качения вертикально е положение АО, то координаты х и у точки М выразятся следующим образом:

х= OF = ON — NF = NM — MG = at-a sin t,

y= FM = NG = ND – GD = a – a cos t

Итак параметрические уравнения циклоиды имеют вид:

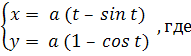
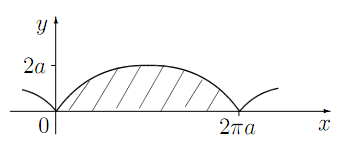
При изменении t от -∞ до +∞ получится кривая, состоящая из бесчисленного множества таких ветвей, какая изображена на данном рисунке.

Так же, помимо параметрического уравнения циклоиды, существует и ее уравнение в декартовых координатах:

, где r – радиус окружности, образующей циклоиду.

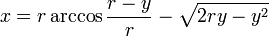
6. Задачи на нахождение частей циклоиды и фигур, образованных циклоидой

Задача №1. Найти площадь фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрически

Решение. Для решения данной задачи, воспользуемся известными нам фактами из теории интегралов, а именно:

Площадь криволинейного сектора.

Рассмотрим некоторую функцию r = r(ϕ), определенную на [α, β].

Будем считать, что r и ϕ — полярные координаты точки. Тогда любому

r₀ — полярные координаты точки. Если ϕ будет меняться, «пробегая» весь[α, β], то переменная точка M опишет некоторую кривую AB, заданную

уравнением r = r(ϕ).

Определение 7.4. Криволинейным сектором называется фигура, ограниченная двумя лучами ϕ = α, ϕ = β и кривой AB, заданной в полярных

координатах уравнением r = r(ϕ), α ≤ ϕ ≤ β.

Теорема. Если функция r(ϕ) > 0 и непрерывна на [α, β], то площадь

криволинейного сектора вычисляется по формуле:

Эта теорема была доказана ранее в теме определенного интеграла.

Исходя из приведенной выше теоремы, наша задача о нахождении площади фигуры, ограниченной одной аркой циклоиды, уравнение которой задано параметрические x= a (t – sin t) , y= a (1 – cos t) , и осью Ох, сводится к следующему решению.

Решение. Из уравнения кривой dx = a(1−cos t) dt. Первая арка циклоиды соответствует изменению параметра t от 0 до 2π. Следовательно,

Задача №2. Найти длину одной арки циклоиды

Так же в интегральном исчислении изучалась следующая теорема и следствие из нее.

Теорема. Если кривая AB задана уравнением y = f(x), где f(x) и f ’ (x) непрерывны на [a, b], то AB является спрямляемой и

Следствие. Пусть AB задана параметрически

L_AB = 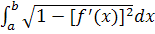(1)

Пусть функции x(t), y(t) непрерывно-дифференцируемые на [α, β]. Тогда

формулу (1) можно записать так

Сделаем замену переменных в этом интеграле x = x(t), тогда y’(x)= ;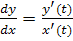

dx= x’(t)dt и, следовательно:

А теперь вернемся к решении нашей задачи.

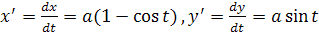
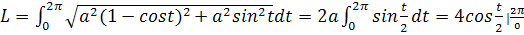
Решение. Имеем , а поэтому

= 8a

Задача №3. Надо найти площадь поверхности S, образованной от вращения одной арки циклоиды

В интегральном исчислении существует следующая формула для нахождения площади поверхности тела вращения вокруг оси х кривой, заданной на отрезке [a,b] параметрически: x=φ(t), y=ψ(t) (t₀ ≤t ≤t₁)

|S|=

Применяя эту формулу для нашего уравнения циклоиды получаем:

Задача №4. Найти объем тела, полученного при вращении арки циклоиды

В интегральном исчислении при изучении объемов есть следующее замечание:

Если кривая, ограничивающая криволинейную трапецию задана параметрическими уравнениями и функции в этих уравнениях удовлетворяют условиям теоремы о замене переменной в определенном интеграле, то объем тела вращения трапеции вокруг оси Ох, будет вычисляться по формуле

Воспользуемся этой формулой для нахождения нужного нам объема.

Итак, в ходе выполнения данной работы были выяснены основные свойства циклоиды. Так же научились строить циклоиду, выяснила геометрический смысл циклоиды. Как оказалось циклоида имеет огромное практическое применение не только в математике, но и в технологических расчетах, в физике. Но у циклоиды есть и другие заслуги. Ею пользовались ученые XVII века при разработке приемов исследования кривых линий, — тех приемов, которые привели в конце концов к изобретению дифференциального и интегрального исчислений. Она же была одним из «пробных камней», на которых Ньютон, Лейбниц и их первые исследователи испытывали силу новых мощных математических методов. Наконец, задача о брахистохроне привела к изобретению вариационного исчисления, столь нужного физикам сегодняшнего дня. Таким образом, циклоида оказалась неразрывно связанной с одним из самых интересных периодов в истории математики.

1. Берман Г.Н. Циклоида. – М., 1980

2. Веров С.Г. Брахистохрона, или еще одна тайна циклоиды // Квант. – 1975. — №5

3. Веров С.Г. Тайны циклоиды// Квант. – 1975. — №8.

4. Гаврилова Р.М., Говорухина А.А., Карташева Л.В., Костецкая Г.С.,Радченко Т.Н. Приложения определенного интеграла. Методические указания и индивидуальные задания для студентов 1 курса физического факультета. — Ростов н/Д: УПЛ РГУ, 1994.

5. Гиндикин С.Г. Звездный век циклоиды // Квант. – 1985. — №6.

6. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. – М.,1969

[1] Такая линия и называется «огибающей». Всякая кривая линия есть огибающая своих касательных.