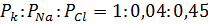Уравнение ходжкина гольдмана для расчета значений потенциалов покоя и действия (6 видео)

Содержание

Природа потенциала покоя мембраны, проницаемой для К+, Na+ и CI . Уравнение Голдмана — Ходжкина — Катца
Потенциал покоя. Уравнение Гольдмана.
Уравнение Гольдмана — Ходжкина — Катца
🎬 Видео

Видео:Потенциал покоя и равновесный потенциалСкачать

Природа потенциала покоя мембраны, проницаемой для К+, Na+ и CI . Уравнение Голдмана — Ходжкина — Катца

Обнаружение проницаемости клеточных мембран к натрию и хлору потребовало пересмотра теории Бернштейна и нового подхода к объяснению природы потенциала покоя. Действительно, содержание солей натрия в 40—50 раз выше в наружной среде, чем в клетке, поэтому, в отличие от калиевого, концентрационный градиент натрия направлен из наружной среды внутрь клетки. Следовательно, при потенциале покоя катионы натрия будут стремиться входить в клетку. Этому будет способствовать не только направленный внутрь концентрационный градиент натрия, но и отрицательный заряд на внутренней стороне мембраны. Такой заряд создается за счет выхода из клетки катионов калия в соответствии с присущим им трансмембранным концентрационным градиентом. Катионы натрия будут постоянно просачиваться в клетку, направляемые и концентрационным градиентом, и градиентом электрического ноля на мембране, При этом катионы Na + будут вносить положительный заряд внутрь и уменьшать электронегативность внутренней стороны мембраны, создаваемую выходом катионов калия.

Анионы хлора также неравномерно распределены между цитоплазмой клетки и наружной средой. Например, у клеток скелетной мускулатуры лягушки концентрация хлора внутри составляет всего 2—5 мМ, а снаружи — около 120 мМ. Это означает, что трансмембранный градиент концентрации хлора направлен из наружной среды внутрь клетки. Под его влиянием анионы хлора могут двигаться через мембрану в клетку, перенося с собой отрицательные заряды и увеличивая величину мембранного потенциала.

Для оценки вклада каждого из потенциал-образующих ионов в формирование потенциала покоя необходимо учитывать такой важный показатель, как проницаемость мембраны. Чем больше будет проницаемость мембраны для конкретного иона, тем легче он будет ее преодолевать и тем больший заряд он будет переносить, участвуя в формировании потенциала покоя.

Теория постоянного поля была разработана Дэвидом Голдманом, Аланом Ходжкиным и Бернардом Катцем. Свое название теория получила из-за предположения о наличии постоянного градиента электрического поля по всей толщине мембраны. При создании этой теории ее авторы постарались преодолеть все противоречия теории Бернштейна. На основе теоретических расчетов Голдмана, Ходжкин и Катц постулировали, что через мембрану клетки в покое текут три независимых друг от друга тока — ток калия наружу, ток натрия внутрь и ток хлора внутрь. Токи обусловлены проницаемостью мембраны к этим ионам и их концентрационными градиентами (рис. 1.4). Совместно эти ионные токи и переносимые ими заряды обеспечивают результирующую зарядку мембраны до величины потенциала покоя. При этом и величина токов, и величина установившегося в результате их взаимовлияния на мембрану потенциала покоя сохраняются постоянными у покоящейся клетки. Это происходит потому, что трансмембранный перепад концентраций ионов не изменяется во времени, а алгебраическая сумма токов при установившемся потенциале равна нулю:

Таким образом, потенциал покоя согласно теории Голдмана — Ходжкина — Катца — это стационарный (постоянный по величине) потенциал, создаваемый одновременной диффузией через мембрану ионов Na + , К + , СЛ в соответствии с их концентрационными градиентами и проницаемостью. Этот потенциал рассчитывают по уравнению Голдмана — Ходжкина — Катца

где Р — проницаемость мембраны для соответствующих ионов, а остальные обозначения — как в уравнении Нернста.

Рис. 1.4. Независимое движение грех ионных токов через мембрану под действием разницы концентраций между цитоплазмой и наружной средой, приводящее к зарядке мембраны и возникновению мембранного

Следует обратить внимание на то, что в числителе уравнения у анионов С1 введена концентрация внутри клетки, а не снаружи, как у катионов К + и Na + . Это связано с отрицательным зарядом анионов С1 — , вследствие чего их ток имеет противоположное направление.

Видео:Физиология. Потенциал действияСкачать

Потенциал покоя. Уравнение Гольдмана.

Между внутренней и внешней стороной клетки всегда есть разность электрических потенциалов. Эта разность в состоянии физиологического покоя клетки называется потенциалом покоя.

Установлено, что возникновение потенциала покоя обусловлено в основном наличием концентрационного градиента ионов калия. Эта точка зрения базируется на том, что ионы калия внутри клетки находятся в свободном состоянии, т.е. не связаны с другими ионами и молекулами и могут свободно диффундировать. Ионы калия диффундируют по концентрационному градиенту через клеточную мембрану и остаются на ее внутренней стороне. Т.к. ионы калия имеют «+» заряд, а анионы «-» заряд, то внешняя поверхность мембраны заряжается положительно, а внутренняя отрицательно.

Понятно, что диффузия продолжается только до тех пор, пока не установится равновесие между силами возникающего электрического поля и силами диффузии.

Мембрана в состоянии покоя проницаема не только для ионов калия, но и в небольшой степени для ионов натрия и хлора. Мембранный потенциал клеток представляет собой результирующую электродвижущих сил, генерируемых всеми этими каналами диффузии. Возникающий при этом потенциал описывается уравнением Гольдмана – Ходжкина – Катца:

где – коэффициенты проницаемости мембраны для ионов .

— концентрация ионов внутри ( ) и вне ( ) клетки.

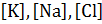
Таким образом, величина потенциала покоя клетки определяется двумя основными факторами:

1. соотношением концентраций проникающих через покоящуюся мембрану катионов и анионов;

2. соотношением проницаемостей мембраны для этих ионов.

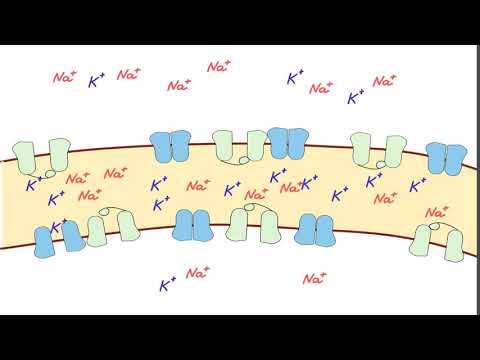
Состояние покоя характеризуется следующим отношением ионных проницаемостей:

Уравнение Гольдмана переходит в уравнение Нернста, если мембрана проницаема для одного вида ионов. Следует отметить, что наличие обменной диффузии не влияет на мембранный потенциал.

Наиболее распространенный метод измерения биопотенциала покоя – микроэлектродный. При этом микроэлектроды вводятся: первый непосредственно в цитоплазму клетки, второй – во внеклеточную жидкость. Установлено, что цитоплазма в состоянии покоя клеток всегда имеет отрицательный потенциал по отношению к потенциалу межклеточной жидкости и колеблется в пределах от -100 милливольт до -50 милливольт.

6.3. Потенциал действия. Потенциал действия аксона нервной клетки.Уравнение Ходжкина – Хаксли.

Общее изменение разности потенциалов между клеткой и средой, происходящее при возбуждении клетки, называется потенциалом действия. В его основе лежат изменения ионной проницаемости мембраны. Потенциалы действия обеспечивают проведение возбуждения по нервным волокнам и инициируют процессы сокращения мышечных и секреции железистых клеток.

Представим график потенциала действия аксона нервной клетки. Потенциал как функция времени показан в фиксированной точке аксона.

φ₁= -70 мВ потенциал покоя

φ₂= +40 мВ мембранный потенциал при возбуждении

φ₃ = /φ₁/+ φ₂ =110 мВ потенциал действия

φ₄=-30 мВ запаздывающий потенциал.

Представим схему развития и распространения потенциала действия по аксону нервной клетки:

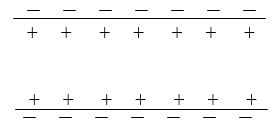
1. Состояние покоя.

Положительные и отрицательные заряды равномерно распределены вдоль аксона. Потенциал покояφ₁= -70 мВ.

2. Приложен стимул.

Происходит увеличение проницаемости мембраны для ионов натрия, примерно в 5000 раз. Поток ионов натрия из межклеточного пространства перекрывает отрицательный потенциал клетки и разрушает локальный положительный потенциал. Этот потенциал возникает в доли секунды и вырастает до φ₂=40мВ и называется потенциалом действияφ₃=110 мВ

3. Распространение потенциала действия.

Перемена мембранного потенциала называется деполяризацией. Эффект деполяризации, возникший в одной точке, индуцирует деполяризацию с обеих сторон от возбужденной точки.

Возникшее однажды значение потенциала действия распространяется по аксону до тех пор, пока не деполяризуется весь участок.

4. Полная деполяризация участка аксона.

Почти сразу же после деполяризации мембрана приходит в исходное состояние с низкой проницаемости для ионов натрия.

5. Начало реполяризации.

Происходит резкое увеличение проницаемости мембраны для ионов калия. Ионы калия диффундируют из клетки, и это приводит к понижению потенциала клетки до отрицательных значений.

«Ворота» для калия остаются открытыми в течение всего процесса реполяризации и, следовательно, потенциал падает ниже потенциала покоя и составляет минус 100 мВ. Клетка приходит в исходное состояние за 10 мсек.

Таким образом, формирование потенциала действия обусловлено двумя ионными потоками через мембрану: поток ионов натрия внутрь клетки приводит к перезарядке мембраны, а противоположно направленный поток ионов калия обуславливает восстановление исходного потенциала покоя.

Общее изменение мембранного потенциала при возбуждении складывается из потенциала покоя и мембранного потенциала при возбуждении .Потенциал действия рассчитывается по уравнению Ходжкина – Хаксли.

В состоянии возбуждения, отвечающим генерации потенциала действия, отношение ионных проницаемостей, следующее:

Потенциал действия функционирует по принципу «все или ничего» т.е. процесс либо происходит до конца, либо не начинается. Если стимул имеет величину, достаточную для запускания потенциала действия, то потенциал имеет одинаковую амплитуду и форму независимо от типа, величины и продолжительности действия стимула.

Скорость, с которой потенциал действия распространяется вдоль нервного волокна, зависит от диаметра волокна и от того покрыт ли аксон слоем миелина (структура из липопротеидов). У небольших волокон без миелина скорость может быть меньше 0,5 м/с, в то время как для больших волокон, покрытых миелином, скорость может быть 130 м/с. Ясно, что нервные импульсы не распространяются подобно электрическим сигналам. Распространение нервного импульса – это сложный электрохимический процесс, детали которого подробно рассматриваются при изучении таких дисциплин, как биохимия, физиология, нервные болезни.

Видео:Мембранные потенциалы - Часть 1Скачать

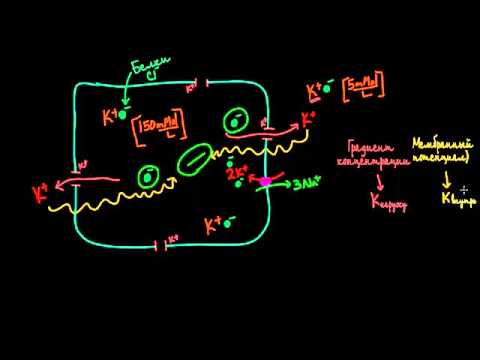
Уравнение Гольдмана — Ходжкина — Катца

Трудность применения уравнения Нернста — Планка (4.4) к биологической мембране (даже в случае одномерного ее описания) состоит в том, что изменения величин с или ф внутри мембраны неизвестны и зависят от существующих пространственных электрических зарядов. Однако поскольку мембрана тонка, в качестве хороше

Рис. 4.5. Одномерная модель мембраны с линейным изменением трансмембранного потенциала для вывода уравнения Голъдмана — Ходжкина — Катца

го приближения можно взять линейный закон изменения ф внутри мембраны.

Это предположение было использовано Гольдманом, чтобы проинтегрировать уравнение Нернста — Планка. Проделаем это для мембраны в стационарных условиях, например, для мембраны в состоянии покоя. В одномерном случае, представленном на рис. 4.5, в стационарных условиях имеем

где V_m — трансмембранный потенциал и d — толщина мембраны. Для простоты рассмотрим одновалентные катионы.

Поскольку Уф = —, Vc = —, из уравнения (4.4) получаем dx dx

для потока иона данного сорта через единицу площади поверхности следующее выражение:

В частности, для иона калия при допущении постоянства поля (4.53) получим:

Преобразование уравнения (4.53) дает

Теперь произведем интегрирование по толщине мембраны от ее левого края (х = 0) до правого края (х = d). Поскольку величина j_K постоянна в силу условия стационарности, а величина D_K просто предполагается постоянной, в левой части уравнения (4.56) переменной является с_к(х). Следовательно,

Решение уравнения (4.57) относительноу’_к Д ает

Концентрация калия в общей объемной среде связана с концентрацией внутри мембраны через посредство коэффициентов распределения р. В уравнении (4.58) имеются ввиду внутримембранные концентрации. Предполагается, что коэффициенты (3 на обеих поверхностях раздела одинаковы. Следовательно, если обозначим индексом «0» поверхность мембраны, контактирующую с внутриклеточным пространством, а индексом d — поверхность в контакте с внеклеточной средой (см. рис. 4.5), то

где [К + ] — концентрация калия в общей объемной среде.

Учитывая, что /_к =/ (/_К) и введя определение проницаемости для калия Р_к как

из уравнения (4.58) находим:

здесь индексы I и II относятся соответственно к вне- и внутриклеточной концентрациям.

Аналогичные выражения можно получить для J_Na и J_C) — плотностей натриевого и хлорного токов, которые вместе с калиевым играют важную роль в функционировании биологических мембран. Выражение для J_C1 несколько отличается, поскольку речь идет об анионе. Полная плотность ионного тока равна сумме отдельных ионных компонент, т. е.

Уравнение (4.61) можно переписать в виде где

В общем случае биологическая мембрана не может быть в равновесии для всех ионов. Если вычислить потенциалы Нернста для К, Na, Cl при их обычных концентрациях, то полученные величины окажутся различными. Таким образом, никакой трансмембранный потенциал не может одновременно уравновесить все ионы. Условие покоя может быть охарактеризовано только как стационар- dV

ное состояние ( m = 0). При этом требуется выполнение равенст- ot

ва J— 0 и подразумевается, что w — ye RT =0. Последнее условие позволяет найти решение для трансмембранного потенциала покоя

Уравнение (4.66) называется уравнением Гольдмана -Ходжкина -Катца. Будем применять его как к невозбудимой, так и к возбудимой мембране, но лишь при условии, что 7=0.

В случае, когда проницаемость мембраны для ионов натрия и хлора значительно меньше проницаемости для калия Рш Рк и Р_С + -К + -АТФаза работает в режиме, когда т = 3/2; т всегда больше 1. (Нет ионных насосов, перекачивающих С1“, поэтому в уравнении Томаса отсутствуют члены / ci[Cl — ]).

Коэффициент т > 1 усиливает вклад градиента концентрации калия в создание мембранного потенциала, поэтому мембранный потенциал, рассчитанный по Томасу, больше по абсолютной величине, чем мембранный потенциал, рассчитанный по Гольдману, и дает совпадение с экспериментальными значениями для мелких клеток.

Нарушение биоэнергетических процессов в клетке и работы Ыа + -К + -АТФазы приводят к уменьшению V_m, в этом случае мембранный потенциал лучше описывается уравнением Г ольдмана.

В создании потенциала покоя роль иона хлора по сравнению с ролью иона калия представляется второстепенной. Это связано с тем, что внутриклеточная концентрация хлора очень мала и при малом притоке или оттоке ионов подвергается большим относительным изменениям хлора (для калия дело обстоит иначе). Следовательно, можно ожидать, что движения иона хлора будут приводить его концентрации по обе стороны мембраны в соответствие с практически фиксированным отношением концентраций нона калия, т. е. будут направлены на выравнивание потенциалов Нернста. Два отношения ионных концентраций согласуются друг с другом, если

Рис. 4.6. Направление ионных потоков в мембране

[К + ]_п [С1“]п = [K + ]j [С1 — ]_ь что одновременно является условием дон- нановского равновесия.

Связь трансмембранного потенциала покоя V_m с внеклеточной концентрацией калия экспериментально исследовали Ходжкин и Хо- рович. Эта связь воспроизводится на рис. 4.7. Заметим, что для [К + ],> 10 ммоль/л существует линейная зависимость V_m от логарифма [К + ]_ь как и предсказывает уравнение Нернста для калия (4.69).

Для [K + ]j + ]_T /[К + ]_г + ]_Ib очевидно, пренебрежимо мала). Тем не менее, если [К 1i + ]j в потенциал покоя необходимо учитывать. Результат показан на рис. 4.7. Кривая, построенная по уравнению (4.69), согласуется с экспериментальными данными достаточно хорошо даже при [К + ф + ]j = 2,5 ммоль/л и [Cl

]j = 120 ммоль/л. Внутриклеточная концентрация калия была равна [К + ]_п= 140 ммоль/л, внутриклеточная концентрация хлора [Cl“]i = 24 ммоль/л, и потенциал покоя был равен номинальному равновесному потенциалу для хлора — 98,5 мВ.

Если в момент времени t = 0 быстро уменьшали внеклеточную концентрацию хлора до 30 ммоль/л (рис. 4.8), то результатом было увеличение V® на 58 lg(l 20/30) = 34,9 мВ, так что величина V® возрастала от — 98,5 до — 63,6 мВ. Экспериментально было установлено, что мембранный потенциал возрос до — 77 мВ (рис. 4.8). (Заметим, что эта величина лежит между V® = — 98,5мВ и V® = — 63 мВ.)

После уменьшения внеклеточной концентрации хлора возникает поток С1

наружу, обусловленный электрическим полем, которое более не компенсируется диффузией внутрь, и это вызывает увеличение V_m. В результате увеличения направленного наружу электрического поля ионы К+ движутся наружу, вызывая отток КС1

Рис. 4.7. Влияние внеклеточной концентрации иона калия по оси абсцисс на мембранный потенциал (по оси ординат) изолированного волокна мышцы лягушки. Внеклеточные растворы не содержали хлора, главным анионом был сульфат

Рис. 4.8. Влияние внезапного уменьшения внеклеточной концентрации хлора на мембранный потенциал изолированного волокна мышцы лягушки

из клетки. Фактически, как видим, лишь очень малый поток одного иона может иметь место без возникновения дополнительных (уравновешивающих) полей. Иллюстрацией этого положения может служить наблюдаемый здесь поток, который по существу электроней- трален, с равными количествами ионов калия и хлора.

Чтобы установились равные потоки калия и хлора, силы, действующие на каждый из ионов, должны быть обратно пропорциональны проводимостям. Таким образом, поскольку АV* = (98,5-77)- движущая сила для калия (разность между V_m и V* при t = 0), а =(77 — 63,6) — движущая сила для хлора (V_m — V^ 1 ), то для простоты полагаем, что

Результатом оттока КС1 является очень слабое уменьшение концентрации [К + ]_п (от 140 до 138 ммоль/л) и, следовательно, очень небольшое изменение V_nf Тем не менее, концентрация [С1 ]_п подвергается большому относительному изменению. В конце концов (примерно за 15 мин) V™ уменьшается до уровня, определяемого величиной V* (по мере того как [С1

]| уменьшается из-за оттока хлора).

Если предположить, что значение = — 98,5 мВ и остается неизменным, концентрация [С1

]п должна упасть в 4 раза, чтобы компенсировать уменьшение [(ГЕф в 4 раза (от 120 до 30 ммоль/л). Это равновесие достигается, когда [С1 _ ]_п падает до 0,6 ммоль/л с начального уровня 2,4 ммоль/л — снижение на 1,8 ммоль/л. Таким образом, отток КС1 составляет 1,8 ммоль/л, тогда как внутриклеточная концентрация калия уменьшается от 140 до 138 ммоль/л, что, как уже отмечалось, пренебрежимо мало влияет на V_nf. Следовательно, оказывается, что и, в самом деле, хлор подстраивается к изменившимся условиям и остается в равновесии, а задание уровня потенциала покоя приходится на долю калия.

Почему считается, что выход 1,8 ммоль/л не влияет на значение [К + ф.Потому, что внеклеточное пространство содержит очень большой объем электролита, и выходящие ионы оказывают лишь слабое влияние на общую концентрацию в этом пространстве. Большой внеклеточный объем резко отличается от ограниченного внутриклеточного пространства.