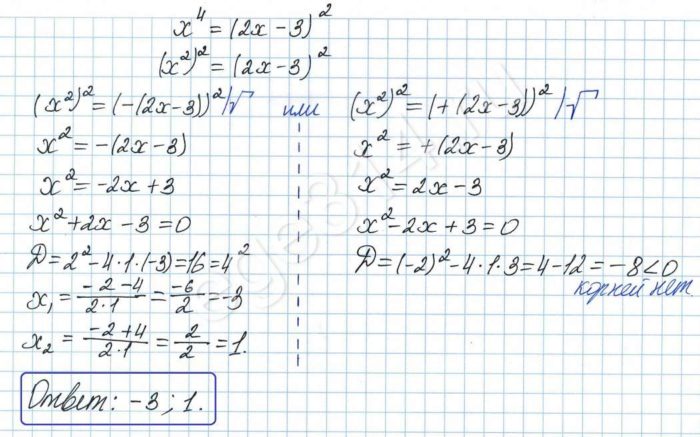Уравнение х в 4 степени равно 2х 3 квадрате

Видео:КАК РЕШАТЬ КУБИЧЕСКИЕ УРАВНЕНИЯ | Разбираем на конкретном примереСкачать

x^4=(2*x-3)^2 (уравнение)

Найду корень уравнения: x^4=(2*x-3)^2

Решение

Дано уравнение:
$$x^ = left(2 x — 3right)^$$
преобразуем:
Вынесем общий множитель за скобки
$$left(x — 1right) left(x + 3right) left(x^ — 2 x + 3right) = 0$$
Т.к. правая часть ур-ния равна нулю, то решение у ур-ния будет, если хотя бы один из множителей в левой части ур-ния равен нулю.
Получим ур-ния
$$x — 1 = 0$$
$$x + 3 = 0$$
$$x^ — 2 x + 3 = 0$$
решаем получившиеся ур-ния:
1.
$$x — 1 = 0$$
Переносим свободные слагаемые (без x)
из левой части в правую, получим:
$$x = 1$$
Получим ответ: x1 = 1
2.
$$x + 3 = 0$$
Переносим свободные слагаемые (без x)
из левой части в правую, получим:
$$x = -3$$
Получим ответ: x2 = -3
3.
$$x^ — 2 x + 3 = 0$$
Это уравнение вида

Квадратное уравнение можно решить
с помощью дискриминанта.
Корни квадратного уравнения:
$$x_ = frac <sqrt- b>$$
$$x_ = frac <- sqrt- b>$$
где D = b^2 — 4*a*c — это дискриминант.
Т.к.
$$a = 1$$
$$b = -2$$
$$c = 3$$
, то

© Контрольная работа РУ — калькуляторы онлайн

Видео:Уравнение четвертой степениСкачать

Где учитесь?

Для правильного составления решения, укажите:

Видео:Неполные квадратные уравнения. Алгебра, 8 классСкачать

Решение №1178 Решите уравнение х^4 = (2х – 3)^2

Решите уравнение х 4 = (2х – 3) 2

Источник задания: ОГЭ 2021 Математика, И.В. Ященко. 36 вариантов.

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 4.6 / 5. Количество оценок: 21

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.

Видео:Решите уравнение x^2+3x=54. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

Решение уравнений четвертой степени

Для уравнений четвертой степени применимы все те общие схемы решения уравнений высших степеней, что мы разбирали в предыдущем материале. Однако существует ряд нюансов в решении двучленных, биквадратных и возвратных уравнений, на которых мы хотели бы остановиться подробнее.

Также в статье мы разберем искусственный метод разложения многочлена на множители, решение в радикалах и метод Феррари, который используется для того, чтобы свести решение уравнения четвертой степени к кубическому уравнению.

Видео:Математика | Кубические уравнения по методу СталлонеСкачать

Решение двучленного уравнения четвертой степени

Это простейший тип уравнений четвертой степени. Запись уравнения имеет вид A x 4 + B = 0 .

Для решения этого типа уравнений применяются формулы сокращенного умножения:

A x 4 + B = 0 x 4 + B A = 0 x 4 + 2 B A x 2 + B A — 2 B A x 2 = 0 x 2 + B A 2 — 2 B A x 2 = 0 x 2 — 2 B A 4 x + B A x 2 + 2 B A 4 x + B A = 0

Остается лишь найти корни квадратных трехчленов.

Решить уравнение четвертой степени 4 x 4 + 1 = 0 .

Решение

Для начала проведем разложение многочлена 4 x 4 + 1 на множители:

4 x 4 + 1 = 4 x 4 + 4 x 2 + 1 = ( 2 x 2 + 1 ) 2 — 4 x 2 = 2 x 2 — 2 x + 1 ( 2 x 2 + 2 x + 1 )

Теперь найдем корни квадратных трехчленов.

2 x 2 — 2 x + 1 = 0 D = ( — 2 ) 2 — 4 · 2 · 1 = — 4 x 1 = 2 + D 2 · 2 = 1 2 + i x 2 = 2 — D 2 · 2 = 1 2 — i

2 x 2 + 2 x + 1 = 0 D = 2 2 — 4 · 2 · 1 = — 4 x 3 = — 2 + D 2 · 2 = — 1 2 + i x 4 = — 2 — D 2 · 2 = — 1 2 — i

Мы получили четыре комплексных корня.

Ответ: x = 1 2 ± i и x = — 1 2 ± i .

Видео:5 способов решения квадратного уравнения ➜ Как решать квадратные уравнения?Скачать

Решение возвратного уравнения четвертой степени

Возвратные уравнения четвертого порядка имеют вид A x 4 + B x 3 + C x 2 + B x + A = 0

х = 0 не является корнем этого уравнения: A · 0 4 + B · 0 3 + C · 0 2 + B · 0 + A = A ≠ 0 . Поэтому на x 2 можно смело разделить обе части этого уравнения:

A x 4 + B x 3 + C x 2 + B x + A = 0 A x 2 + B x + C + B x + A x 2 = 0 A x 2 + A x 2 + B x + B x + C = 0 A x 2 + 1 x 2 + B x + 1 x + C = 0

Проведем замену переменных x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2 :

A x 2 + 1 x 2 + B x + 1 x + C = 0 A ( y 2 — 2 ) + B y + C = 0 A y 2 + B y + C — 2 A = 0

Так мы проведи сведение возвратного уравнения четвертой степени к квадратному уравнению.

Найти все комплексные корни уравнения 2 x 4 + 2 3 + 2 x 3 + 4 + 6 x 2 + 2 3 + 2 x + 2 = 0 .

Решение

Симметрия коэффициентов подсказывает нам, что мы имеем дело с возвратным уравнением четвертой степени. Проведем деление обеих частей на x 2 :

2 x 2 + 2 3 + 2 x + 4 + 6 + 2 3 + 2 x + 2 x 2 = 0

2 x 2 + 2 x 2 + 2 3 + 2 x + 2 3 + 2 x + 4 + 6 + = 0 2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0

Проведем замену переменной x + 1 x = y ⇒ x + 1 x 2 = y 2 ⇒ x 2 + 1 x 2 = y 2 — 2

2 x 2 + 1 x 2 + 2 3 + 2 x + 1 x + 4 + 6 = 0 2 y 2 — 2 + 2 3 + 2 y + 4 + 6 = 0 2 y 2 + 2 3 + 2 y + 6 = 0

Решим полученное квадратное уравнение:

D = 2 3 + 2 2 — 4 · 2 · 6 = 12 + 4 6 + 2 — 8 6 = = 12 — 4 6 + 2 = 2 3 — 2 2 y 1 = — 2 3 — 2 + D 2 · 2 = — 2 3 — 2 + 2 3 — 2 4 = — 2 2 y 2 = — 2 3 — 2 — D 2 · 2 = — 2 3 — 2 — 2 3 + 2 4 = — 3

Вернемся к замене: x + 1 x = — 2 2 , x + 1 x = — 3 .

Решим первое уравнение:

x + 1 x = — 2 2 ⇒ 2 x 2 + 2 x + 2 = 0 D = 2 2 — 4 · 2 · 2 = — 14 x 1 = — 2 — D 2 · 2 = — 2 4 + i · 14 4 x 2 = — 2 — D 2 · 2 = — 2 4 — i · 14 4

Решим второе уравнение:

x + 1 x = — 3 ⇒ x 2 + 3 x + 1 = 0 D = 3 2 — 4 · 1 · 1 = — 1 x 3 = — 3 + D 2 = — 3 2 + i · 1 2 x 4 = — 3 — D 2 = — 3 2 — i · 1 2

Ответ: x = — 2 4 ± i · 14 4 и x = — 3 2 ± i · 1 2 .

Видео:ОГЭ №21 Как решать кубическое уравнение x^3+4x^2-9x-36=0 Группировка Деление многочлена столбикомСкачать

Решение биквадратного уравнения

Биквадратные уравнения четвертой степени имеют вид A x 4 + B x 2 + C = 0 . Мы можем свести такое уравнение к квадратному A y 2 + B y + C = 0 путем замены y = x 2 . Это стандартный прием.

Решить биквадратное уравнение 2 x 4 + 5 x 2 — 3 = 0 .

Решение

Выполним замену переменной y = x 2 , что позволит нам свести исходное уравнение к квадратному:

2 y 2 + 5 y — 3 = 0 D = 5 2 — 4 · 2 · ( — 3 ) = 49 y 1 = — 5 + D 2 · 2 = — 5 + 7 4 = 1 2 y 2 = — 5 — D 2 · 2 = — 5 — 7 4 = — 3

Следовательно, x 2 = 1 2 или x 2 = — 3 .

Первое равенство позволяет нам получить корень x = ± 1 2 . Второе равенство не имеет действительных корней, зато имеет комплексно сопряженных корней x = ± i · 3 .

Ответ: x = ± 1 2 и x = ± i · 3 .

Найти все комплексные корни биквадратного уравнения 16 x 4 + 145 x 2 + 9 = 0 .

Решение

Используем метод замены y = x 2 для того, чтобы свести исходное биквадратное уравнение к квадратному:

16 y 2 + 145 y + 9 = 0 D = 145 2 — 4 · 16 · 9 = 20449 y 1 = — 145 + D 2 · 16 = — 145 + 143 32 = — 1 16 y 2 = — 145 — D 2 · 16 = — 145 — 143 32 = — 9

Поэтому, в силу замены переменной, x 2 = — 1 16 или x 2 = — 9 .

Ответ: x 1 , 2 = ± 1 4 · i , x 3 , 4 = ± 3 · i .

Видео:Функция у=х² и у=х³ и их графики. Алгебра, 7 классСкачать

Решение уравнений четвертой степени с рациональными корнями

Алгоритм нахождения рациональных корней уравнения четвертой степени приведен в материале «Решение уравнений высших степеней».

Видео:Как решать любое квадратное уравнение Полное Неполное квадр ур x^2+2x-3=0 5x^2-2x=0 2x^2-2=0 3x^2=0Скачать

Решение уравнений четвертой степени по методу Феррари

Уравнения четвертой степени вида x 4 + A x 3 + B x 2 + C x + D = 0 в общем случае можно решить с применением метода Феррари. Для этого необходимо найти y 0 . Это любой из корней кубического уравнения y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 . После этого необходимо решить два квадратных уравнения x 2 + A 2 x + y 0 2 + A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 , у которых подкоренное выражение является полным квадратом.

Корни, полученные в ходе вычислений, будут корнями исходного уравнения четвертой степени.

Найти корни уравнения x 4 + 3 x 3 + 3 x 2 — x — 6 = 0 .

Решение

Имеем А = 3 , В = 3 , С = — 1 , D = — 6 . Применим метод Феррари для решения данного уравнения.

Составим и решим кубическое уравнение:
y 3 — B y 2 + A C — 4 D y — A 2 D + 4 B D — C 2 = 0 y 3 — 3 y 2 + 21 y — 19 = 0

Одним из корней кубического уравнения будет y 0 = 1 , так как 1 3 — 3 · 1 2 + 21 · 1 — 19 = 0 .

Запишем два квадратных уравнения:
x 2 + A 2 x + y 0 2 ± A 2 4 — B + y 0 x 2 + A 2 y 0 — C x + y 0 2 4 — D = 0 x 2 + 3 2 x + 1 2 ± 1 4 x 2 + 5 2 x + 25 4 = 0 x 2 + 3 2 x + 1 2 ± 1 2 x + 5 2 2 = 0

x 2 + 3 2 x + 1 2 + 1 2 x + 5 2 = 0 или x 2 + 3 2 x + 1 2 — 1 2 x — 5 2 = 0

x 2 + 2 x + 3 = 0 или x 2 + x — 2 = 0

Корнями первого уравнения будут x = — 1 ± i · 2 , корнями второго х = 1 и х = — 2 .

Ответ: x 1 , 2 = — 1 ± i 2 , x 3 = 1 , x 4 = — 2 .

🎦 Видео

№5 Линейное уравнение 2-3(2х+2)=5-4х Простое уравнение со скобками 6кл 7кл 8кл 9кл 11кл ОГЭ ЕГЭСкачать

Как решать уравнения 4 степени Решите уравнение четвертой степени Разложить на множители Безу столбиСкачать

Алгебра 8 класс (Урок№19 - Уравнение х² = а.)Скачать

Решение тригонометрических уравнений. Подготовка к ЕГЭ | Математика TutorOnlineСкачать

Как решать кубические уравнения Решите уравнение 3 степени 9 класс Разложить на множители ДелениеСкачать

Сложные уравнения. Как решить сложное уравнение?Скачать

Решение уравнений в несколько действий. Как объяснить ребенку решение уравнений?Скачать

Cистемы уравнений. Разбор задания 6 и 21 из ОГЭ. | МатематикаСкачать

Решите уравнение (x+3)^2=(x+8)^2. | ОГЭ 2017 | ЗАДАНИЕ 4 | ШКОЛА ПИФАГОРАСкачать

Решаем быстро и красиво ★ Уравнение четвертой степени ★ x^4+8x-7=0Скачать

Подготовка к ОГЭ. Задание 21. Решить уравнение x^4=(2x-15)^2Скачать