Уравнение гравитации земли и луны

Видео:Физика с нуля: О чем ЗАКОН ВСЕМИРНОГО ТЯГОТЕНИЯ — Самое простое и понятное объясненияСкачать

Уравнение гравитации земли и луны

В данной главе мы рассмотрим, как Луна воздействует своим гравитационным полем собственно на саму Землю, т.е. на ее тело и ее движение по орбите. Последствия данного воздействия для различных земных сфер — литосферы, гидросферы, ядра, атмосферы, магнитосферы и др., а также для биосферы будут рассмотрены в следующих главах.

ВНИМАНИЕ!
Графики гравитационного взаимодействия Луны и Земли см. с помощью сервиса
ЛУННЫЙ ФАКТОР

3.1. ПАРАМЕТРЫ ЛУННОЙ ГРАВИТАЦИИ.

Расчетные соотношения и константы

Для расчета гравитационного воздействия Луны воспользуемся формулой классической физики, определяющей силу F взаимного притяжения двух тел с массами M1 и M2, центры масс которых находятся друг от друга на расстоянии R:

(1) F (н) = (G x M1 x M2) / R 2 ,

где G = 6,67384 х 10 -11 — гравитационная постоянная.

Данная формула дает значение силы притяжения в единицах системы СИ — ньютонах (н). Для целей нашего трактата удобнее и понятнее будет оперировать килограммами силы (кгс), которые получаются делением F на коэффициент 9,81, т.е.:

(2) F (кгс) = (G x M1 x M2) / (9,81 х R 2 )

Для дальнейших расчетов нам потребуются следующие константы:

1. масса Луны — 7,35 х 10 22 кг;
2. среднее расстояние от Земли до Луны — 384400 км;
3. средний радиус Земли — 6371 км;
4. масса Солнца — 1,99 х 10 30 кг;
5. среднее расстояние от Земли до Солнца — 149,6 млн. км;

Сила лунного притяжения на Земле

В соответствии с формулой (2), сила притяжения Луной тела массой 1 кг, находящегося в центре Земли, при расстоянии между Луной и Землей, равном его среднему значению, равна:

(3) F = (6,67 х 10 -11 х 7,35 х 10 22 х 1) / (9,81 х 384400000 2 ) = 0, 000003382 кгс

т.е. всего 3,382 микрограмма. Для сравнения расчитаем силу притяжения того же тела Солнцем (также для среднего расстояния):

(4) F = (6,67 х 10 -11 х 1,99 х 10 30 х 1) / (9,81 х 149600000000 2 ) = 0, 000604570 кгс,

т.е. 604,570 микрограмм, что почти в 200 (двести!) раз больше, чем сила притяжения Луной.

Кроме того, вес тела, находящегося на поверхности Земли, изменяется в гораздо более существенных пределах из-за отклонения формы Земли от идеальной, неравномерности рельефа и плотности, а также влияния центробежных сил. Так, например, вес тела массой в 1 кг на полюсах больше веса на экваторе примерно на 5,3 грамма, причем одна треть этой разницы обусловлена сплюснутостью Земли с полюсов, а две трети — центробежной силой на экваторе, направленной против силы тяжести.

Как видно, прямое гравитационное воздействие Луны на конкретное тело, находящееся на Земле, является в прямом смысле микроскопическим и при этом существенно уступает гравитационному воздействию Солнца и геофизических аномалий.

Градиент силы лунного притяжения

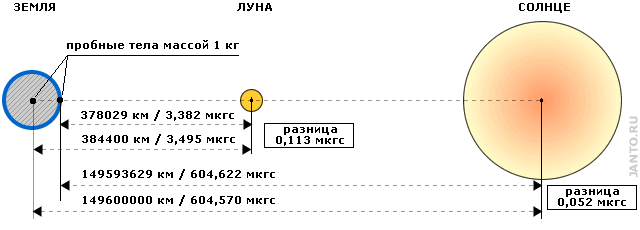
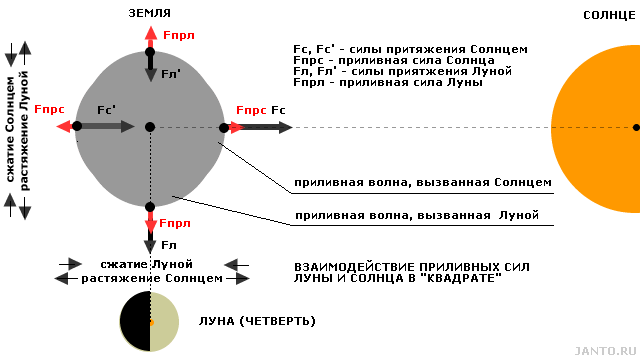
Обратимся к рис.3.1. Для среднего значения расстояния Земля — Луна сила притяжения Луной тела массой 1 кг, расположенного на поверхности Земли в ближайшей к Луне точке составляет 3,495 микрограмм, что на 0,113 микрограмм больше, чем сила притяжения того же тела, но расположенного в центре Земли. Сила же притяжения тела, находящегося на поверхности Земли, Солнцем (также для среднего значения расстояния) составит 604,622 микрограмма, что больше силы притяжения того же тела, но расположенного в центре Земли, на 0,052 микрограмма.

Рис.3.1 Лунная и солнечная гравитация

Т.о, несмотря на неизмеримо меньшую массу Луны по сравнению с Солнцем, градиент силы ее тяготения на орбите Земли в среднем в два с лишним раза больше градиента силы тяготения Солнца.

3.2. ВЛИЯНИЕ НА ТЕЛО ЗЕМЛИ

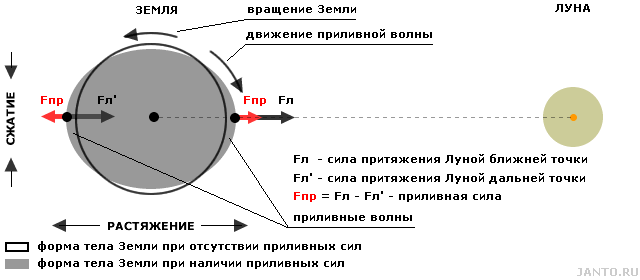
Для иллюстрации воздействия гравитационного поля Луны на тело Земли обратимся к рис. 3.2.

Рис.3.2 Влияние гравитационного поля Луны на тело Земли.

Данный рисунок представляет весьма и весьма упрощенную картину реакции тела Земли на воздействие лунной гравитации, но достоверно отражает суть процесса — изменение формы земного шара под воздействием т.н. приливных (или приливообразующих) сил, направленных вдоль оси Земля — Луна, и противодействующих им сил упругости тела Земли. Приливные силы возникают из-за того, что точки Земли, расположенные ближе к Луне, притягиваются к ней сильнее, чем точки, расположенные дальше от нее. Иными словами, деформация тела Земли является следствием градиента силы притяжения Луны и противодействующих ему сил упругости тела Земли. В результате действия этих сил размер Земли увеличивается в направлении действия приливных сил и уменьшается в поперечном направлении, вследствие чего на поверхности образуется волна, именуемая приливной. Эта волна имеет два максимума, находящиеся на оси Земля — Луна и перемещающиеся по поверхности Земли в направлении, противоположном направлению ее вращения. Амплитуда волны зависит от широты местности и текущих параметров орбиты Луны и может достигать нескольких десятков сантиметров. Максимальное значение она будет иметь на экваторе при прохождении Луной ее перигея.

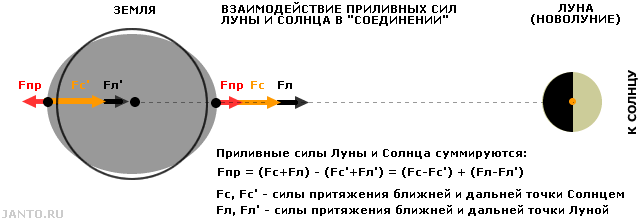
Солнце также вызывает приливную волну в теле Земли, но существенно меньшую из-за меньшего градиента силы его тяготения. Совместное гравитационное воздействие Луны и Солнца на тело Земли зависит от их взаимного расположения. Максимально значение приливных сил и, соответственно, максимальная амплитуда приливной волны достигается при расположении всех трех объектов на одной оси, т.е. в состоянии т.н. сизигии (выравнивания), что имеет место при новолунии (Луна и Солнце в «соединении») или при полнолунии (Луна и Солнце в «оппозиции»). Данные конфигурации иллюстрируются рис. 3.3 и 3.4.

Рис.3.3 Совместное влияние гравитационных полей Луны и Солнца на тело Земли
в «соединении» (в новолуние).

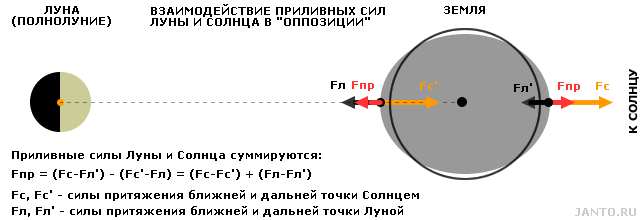
Рис.3.4 Совместное влияние гравитационных полей Луны и Солнца на тело Земли
в «оппозиции» (в полнолуние).

По мере отклонения Луны и Солнца от линии сизигии вызываемые ими приливные силы и, соответственно, приливные волны начинают приобретать самостоятельный характер, их сумма уменьшается, а степень их противодействия друг другу растет. Противодействие достигает максимума, когда угол между направлениями на Луну и Солнце из центра Земли равен 90°, т.е. данные тела находятся в «квадрате», а Луна, соответственно, находится в фазе четверти (первой или последней). В этой конфигурации приливные силы Луны и Солнца действуют на форму тела Земли строго противоположно, соответствующие приливные волны на поверхности максимально разнесены, а их амплитуда минимальна, что иллюстрируется рис. 3.5.

Рис.3.5 Совместное влияние гравитационных полей Луны и Солнца на тело Земли в «квадрате».

Примечание. «Соединение», «оппозиция», «квадрат» (или «квадратура») — термины, используемые в астрономии и астрологии для определения геометрии взаимного расположения двух небесных тел или точек относительно Земли. Подробнее см. Лунные аспекты.

Физика земных приливных процессов под воздействием гравитационных полей Луны и Солнца весьма сложна и требует учета большого числа параметров. На эту тему было разработано большое число различных теорий, проведено много экспериментальных исследований, написано огромное количество статей, монографий и диссертаций. Даже на сегодняшней день в этой области остается много «белых» пятен, противоречащих друг другу точек зрения и альтернативных подходов. Для желающих углубиться в проблематику земных приливов можно рекомендовать фундаментальное исследование П. Мельхиора «Земные приливы» (пер. с англ., М., «Мир», 1968 г. 483 страницы).

3.3. ВЛИЯНИЕ НА ОРБИТУ ЗЕМЛИ

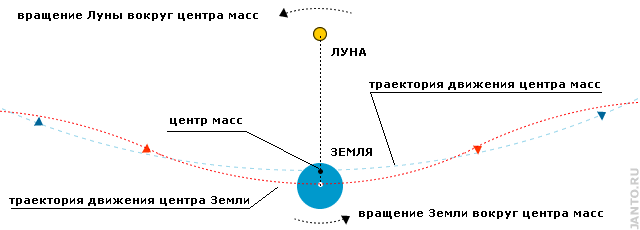
Как было отмечено в п.1.1 главы 1, Луна для естественного спутника планеты обладает аномально большой массой, поэтому более корректно считать, что Земля и Луна образуют двойную планетную систему, вращающуюся вокруг общего центра масс, который смещен относительно центра Земли в среднем на 4670 км. Вследствие этого Земля, вращаясь вокруг своей центральной оси, одновременно вращается и вокруг этого центра масс с периодом, равным синодическому лунному месяцу, т.е. 29,530588 солнечных суток. В результате на эллиптическую орбиту Земли накладывается переменнная «модулирующая» составляющая с соответствующей амплитудой и периодом (см. рис.3.6).

Рис.3.6 Модуляция орбиты Земли лунной гравитацией

Эта составляющая изменяет расстояние от Земли до Солнца, что приводит к колебаниям солнечной гравитации примерно на ± 450 мкгс, практически не влияя на ее градиент. Кроме того, она создает определенные силы инерции, внося дополнительный вклад в изменение силы тяжести в зависимости от положения тела на поверхности Земли, а также незначительно влияет на величину достигающей Земли солнечной энергии (см. здесь).

3.4. КРАТКОЕ РЕЗЮМЕ

Следствием воздействия лунной гравитации на Землю являются два фундаментальных явления:

1. Лунные приливы на поверхности Земли — периодических изменений уровня земной поверхности, синхронизированные с суточным вращением Земли и перемещением Луны по орбите.
2. Наложение на земную орбиту переменной составляющей, синхронизированной с вращением системы Земля — Луна вокруг общего центра масс.

Данные явления являются главными механизмами воздействия Луны на земные сферы — литосферу, гидросферу, земное ядро, атмосферу, магнитосферу и др. Более подробно об этом — в следующей главе.

Видео:Визуализация гравитацииСкачать

Взаимное притяжение Земли и Луны

Что такое притяжение Земли и Луны? Это сила и взаимодействие материи, свойственное всем телам и предметам в нашей Вселенной. По другому, называется гравитацией или всемирным тяготением.

Безусловно, каждый слышал это понятие, но не все понимают его значение и роль в окружающем нас мире. Хотя во многом благодаря силам гравитации этот мир и существует в таком виде, каким мы его наблюдаем вокруг себя. Можно сказать, что земная жизнь напрямую зависит от данного явления.

Гравитация

Видео:Что такое гравитацияСкачать

Сила гравитации на Земле

Гравитационное поле Земли представляет собой поле силы тяжести, которое формируется земным тяготением и центробежной силой планеты, вызванной её вращение вокруг своей оси.

Гравитацию можно рассчитать, если знать массу тел и расстояние между их центрами. Также следует учитывать, гравитационное поле. Поскольку чем оно сильнее, тем больше будет масса тела и, соответственно, его ускорение.

С какой силой притягивается к Земле или точнее, как рассчитать силы гравитации, можно ознакомиться тут.

Видео:Алексей Семихатов — «Общая теория относительности: гравитация и космос»Скачать

Притяжение Земли и Луны

Не секрет, что Луна является естественным спутником нашей планеты. То есть сила притяжения Земли удерживает её возле себя. Однако учёные установили, что расстояние до спутника ежегодно увеличивается почти на 4 см. Почему это происходит, рассмотрим ниже.

Поскольку лунные значения размера и массы меньше нашей планеты, то его сила притяжения намного слабее.

Сила притяжения Луны к Земле

Как стало известно, существует взаимное притяжение Земли и Луны. Разумеется, взаимодействие земной и лунной стороны не проходит незаметно для обоих. По данным учёных, гравитационное поле нашего спутника влияет на разные земные сферы.

Главным образом, лунная гравитация формирует на Земле периодические изменения уровня земной поверхности. Прежде всего, такие изменения связаны с вращением планеты вокруг совей оси и движением Луны по орбите. По-другому их называют лунными приливами.

Земля и Луна

Видео:Как высоко вы могли бы подпрыгнуть на разных планетахСкачать

Что такое лунные приливы и отливы?

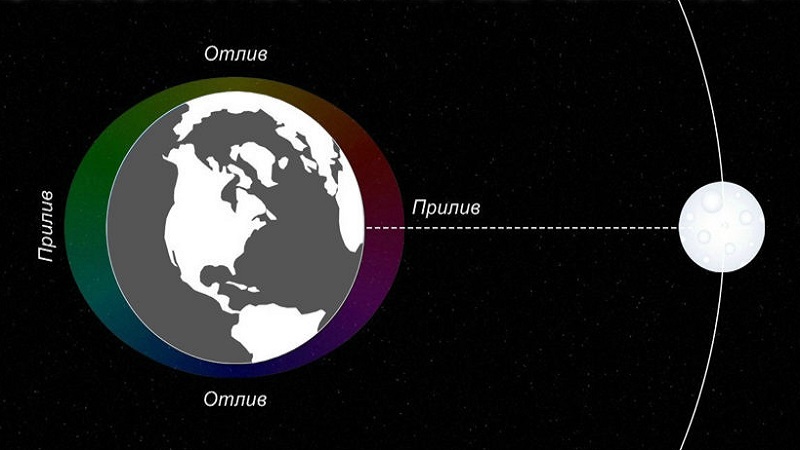
Как оказалось, два раза за сутки происходит повышение и понижение уровня воды на водных просторах Земли. Это связано с притяжением Луной отдельных частиц с земной поверхности. То есть, те элементы, которые находятся ближе к ней, притягиваются сильнее (расстояние между ними уменьшается), и наоборот. А так как наша планета беспрерывно вращается, то и влияние на определенные частицы меняется. Наибольшее влияние оказывается на водную оболочку.

Так вот, сторона, обращенная к Луне в определенный промежуток времени, испытывает большую силу притяжения к ней. В результате вода на этой стороне поднимается, образуя прилив, тем самым снижая уровень воды на противоположной стороне, формируя отлив.

Кроме того, из-за земного вращения приливная волна движется в направлении с запада на восток. А также она опережает лунное движение. В свою очередь, эта борьба на опережение увеличивает скорость движения Луны. Собственно говоря, вот и причина её удаления от Земли.

Лунные приливы и отливы

Однако, перемещение воды в океанах влияет и на саму планету. Поскольку приливная волна практически постоянно наталкивается на материки, что создает для неё препятствия. В итоге, эти преграды, вращение планеты и лунная гравитация вызывают силу, которая действует противоположно земной поверхности.

Как результат, происходит уменьшение скорости вращения Земли вокруг своей оси. Поэтому мы наблюдаем увеличение продолжительности оборота планеты, и соответственно увеличение продолжительности дня. Конечно, процесс данного роста протекает очень медленно. Но его наличие отрицать сложно.

Как видно, любой происходящий процесс на планете, нашей или любой другой, обязательно связан с какими-либо процессами на других объектах. Это могут быть как земные, скажем ближние, объекты, так и космические тела. Все во Вселенной взаимосвязанно и непрерывно. Вероятно, наша задача не просто узнать и изучить взаимодействие, но и использовать накопленные знания для поддержания и сохранения жизни.

Идеальное одиночество и покой — лучшее, что способен подарить людям единственный спутник Земли.

Видео:Про ЛунуСкачать

Моделирование динамических систем: Как движется Луна?

Светлой памяти моего учителя — первого декана физико-математического факультета Новочеркасского политехнического института, заведующего кафедрой «Теоретическая механика» Кабелькова Александра Николаевича

Видео:Почему Луна всегда повёрнута к Земле одной стороной?Скачать

Введение

Август, лето подходит к концу. Народ яростно рванул на моря, да оно и неудивительно — самый сезон. А на Хабре, тем временем, буйным цветом распускается и пахнет лженаука. Если говорить о теме данного выпуска «Моделирования. », то в нем мы совместим приятное с полезным — продолжим обещанный цикл и совсем чуть-чуть поборемся с этой самой лженаукой за пытливые умы современной молодежи.

А вопрос ведь действительной не праздный — со школьных лет мы привыкли считать, что наш ближайший спутник в космическом пространстве — Луна движется вокруг Земли с периодом 29,5 суток, особенно не вдаваясь в сопутствующие подробности. На самом же деле наша соседка своеобразный и в какой-то степени уникальный астрономический объект, с движением которого вокруг Земли не всё так просто, как, возможно хотелось бы некоторым моим коллегам из ближайшего зарубежья.

Итак, оставив полемику в стороне, попытаемся с разных сторон, в меру своей компетенции, рассмотреть эту безусловно красивую, интересную и очень показательную задачу.

Видео:УЧЁНЫЕ НАС ДУРЯТ С РОЖДЕНИЯ. 7 КРАМОЛЬНЫХ ФАКТОВ О ГРАВИТАЦИИ. РАЗОБЛАЧЕНИЕ ЛЖИ НЬЮТОНА И ФИЗИКОВСкачать

1. Закон всемирного тяготения и какие выводы мы можем из него сделать

где m₁, m₂ — массы, соответственно Луны и Земли; G = 6,67e-11 м 3 /(кг * с 2 ) — гравитационная постоянная; r_1,2 — расстояние между центрами Луны и Земли. Если принимать во внимание только эту силу, то, решив задачу о движении Луны как спутника Земли и научившись рассчитывать положение Луны на небе на фоне звезд, мы довольно скоро убедимся, путем прямых измерений экваториальных координат Луны, что в нашей консерватории не всё так гладко как хотелось бы. И дело здесь не в законе всемирного тяготения (а на ранних этапах развития небесной механики такие мысли высказывались весьма нередко), а в неучтенном возмущении движения Луны со стороны других тел. Каких? Смотрим на небо и наш взгляд сразу упирается в здоровенный, массой аж 1,99e30 килограмм плазменный шар прямо у нас под носом — Солнце. Луна притягивается к Солнцу? Ещё как, с силой, равной по модулю

где m₃ — масса Солнца; r_1,3 — расстояние от Луны до Солнца. Сравним эту силу с предыдущей

Возьмем положение тел, в котором притяжение Луны к Солнцу будет минимальным: все три тела на одной прямой и Земля располагается между Луной и Солнцем. В этом случае наша формула примет вид:

где , м — среднее расстояние от Земли до Луны; , м — среднее расстояние от Земли до Солнца. Подставим в эту формулу реальные параметры

Вот это номер! Получается Луна притягивается к Солнцу силой, более чем в два раза превышающей силу её притяжения к Земле.

Подобное возмущение уже нельзя не учитывать и оно определенно повлияет на конечную траекторию движения Луны. Пойдем дальше, принимая во внимание допущение о том, что орбита Земли круговая с радиусом a, найдем геометрическое место точек вокруг Земли, где сила притяжения любого объекта к Земле равна силе его притяжения к Солнцу. Это будет сфера, с радиусом

смещенная вдоль прямой, соединяющей Землю и Солнце в сторону противоположенную направлению на Солнце на расстояние

где — отношение массы Земли к массе Солнца. Подставив численные значения параметров получим фактические размеры данной области: R = 259300 километров, и l = 450 километров. Эта сфера носит название сферы тяготения Земли относительно Солнца.

Известная нам орбита Луны лежит вне этой области. То есть в любой точке траектории Луна испытывает со стороны Солнца существенно большее притяжение, чем со стороны Земли.

Видео:Почему мы НЕ видим обратную сторону Луны? 🌘 #астрономия #космос #планеты #луна #сурдин #звезды #nasaСкачать

2. Спутник или планета? Гравитационная сфера действия

Эта информация, часто порождает споры, о том, что Луна не спутник Земли, а самостоятельная планета Солнечной системы, орбита которой возмущена притяжением близкой Земли.

Оценим возмущение, вносимое Солнцем в траекторию Луны относительно Земли, а так же возмущение, вносимое Землей в траекторию Луны относительно Солнца, воспользовавшись критерием, предложенным П. Лапласом. Рассмотрим три тела: Солнце (S), Землю (E) и Луну (M).
Примем допущение, что орбиты Земли относительно Солнца и Луны относительно Земли являются круговыми.

С другой стороны, в соответствии с теоремой Кориолиса, абсолютное ускорение Луны

где — переносное ускорение, равное ускорению Земли относительно Солнца; — ускорение Луны относительно Земли. Ускорения Кориолиса здесь не будет — выбранная нами система координат движется поступательно. Отсюда получаем ускорение Луны относительно Земли

Часть этого ускорения, равная обусловлена притяжением Луны к Земле и характеризует её невозмущенное геоцентрическое движение. Оставшаяся часть

ускорение Луны, вызванное возмущением со стороны Солнца.

Если рассматривать движение Луны в гелиоцентрической инерциальной системе отсчета, то всё намного проще, ускорение характеризует невозмущенное гелиоцентрическое движение Луны, а ускорение — возмущение этого движения со стороны Земли.

При существующих в текущую эпоху параметрах орбит Земли и Луны, в каждой точке траектории Луны справедливо неравенство

что можно проверить и непосредственным вычислением, но я сошлюсь на источник, дабы излишне не загромождать статью.

Что означает неравенство (1)? Да то, что в относительном выражении эффект от возмущения Луны Солнцем (причем очень существенно) меньше эффекта от притяжения Луны к Земле. И наоборот, возмущение Землей геолиоцентрической траектории Луны оказывает решающее влияние на характер её движения. Влияние земной гравитации в данном случае более существенно, а значит Луна «принадлежит» Земле по праву и является её спутником.

Интересным является другое — превратив неравенство (1) в уравнение можно найти геометрическое место точек, где эффекты возмущения Луны (да и любого другого тела) Землей и Солнцем одинаковы. К сожалению это у же не так просто, как в случае со сферой тяготения. Расчеты показывают, что данная поверхность описывается уравнением сумасшедшего порядка, но близка к эллипсоиду вращения. Всё что мы может сделать без лишних заморочек, это оценить общие габариты этой поверхности относительно центра Земли. Решая численно уравнение

относительно расстояния от центра Земли до искомой поверхности на достаточном количестве точек, получаем сечение искомой поверхности плоскостью эклиптики

Для наглядности здесь показаны и геоцентрическая орбита Луны и, найденная нами выше сфера тяготения Земли относительно Солнца. Из рисунка видно, что сфера влияния, или сфера гравитационного действия Земли относительно Солнца есть поверхность вращения относительно оси X, сплющенная вдоль прямой, соединяющей Землю и Солнце (вдоль оси затмений). Орбита Луны находится глубоко внутри этой воображаемой поверхности.

Для практических расчетов данную поверхность удобно аппроксимировать сферой с центром в центра Земли и радиусом равным

где m — масса меньшего небесного тела; M — масса большего тела, в поле тяготения которого движется меньшее тело; a — расстояние между центрами тел. В нашем случае

Вот этот недоделанный миллион километров и есть тот теоретический предел, за который власть старушки Земли не распространяется — её влияние на траектории астрономических объектов настолько мало, что им можно пренебречь. А значит, запустить Луну по круговой орбите на расстоянии 38,4 млн. километров от Земли (как делают некоторые лингвисты) не получится, это физически невозможно.

Эта сфера, для сравнения, показана на рисунке синей пунктирной линией. При оценочных расчетах принято считать, что тело, находящееся внутри данной сферы будет испытывать тяготение исключительно со стороны Земли. Если тело находится снаружи данной сферы — считаем что тело движется в поле тяготения Солнца. В практической космонавтике известен метод сопряжения конических сечений, позволяющий приближенно рассчитать траекторию космического аппарата, используя решение задачи двух тел. При этом всё пространство, которое преодолевает аппарат разбивается на подобные сферы влияния.

Например, теперь понятно, для того чтобы иметь теоретическую возможность совершить маневры для выхода на окололунную орбиту, космический аппарат должен попасть внутрь сферы действия Луны относительно Земли. Её радиус легко рассчитать по формуле (3) и он равен 66 тысяч километров.

Таким образом, Луна справедливо может считаться спутником Земли. Однако, ввиду существенно влияния гравитационного поля Солнца она движется не в центральном гравитационном поле, а значит её траектория не является коническим сечением.

Видео:Физика онлайн "Человечество смотрит на звезды" лекция 5. АстероидыСкачать

3. Задача трех тел в классической постановке

Итак, рассмотрим модельную задачу в общей постановке, известную в небесной механике как задача трех тел. Рассмотрим три тела произвольной массы, расположенных произвольным образом в пространстве и движущихся исключительно под действием сил взаимного гравитационного притяжения

Тела считаем материальными точками. Положение тел будем отсчитывать в произвольном базисе, с которым связана инерциальная система отсчета Oxyz. Положение каждого из тел задается радиус-вектором соответственно , и . На каждое тело действует сила гравитационного притяжения со стороны двух других тел, причем в соответствии с третьей аксиомой динамики точки (3-й закон Ньютона)

Запишем дифференциальные уравнения движения каждой точки в векторной форме

В соответствии с законом всемирного тяготения, силы взаимодействия направлены вдоль векторов

Вдоль каждого из этих векторов выпустим соответствующий орт

тогда каждая из гравитационных сил рассчитывается по формуле

С учетом всего этого система уравнений движения принимает вид

Введем обозначение, принятое в небесной механике

— гравитационный параметр притягивающего центра. Тогда уравнения движения примут окончательный векторный вид

Видео:ВЛИЯНИЕ ЛУНЫ НА ЗЕМЛЮ | THE SPACEWAYСкачать

4. Нормирование уравнений к безразмерным переменным

Довольно популярным приемом при математическом моделировании является приведение дифференциальных уравнений и прочих соотношений, описывающих процесс, к безразмерным фазовым координатам и безразмерному времени. Нормируются так же и другие параметры. Это позволяет рассматривать, хоть и с применением численного моделирования, но в достаточно общем виде целый класс типовых задач. Вопрос о том, насколько это оправдано в каждой решаемой задаче оставляю открытым, но соглашусь, что в данном случае такой подход вполне справедлив.

Итак, введем некое абстрактное небесное тело с гравитационным параметром , такое, что период обращения спутника по эллиптической орбите с большой полуосью вокруг него равен . Все эти величины, в силу законов механики, связаны соотношением

Введем замену параметров. Для положения точек нашей системы

где — безразмерный радиус-вектор i-й точки;
для гравитационных параметров тел

где — безразмерный гравитационный параметр i-й точки;
для времени

где — безразмерное время.

Теперь пересчитаем ускорения точек системы через эти безразмерные параметры. Применим прямое двукратное дифференцирование по времени. Для скоростей

При подстановке полученных соотношений в уравнения движения всё элегантно схлопывается в красивые уравнения:

Данная система уравнений до сих пор считается не интегрируемой в аналитических функциях. Почему считается а не является? Потому что успехи теории функции комплексного переменного привели к тому, что общее решение задачи трех тел таки появилось в 1912 году — Карлом Зундманом был найден алгоритм отыскания коэффициентов для бесконечных рядов относительно комплексного параметра, теоретически являющихся общим решением задачи трех тел. Но… для применения рядов Зундмана в практических расчетах с требуемой для них точностью требует получения такого числа членов этих рядов, что эта задача во много превосходит возможности вычислительных машин даже на сегодняшний день.

Поэтому численное интегрирование — единственный способ анализа решения уравнения (5)

Видео:🎬 Вращение Луны и Земли. | НАУКА 4.0Скачать

5. Расчет начальных условий: добываем исходные данные

Как я уже писал ранее, прежде чем начинать численное интегрирование, следует озаботится расчетом начальных условий для решаемой задачи. В рассматриваемой задаче поиск начальных условий превращается в самостоятельную подзадачу, так как система (5) дает нам девять скалярных уравнений второго порядка, что при переходе к нормальной форме Коши повышает порядок системы ещё в 2 раза. То есть нам необходимо рассчитать целых 18 параметров — начальные положения и компоненты начальной скорости всех точек системы. Где мы возьмем данные о положении интересующих нас небесных тел? Мы живем в мире, где человек ходил по Луне — естественно человечество должно обладать информацией, как эта самая Луна движется и где она находится.

То есть, скажете вы, ты, чувак, предлагаешь нам взять с полок толстые астрономические справочники, сдуть с них пыль… Не угадали! Я предлагаю сходить за этими данными к тем, кто собственно ходил по Луне, к NASA, а именно в Лабораторию реактивного движения, Пасадена, штат Калифорния. Вот сюда — JPL Horizonts web interface.

Здесь, потратив немного времени на изучение интерфейса, мы добудем все необходимые нам данные. Выберем дату, например, да нам всё равно, но пусть это будет 27 июля 2018 года UT 20:21. Как раз в этот момент наблюдалась полная фаза лунного затмения. Программа выдаст нам огромную портянку

Бр-р-р, что это? Без паники, для того, кто хорошо учил в школе астрономию, механику и математику тут боятся нечего. Итак, самое главное конечное искомые координаты и компоненты скорости Луны.

Да-да-да, они декартовы! Если внимательно прочесть всю портянку, то мы узнаем, что начало этой системы координат совпадает с центром Земли. Плоскость XY лежит в плоскости земной орбиты (плоскости эклиптики) на эпоху J2000. Ось X направлена вдоль линии пересечения плоскости экватора Земли и эклиптики в точку весеннего равноденствия. Ось Z смотрит в направлении северного полюса Земли перпендикулярно плоскости эклиптики. Ну а ось Y дополняет всё это счастье до правой тройки векторов. По-умолчанию единицы измерения координат: астрономические единицы (умнички из NASA приводят и величину автрономической единицы в километрах). Единицы измерения скорости: астрономические единицы в день, день принимается равным 86400 секундам. Полный фарш!

Аналогичную информацию мы можем получить и для Земли

Здесь в качестве начала координат выбран барицентр (центр масс) Солнечной системы. Интересующие нас данные

Для Луны нам понадобятся координаты и скорость относительно барицентра Солнечной системы, мы можем их посчитать, а можем попросит NASA дать нам такие данные

Чудесно! Теперь необходимо слегка обработать полученные данные напильником.

Видео:Расчёт силы притяжения между Землёй и ЛунойСкачать

6. 38 попугаев и одно попугайское крылышко

Для начала определимся с масштабом, ведь наши уравнения движения (5) записаны в безразмерной форме. Данные, предоставленные NASA сами подсказывают нам, что за масштаб координат стоит взять одну астрономическую единицу. Соответственно в качестве эталонного тела, к которому мы будем нормировать массы других тел мы возьмем Солнце, а в качестве масштаба времени — период обращения Земли вокруг Солнца.

Все это конечно очень хорошо, но мы не задали начальные условия для Солнца. «Зачем?» — спросил бы меня какой-нибудь лингвист. А я бы ответил, что Солнце отнюдь не неподвижно, а тоже вращается по своей орбите вокруг центра масс Солнечной системы. В этом можно убедится, взглянув на данные NASA для Солнца

Взглянув на параметр RG мы увидим, что Солнце вращается вокруг барицентра Солнечной системы, и на 27.07.2018 центр звезды находится от него на расстоянии в миллион километров. Радиус Солнца, для справки — 696 тысяч километров. То есть барицентр Солнечной системы лежит в полумиллионе километров от поверхности светила. Почему? Да потому что все остальные тела, взаимодействующие с Солнцем так же сообщают ему ускорение, главным образом, конечно тяжеленький Юпитер. Соответственно у Солнца тоже есть своя орбита.

Мы конечно можем выбрать эти данные в качестве начальных условий, но нет — мы же решаем модельную задачу трех тел, и Юпитер и прочие персонажи в неё не входят. Так что в ущерб реализму, зная положение и скорости Земли и Луны мы пересчитаем начальные условия для Солнца, так, чтобы центр масс системы Солнце — Земля — Луна находился в начале координат. Для центра масс нашей механической системы справедливо уравнение

Поместим центр масс в начало координат, то есть зададимся , тогда

Перейдем к безразмерным координатам и параметрам, выбрав

Дифференцируя (6) по времени и переходя к безразмерному времени получаем и соотношение для скоростей

где

Теперь напишем программу, которая сформирует начальные условия в выбранных нами «попугаях». На чем будем писать? Конечно же на Питоне! Ведь, как известно, это самый лучший язык для математического моделирования.

Однако, если уйти от сарказма, то мы действительно попробуем для этой цели питон, а почему нет? Я обязательно приведу ссылку на весь код в моем профиле Github.

Видео:Эксперимент GRAIL — как измерили гравитацию Луны? 🌓 #астрономия #космос #луна #сурдин #планеты #nasaСкачать

7. Интегрирование уравнений движения и анализ результатов

Тогда введя вектор состояния системы

сводим (7) и (5) к одному векторному уравнению

Для интегрирования (8) с имеющимися начальными условиями напишем немного, совсем немного кода

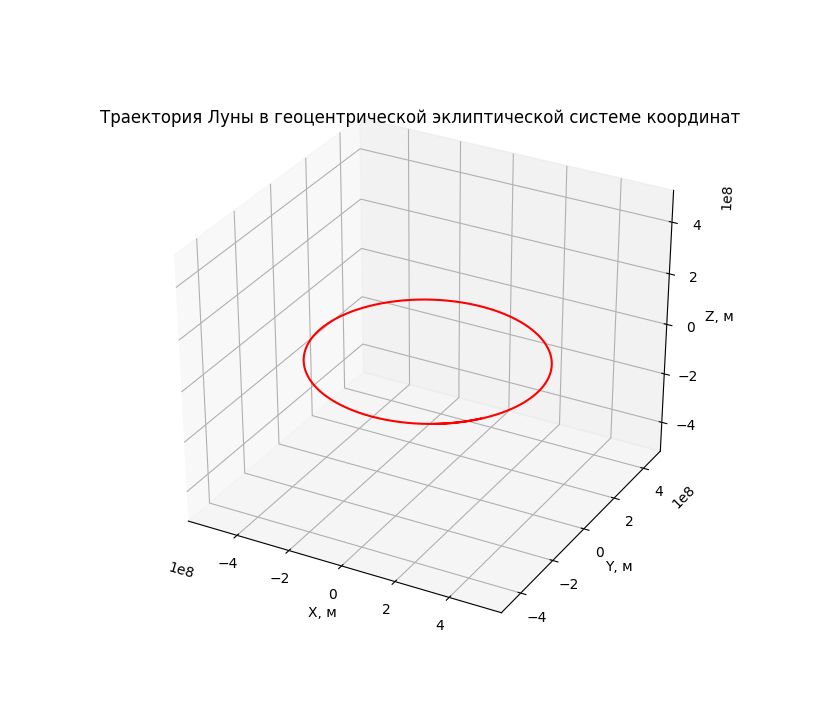
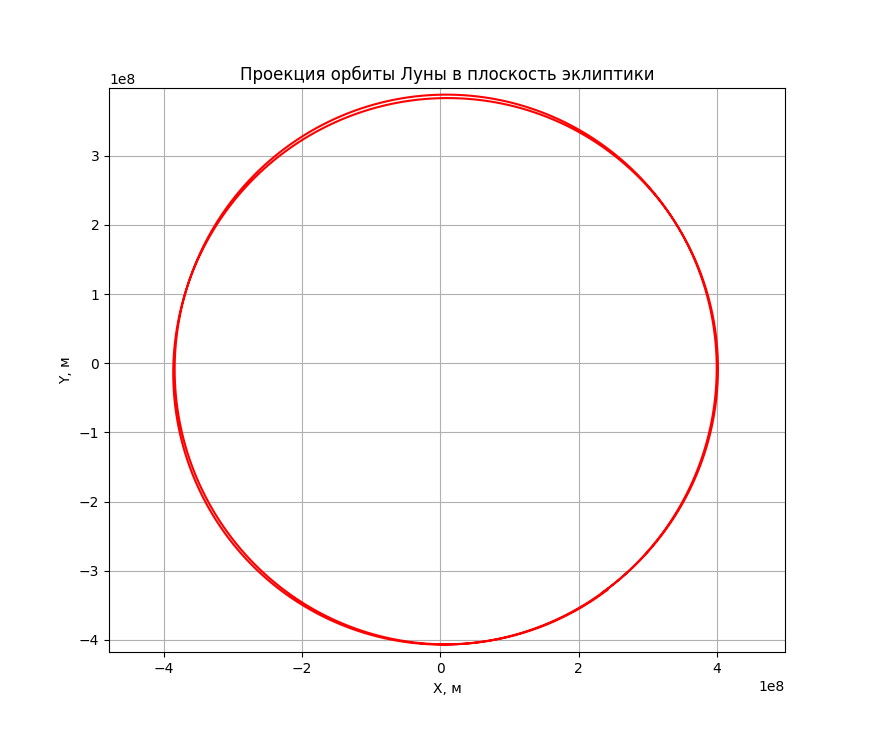
Посмотрим что у нас получилось. Получилась пространственная траектория Луны на первые 29 суток от выбранной нами начальной точки

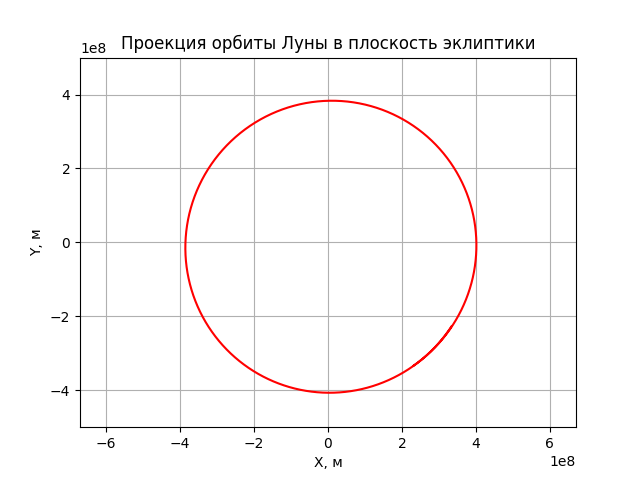
а так же её проекция в плоскость эклиптики.

«Эй, дядя, что ты нам впариваешь?! Это же окружность!».

Во-первых, таки не окружность — заметно смещение проекции траектории от начала координат вправо и вниз. Во-вторых — ничего не замечаете? Не, ну правда?

Обещаю подготовить обоснование того (на основе анализа погрешностей счета и данных NASA), что полученное смещение траектории не есть следствие ошибок интегрирования. Пока предлагаю читателю поверить мне на слово — это смещение есть следствие солнечного возмущения лунной траектории. Крутанем-ка еще один оборот

Во как! Причем обратите внимание на то, что исходя из начальных данных задачи Солнце находится как раз в той стороне, куда смещается траектория Луны на каждом обороте. Да это наглое Солнце ворует у нас наш любимый спутник! Ох уж это Солнце!

Можно сделать вывод, что солнечная гравитация влияет на орбиту Луны достаточно существенно — старушка не ходит по небу дважды одним и тем же путём. Картинка за полгода движения позволяет (по крайней мере качественно) убедится в этом (картинка кликабельна)

Интересно? Ещё бы. Астрономия вообще наука занятная.

Видео:Что будет с океанскими приливами, когда Луна удалится от Земли?Скачать

Постскриптум

В вузе, где я учился и работал без малого семь лет — Новочеркасском политехе — ежегодно проводилась зональная олимпиада студентов по теоретической механике вузов Северного Кавказа. Трижды мы принимали и Всероссийскую олимпиаду. На открытии, наш главный «олимпиец», профессор Кондратенко А.И., всегда говорил: «Академик Крылов называл механику поэзией точных наук».

Я люблю механику. Всё то хорошее, чего я добился в своей жизни и карьере произошло благодаря этой науке и моим замечательным учителям. Я уважаю механику.

Поэтому, я никогда не позволю издеваться над этой наукой и нагло эксплуатировать её в своих целях никому, будь он хоть трижды доктор наук и четырежды лингвист, и разработал хоть миллион учебных программ. Я искренне считаю, что написание статей на популярном публичном ресурсе должно предусматривать их тщательную вычитку, нормальное оформление (формулы LaTeX — это не блажь разработчиков ресурса!) и отсутствие ошибок, приводящих к результатам нарушающим законы природы. Последнее вообще «маст хэв».

Я часто говорю своим студентам: «компьютер освобождает ваши руки, но это не значит, что при этом нужно отключать и мозг».

Ценить и уважать механику я призываю и вас, мои уважаемые читатели. Охотно отвечу на любые вопросы, а исходный текст примера решения задачи трех тел на языке Python, как и обещал, выкладываю в своем профиле Github.

📹 Видео

Лунная гравитация на земле | CRASH ZONE | Moon Gravity on EarthСкачать

Что произойдет, если Луна врежется в ЗемлюСкачать

Луна и ее влияние на ЗемлюСкачать

Странный объект на орбите: у Земли есть вторая луна?Скачать

Луна не вращается вокруг Земли!Скачать