Уравнение грани пирамиды по вершинам (2 видео)

Онлайн решение Пирамиды по координатам вершин

1) чертёж пирамиды по координатам её вершин;

2) длины и уравнения рёбер, медиан, апофем, высот;

3) площади и уравнения граней;

4) система линейных неравенств, определяющих пирамиду;

5) основания и точка пересечения медиан (центроид);

6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;

7) объём пирамиды;

8) основания, площади и уравнения биссекторов;

9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;

10) параметры и уравнения вписанной и описанной сфер;

Внимание! Этот сервис может не работать в браузере Internet Explorer.

Запишите координаты вершин пирамиды и нажмите кнопку.

A ( ; ; ), B ( ; ; ),
C ( ; ; ), D ( ; ; )

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Содержание

Примеры решений по аналитической геометрии в пространстве
Решения задачи о пирамиде онлайн
Как рассчитать объем пирамиды по координатам вершин? Методика и пример задачи
Что представляет собой пирамида?
Как рассчитывается объем пирамиды?
Как найти объем пирамиды по координатам вершин: методика
Задача с треугольной пирамидой
🎦 Видео

Видео:Математика без Ху!ни. Смешанное произведение векторовСкачать

Примеры решений по аналитической геометрии в пространстве

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии в пространстве, которые относятся к исследованию пирамиды. Обычно в такой задаче нужно найти длины ребер, углы между ребрами, уравнения граней пирамиды и их площади, объем пирамиды, угол между ребром и гранью, уравнение высоты, длину высоты пирамиды и т.д.

Видео:Даны вершины пирамиды A, B, C, D. Найдите объём пирамиды и высоту, опущенную на грань ACDСкачать

Решения задачи о пирамиде онлайн

Задача 1. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.

Задача 2. Даны координаты вершин пирамиды $$A(12;11;17), B(14;12;14), C(13;14;15), D(12;21;12).$$ Найти:
— объем пирамиды;
— площадь грани $ABC$;
— уравнение плоскости, проходящей через точки $B,C,D$;
— длину высоты пирамиды, опущенной на грань $ABC$.

Задача 3. Пирамида $АВСD$ задана координатами своих вершин: $$А(4, -1,0), B(2, 3, 4), C(-1, 4, 1), D(4, -3, 5).$$ Найдите:
1. угол между ребрами $АВ$ и $АС$,
2. уравнение ребра $АВ$,
3. уравнение грани $АВС$,
4. уравнение высоты, опущенной из вершины $D$, на грань $АВС$,
5. выясните, образуют ли векторы $АВ, АС, АD$ линейно независимую систему,
6. координаты вектора $MN$, если $М$ – середина ребра $AD$, $N$ – середина ребра $ВC$,
7. разложите вектор $MN$ по базису $AB, AC, AD$, если он таковым является.

Видео:Уравнения стороны треугольника и медианыСкачать

Как рассчитать объем пирамиды по координатам вершин? Методика и пример задачи

Часто в задачах школьного курса геометрии приходится решать задания, которые требуют использования комплексного подхода. Одной из таких задач является вычисление объема пирамиды по координатам вершин. Как решить эту геометрическую задачу — ответит приведенная ниже статья.

Видео:Задача 6. Вычислить объём тетраэдра с вершинами в точках и его высоту, опущенную из вершины на граньСкачать

Что представляет собой пирамида?

Говоря простыми словами, под этой фигурой понимают пространственный объект, ограниченный треугольными сторонами и одной многоугольной гранью, которая называется основанием. Многоугольное основание может быть произвольным n-угольником на плоскости, например, правильным треугольником, параллелограммом и так далее.

Вам будет интересно: Какую роль играет репродуктивная клетка животных и растений?

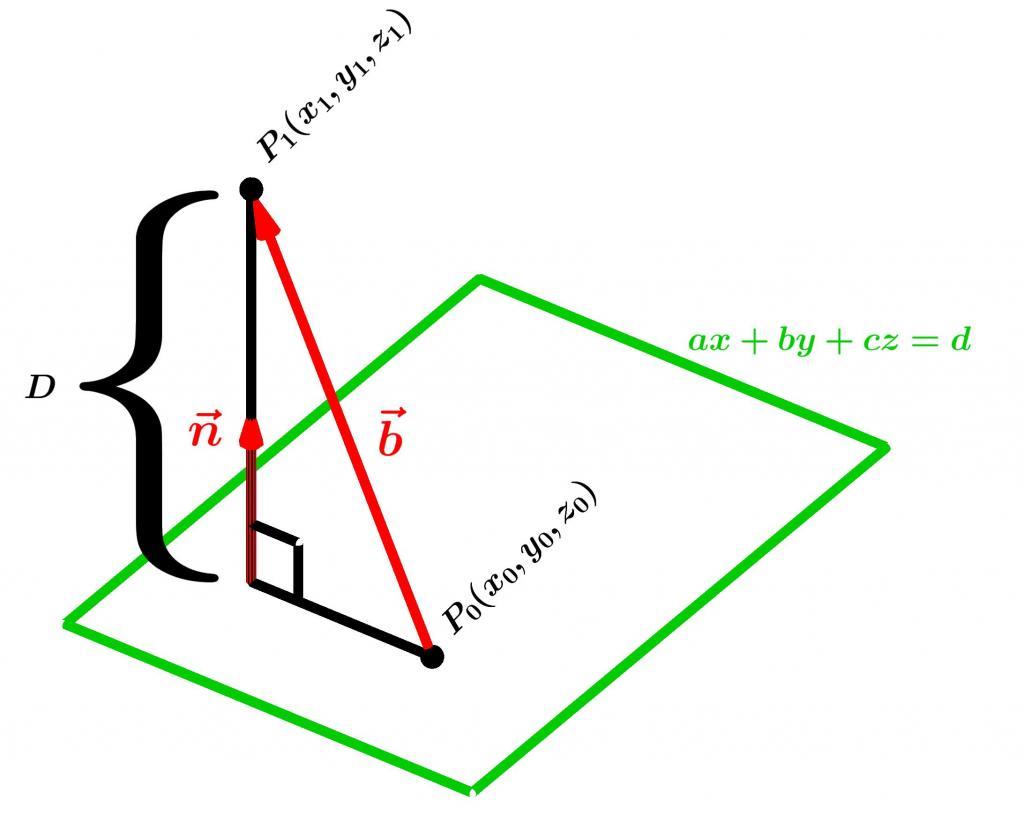
Любая пирамида имеет n + 1 грань, 2 * n ребер и n + 1 вершину. Вершины фигуры не являются равноправными. Так, существует единственная вершина, которая не принадлежит основанию. Она называется главной. Расстояние от нее до плоскости основания — это высота фигуры.

Пирамиды могут быть наклонными, если высота пересекает основание не в его центре, или прямыми, когда высота с основанием пересекается в геометрическом центре последнего. Также фигуры могут быть неправильными и правильными. Пирамиды правильные состоят из равноугольного и равностороннего основания и нескольких равнобедренных треугольников, которые друг другу равны.

Видео:Решение пирамидыСкачать

Как рассчитывается объем пирамиды?

Прежде чем приводить методику вычисления по координатам вершин объема пирамиды, следует привести формулу, при помощи которой можно рассчитать эту величину для фигуры любого типа из рассматриваемого класса. Итак, объем пирамиды рассчитывается так:

Здесь So — это основания площадь, h — расстояние от главной вершины до основания, то есть высота пирамиды.

Таким образом, любая геометрическая задача на нахождение объема пирамиды сводится к расчету величин So и h.

Видео:№973. Даны координаты вершин треугольника ABC: А (4; 6), В (-4; 0), С (-1; -4). Напишите уравнениеСкачать

Как найти объем пирамиды по координатам вершин: методика

Пирамида может быть представлена произвольным n-угольным основанием. Чтобы рассчитать его площадь, следует внимательно изучить условие задачи, в котором должно быть сказано, о каком типе n-угольника идет речь. Если это треугольник или параллелограмм, то расчет его площади по известным координатам очень прост: необходимо лишь найти векторное произведение соответствующих векторов сторон.

Вычислить высоту пирамиды также не представляет особого труда. Для этого следует из любых трех точек основания получить уравнение плоскости в общем виде, а затем нужно воспользоваться формулой расстояния между плоскостью и точкой (вершиной пирамиды). Формула имеет вид:

d = |(A * x1 + B * y1 + C * z1 + D)| / √(A2 + B2 + C2).

Здесь (x1; y1; z1) — координаты точки.

Уравнение плоскости имеет вид:

A * x + B * y + C * z + D = 0.

Видео:Вычисляем высоту через координаты вершин 1Скачать

Задача с треугольной пирамидой

Решим задачу на примере самой простой пирамиды — треугольной. Условие простое: ниже даны координаты вершин пирамиды, объем найти нужно для фигуры, которая на этих координатах построена:

Положим, что основание пирамиды является треугольником ABC. Найдем длины векторов AB¯ и AC¯:

Векторное произведение AB¯ и AC¯ даст нам, с одной стороны, двойную площадь треугольника, то есть 2 * So, а с другой стороны, мы получим координаты нормального к плоскости вектора n¯, имеем:

n¯ = [AB¯ * AC¯] = (8; -10; -7).

Площадь треугольного основания равна полудлине вектора n¯, то есть:

So = √(82 + 102 + 72) / 2 = 7,3.

Прежде чем рассчитывать расстояние от D до плоскости ABC, необходимо записать уравнение плоскости. Три его коэффициента (A, B, C) мы уже знаем, они соответствуют координатам нормали n¯. Свободный член можно получить, подставив в уравнение координаты любой точки плоскости, например точки A, имеем:

D = -1 * (A * x1 + B * y1 + C * z1) = -1 * (8 * 1 + (-10) * 0 + (-7) * 3) = 13.

Тогда уравнение плоскости основания пирамиды принимает форму:

8 * x — 10 * y — 7 * z + 13 = 0.

Теперь применяем приведенную выше формулу для расчета расстояния от точки D(4; 3; 4) до найденной плоскости, получаем:

d = |(8 * 4 — 10 * 3 — 7 * 4 + 13)| / √(82 + 102 + 72) = 0,89.

Поскольку найденное значение расстояния d соответствует высоте пирамиды треугольной h, то можно воспользоваться формулой для объема фигуры:

V = 1 / 3 * So * h = 1 / 3 * 7,3 * 0,89 ≈ 2,166.

Полученное значение объема выражено в кубических единицах выбранной координатной системы.