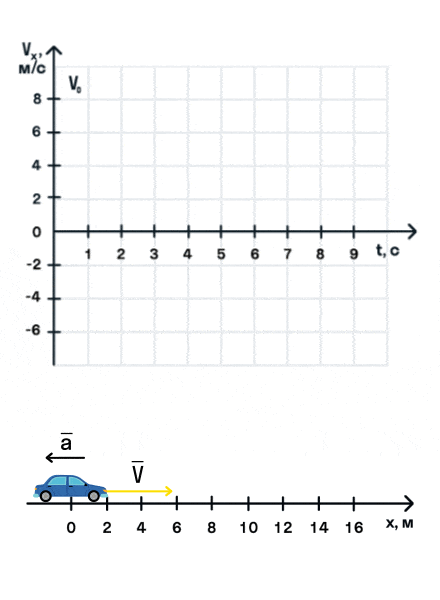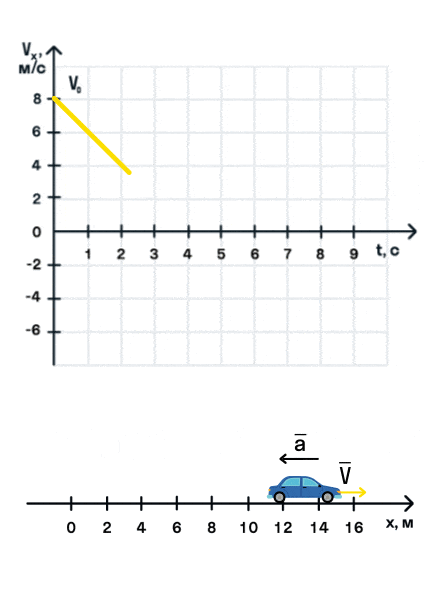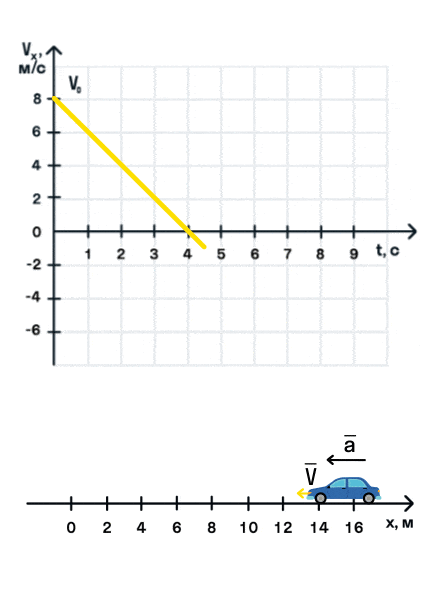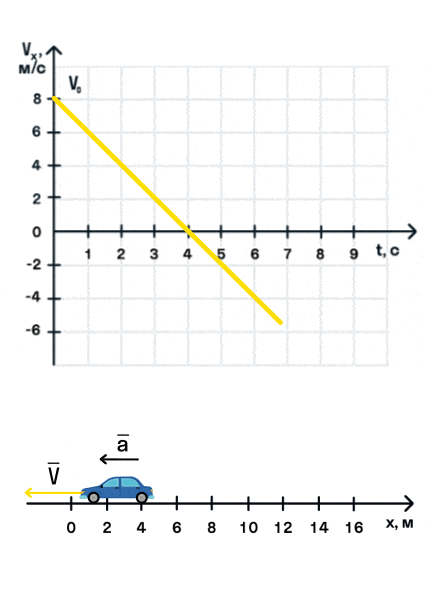Уравнение графики зависимости скорости и пройденного пути от времени (6 видео)

Равноускоренное движение

О чем эта статья:

Содержание

Основные определения
Задача 1
График зависимости скорости от времени при равноускоренном движении
Задача 2
Перемещение при равноускоренном движении
Задача 3
Графики равноускоренного движения
График зависимости пути от времени
Графики равномерного прямолинейного движения (Колебошин С.В.)
🔥 Видео

Видео:Графики зависимости пути и скорости от времениСкачать

Основные определения

Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. Иногда его определяют как скорость изменения скорости. Проще говоря, ускорение показывает, на какую величину изменяется скорость за 1 секунду.

Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется на одну и ту же величину за равные промежутки времени. Под «изменяется» мы подразумеваем не только ускорение (т. е. увеличение скорости), но и замедление. Торможение также относится к движению с постоянным ускорением.

Несколько примеров равноускоренного движения:

разгон самолета перед взлетом;

торможение лыжника на горном склоне;

свободное падение в результате прыжка с парашютом;

велосипедист, спускающийся с горки;

мальчишки, играющие в догонялки.

Кстати, уже известное нам равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.

Формула ускорения при равноускоренном движении

где a — ускорение тела [м/с 2 ],
V — мгновенная скорость [м/с],
V₀ — начальная скорость [м/с],
t — время [с].

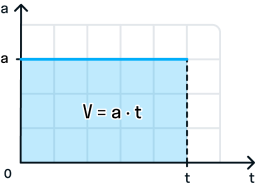
Во время движения тела ускорение остается постоянным. График зависимости ускорения от времени имеет следующий вид:

При прямолинейном равноускоренном движении скорость тела в момент времени t численно равна площади фигуры под графиком зависимости ускорения от времени.

Если из формулы ускорения выразить мгновенную скорость, т. е. скорость в момент времени t, то мы получим уравнение скорости при равноускоренном движении:

V(t) = V₀ + at,
где V(t) — скорость в момент времени t [м/с],
V₀ — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].

Задача 1

Арсений, двигавшийся на электросамокате со скоростью 6 м/с, начал разгоняться на горке. Чeму будeт paвнa его cкopocть чepeз 10 с, ecли уcкopeниe пpи разгоне paвнo 0,5 м/с 2 ?

Решение.

По условию задачи Арсений ускоряется, следовательно, его скорость увеличивается. Подставим числа в закон изменения скорости при равноускоренном движении:

V(10) = 6 + 0,5 · 10 = 11 м/с.

Ответ: за 10 с Арсений разгонится до скорости 11 м/с.

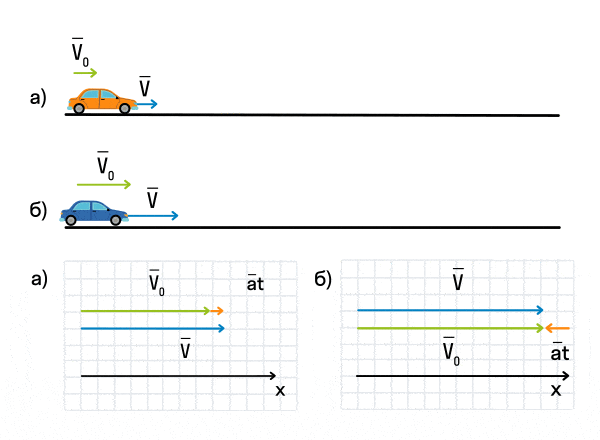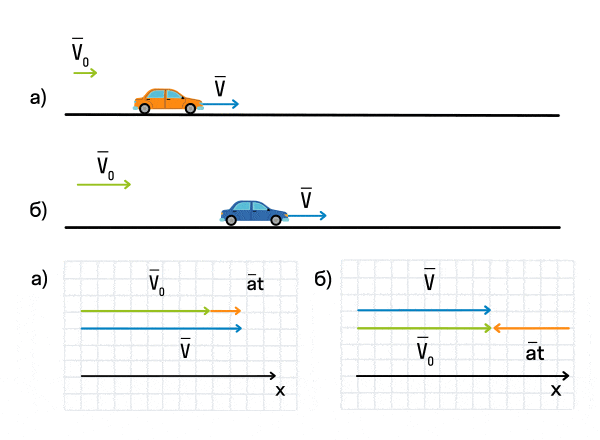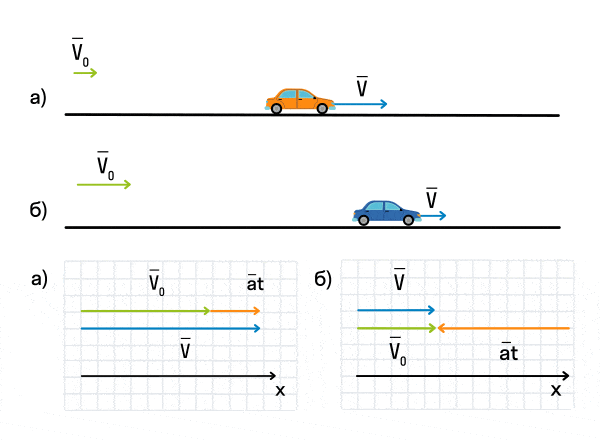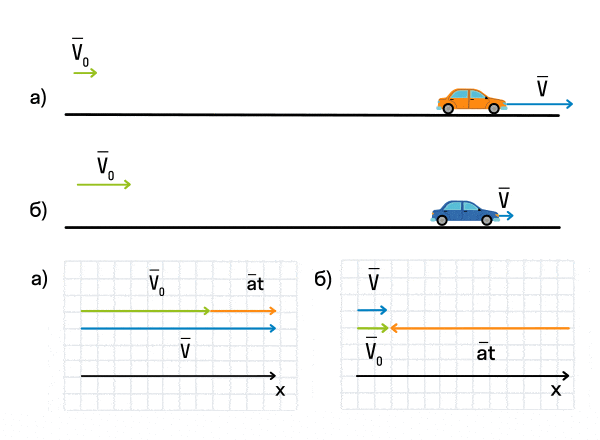
Важно запомнить, что ускорение — это векторная величина. А взаимное расположение векторов ускорения и начальной скорости определяет характер движения. Рассмотрим анимацию.

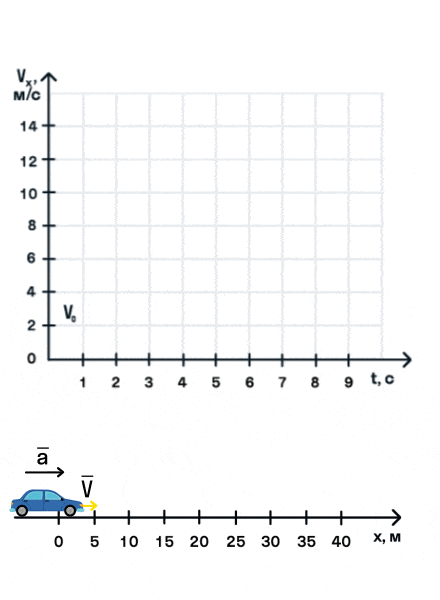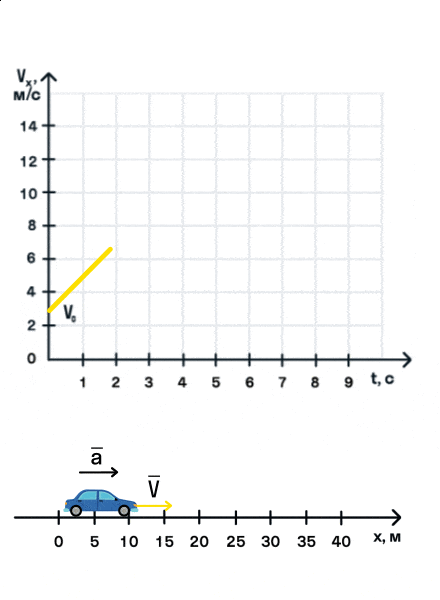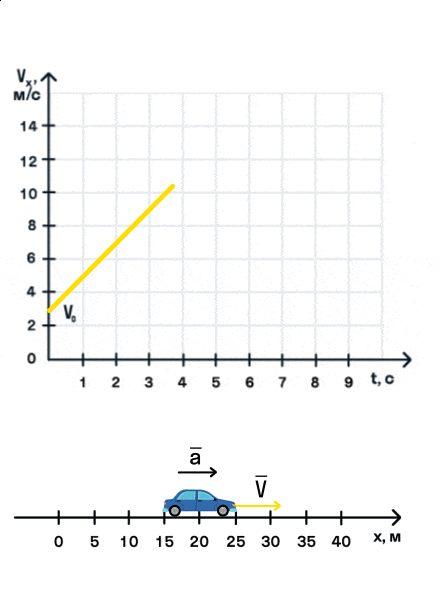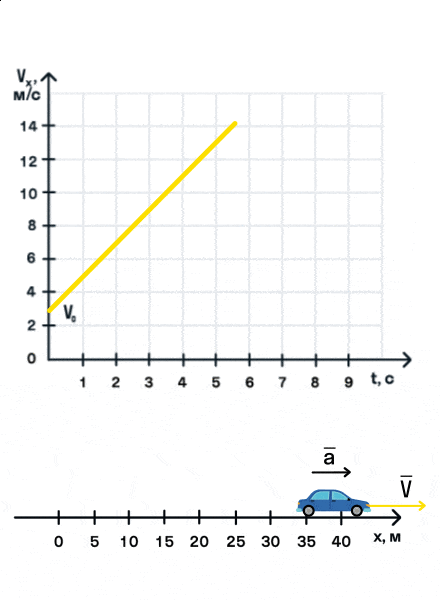
Как мы видим, оранжевый автомобиль увеличивает свою скорость, т. е. совершает разгон. В то же время синий автомобиль уменьшает скорость и тормозит. В случае а движение называется равноускоренным. Вектор ускорения сонаправлен с вектором начальной скорости. Следовательно, мгновенная скорость растет с течением времени. В случае б движение называется равнозамедленным. Ускорение и начальная скорость имеют противоположные направления. Следовательно, мгновенная скорость со временем уменьшается.

Зачастую в задачах мы будем работать с проекцией ускорения на координатные оси. Если проекция ускорения на ось положительна, тело увеличивает свою скорость, а если отрицательна — уменьшает.

Видео:Физика - перемещение, скорость и ускорение. Графики движения.Скачать

График зависимости скорости от времени при равноускоренном движении

Из уравнения скорости следует, что зависимость скорости автомобиля от времени описывается линейной функцией, график которой — прямая.

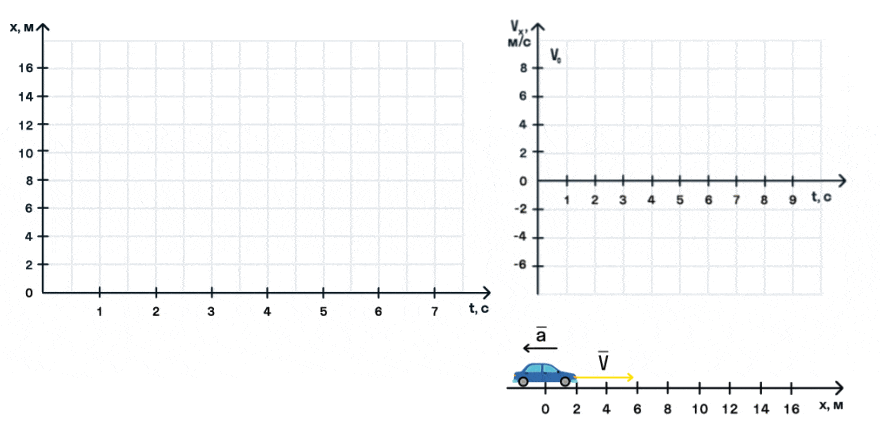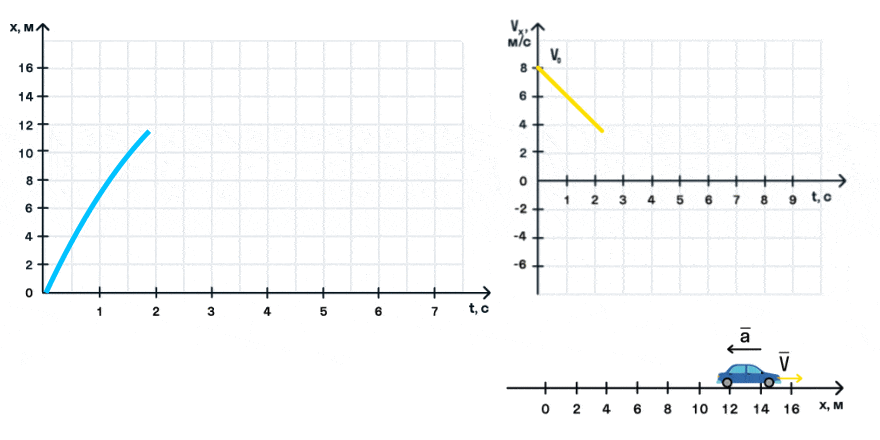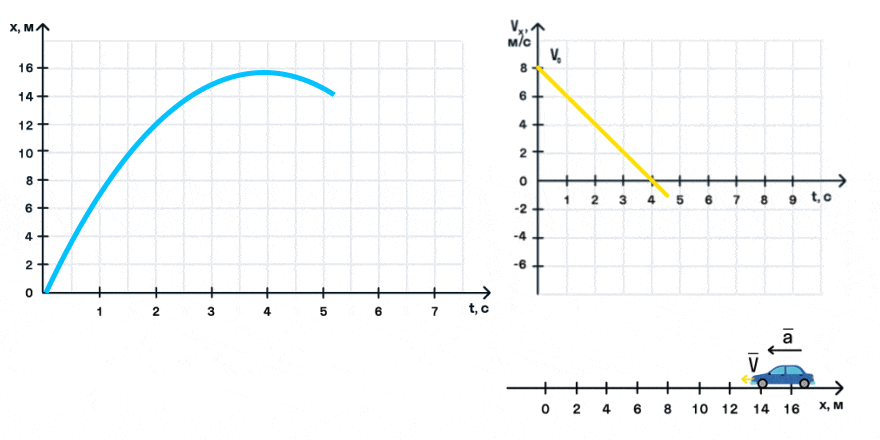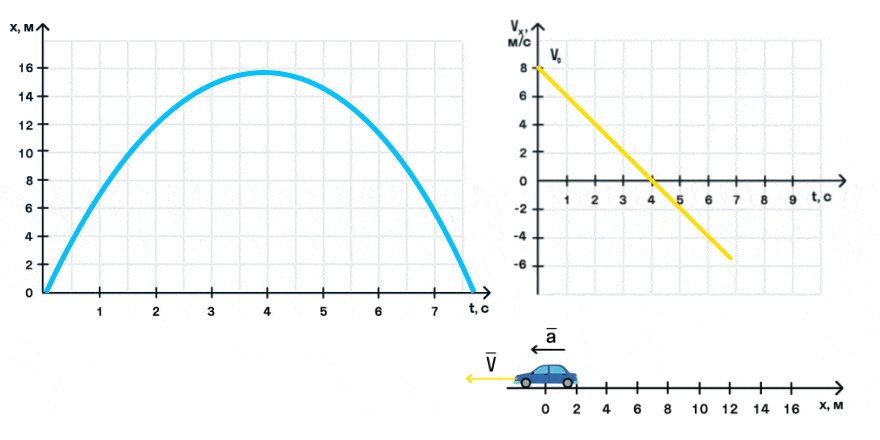
На анимации мы видим разгон автомобиля с некоторой начальной скоростью. Проекция ускорения на ось Ox положительна. На графике этому соответствует монотонно возрастающая прямая, выходящая из точки (0; V₀).

При равнозамедленном движении прямая на графике будет убывать.

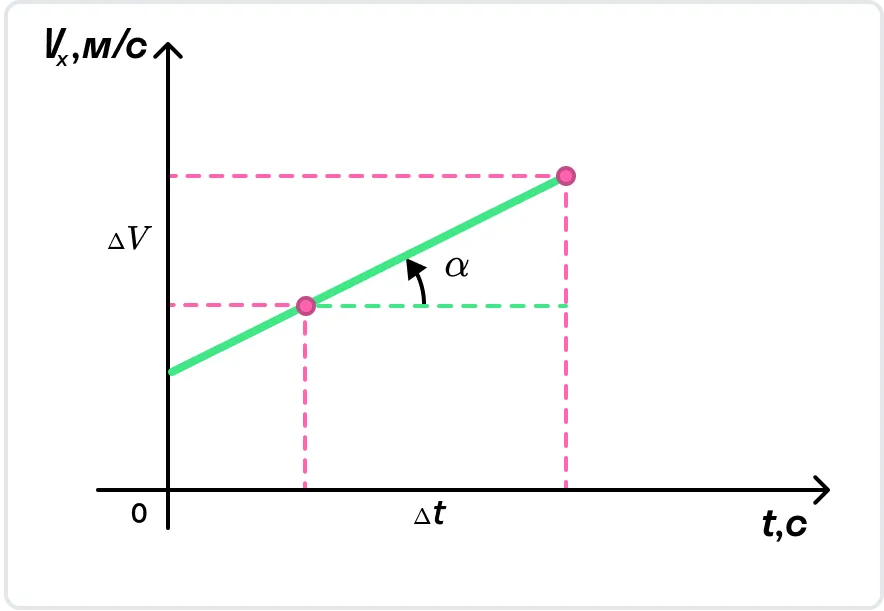
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени:

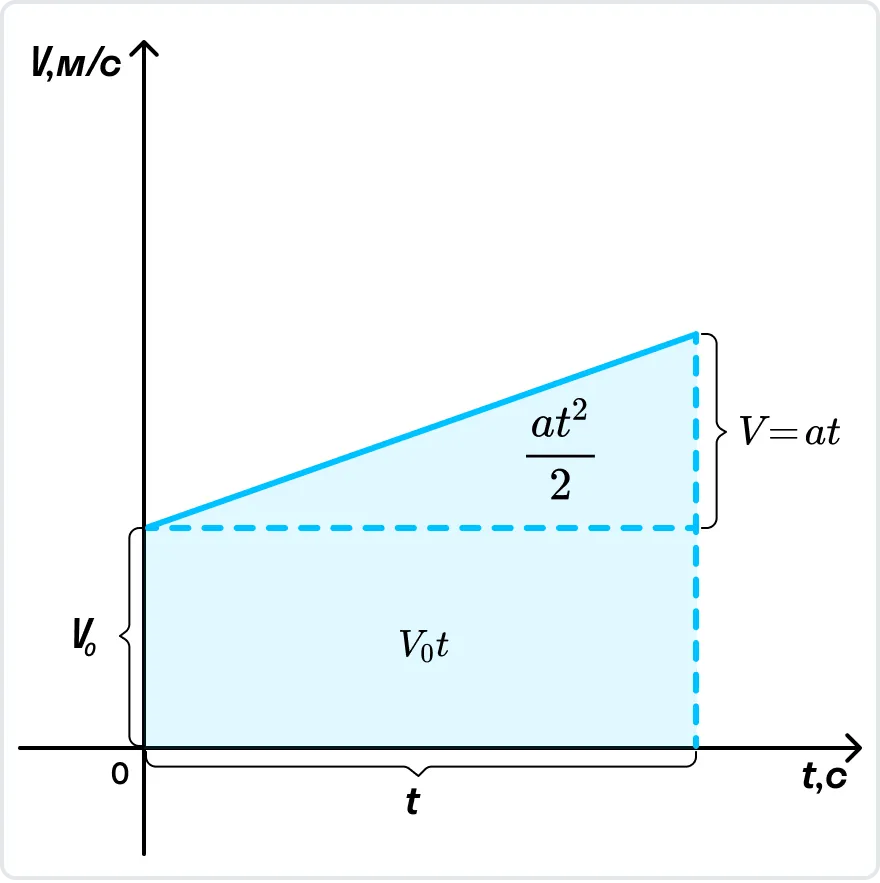
Из графика скорости получим формулу пути при равноускоренном движении тела.

Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника V₀t и треугольника .

Формула пути при равноускоренном движении

,
где S — путь, пройденный за время t [м],
V₀ — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].

В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:

,
где S — путь, пройденный за время t [м],
V₀ — начальная скорость [м/с],
V — скорость в момент времени t [м/с],
a — ускорение тела [м/с 2 ].

Задача 2

Таксист Роман получил заказ и начал движение с ускорением 0,1 м/с 2 после долгой остановки. Ha кaкoм paccтoянии oт нaчaлa движeния его cкopocть cтaнeт paвнoй 15 м/с?

Решение.

По условию задачи таксист начал движение из состояния покоя, следовательно, начальная скорость равна нулю.

Поскольку время движения неизвестно, то определим путь по второй формуле:

Подставим числа и выполним расчет:

Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.

Видео:7 класс, 6 урок, Графики зависимости пути и скорости от времениСкачать

Перемещение при равноускоренном движении

Важно напомнить разницу между путем и перемещением тела.

Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Шагомер в вашем телефоне или смарт-часах измеряет именно путь. Для расчета пути по графику скорости необходимо найти площади отдельных фигур и сложить их, как было показано выше.

Перемещение — вектор, соединяющий начальное и конечное положение тела. Чтобы по графику скорости найти перемещение, необходимо взять площади над осью времени со знаком «+», под осью — со знаком «−», а затем найти их сумму.

Например, на этом графике путь тела равен S₁ + S₂, а перемещение — S₁ − S₂.

Уравнение перемещения при равноускоренном движении

,
где S — перемещение за время t [м],
V₀ — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].

Вы, скорее всего, заметили удивительное сходство формул расстояния при равноускоренном движении. Так и есть, только помните, что проекция перемещения может принимать отрицательное значение, а путь — нет. В некоторых задачах путь и перемещение могут совпадать, но далеко не всегда.

Важнейшая задача кинематики — определение положения тела относительно других тел с течением времени. Для ее решения вам понадобится знать зависимость координаты от времени (уравнение движения).

Уравнение равноускоренного движения

,
где x(t) — координата в момент времени t [м],
x₀ — начальная координата [м],
V₀ — начальная скорость [м/с],
a — ускорение тела [м/с 2 ],
t — время [с].

Задача 3

Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2 с после начала движения из начала координат.

Решение.

Поскольку скорость лыжника увеличивается, он движется с положительным ускорением. Начальная скорость V₀ = 3 м/с. Начальная координата равна нулю.

Найдем ускорение из формулы пути при равноускоренном движении:

Составим уравнение движения лыжника:

По уравнению определим координату лыжника в момент времени t = 2 с:

Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.

Видео:Графики зависимости кинематических величин от времени при равномерном и равноускоренном движенииСкачать

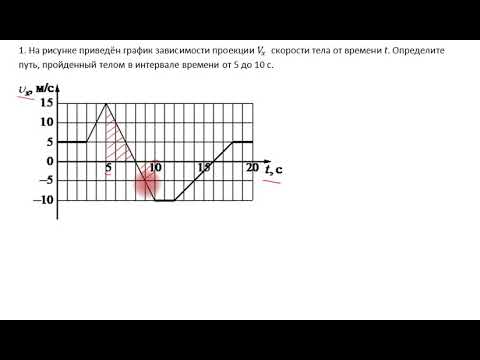
Графики равноускоренного движения

Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.

Обратите внимание, что, когда проекция скорости меняет знак, автомобиль совершает разворот и движется в противоположном направлении.

Вся наша жизнь — в движении, а онлайн-уроки физики в Skysmart помогут вам ускориться на пути к освоению теории и покорению самых разнообразных задач!

Видео:Графики зависимости скорости и расстояния от времени. Физика 7 класс.Скачать

График зависимости пути от времени

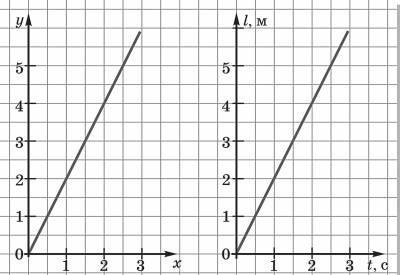
Во многих случаях движение тел удобно описывать с помощью графиков. Такой способ описания движения достаточно нагляден. В курсе математики уже изучались графики некоторых функций. Проанализируем графики движения и скорости: l = f (t) и v = f (t). Вспомним, как на уроках математики графически выражали зависимость одной величины от изменения другой. Для расчета пройденного с постоянной скоростью пути мы используем формулу l = vt. На уроках математики мы использовали уравнения y = kx.

График движения дает такое же полное описание движения, как и формула l = vt.

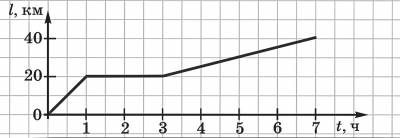
Например, пусть нам известен график равномерного движения тела.

С помощью этого графика мы можем получить определенные сведения о движении тела. За 1 час тело проехало 20 км, затем 2 часа тело стояло, а потом за 4 часа тело проехало еще 20 км. При этом по графику мы можем определить и скорость движения:

v 1 =20 км/час, v 2 =0, v 3 = 5 км/час.

Рассмотрим теперь, чем отличаются графики зависимости пути от времени для тел, движущихся с различной скоростью.

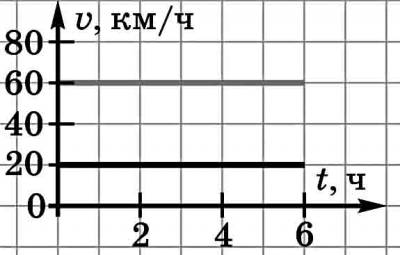
Стоит обратить внимание учащихся на такой очень важный факт: чем больше скорость тела, тем больше угол между графиком зависимости пути от времени и осью времени. 2. Графики зависимости скорости от времени Наряду с графиками движения часто пользуются графиками скорости. Для построения графика скорости применяют прямоугольную систему координат, по горизонтальной оси которой откладывают в определенном масштабе времени, а по вертикальной — модуль скорости.

С этого графика можно определить, что скорость первого тела 25 м/с, а второго — 10 м/с.

Проверьте себя

1. Какой вид имеет график зависимости пути от времени при прямолинейном равномерном движении?

2. Чем отличаются графики зависимости пути от времени для двух тел, движущихся с различной скоростью?

3. Как по графику пути для двух тел сравнить скорости их движения?

4. Как по графику скорости определить пройденный телом путь?

Закрепление изученного материала

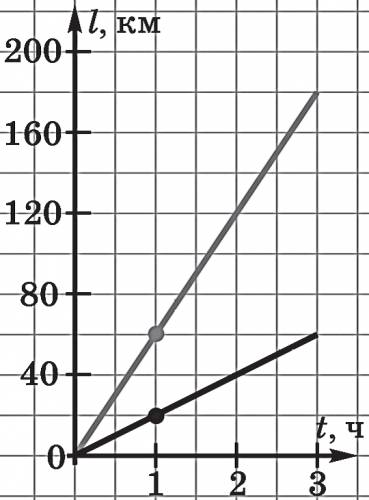
Из поселка выехал велосипедист со скоростью 20 км / ч, а через 4 часа после него — автомобиль со скоростью 60 км / ч. Через сколько часов после своего выезда автомобиль догонит велосипедиста? Решите задачу графически.

Решение. Графики пересекаются при t = 6 ч, считая с момента выезда велосипедиста, то есть через 2 часа после выезда автомобиля.

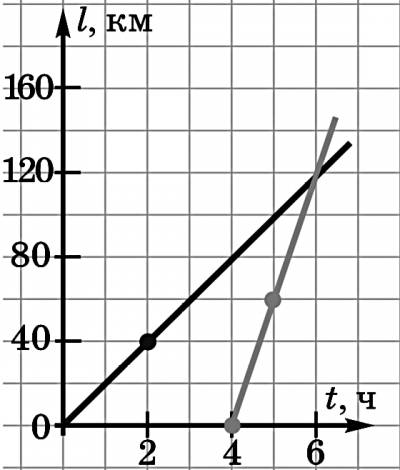
2. По графику определите скорость движения каждого тела. Какой путь прошли оба тела с 3 с? Постройте графики пути.

3. На рисунке приведены графики зависимости пути от времени для двух автомобилей. Скорость которого из автомобилей больше? Почему вы так считаете?

Видео:Физика 7 кл (2013 г) Пер §17 Упр 4 №4 . График зависимости скорости равномерного движения тела от врСкачать

Графики равномерного прямолинейного движения (Колебошин С.В.)

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На этом уроке мы узнаем, как графическим методом описать прямолинейное равномерное движение. Научимся строить график такого движения по закону или с помощью графика записывать закон движения. Также узнаем геометрический смысл графика зависимости проекции скорости от времени и решим несколько типовых задач на данную тему.