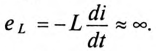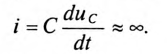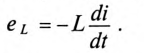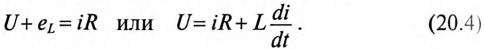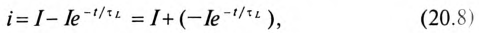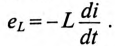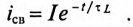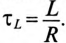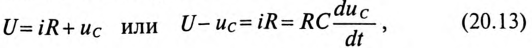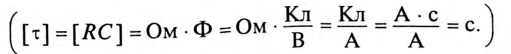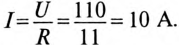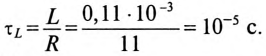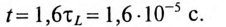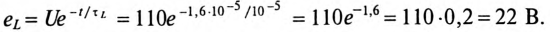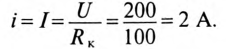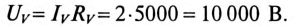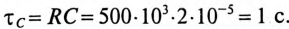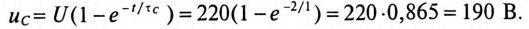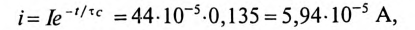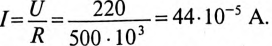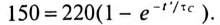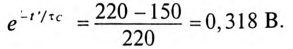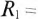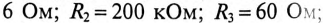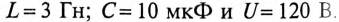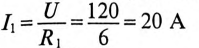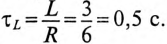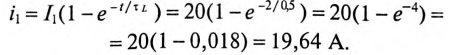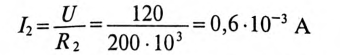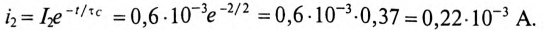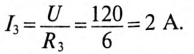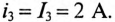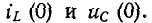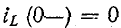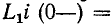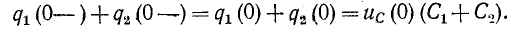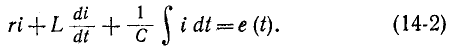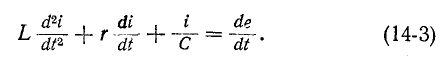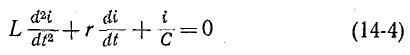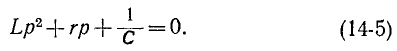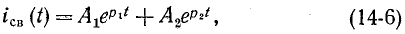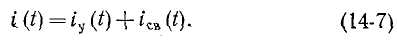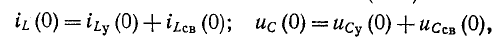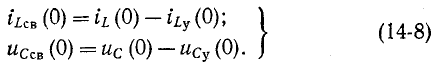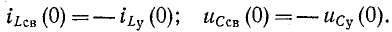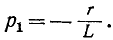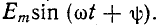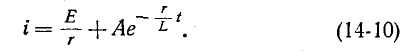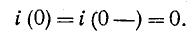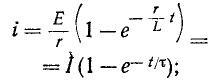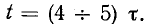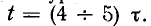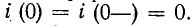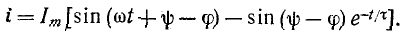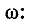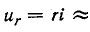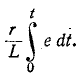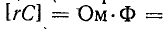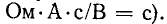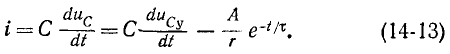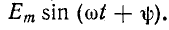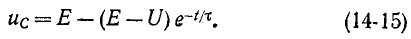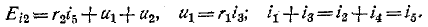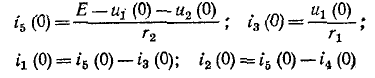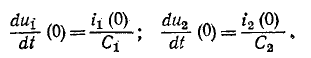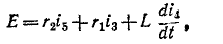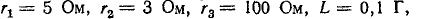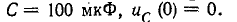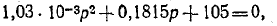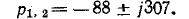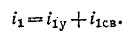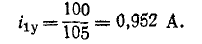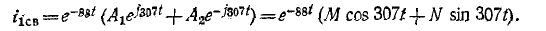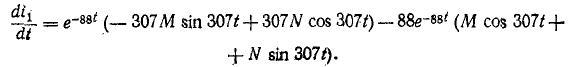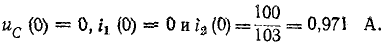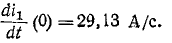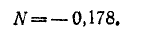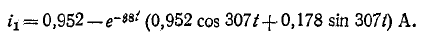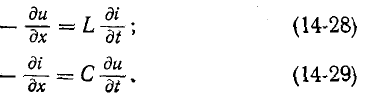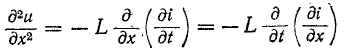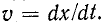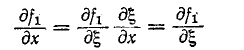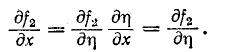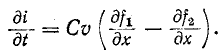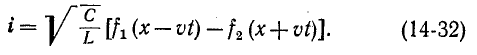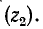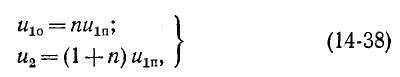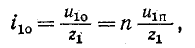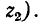При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи.
При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи.
Основные методы анализа переходных процессов в линейных цепях:
- Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
- Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
- Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
- Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
- Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).
Классический метод расчета
Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.
В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями, приведенными в табл. 1.
Таблица 1. Связь мгновенных значений напряжений и токов на элементах электрической цепи
| Резистор (идеальное активное сопротивление) | ||||||||||
| Катушка индуктивности (идеальная индуктивность) | ||||||||||
| Конденсатор (идеальная емкость) | ||||||||||
 . . | (1) |
Подставив в (1) значение тока через конденсатор

получим линейное дифференциальное уравнение второго порядка относительно

В общем случае уравнение, описывающее переходный процесс в цепи с n независимыми накопителями энергии, имеет вид:
 , , | (2) |
где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); 

Порядок данного уравнения равен числу независимых накопителей энергии в цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой из исходной путем объединения индуктивностей и соответственно емкостей элементов, соединения между которыми являются последовательными или параллельными.
В общем случае порядок дифференциального уравнения определяется соотношением
 , , | (3) |
где 



Наличие индуктивных связей на порядок дифференциального уравнения не влияет.
Как известно из математики, общее решение уравнения (2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю. Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (2), применительно к электротехнике в качестве последнего удобно принять решение 

Частное решение 

Вторая составляющая 

В соответствии с вышесказанным, общее решение уравнения (2) имеет вид
 | (4) |
Соотношение (4) показывает, что при классическом методе расчета послекоммутационный процесс рассматривается как наложение друг на друга двух режимов – принужденного, наступающего как бы сразу после коммутации, и свободного, имеющего место только в течение переходного процесса.
Необходимо подчеркнуть, что, поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении искомой переменной х, справедлив только для линейных цепей.
Начальные условия. Законы коммутации
В соответствии с определением свободной составляющей 


Таблица 2. Законы коммутации
Первый закон коммутации (закон сохранения потокосцепления)
Магнитный поток, сцепленный с катушками индуктивности контура, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: 
Второй закон коммутации (закон сохранения заряда)
Электрический заряд на конденсаторах, присоединенных к любому узлу, в момент коммутации сохраняет то значение, которое имел до коммутации, и начинает изменяться именно с этого значения: 
Доказать законы коммутации можно от противного: если допустить обратное, то получаются бесконечно большие значения 

На практике, за исключением особых случаев (некорректные коммутации), допустимо использование указанных законов в другой формулировке, а именно:
первый закон коммутации – в ветви с катушкой индуктивности ток в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: 
второй закон коммутации – напряжение на конденсаторе в момент
коммутации сохраняет свое докоммутационное значение и в дальнейшем начинает изменяться с него: 
Необходимо подчеркнуть, что более общей формулировкой законов коммутации является положение о невозможности скачкообразного изменения в момент коммутации для схем с катушкой индуктивности – потокосцеплений, а для схем с конденсаторами – зарядов на них. В качестве иллюстрации сказанному могут служить схемы на рис. 2, переходные процессы в которых относятся к так называемым некорректным коммутациям (название произошло от пренебрежения в подобных схемах малыми параметрами, корректный учет которых может привести к существенному усложнению задачи).
Действительно, при переводе в схеме на рис. 2,а ключа из положения 1 в положение 2 трактование второго закона коммутации как невозможность скачкообразного изменения напряжения на конденсаторе приводит к невыполнению второго закона Кирхгофа 

Зависимыми начальными условиями называются значения остальных токов и напряжений, а также производных от искомой функции в момент коммутации, определяемые по независимым начальным условиям при помощи уравнений, составляемых по законам Кирхгофа для 

Пример. Определить токи и производные 

В соответствии с законами коммутации


На основании второго закона Кирхгофа для момента коммутации имеет место

и 
Для известных значений 

определяется 
Значение производной от напряжения на конденсаторе в момент коммутации (см. табл. 1)

Корни характеристического уравнения. Постоянная времени
Выражение свободной составляющей 
Таблица 3. Выражения свободных составляющих общего решения
Вид корней характеристического уравнения
Выражение свободной составляющей
Корни 
Корни 
Пары комплексно-сопряженных корней
Необходимо помнить, что, поскольку в линейной цепи с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.
При вещественных корнях 
Поскольку физически колебательный процесс связан с периодическим обменом энергией между магнитным полем катушки индуктивности и электрическим полем конденсатора, комплексно-сопряженные корни могут иметь место только для цепей, содержащих оба типа накопителей. Быстроту затухания колебаний принято характеризовать отношением

которое называется декрементом колебания, или натуральным логарифмом этого отношения

называемым логарифмическим декрементом колебания, где 
Важной характеристикой при исследовании переходных процессов является постоянная времени t , определяемая для цепей первого порядка, как:

где р – корень характеристического уравнения.
Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго. Однако на практике считается, что он заканчивается при
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.
- Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.
- Теоретические основы электротехники. Учеб. для вузов. В трех т. Под общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
- Переходные процессы в электрических цепях
- Переходный процесс в электрической цепи
- Подключение катушки индуктивности к источнику с постоянным напряжением
- Отключение и замыкание RL-цепи
- Зарядка, разрядка и саморазрядка конденсатора
- Переходные процессы в электрических цепях. Классический метод расчета
- Законы коммутации и начальные условия
- Установившийся и свободный режимы
- Переходный процесс в цепи r, L
- Переходный процесс в цепи r, С
- Включение в цепь r, С постоянной э. д. с.
- Переходные процессы в цепях с распределенными параметрами
- Расчеты переходных процессов в электрических сетях
- Оглавление
- Зачем вообще что-то рассчитывать в энергетике?
- Переходные процессы – это…
- Переходные процессы и режим реального времени
- Нельзя просто так взять и рассчитать переходный процесс
- Куда и как запустить модель?
- Управление по управлению всеми управлениями
- Все уже сделано до нас
- 📺 Видео
Видео:Расчет переходного процесса через ДИФФЕРЕНЦИАЛЬНОЕ уравнение по законам Кирхгофа│Классический методСкачать

Переходные процессы в электрических цепях
Содержание:
Переходные процессы в электрических цепях:
Переходный процесс в электрической цепи — это электромагнитный процесс, возникающий в электрической цепи при переходе от одного установившегося (принужденного) режима к другому. Установившимся (принужденным) называется режим работы электрической цепи, при котором напряжение и токи цепи в течение длительного времени остаются неизменными.
Такой режим в электрической цепи устанавливается при длительном действии источников постоянной или переменной ЭДС при неизменных параметрах этой цепи R, L и С.
Переходный процесс вызывается коммутацией в цепи. Коммутацией называется процесс замыкания или размыкания рубильников или выключателей. Переходный процесс может быть вызван изменением параметров электрической цепи R, L или С.
Переходный процесс базируется на двух законах коммутации:
- ток в индуктивности не может изменяться скачком;
- напряжение на емкости не может изменяться скачком.
Действительно, если ток в индуктивности L изменяется скачком, т. е. мгновенно, то ЭДС самоиндукции eL становится бесконечно большой (при
В реальных цепях ЭДС самоиндукции может иметь только конечные значения.
Если в цепи с емкостью С напряжение на ее обкладках изменяется скачком, т. е. мгновенно, то появляется бесконечно большой зарядный (или разрядный) ток (при 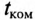
Ток в электрических цепях может иметь только конечные значения.
Переходный процесс является быстропротекающим процессом, длительность которого обычно составляет десятые, сотые и даже миллионные доли секунды и сравнительно редко — секунды и даже десятки секунд.
Таким образом, один установившийся режим цепи отделяется от другого некоторым промежутком времени, в течение которого происходит постепенный переход от прежнего состояния цепи к новому.
Переходный процесс в линейных цепях можно рассматривать как результат наложения двух процессов:
- нового установившегося режима, который наступает после коммутации;
- свободного процесса, обеспечивающего переход цепи от прежнего установившегося режима к новому установившемуся режиму.
Таким образом, ток i цепи в течение переходного процесса можно представить суммой двух токов: нового установившегося 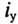
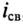
Аналогично напряжение в течение переходного процесса равно
В результате переходного процесса происходят изменения тока, напряжения, фазы, частоты и т.д.
Изучение переходных процессов очень важно, так как оно позволяет выявить возможные превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, позволяет выявить возможные броски токов, величина которых в десятки раз превышает установившийся. Изучение переходных процессов позволяет выявить ситуации, возникающие в электрических цепях при коротком замыкании, резком включении и выключении рубильников, и прочие режимы работы цепи.
Видео:Переходные процессы | Классический метод расчета переходных процессов. Теория и задачаСкачать

Переходный процесс в электрической цепи
Переходный процесс в электрической цепи — это процесс, возникающий в электрической цепи при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, когда при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.
Подключение катушки индуктивности к источнику с постоянным напряжением
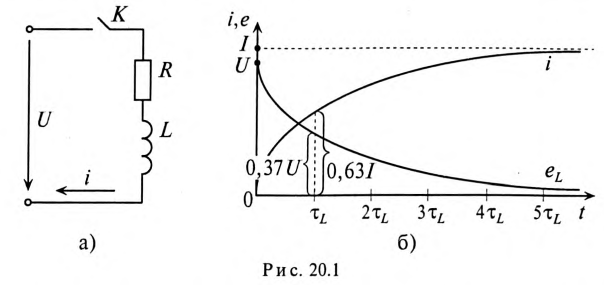
Если катушку индуктивности (RL) подключить к источнику с постоянным напряжением U (замыкание ключа К), то ток i в не-разветвленной цепи (рис. 20.1а) будет увеличиваться от нуля (в начале переходного процесса) до установившегося значения
Установившийся, т.е. постоянный, ток I не индуктирует в катушке ЭДС самоиндукции, поэтому индуктивное сопротивление в установившемся режиме при условии (20.3) отсутствует.
Этот увеличивающийся ток i индуктирует в индуктивности L катушки ЭДС самоиндукции (см. (9.11))
Следовательно, для любого момента времени переходного процесса по второму закону Кирхгофа можно записать
Разделив уравнение (20.4) на R, получают
В уравнении (20.5) 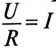
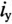
Отношение — 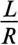
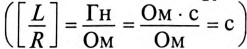
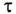
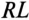
Тогда уравнение (20.5) можно записать в виде
Если это уравнение проинтегрировать, предварительно разделив переменные (ток и время), а затем спотенцировать, то получим выражение
где е — основание натурального логарифма (е=2,71); I — установившийся ток (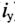
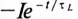
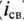
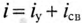
Таким образом, уравнение, которое позволяет определить вели-шу тока в цепи с индуктивностью L в любой момент переходно-процесса RL-цепи при подключении реальной катушки индук-1Вности к источнику с постоянным напряжением U, записывается в виде
Воспользовавшись Приложением 9, по выражению (20.10) можно определить, что за время t= 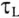
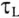
Теоретически переходный процесс происходит бесконечно долго. Практически переходный процесс в рассматриваемой цепи считается законченным, когда ток i увеличивается до 99 % установившегося тока I.
Как видим, чем больше xL, тем больше времени t длится перечный процесс.
Таким образом, постоянная времени xL определяет скорость греховного процесса или его длительность.
ЭДС самоиндукции в рассматриваемой цепи, вызванная свободным током 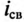
Таким образом, ЭДС самоиндукции в 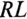
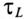
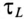
Увеличение тока и уменьшение ЭДС самоиндукции катушки при подключении катушки к источнику с постоянным напряжением U показаны на графике рис. 20.1б.
Отключение и замыкание RL-цепи
Если цепь с катушкой, в которой проходит установившийся ток I (рис. 20.1а), разомкнуть, то ток i в такой цепи с большой скоростью уменьшается до нуля и в катушке индуктируется большая ЭДС самоиндукции eL
Эта ЭДС полностью приложена к клеммам ключа, так как при размыкании сопротивление ключа становится бесконечно большим. Эта ЭДС вызывает значительное увеличение электрического поля между контактами ключа, а следовательно, и напряженности поля. Большая напряженность электрического поля может вызвать искровой и даже дуговой разряд между размыкающимися контактами ключа, в результате чего обгорают контакты ключа.
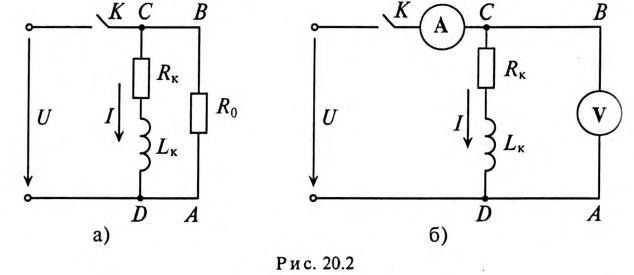
Поэтому рубильники в RL-цепях шунтируются специальными устройствами, которые обеспечивают гашение дугового разряда. Для гашения дугового разряда необходимо одновременно с отключением катушки индуктивности от источника замкнуть ее на разрядное сопротивление R0 (рис. 20.2а).
Уменьшение тока 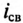
Наглядно это уменьшение можно наблюдать на рис. 20.1б, если кривую изменения eL считать кривой уменьшения тока 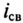
Постоянная времени при отключении катушки от источника с постоянным напряжением U определяется как и при включении катушки на это напряжение, т.е.
Если катушку с установившимся током I, зашунтированную сопротивлением Ro (рис. 20.2а), отключить от источника (разомкнуть ключ К), то в замкнутом контуре ABCD в начальный момент коммутации 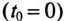
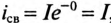
Для определения активного сопротивления катушки 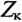
Как видно, за счет переходных процессов в цепях с индуктивностью возникают большие токи и напряжения. С этим необходимо считаться и учитывать при проектировании и эксплуатации цепей с индуктивностью.
Зарядка, разрядка и саморазрядка конденсатора
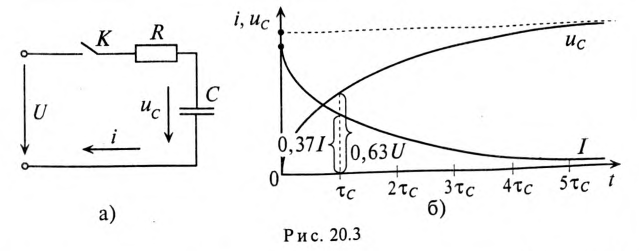
Если конденсатор с сопротивлением (утечки) R и емкостью С подключить к источнику с постоянным напряжением U (замыканием ключа К), то в цепи (рис. 20.3а) появится ток зарядки конденсатора (см. (11.16)):
где 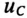
По второму закону Кирхгофа для цепи зарядки конденсатора (рис. 20.3а) можно записать уравнение
где произведение RC имеет размерность времени, обозначается буквой 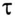
Уравнение (20.13) можно записать в виде
Если в уравнении (20.15) разделить переменные, проинтегрировать, а затем спотенцировать, то получится выражение
где U — установившееся напряжение 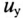
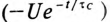
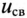
Следовательно, напряжение на заряжающемся конденсаторе в любой момент времени t переходного процесса определяется выражением
По (20.17), пользуясь Приложением 9, можно определить, что за время t= 
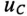

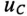
Теоретически зарядка конденсатора длится бесконечно долю а практически конденсатор считается заряженным, когда напряжение на нем достигает 99 % напряжения источника U.
Таким образом, и в RC-цепи, чем больше постоянная времени 

Ток i при зарядке конденсатора (см. (20.13)) уменьшается по за кону
(20. IS)
где 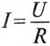
За время t= 

Графики изменения напряжения на конденсаторе и тока в цепи арядки конденсатора изображены на рис. 20.36.
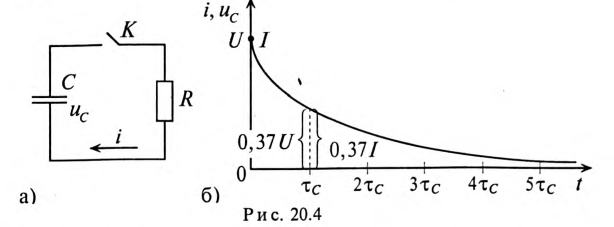
Если конденсатор емкостью С, заряженный предварительно до напряжения U, разряжать через резистор с сопротивлением R рис. 20.4а), то напряжение 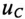
где U — напряжение на конденсаторе до начала разрядки (при t= 0), а 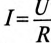

За время t= 
Если конденсатор емкостью С, заряженный до напряжения U, отсоединить от источника, то он будет разряжаться через свой диэлектрик. Напряжение на нем будет уменьшаться по закону 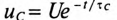
Постоянная времени саморазряда зависит от физических свойств диэлектрика
где р — удельное сопротивление диэлектрика; 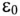
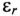
Для определения напряжения, тока, ЭДС в любой момент переходного процесса 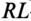
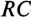
Пример 20.1
Катушка электромагнита с параметрами 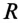
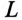
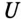
Решение
Установившийся ток
Постоянная времени для катушки
Подставляем значение величин в (20.10):
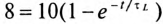
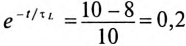
По Приложению 9 определяется 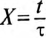
ЭДС самоиндукции за время 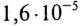
Пример 20.2
К зажимам катушки индуктивности с параметрами 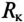
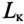
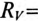
Определить напряжение на зажимах вольтметра и ток в обмотках прибора (обмотки соединены последовательно) при t=0, если размыкание рубильника К произойдет мгновенно и дуги не возникнет.
Решение
До размыкания рубильника через катушку проходил ток
В момент размыкания рубильника (t = 0) весь этот ток проходит обмоткам вольтметра. При этом на вольтметре напряжение cтанет равным
Такого напряжения (10 кВ) и такого тока (2 А) обмотка вольтметра (обычно подвижная обмотка электродинамического прибора рассчитана на ток порядка десятков, максимум, сотен миллиампер) не выдержит и сгорит.
При размыкании рубильника с конечной скоростью между расходящимися контактами рубильника К (рис. 20.26) возникнет электрическая дуга. Это приведет к тому, что увеличение напряжения на вольтметре и тока через обмотки вольтметра будет меньше, чем в рассмотренном выше случае (мгновенное размыкание рубильника). Однако меры предосторожности для сохранения вольтметра и рубильника, описанные выше, нужно соблюдать.
Пример 20.3
Конденсатор емкостью С= 2 мкФ через сопротивление R= 500 кОм подключается к источнику с постоянным напряжением U= 220 В.
Определить напряжение на конденсаторе 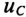
Решение
Постоянная времени заряда конденсатора
Напряжение на конденсаторе через 2 с от начала заряда
Ток в цепи заряда конденсатора через 2 с от начала заряда
так как
Время t’ заряда конденсатора до напряжения 150 В определяется по формуле (20.17):
Откуда
Из таблицы показательных функций (Приложение 9) находят t’= 1,14 с.
Пример 20.4
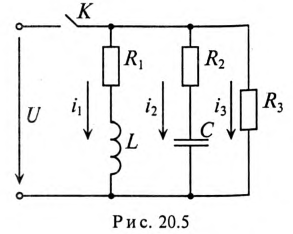
Параметры цепи, изображенной на рис. 20.5, следующие:
Определить значение токов в ветвях через время t= 2 с после замыкания ключа К.
Решение
Для ветви (1) с индуктивностью определяются:
установившийся ток
и постоянная времени
Тогда ток через 2 с будет равен
Для ветви (2) с емкостью определяются:
максимальный установившийся ток по окончании переходного процесса
и постоянная времени 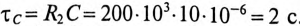
Тогда ток зарядки через 2 с будет равен
Для ветви (3) с активным сопротивлением 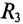
Постоянная времени 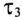
Через 2 с значение тока будет таким же, т. е.
Видео:Урок 4. Расчет цепей постоянного тока. Законы КирхгофаСкачать

Переходные процессы в электрических цепях. Классический метод расчета
Возникновение переходных процессов:
В предыдущих главах рассматривались установившиеся процессы в линейных электрических цепях, т. е. такие процессы, при которых напряжения и токи либо неизменны во времени (цепи постоянного тока), либо представляют собой периодические функции времени (цепи переменного тока).
Наступлению установившегося процесса, отличного от первоначального режима работы цепи, предшествует, как правило, переходный процесс, при котором напряжения и токи изменяются непериодически.
Переход от одного режима работы цепи к другому может быть вызван изменением параметров или схемы цепи, называемым в общем случае в электротехнике коммутацией.
Можно теоретически считать, что коммутация цепи производится мгновенно, т. е. на включение, выключение или переключение цепи время не расходуется. Тем не менее переход от исходного режима работы цепи к последующему установившемуся процессу происходит не мгновенно, а в течение некоторого времени. Объясняется это тем, что каждому состоянию цепи соответствует определенный запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей. Энергия 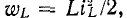
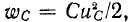
Если исключить случаи размыкания индуктивности и замыкания накоротко емкости и рассматривать цепи, в которых энергия, накапливаемая в магнитном или электрическом поле, может рассеиваться в виде теплоты в сопротивлениях, то, считая, что коммутация происходит мгновенно, можно искрообразование не учитывать.
Для завершения переходного и наступления установившегося процессов теоретически требуется бесконечно большое время. Практически, однако, время переходного процесса определяется малым интервалом, по истечении которого токи и напряжения настолько приближаются к установившимся значениям, что разница оказывается практически неощутимой. Чем интенсивнее происходит рассеяние энергии в сопротивлениях, тем быстрее протекает переходный процесс.
Если бы электрическая цепь состояла только из сопротивлений и не содержала индуктивностей и емкостей, то переход от одного установившегося состояния к другому совершался бы мгновенно, без затраты времени. В реальных электротехнических устройствах тепловые потери, обусловленные током, магнитные и электрические поля сопутствуют друг другу. Применяя специальные схемы и подбирая соответствующие параметры цепи, можно в зависимости от необходимости ускорить или замедлить переходный процесс.
В одних случаях переходные процессы в электрических цепях нежелательны и опасны (например, при коротких замыканиях в энергетических системах). В других случаях переходный процесс представляет собой естественный, нормальный режим работы цепи, как это, например, имеет место в радиопередающих и радиоприемных устройствах, системах автоматического регулирования и других цепях.
Существуют различные методы расчета переходных процессов в линейных электрических цепях. Настоящая глава посвящена классическому методу решения дифференциальных уравнений, описывающих переходные процессы.
Законы коммутации и начальные условия
Высказанные выше положения о том, что запас энергии магнитного или электрического поля может изменяться только плавно, без скачков, выражают принцип непрерывности во времени потокосцепления индуктивности и электрического заряда емкости и называются законами коммутации.
Невозможность скачкообразного изменения потокосцепления следует из того, что в противном случае на индуктивности появилось бы бесконечно большое напряжение 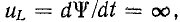
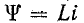
Аналогично невозможность скачкообразного изменения электрического заряда q следует из того, что в противном случае через емкость проходил бы бесконечно большой ток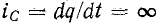
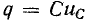
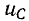
При этом следует отметить, что в цепях с идеализированными сосредоточенными параметрами скачкообразно могут изменяться: 1) токи в сопротивлениях и емкостях и 2) напряжения на сопротивлениях и индуктивностях.
Значения тока в индуктивности и напряжения на емкости в момент коммутации называются независимыми начальными условиями.
Обычно принимают, что коммутация происходит в момент времени t= 0; тогда ток в индуктивности и напряжение на емкости в момент времени непосредственно перед коммутацией обозначаются через 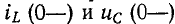
На основании законов коммутации: 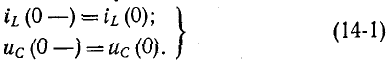
Эти равенства выражают начальные условия цепи, в которых происходит коммутация.
При нулевых начальных условиях, т. е. косца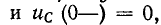
В случае ненулевых начальных условий, т. е. когда 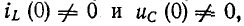
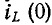
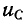
Независимые начальные условия характеризуют энергию магнитного и электрического полей, запасенную к моменту коммутации, и для расчета переходного процесса обязательно требуется знание этих начальных условий, причем совершенно безразлично, каким образом эти условия в цепи были созданы.
При расчете переходных процессов в разветвленных электрических цепях наряду с независимыми начальными условиями используются так называемые зависимые начальные условия, а именно: значения токов, напряжений и их производных в начальный момент времени (t = 0).
До сих пор нами исключались из рассмотрения случаи коммутации, при которых неизбежно между контактами возникает искра или дуга. Один из таких случаев показан на рис. 14-1, а. До коммутации ток проходит через индуктивность 
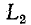
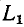
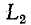
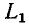
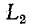
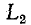
замкнуться и через межвитковую емкость. После быстрого погасания дуги токи в 
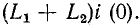
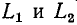
Найденный таким образом ток 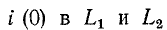
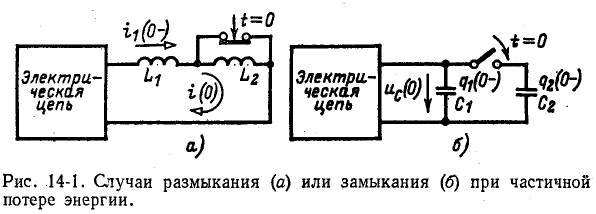
При коммутациях в цепях с емкостями при отсутствии сопротивлений также возможны весьма быстрые перераспределения зарядов, условно рассматриваемые как мгновенные. В этом случае применим принцип непрерывности суммарного заряда. Полученные при этом значения зарядов и напряжений на отдельных емкостях используются в расчете последующего переходного процесса как независимые начальные условия.
Например, в случае схемы на рис. 14-1, б принцип непрерывности суммарного заряда до и после коммутации выражается равенством
При сделанном допущении в остальной электрической цепи, соединенной с емкостями, не возникает бесконечно большого тока, так как суммарный заряд не изменяется скачкообразно при t=0.
В процессе рассматриваемой коммутации энергия электрического поля уменьшится, так как часть ее превратится в тепло в очень малом сопротивлении проводника при очень большом токе, а также сможет выделиться в искре и излучиться.
Установившийся и свободный режимы
В общем случае анализ переходного процесса в линейной цепи с сосредоточенными параметрами r, L, С и М сводится к решению обыкновенных линейных неоднородных дифференциальных уравнений, выражаюших законы Кирхгофа. Эти уравнения представляют собой линейную комбинацию напряжений, токов, их первых производных и интегралов по времени.
Например, если какая-нибудь э. д. с. е (t) включается в цепь, состоящую из последовательно соединенных r, L и С, то интегродифференциальное уравнение имеет вид:
Это уравнение после дифференцирования приводится к неоднородному дифференциальному уравнению второго
Как известно, общий интеграл такого^ уравнения равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Частное решение выражает установившийся режим, задаваемый источником.
Расчеты установившихся токов рассмотрены в предыдущих главах.
Общее решение физически определяет поведение цепи при отсутствии внешних источников электрической энергии и заданных начальных условиях. Функции, определяемые общим решением, называются свободными составляющими (токов, напряжений и пр.).
В случае, рассмотренном выше, однородное уравнение имеет вид:
и соответствующее ему характеристическое уравнение
Если корни характеристического уравнения обозначить через 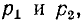
где 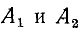
Полный переходный ток в цепи равен сумме установившегося и свободного токов:
Аналогично напряжение, заряд, магнитный поток и другие функции на любом участке цепи в переходном режиме состоят из установившейся и свободной составляющих.
На основании законов коммутации можно найти начальные независимые условия 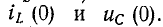
откуда
Итак, начальные значения свободных функций 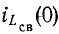
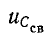
В частном случае при нулевых начальных условиях:
В зависимости от порядка дифференциальных уравнений, описывающих исследуемые переходные процессы, различают цепи первого, второго и более высокого порядков.
В цепях первого порядка накопление энергии происходит только в одном элементе, L или С в форме магнитной энергии, или электрической энергии . Одноконтурная цепь, содержащая элементы, в которых накапливается энергия обоих видов — магнитная « электрическая, представляет собой цепь второго порядка . Разветвленные цепи могут быть более высокого порядка.
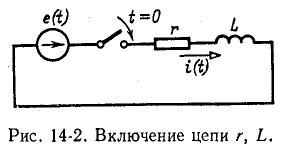
Переходный процесс в цепи r, L
Положим, что в момент t = 0 цепь, состоящая из сопротивления r и индуктивности L, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-2).
Дифференциальное уравнение для времени 
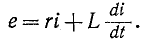
Характеристическое уравнение имеет вид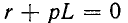
Отсюда свободный ток
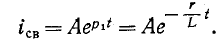
Переходный ток в цепи определится суммой установившегося и свободного токов:
Установившийся ток может быть найден, если задана э. д. с. е (t).
Рассмотрим три случая:
1) включение в цепь г, L постоянной э. д. с. £;
2) короткое замыкание цепи г, L
3) включение в цепь г, L синусоидальной э. д. с.
1. Включение в цепь г, L постоянной э. д. с.
При включении в цепь г, L постоянной э. д. с. Е установившийся ток равен Е’/г. Поэтому согласно (14-9)
Постоянная интегрирования А находится по начальному условию
Согласно уравнению (14-10) при t — 0
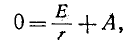
откуда 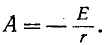
здесь 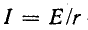
В начальный момент t = 0 э. д. с. самоиндукции 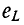
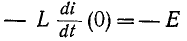
С течением времени э. д. с. самоиндукции убывает, а ток в цепи возрастает, асимптотически приближаясь к установившемуся значению.
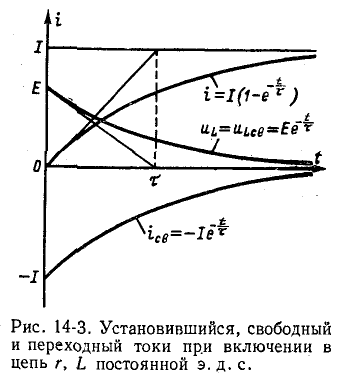
На рис. 14-3 показаны кривые установившегося, свободного и переходного токов; на том же рисунке изображена кривая напряжения на индуктивности 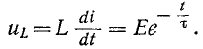
Из курса математического анализа известно, что если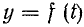
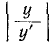
Величина 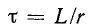
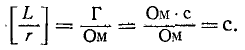
Выражение (14-11) показывает, что постоянная времени графически определяется длиной подкасательной к кривой 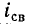
Нарастание тока происходит тем быстрее, чем меньше постоянная времени и соответственно чем быстрее убывает э. д. с. самоиндукции. Для различных моментов времени ток в цепи, выраженный в процентах конечного (установившегося) значения составляет:
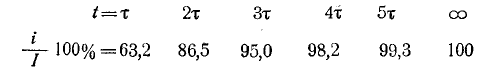
Следовательно, постоянная времени цепи г, L равна промежутку времени, в течение которого свободная составляющая тока убывает в е = 2,718 раза и соответственно ток в этой цепи, включенной на постоянное напряжение, достигает 63,2% своего установившегося значения.
Как видно из рис. 14-3 и приведенной выше таблицы», переходный процесс теоретически длится бесконечно долго. Практически же можно считать, что он заканчивается спустя
2. Короткое замыкание цепи r, L.
Положим, что цепь r, L, присоединенная к источнику постоянного или переменного напряжения, замыкается при t = 0 накоротко (рис. 14-4, а). В образовавшемся при этом контуре r, L благодаря наличию магнитного поля индуктивной катушки ток исчезает не мгновенно: э. д. с. самоиндукции, обусловленная убыванием магнитного потока, стремится поддержать ток в контуре за счет энергии исчезающего магнитного поля.
По мере того как энергия магнитного поля постепенно рассеивается, превращаясь в сопротивлении г в тепло, ток в контуре приближается к нулю.
Процесс, происходящий в короткозамкнутом контуре г, L, является свободным; установившийся ток в данном случае равен нулю.
Положив в (14-9) 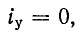
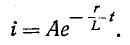
Постоянная интегрирования А находится из начального условия
здесь i (0—) — значение тока в индуктивности в момент, непосредственно предшествовавший короткому замыканию; оно может быть положительным или отрицательным.
На рис. 14-4, б изображены кривые спада тока в короткозамкнутом контуре и кривая напряжения на индуктивности

Постоянная времени контура 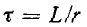
Переходный процесс в короткозамкнутом контуре заканчивается теоретически при 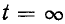
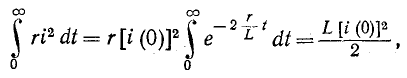
т. е. вся энергия, запасенная в магнитном поле катушки до коммутации.
Так же как и в предыдущем случае, переходный процесс в короткозамкнутом контуре можно практически считать законченным спустя
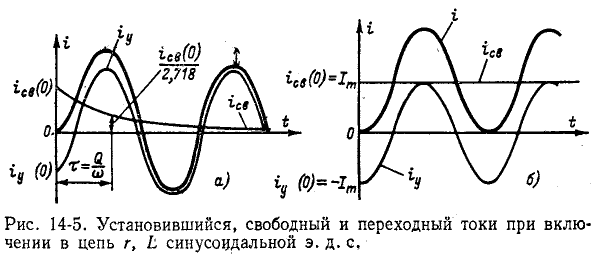
3. Включение в цепь r, L синусоидальной э. д. с.
При включении в цепь r, L синусоидальной э. д. с. 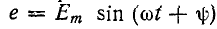
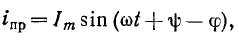
где 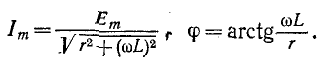
На основании (14-9) 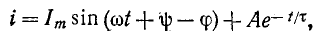
где 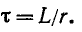
Постоянная интегрирования определяется по начальному условию
Следовательно, 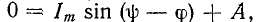
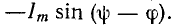
На рис. 14-5, а изображены кривые 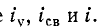
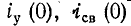
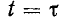
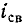
контура Q и обратно пропорциональна частоте 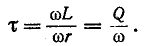
Если в момент коммутации (t = 0) ток 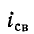
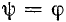
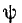
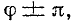
Если же коммутация происходит при 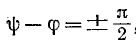
а именно 
гает экстремального значения (положительного или отрицательного) в конце первого полупёриода. Однако даже в предельном случае, когда r= 0 и, следовательно, 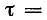
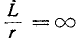
При достаточно большой постоянной времени 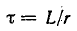
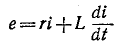
можно пренебречь по сравнению со вторым слагаемым, приняв приближенно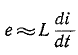
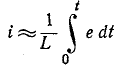
Следовательно, цепь с последовательно соединенными сопротивлением и индуктивностью при большой постоянной времени можно рассматривать как интегрирующее звено.
В свою очередь при достаточно малой постоянной времени, пренебрегая вторым слагаемым уравнения, приближенно получаем:
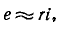
откуда
.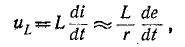
т. e. цепь с последовательно соединенными сопротивлением и индуктивностью при малой постоянной времени представляет собой дифференцирующее звено.
В обоих случаях функция е(t) может быть произвольной.
Интегрирующие и дифференцирующие звенья входят в качестве элементов в системы автоматического управления и регулирования.
Переходный процесс в цепи r, С
Положим, что в момент t = О цепь, состоящая из сопротивления г и емкости С, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-6).
На основании второго закона Кирхгофа уравнение для времени t 
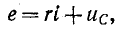
где 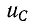
С учетом того, что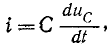
получим:
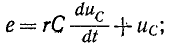
здесь искомой величиной является напряжение на емкости.
Характеристическое уравнение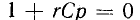
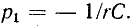
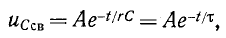
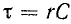
Переходное напряжение на емкости равно сумме принужденного и свободного напряжений:
В свою очередь ток в контуре
Рассмотрим три случая:
1) включение в цепь г, С постоянной э. д. с.
2) короткое замыкание цепи r, С
3) включение в цепь r, С синусоидальной э. д. с.
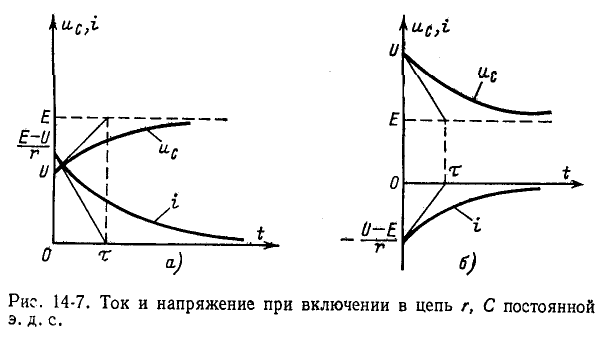
Включение в цепь r, С постоянной э. д. с.
Включим постоянную э. д. с. Е в цепь с сопротивлением г и предварительно заряженной емкостью С (полярности заряженной емкости указаны на рис. 14-6 знаками + и —); начальное напряжение на емкости
(0) обозначим для простоты через U.
Установившееся напряжение на емкости равно э. д. с. источника. Поэтому согласно (14-12)
Постоянная интегрирования А, входящая в (14-14), находится по начальному условию:
При t = 0 имеем 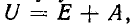
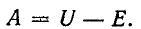
Согласно (14-13) ток в контуре
Если Е > U, то с течением времени напряжение на емкости возрастает, стремясь к установившемуся значению Е, а ток убывает, стремясь в пределе к нулю; на рис. 14-7, а изображены кривые нарастания 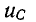
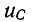
Если Е 0), убывающей (с 0) или убывающей (с 1 В случае, когда э. д. с. изменяется в виде импульса, имеющего кусочно-аналитическую форму, представляется часто целесообразным применять интеграл Дюамеля
токи же 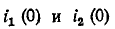
Подстановка в эти уравнения найденных значений 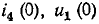
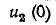
Начальное значение производной тока в индуктивности определяется также из уравнения Кирхгофа:
откуда при t = О
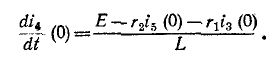
Пример (4-2. Определить ток i в иепи на рис. 14-17, если известно, что е = E = 100 В,
Подстановка заданных значений в приведенное выше характеристическое уравнение дает:
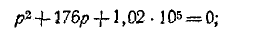
корни характеристического уравнения комплексные:
В начальный момент 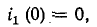
Производная тока по времени
В начальный момент
Следовательно, в начальный момент напряжение на ветви 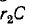
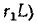
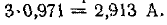
производной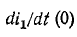
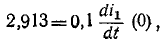
Следовательно, подставляя значение 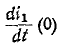
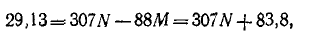
откуда
Итак,
Переходные процессы в цепях с распределенными параметрами
Переходные процессы в цепях с распределенными параметрами (в линиях, обмотках электрических машин и т. п.) возникают при коммутациях, передаче непериодических сигналов или под влиянием внешнего электромагнитного поля (например, при грозовых разрядах). Для исследования переходных процессов в однородных цепях с распределенными параметрами пользуются дифференциальными уравнениями (11-2) в частных производных: 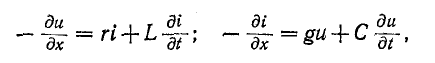
где r, L, g и С — параметры цепи на единицу длины; х — координата рассматриваемой точки, отсчитываемая от начала цепи.
В общем виде решение этих дифференциальных уравнений достаточно сложно. Решение упрощается, если пренебречь потерями В этом случае
е. считать, что r и g равны нулю.
Дифференцируя (14-28) по х:
и используя (14-29), получаем: 
Дифференциальное уравнение (14-30) известно в математической физике под названием уравнения ко—лебаний струны. Его решение дано Даламбером и имеет вид: 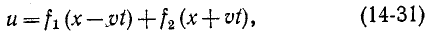
где 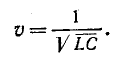
Первая слагающая представляет собой одиночную прямую волну напряжения, которая без изменения перемещается в сторону возрастающих х, т. е. от начала к концу цепи. Для всех значений х, при которых 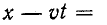
Вторая слагающая представляет собой одиночную о б -ратную волну напряжения, которая без изменения перемещается в противоположном направлении.
Для нахождения тока произведем замену переменных, обозначив 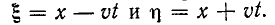
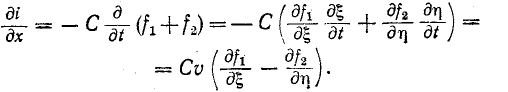
Но
Интегрирование последнего уравнения дает 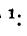
Выражения (14-31) и (14-32) записываются сокращенно:
здесь 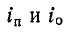
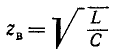
Следовательно, напряжение и ток прямой и соответственно обратной волн связаны законом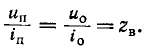
Аналогичный результат был получен для установившихся прямой и обратной волн при рассмотрении синусоидального режима в однородной линии. Физически установившиеся волны представляют собой бесконечные суммы прямых и обратных одиночных волн, отраженных от обоих концов линии.
Итак, при отсутствии потерь в однородной цепи с распределенными параметрами напряжение и ток могут быть представлены как сумма и разность двух волн, движущихся с одинаковой скоростью 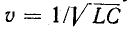
Если на пути распространения волны встречается неоднородность, например воздушная линия переходит в кабельную или волна достигает конца линии (разомкнутого или замкнутого через сопротивление или на короткое), происходит отражение волны. В зависимости от характера неоднородности отражение может быть частичным или полным. В первом случае наряду с отраженной волной возникает преломленная волна, распространяющаяся за место нарушения однородности; во втором случае преломленная волна отсутствует.
Обозначим 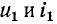
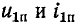
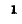
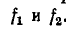
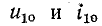
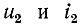
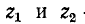
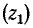
В месте неоднородности выполняется условие равенства
напряжений и токов: 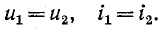
Следовательно, 
Подстановка в (14-36) значений 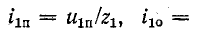
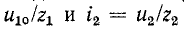
В результате совместного решения уравнений (14-35) — (14-37) находятся отраженная 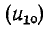
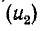
где 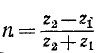
Соответственно ток отраженной волны
а ток преломленной волны
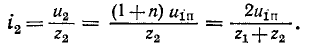
Последнее выражение показывает, что ток в конце линии после отражения можно найти как ток в эквивалентной цепи, в которую включается напряжение, равное двойному напряжению падающей волны, и которая состоит из волнового сопротивления первой линии 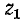
Опишем процесс включения однородной линии без потерь. После присоединения линии к источнику э. д. с. по линии начнет распространяться зарядная волна, создающая напряжение и ток. Если в конце линии присоединена нагрузка, равная волновому сопротивлению линии,
то падающая волна, достигнув ее, не отразится и в линии сразу наступит установившийся режим. Если же нагрузка с линией не согласована, то падающая зарядная волна, достигнув конца линии, претерпит отражение. Распространяясь в обратную сторону, отраженная волна сложится с падающей, причем напряжения волн суммируются, а токи вычитаются (алгебраически). Достигнув начала линии, обратная волна снова отразится от источника э. д. с., как от короткозамкнутого конца; появится новая прямая волна напряжения и тока, которая также отразится от конца, и т. д. Процесс будет продолжаться до наступления установившегося режима. Теоретически в идеальной линии без потерь при чисто реактивной нагрузке процесс колебаний будет продолжаться бесконечно долго. В реальной линии при наличии потерь волны напряжения и тока будут постепенно затухать в направлении распространения.
Напряжение и ток в линии в произвольный момент времени определятся как алгебраические суммы и соответственно разности напряжений и токов прямых и обратных волн.
Пользуясь формулами и схемой замещения, описанной выше, можно найти напряжение и ток, возникающие в месте присоединения сосредоточенной нагрузки или перехода одной линии в другую (см. пример 14-3).
Следует отметить что индуктивность, включенная последовательно в линию, или емкость, включенная параллельно проводам линии, сглаживает фронт преломленных волн; активное сопротивление, включенное в линию параллельно, уменьшает преломленную волну.
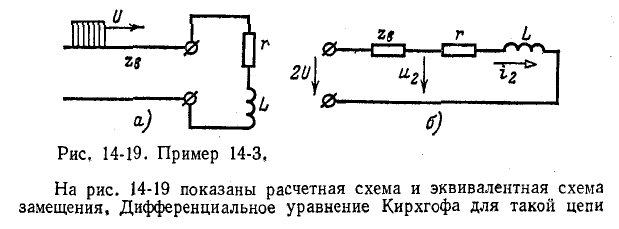
Пример 14-3. К концу линии, имеющей волновое сопротивление 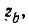
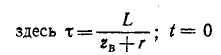
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Переходные процессы в линейных цепях
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами
- Переходные процессы в колебательных контурах
- Цепи с взаимной индукцией
- Трехфазные цепи
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Видео:Цепи переменного тока. Комплексные значения сопротивлений, токов и напряжений в цепи. Задача 1Скачать

Расчеты переходных процессов в электрических сетях
Энергетика – обширная сфера деятельности, и расчеты в ней производятся разные: расчет рентабельности строительства новых станций, расчет перенапряжений, расчет оставшегося времени до конца рабочего дня в пятницу вечером. Все эти темы в одной статье не уместить, поэтому сконцентрируюсь на той, которой занимался в течение последних лет, – расчеты переходных процессов в электрических сетях. Кому интересно, что это такое и как оно происходит в современном мире, – прошу под кат.
Оглавление
Видео:Урок 358. Активное сопротивление в цепи переменного тока. Действующее значение тока и напряженияСкачать

Зачем вообще что-то рассчитывать в энергетике?
Причины довольно стандартны для любой технической/инженерной сферы: экономия, безопасность, нормативы и прочие банальности. Несколько примеров:
- Чем точнее мы знаем, какие перенапряжения могут возникнуть, тем меньше денег можно затратить на изоляционный материал, имеющий достаточный запас прочности.
- Чем больше информации имеется о резонансных частотах в сети, тем точнее можно настроить систему управления и эффективнее справляться с воздействием внешних факторов.
- Чем детальнее изучено поведение оборудования в тех или иных режимах, тем проще соблюсти нормативы, пройти сертификацию или приёмку.
- И т. д.
- И т. п.
Что объединяет приведенные выше примеры? То, каким образом можно получить всю эту интересующую нас информацию. Те, кто помнит название статьи, уже догадались: это можно сделать, рассчитав переходные процессы.
Впрочем, если у вас есть деньги и время для проведения экспериментов, то можно одними расчетами не ограничиваться, ведь теория – это хорошо, а теория, подкрепленная экспериментами, – еще лучше. Правда это может быть долго, дорого и не всегда возможно, ведь ставить эксперименты на работающей энергосистеме – это, выражаясь местным сленгом, сродни запуску тестов на продакшн сервере – если что-то пойдет не так, то мало не покажется.
Видео:Пример 7 | Классический метод расчета цепи 1-го порядка с конденсаторомСкачать

Переходные процессы – это…
Если по-простому, переходный процесс – это когда токи и напряжения в электрической сети изменяются во времени вследствие различных событий, таких как короткие замыкания, отключения выключателей, удары молнии и проч. и проч. Переходные процессы – явления чаще всего временные. В электроэнергетике они могут длиться как нано- и микросекунды (переключение транзисторов, удары молнии), так и несколько минут или часов (межсистемные колебания, электромагнитные бури).
Рассчитать переходный процесс – значит узнать, как именно изменяются токи и напряжения.
Переходные процессы обычно плавно перетекают в установившиеся. В установившемся процессе, если опять же по-простому, величины токов и напряжений постоянны. «А как же напряжение в розетке, которое меняется 50 раз в секунду?» – спросите вы. В принципе, это тоже можно рассматривать как непрекращающийся переходный процесс, но если амплитуда, частота и фаза синусоидального сигнала постоянны, то гораздо удобнее рассматривать как установившийся. Для этого существуют свои методы, но об этом как-нибудь в другой раз.
Вот, например, напряжения на конденсаторе при подключении его к трехфазной сети 10 кВ (если что, конденсаторов на самом деле три – по одному на каждую фазу):
Где-то сейчас замигали лампочки
Вопрос: когда начинается переходный процесс?
Вопрос со звездочкой: когда заканчивается переходный процесс и начинается установившийся?
Видео:Расчет цепи с ИСТОЧНИКОМ ТОКА по законам КирхгофаСкачать

Переходные процессы и режим реального времени
Есть еще одна область применения расчетов переходных процессов – это расчеты в реальном времени. Если обычно все гонятся за уменьшением времени расчетов, то здесь, наоборот, очень важно, чтобы расчет одной секунды проходил ровно за одну секунду. Это применяется, например, для прототипирования, тестирования и отладки устройств, предназначенных для взаимодействия с реальным миром: систем управления, защиты и т.д.
Поясню на примере: система управления электростанцией знает, что для реакции на событие X электростанции понадобится две секунды, а на событие Y – три. Чтобы дебажить эту систему управления, её подключают не к реальной электростанции, а к так называемому симулятору, имитирующему поведение электростанции. Симулятор в реальном времени рассчитывает переходные процессы, которые происходили бы в электростанции, и ведет себя соответствующе: отвечает на событие X за две секунды, а на Y – за три вне зависимости от количества ядер процессора и тактовой частоты. Система управления при этом думает, что работает с реальной электростанцией.
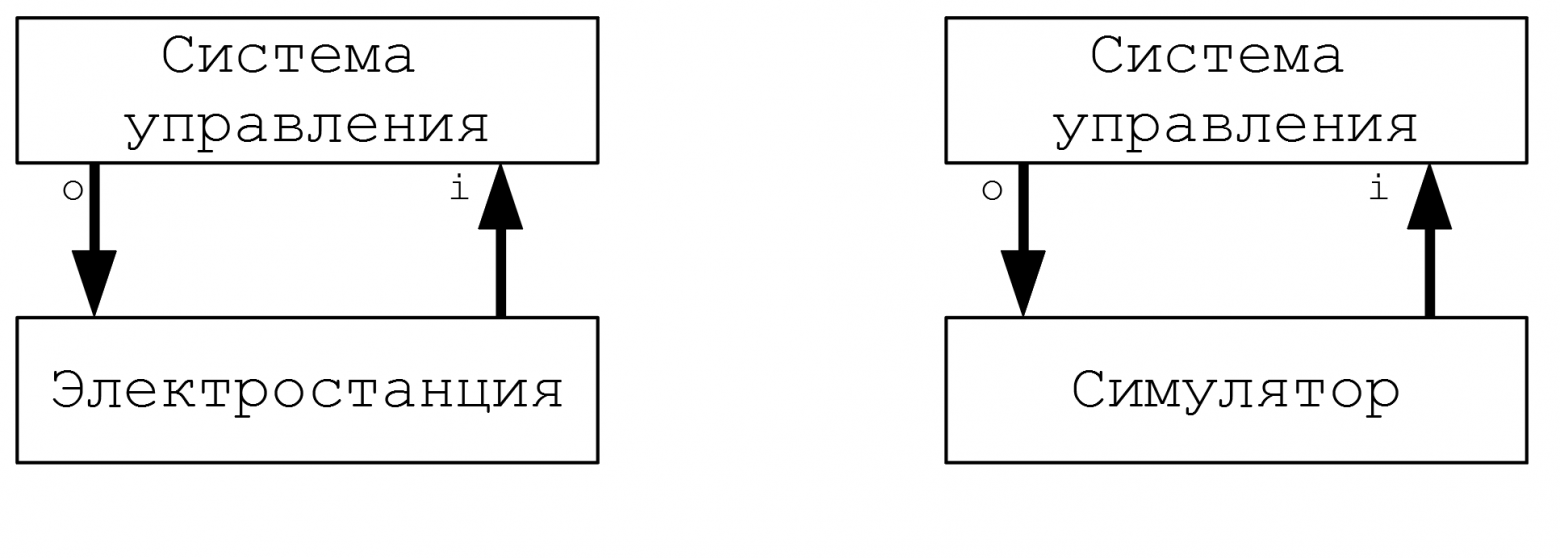
Слева: система управления и электростанция дружно работают на благо родины.
Справа: ничего не подозревающая система управления коварно обманута и подключена к симулятору
Видео:Лекция 122. Переходные процессыСкачать

Нельзя просто так взять и рассчитать переходный процесс
В рассчитываемой электрической сети могут иметься тысячи различных компонентов, поэтому ручной расчет переходных процессов практически неприменим к реальным задачам в электроэнергетике – все считается на компьютере. Расчеты переходных процессов в реальном времени производить вручную еще сложнее, ведь вам понадобится еще и секундомер.
В начале расчета стоит определиться, какая от него требуется информация. Например, нам нужно узнать перенапряжения, возникающие при коротком замыкании в преобразователе постоянного тока на морской ветроэлектростанции. С типом расчетов всё и так понятно из названия статьи – нужно рассчитывать переходные процессы.
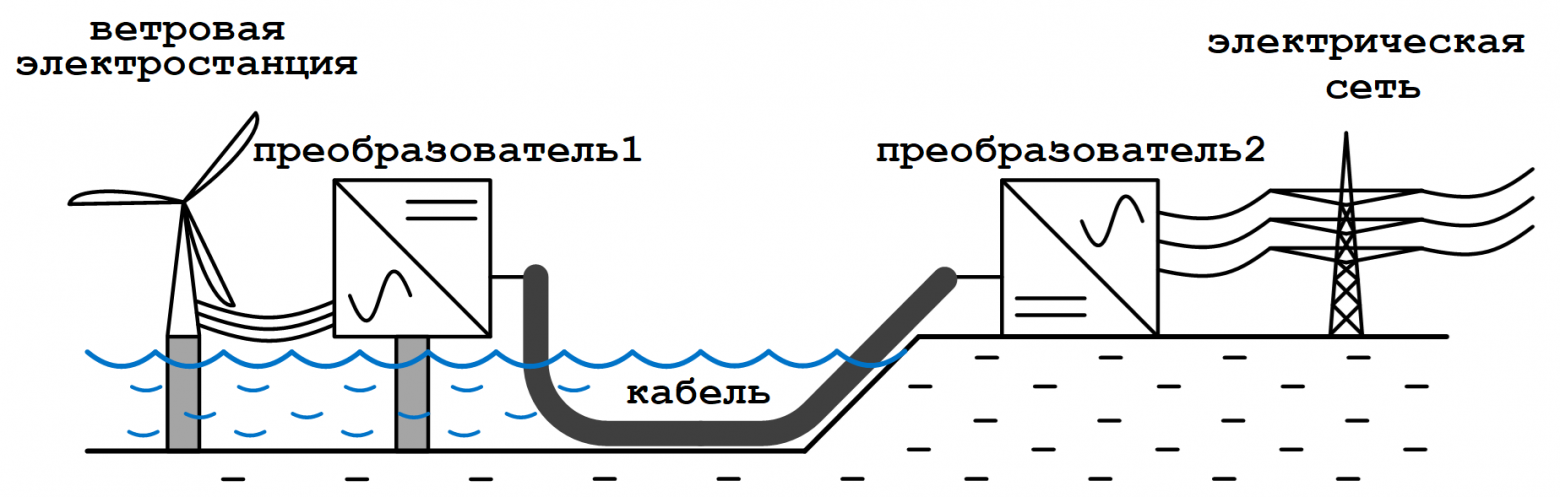
Вот так схематично эта система может выглядеть
Затем нужно разработать математическую модель рассчитываемой системы: ветровой электростанции, преобразователей, кабеля и прилегающей электрической сети. Этот этап может быть довольно сложным, ведь не всегда сразу ясно, насколько детальны должны быть модели. Чем больше деталей, тем точнее результат, но тем больше времени надо потратить на расчеты. Никто не любит долго ждать, поэтому приходится искать компромисс. Часто для удовлетворительной точности требуются многие десятки дифференциальных и не очень уравнений для каждого устройства.
Как только модель системы у нас появилась, можно запустить её в солвер (об этом чуть дальше), задать начальные условия и все рассчитать. Как происходит типичный расчет:
- Интересующий период времени разбивается на отрезки с шагом интегрирования ∆t. Чем меньше шаг интегрирования, тем медленнее процесс расчета и точнее результаты. Часто используются величины ∆t от единиц до десятков микросекунд.
- Величины токов и напряжений в момент времени (t-∆t) используются для расчета величин на следующем моменте времени (t).
- Начальные условия, т. е. начальные величины токов и напряжений, находятся из предположения, что в момент времени t=0 был установившийся режим.
Когда расчет закончен, можно использовать результаты по назначению (ну или обнаружить перенапряжения в миллиарды вольт и понять, что кто-то перепутал плюс с минусом).
Видео:Электротехника. Переходные процессы часть 4Скачать

Куда и как запустить модель?
Основу ПО для расчета переходных процессов составляет солвер – программа, решающая систему уравнений. Особую популярность в области переходных процессов имеют солверы, основанные либо на методе узловых потенциалов, либо на методе пространства состояний. Метод пространства состояний подходит для практически любых систем дифференциальных уравнений, а в методе узловых потенциалов используются законы Ома и Кирхгофа, что делает его удобным именно для электрических систем.
Дифференциальные уравнения математических моделей нужно привести к удобоваримому для солвера виду, т. е. к превратить их в систему линейных алгебраических уравнений. Для этого применяется численное интегрирование. Часто используется метод трапеций, его и рассмотрим. Все уравнения ветровой электростанции из предыдущей главы здесь писать не буду, ограничусь одним скромным конденсатором. Ток и напряжение на нем связывает дифференциальное уравнение вида
Применим суть метода трапеций на двух последовательных моментах времени (t-∆t) и (t):
А теперь вынесем величины для момента времени (t-∆t) в отдельное слагаемое:
Тем, кому хочется попробовать свои силы самостоятельно, предлагаю разделаться таким же образом с уравнением для индуктивности.
Величины для момента времени (t-∆t) вынесены в отдельное слагаемое, т. к. известны из расчета предыдущего момента времени. Теперь вместо дифференциального у нас есть обычное линейное алгебраическое уравнение. Если подключить фантазию, то можно заметить, что финальное уравнение очень похоже на резистор, подключенный параллельно с источником тока.
Аналогичным образом уравнения других элементов приводятся к комбинациям резисторов и источников тока. А такие электрические схемы умеет решать каждый уважающий себя солвер, основанный на методе узловых потенциалов.
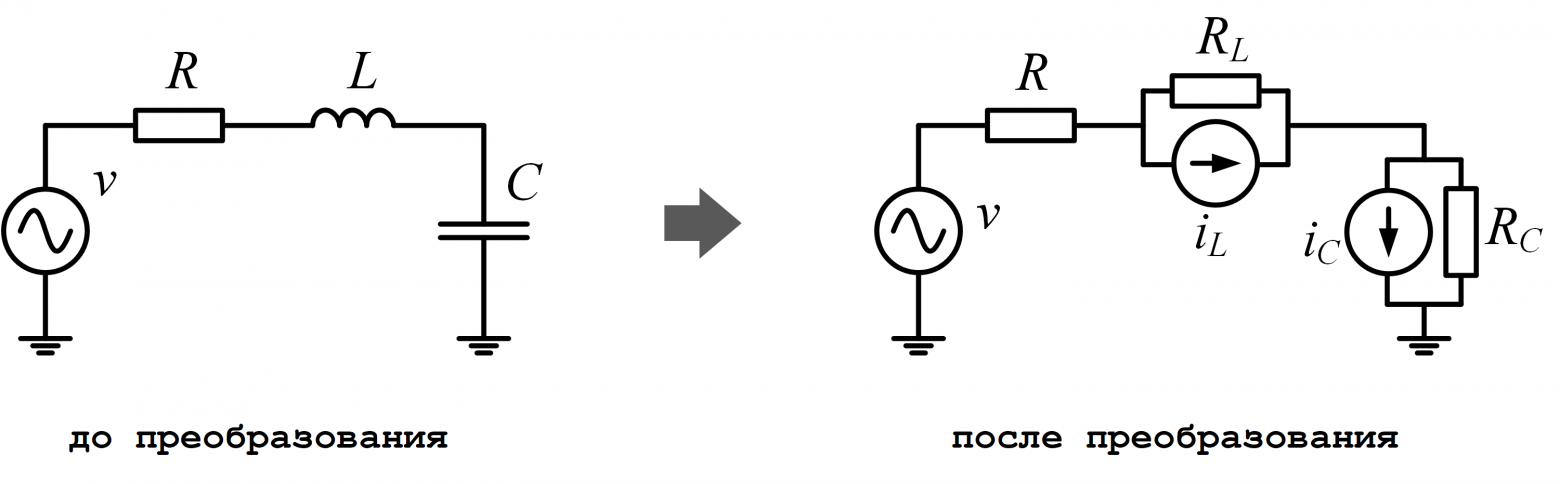
Легким движением руки схема превращается…
Не все элементы в электрических сетях представляются в виде резисторов и источников тока, но все в итоге представляются в виде линейных алгебраических уравнений, которые можно скормить солверу. А если не представляются в виде линейных, то можно линеаризовать, рассчитать якобиан, применить метод Ньютона, но все равно решить, пусть и с итерациями. Но не будем сильно углубляться, об этом тоже как-нибудь в другой раз.
Видео:Метод контурных токов - определение токов. ЭлектротехникаСкачать

Управление по управлению всеми управлениями
В реальных электрических сетях очень часто используются системы управления: в электроприводе, в ветровых генераторах, в преобразователях постоянного/переменного тока и т. д. Они оказывают сильное влияние на переходные процессы, поэтому их тоже приходится учитывать в расчетах.
Сложность уравнений в системах управления теоретически ограничена лишь фантазией инженеров: дискретные передаточные функции пятого порядка? Пожалуйста. Синус от логарифма? Дайте два, один гиперболический. Из-за этого солвер для систем управления часто приходится использовать отдельный, посложнее.
Впрочем, часто системы управления «однонаправлены», т. е. сигналы приходят с датчиков, проходят обработку и отправляются в управляющие устройства (типа транзисторов) без каких-либо самозацикливаний. Расчет такой системы управления относительно прост, ведь можно последовательно применять всякие алгебраические операции и горя не знать.

Два сложения, два умножения и один интеграл. Легкотня!
Видео:Урок 17. Как работает Интегрирующая и Дифференцирующая RC-цепь | Самое понятное объяснениеСкачать

Все уже сделано до нас
Ну а если не хочется самому разрабатывать модели и солверы, можно воспользоваться уже существующими программными продуктами. Приведу лишь широко известные в узких кругах энергетиков программы, ибо составить исчерпывающий список – задача не из простых. У меня бэкграунд скорее энергетика, чем электронщика, поэтому некоторые популярные программы со схожим функционалом из области электроники наверняка пропустил. Если знаете что-то похожее – поделитесь в комментариях.
- EMTP: специализированное ПО для расчета переходных процессов в электрических сетях. Может использоваться и для расчета установившихся процессов
- ATP: то же самое
- PSCAD: то же самое
- PowerFactory: то же самое
- Simulink: популярен, знаменит, много методов интегрирования. Но для электрических сетей с большим количеством элементов подходит с трудом. А для прототипирования – очень даже.
- SimPowerSystems: надстройка над Simulink’ом специально для электрических систем.
- Hypersim: расчеты в реальном времени
- RTDS: тоже расчеты в реальном времени
- PSS/E: может как и в установившиеся, так и в переходные процессы
- LTspice: с упором на электронику
Половина этих продуктов из Канады: EMTP, PSCAD, SimPowerSystems, Hypersim, RTDS. Не скажу, с чем связан такой интерес канадцев к переходным процессам, но разбираются они в них не хуже, чем в хоккее.
📺 Видео
Урок 25. Что такое Переменный ТОК | Практические примерыСкачать

Расчет цепей переменного синусоидального тока | Метод комплексных амплитуд | Часть 3Скачать

Расчет цепи при t(0+)│Зависимые начальные условия │КЛАССИЧЕСКИЙ МЕТОДСкачать

Переходные процессы. Расчет RL цепи с Двойной коммутацией. График переходного процессаСкачать

[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]Скачать
![[ТАУ]Записать передаточную функцию устройства [Составить диф. ур-е для условия передачи напряжения]](https://i.ytimg.com/vi/agDRxLaUWI4/0.jpg)
Урок 353. Колебательный контурСкачать

Классификация четырехполюсников. Системы уравнений четырехполюсниковСкачать

2020 г. Дифференциальные уравнения для электрических цепей. Лекция и практикаСкачать


 ;
; ,
,
 ;
;