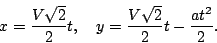Видео:Часть 1. Скорость и ускорение в сферической системе координатСкачать

Уравнение годографа вектора скорости
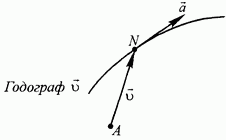
- Уравнение движения декартовой точки известно. Получить уравнение годографа вектора скорости. На фиг. 9а показана траектория в момент времени и несколько векторов скорости в различные моменты времени в выбранном масштабе.
Регулярная прецессия гироскопа характеризуется собственным вращением и постоянной угловой скоростью прецессии, причем прецессия образуется вокруг оси в определенном направлении и под определенным углом. Людмила Фирмаль
На рисунке 9б показан годограф этого вектора скорости движения. Точка M (x, y, z) на траектории соответствует точке M (…, zj) на годографе вектора скорости. Согласно определению годографа, координаты точки Л / представляются проекцией вектора скорости на координатную ось OjXjjjjZi по формуле.
- Если ось координат годографа вектора скорости параллельна оси относительных координат с учетом точечного уравнения движения, Z T М / х, у, зл Рисунок 9 rX) = vx = x; v „t = vy = y; vZt = vz = z. Параметрическое уравнение годографа вектора скорости имеет вид: Xj = x; yt = y; zr = z. Удаление параметра t из этих уравнений дает уравнение годографа для вектора скорости в координатной форме.
При получении постоянной вращающейся траектории вместо вертикального приближения Asym, как описано выше, получается наклонная асимптота в том или ином направлении в зависимости от направления вращения. Людмила Фирмаль
Годограф вектора скорости обеспечивает визуальное представление скорости движущейся точки в различные моменты времени. Кроме того, ускорение параллельно касательной к годографу вектора скорости, поэтому можно определить направление вектора ускорения.
Если вам потребуется помощь по теоретической механике вы всегда можете написать мне в whatsapp.




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Видео:Лекция 22. Декартова система координат на плоскости и полярная система координатСкачать

Годограф скорости
ГОДОГРАФ СКОРОСТИ. Пусть точка перемещается по некоторой траектории АВ. В каждый момент времени вектор скорости (v) направлен по касательной к траектории в соответствующем положении точки, причем v = dr/dt, где r — радиус-вектор, определяющий положение точки на кривой по отношению к некоторой системе отсчета с произвольным началом О (фиг. 1). Вектор ускорения (а) равен производной вектора (v) по времени (t) а = dv/dt. Если от некоторой произвольной точки О1 откладывать векторы h = v, то, при перемещении точки по своей траектории, вектор (h) будет менять в общем как свою абсолютную величину, так и направление, имея одно и то же начало О1. Конец вектора (h) будет описывать кривую, называемую годографом скорости. Так как вектор (h) для кривой А1В1 играет ту же роль, что вектор (r) для кривой АВ, то скорость конечной точки вектора (h), при ее перемещении по А1В1, равна
Таким образом, видно, что вектор ускорения точки, движущейся по некоторой траектории, равняется в каждый момент соответствующему вектору скорости конца вектора, описывающего годограф скорости. Плоскость, касательная к годографу скорости и проходящая через (h), будет, очевидно, параллельна плоскости, проходящей через (а) и (v), т. е. она будет параллельна соприкасающейся плоскости кривой АВ.
При прямолинейном равномерном движении (v = Const) годограф скорости стягивается в одну точку. Если точка перемещается по кривой, имея одну и туже линейную скорость (v = Const), то годограф скорости представляет собой кривую, описанную на шаровой поверхности радиуса (v).
При плоском движении, годограф скорости — плоская кривая. Для свободной материальной точки, брошенной под углом к горизонту с некоторой начальной скоростью v0, имеем: v = v0 + gt, где v — вектор скорости точки по истечении времени (t), а g = Const — вектор ускорения силы тяжести. Так как h0 = v0 = Const, а вектор (gt) сохраняет постоянно вертикальное направление, то конец вектора (h = v) постоянно лежит на вертикали, т. е. годограф скорости для рассматриваемого случая представляет собой вертикальную прямую (фиг. 2).
Если точка описывает конического сечение с постоянной секториальной скоростью относительно фокуса конического сечения, то годограф скорости представляет собой окружность. Годограф скорости впервые был рассмотрен Гамильтоном, а затем Мёбиусом.
Источник: Мартенс. Техническая энциклопедия. Том 5 — 1929 г.
Видео:Скорость и ускорение точки в полярных координатахСкачать

Ускорение
Вы будете перенаправлены на Автор24
Средним ускорением $leftlangle arightrangle $ называется отношение приращения скорости $triangle v=vleft(t+triangle tright)-vleft(tright) $ к длительности промежутка времени $triangle t$, в течение которого оно произошло: $leftlangle arightrangle =frac$
В декартовых координатах это уравнение эквивалентно системе трёх уравнений:
Модуль вектора ускорения
Конец вектора скорости $overrightarrow$ при движении материальной точки описывает кривую, называемую годографом скорости (рис.2).
Рисунок 1. Годограф скорости
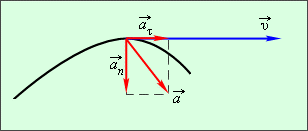
Ускорение в каждой точке годографа скорости направлено по касательной к годографу в этой точке. Следовательно, направление вектора ускорения $overrightarrow$ в случае криволинейного движения не совпадает с направлением вектора скорости $overrightarrow$.
Рисунок 2. Касательное и нормальное ускорения
Касательное ускорение $overrightarrow<a_>$ указывает, насколько быстро изменяется скорость тела по модулю, а нормальное ускорение $overrightarrow$ указывает, насколько быстро скорость тела изменяется по направлению.
Из рис. 2 видно, что модуль полного ускорения $a=sqrt<a^2_+a^2_n>$
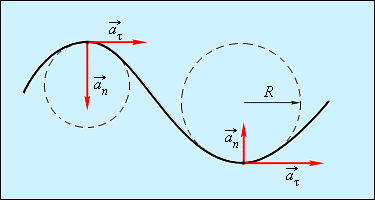
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).
Рисунок 3. Движение по дугам окружностей
Нормальное ускорение $overrightarrow$ зависит от модуля скорости $upsilon $ и от радиуса R окружности, по дуге которой тело движется в данный момент: $a_n= frac$. Вектор $overrightarrow$ всегда направлен к центру окружности.
Определить скорость, ускорение и координату x точки в момент времени, равный 10 c, если уравнение движения материальной точки имеет вид $x=A+Bt+Ct^2$ , где А= 8 м, В = 5 м/c, С = 2 м/c2.
А = 8 м; В = 5 м/с; С = 2 м/с2; t = 10 c. Найти: v — ?, a — ?, x — ?
Определяем координату x в заданный момент времени, подставив в уравнение движения материальной точки значения коэффициентов:
[x=A+Bt+Ct^2=8+3times 10+2times ^2=238 м ]
Определяем мгновенную скорость v материальной точки, как первую производную координаты по времени, и находим скорость материальной точки в заданный момент времени: $v=dot=B+2Ct=5+2times 2times 10=45 м/с$
Определяем ускорение a материальной точки, как первую производную от скорости по времени и находим ускорение материальной точки в заданный момент времени:
[a=dot=2C=2times 10=20 м/с^2]
Ответ: В момент времени t = 10 c координата материальной точки х = 238 м, скорость материальной точки v = $45 м/с$ , ускорение материальной точки а = $20 м/с^2$
Готовые работы на аналогичную тему
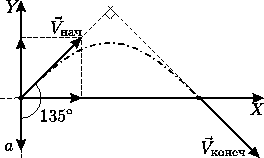
Космический корабль движется в открытом космосе со скоростью $overrightarrow$. Требуется изменить направление скорости на 90 градусов, оставив величину скорости неизменной. Найдите минимальное время, необходимое для такого манёвра, если двигатель может сообщать кораблю в любом направлении ускорение, не превышающее $a$. По какой траектории будет при этом двигаться корабль?
Перейдём в инерциальную систему отсчёта, движущуюся с постоянной скоростью $overrightarrow$. Так как во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково (принцип относительности Галилея), то ограничение, наложенное в условии задачи на ускорение корабля, не изменится. В новой системе отсчёта начальная скорость космического корабля равна нулю, а конечная скорость по модулю равна $vsqrt$ и направлена под углом к первоначальному направлению движения.
Теперь ясно, что для совершения манёвра нужно включить двигатели так, чтобы при развороте корабля его ускорение было всё время направлено в сторону конечной скорости корабля, то есть под углом 45 градусов к первоначальному направлению движения. Тогда минимальное время манёвра будет равно $tau =frac=frac<Vsqrt>$.
Выясним, по какой траектории будет двигаться корабль при манёвре. Для этого вернёмся в исходную систему отсчёта и направим координатную ось декартовой системы координат в направлении, обратном ускорению, а ось $X$ — перпендикулярно к ней, так, как показано на рисунке. Тогда закон движения в проекциях на эти оси примет вид:
Выражая из первого уравнения время и подставляя его во второе, получим уравнение траектории корабля: $y=x-frac$ , то есть корабль будет двигаться по параболе, аналогично телу, брошенному по углом к горизонту.
💡 Видео
Математика Без Ху!ни. Полярные координаты. Построение графика функции.Скачать

7.2. Скорость точки в прямоугольной системе координатСкачать

Математика 6 класс (Урок№79 - Декартова система координат на плоскости.)Скачать

Метод годографа и центростремительное ускорениеСкачать

Уравнение координат при равноускоренном движенииСкачать

Определение координаты движущегося тела | Физика 9 класс #3 | ИнфоурокСкачать

Урок 18 (осн). Координаты тела. График движения. График скоростиСкачать

Построение кривой в полярной системе координатСкачать

9 класс. Геометрия. Декартовы координаты. Уравнение окружности. Уравнение прямой. Урок #6Скачать

Модель декартовой системы координат.Скачать

Урок 9. Проекции вектора на координатные осиСкачать

Декартова система координат на плоскостиСкачать

Равномерное прямолинейное движение - физика 9Скачать

Лекция 4.1 | Радиус-вектор, скорость и ускорение | Александр Чирцов | ЛекториумСкачать

ДЕКАРТОВЫ КООРДИНАТЫ. Контрольная № 3 Геометрия 9 класс.Скачать

Лекция 6.2 | Угловая и линейная скорость | Александр Чирцов | ЛекториумСкачать

Скорость и перемещение при прямолинейном равноускоренном движении. 9 класс.Скачать