Уравнение годографа отраженной волны ост (7 видео)

Понятие о многократных сейсмических волнах. Кратная волна на сейсмограммах ОСТ и ОПВ.стр 308-310

Многократной отраженно-преломленной волной называют волну, которая вначале несколько раз отразилась от основной границы раздела, а затем, упав на нее под критическим углом, распространяется как головная (преломленная) волна. Многократные отраженно-преломленные волны обычно образуются на неглубоких сильных отражающее-преломляющих границах.

Уравнение годографа m кратной волны на сейсмограмме ОПВ

годографы полнократных волн имеют форму гипербол, вершины которых находятся над мнимыми источниками S* и S*1 и смещаются по восстанию границы с увеличением кратности.

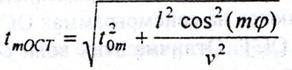
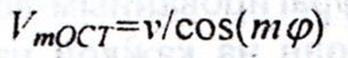
Годографы кратно-отраженных волн на сейсмограммах ОСТ имеют форму гипербол, вершины которых расположены в точке ОСТ: кривизна определяется параметром: .

Кривизны годографов однократных и кратных волн на одних и тех же временах регистрации могут существенно отличаться.

Видео:Ермаков А. П. - Сейсморазведка - Метод отражённых волн (МОВ)Скачать

Лекция 09. Годограф ОСТ. Сейсморегистрирующий канал назначение и реализация.

Марина Власовская 4 лет назад Просмотров:

1 Лекция 09. Годограф ОСТ. Сейсморегистрирующий канал назначение и реализация. Годограф отражённой волны ОСТ Зададим модель с плоской наклонной отражающей границей, характеризующейся эхо-глубиной h s в точке источника и углом падения φ. Начало координат отнесём к точке М, расположенной ровно посередине между источником и приёмником (рис. 1). Рис. 1. Модель Перепишем известное уравнение годографа отражённой волны ОПВ: t= 1 v 4h s 2 4 h s l sin l 2 (1) используя значение эхо-глубины границы, определённое в точке M h M. Из ΔSMK: SKM= 2, MKS = φ, SM =l /2 по определению модели. Следовательно, MK =SM sin = l 2 sin. Но, как очевидно из рисунка, h M =h s MK. Отсюда h s =h M l sin. Подставив полученное выражение в (1), найдём: 2

2 t= 1 v 2 4 h M l 2 cos 2 (2) Формула (2) показывает, что годограф отражённой волны на сейсмограмме ОСТ имеет форму гиперболы, симметричной относительно средней точки М вне зависимости от угла наклона границы. Формулу (2) часто записывают и в другом виде: где t 0 = 2 h M v t= 1 v t 0 и v ОСТ = v cos. 2 l 2 (3) 2 v ОСТ Параметр v ОСТ называется скоростью ОСТ. Хотя скорость и угол наклона границы не связаны друг с другом, удобство использования этого параметра состоит в том, что входящие в него величины v и φ в соответствии с формулой (2) характеризуют кривизну гиперболического годографа отражённой волны. При увеличении v ОСТ кривизна гиперболы уменьшается, а при уменьшении v ОСТ — увеличивается. Поведение осей синфазности различных типов воли на сейсмограммах ОПВ и ОСТ при модели среды с постоянной скоростью приводит к следующим выводам (цит. по Ю.Н. Воскресенский «Построение сейсмических изображений», 2004): на сейсмограмме ОПВ годографы однократных, кратных отражённых и дифрагированных волн проявляются в виде гипербол, вершины которых на плоскости сейсмограммы (x, t) меняют место в зависимости от наклона границ или положения горизонтальных координат точек дифракции; на сейсмограммах ОСТ годографы этих волн проявляются также в виде гипербол, но все эти кривые симметричны относительно общей средней точки. Различие волн на сейсмограммах ОСТ выражается только в разной кривизне их годографов. Это является заме-чательным свойством сейсмограмм ОСТ; кривизны гиперболических годографов на сейсмограммах ОСТ различны. Годографы кратных волн, как правило, имеют большие кривизны, чем годографы однократно отражённых волн. Годографы дифрагированных волн имеют близкие кривизны с годографами однократных отражённых волн. Идея метода ОСТ состоит в объединении трасс, относящихся к одной срединной (или глу

3 бинной) точке, приведении годографов полезных волн этих трасс к горизонтальным линиям и последующем суммировании этих трасс. При обработке трасс подбирают такие временные сдвиги (называемые кинематическими поправками), чтобы гиперболические оси синфазности полезных волн каждой из трасс выпрямились и стали горизонтальными. В то же время оси синфазности кратных волн, обладающие большей кривизной, недоспрямляются. В процессе суммирования импульсы однократных отражённых и дифрагированных волн, складываясь в фазе, усиливаются, а импульсы волн, оси синфазности которых после ввода кинематических поправок остались криволинейными, суммируются не в фазе и ослабляются. Кроме того, происходит ослабление некоррелируемых помех, известно, что при кратности наблюдений F эти помехи после суммирования ослабляются в F раз. Совокупность суммарных трасс, образованных из последовательно расположенных по профилю сейсмограмм ОСТ называется временным разрезом ОСТ (ОГТ). Замечание о терминах ОГТ и ОСТ Под общей средней точкой понимают точку на поверхности земли, находящуюся на середине отрезка, соединяющего ПВ и ПП (рис. 2 а). Средняя точка является общей для ПВ и ПП, расположенных симметрично относительно неё на разных удалениях (рис. 2 б). Сейсмограммой ОСТ называют такую сейсмограмму, которая содержит трассы, относящиеся к фиксированной средней точке профиля. Под общей глубинной точкой (ОГТ) понимают точку (точнее, небольшой участок) на отражающей границе, которая Рис. 2. Понятие ОСТ является общей точкой отражения для всей совокупности трасс заданной сейсмограммы. Проекция общей глубинной точки на линию профиля для горизонтально-слоистой среды всегда совпадает с серединой расстояния ПВ-ПП, то есть с ОСТ. При наклонном залегании сейсмических границ пространственное совпадение координат проекции ОГТ на линию профиля и ОСТ нарушается.

4 Изначально метод, основанный на формировании подобных подборок, назывался «методом общей глубинной точки» (ОГТ); со временем, однако, название изменилось на «метод общей средней точки» (ОСТ), что вернее отражает как суть метода, так и используемые геометрические построения. Сейсморегистрирующий канал Сейсморегистрирующий канал представляет собой совокупность последовательно соединенных устройств, осуществляющих прием механических колебаний почвы, их преобразование в электрические колебания, усиление, преобразование и запись на носитель. Канал состоит из сейсмоприёмника П, усилителя У, фильтров Ф, преобразователя «аналогкод» (также называемого аналогово-цифровым преобразователем) и регистрирующего устройства Р (рис. 3). П У Ф ПАК (АЦП) Р Рис. 3. Состав сейсморегистрирующего канала Сейсмоприёмник, усилитель и фильтры образуют аналоговую часть канала; ПАК и регистратор цифровую. Рассмотрим назначение каждой из частей сейсморегистрирующего канала: Сейсмоприёмник (П) служит для преобразования значений скорости смещения частиц почвы в электрическое напряжение. В настоящее время наиболее распространены инерционные приемники, в которых применяется инерционный принцип измерения механического движения (рис. 4). Существуют также сейсмоприемники давления, Рис. 4. Схема инерционного сейсмоприёмника (по кн. Гурвич, Боганик «Сейсморазведка», 1980 г.). Кр корпус приёмника M инертная масса (груз) N — пружина ЭП электромеханический преобразователь Z электрическое сопротивление При перемещении инертной массы относительно корпуса изменяется магнитный поток, проходящий через витки катушки, являющейся частью преобразователя. Магнитное поле создается постоянными магнитами, соединенными с корпусом прибора или с его инертной массой.

5 которые воспринимают изменения давления, происходящие при распространении упругой волны. От сейсмоприёмника электрические колебания передают по сейсмической косе в сейсморазведочную станцию, где установлена регистрирующая аппаратура. Усилитель (У) служит для изменения уровня сигналов процедурами регулировки. Назначение усилителя приведение (сокращение) естественного динамического диапазона сигнала к диапазону, соответствующему возможностям аппаратуры. Помимо этого, усилитель может обеспечивать повышение уровня сигналов, зарегистрированных на дальних по отношению к ПВ каналах. Фильтры (Ф) производят аналоговую частотную фильтрацию колебаний. Наиболее часто в состав сейсморегистрирующего канала включаются режекторный фильтр для подавления промышленной помехи (50 или 60 Гц), а в обязательном порядке фильтр зеркальных частот (антиаляйсинг-фильтр). Преобразователь «аналог-код» (ПАК) осуществляет дискретизацию (оцифровку) сигнала для его записи на носители. Дискретизация производится по времени (выборка отсчётов с заданным во времени шагом) и по уровню (измерение амплитуды выборки аналогового сигнала и представление измеренного значения в виде двоичного кода ) — см. рис. 5. Рис. 5.Преобразования «аналог-код»: а) дискретизация по времени; б) квантование по уровню. Дискретизация по времени Дискретный сигнал представляет собой последовательность значений, взятых с некоторым, как правило, равномерным, шагом, называемым шагом дискретизации данных. В соответствии с теоремой Котельникова, также известной как теорема отсчётов, тео

6 рема Уиттикера-Найквиста-Шеннона-Котельникова, непрерывный сигнал u(t), имеющий ограниченный спектр шириной f N, может быть однозначно и без потерь восстановлен по своим дискретным отсчётам, взятым через равные интервалы времени, определяемые как t= 1 2 f N (4) Фактически это означает, что при дискретизации сигнала с шагом Δt спектральная плотность сигналов должна быть практически равна нулю на частотах выше частоты Найквиста f N. При наличии спектральной составляющей с частотой f > f N перекрытие соседних членов периодизированного спектра приводит к появлению помехи с частотой, зеркальной относительно f N, т. е. меньшей f N на величину (f — f N ). Эта помеха в дальнейшем не может быть устранена. Поэтому высокочастотные помехи должны быть эффективно подавлены до дискретизации. Так как применяемые для этой цели фильтры нижних частот имеют конечную крутизну среза, то граничная частота фильтра выбирается значительно ниже f N, чтобы на частотах выше f N обеспечивалось достаточно сильное подавление. Пусть полоса пропускания регистрирующей аппаратуры имеет верхнюю граничную частоту f = 125 Гц, а требуемое подавление (

40 дб) достигается на удвоенной граничной частоте. Тогда f N = 250 Гц и Δt = 2 мс. Таким образом, при шаге дискретизации 2 мс обеспечивается неискаженная передача сигналов, верхняя частота спектра которых не превышает 125 Гц. В последних моделях сейсмических станций (Sercel SN388, SN408XL, SN428UL, I/O Image) за счёт изменения дизайна фильтров достигается уровень подавления дб/октава, и в качестве граничных частот можно указывать уровни 0.5 f N, 0.75 f N, 0.8 f N. Дискретизация по уровню Принцип оцифровки амплитуд выборки проще всего понять на примере ранее широко использовавшегося в сейсморазведочных станциях метода поразрядного взвешивания. Он напоминает метод взвешивания груза на весах с двумя чашами, на одну из которых кладется груз, а на другую — гири — эталоны веса. При квантовании по уровню не всегда сигнал совпадает с уровнем квантования. В таком случае поступают одним из следующих способов: 1. значение отсчёта отождествляют с ближайшим значением; 2. значение отсчёта отождествляют с ближайшим меньшим (или большим) значением.

7 Регистратор (Р) осуществляет запись оцифрованного сигнала на носитель. В качестве носителя могут использоваться оптические устройства (CD, DVD, MO-диски), магнитные устройства (жёсткие диски, магнитная плёнка кассеты Exabyte, DLTape; картриджи (3480, 3490) и т.п.). Преимущества цифровой регистрации Внедрение цифровой регистрации сейсмических наблюдений явилось началом весьма важного этапа в развитии сейсмического метода разведки. С одной стороны, это позволило значительно увеличить точность измерения сейсмического поля по сравнению с аналоговой регистрацией, а, с другой стороны, только при цифровой регистрации стало возможным полное использование преимуществ цифровых способов обработки сейсмических данных на ЭВМ. В то же время, цифровая регистрация приводит к значительной автоматизации процесса сбора данных. В настоящее время практически все виды сейсмических исследований проводятся с цифровой регистрацией и последующей обработкой на ЭВМ. Достаточно долгое время количество каналов при регистрации сейсмических данных ограничивалось числом 24, затем пере-шли на 48 каналов и далее на 96. Кроме чисто экономических преимуществ, применение многоканальной регистрации необходимо и для решения задач по повышению геологической эффективности сейсмической разведки. Другой задачей, требующей большого количества каналов регистрации, является многоволновая сейсморазведка, когда нужно регистрировать все три компоненты сейсмического поля. Это относится и к прямой оценке нефтегазоносности по сейсмическим данным. Наконец, трехмерная сейсморазведка (3D), занимающая в настоящее время ведущие позиции, практически не может быть реализована без применения многоканальных и сверхмногоканальных сейсморегистрирующих систем.. Таким образом, значительное увеличение канальности и точности регистрации является одной из основных тенденций в построении современных сейсморегистрирующих систем. Современные многоканальные и сверх-многоканальные сейсморегистрирующие комплексы построены на основе телеметрических принципов сбора информации.

8 Поколения сейсморазведочной аппаратуры Сейсморазведочными станциями первого поколения были станции с прямой осциллографической записью на бумажном носителе. Характерной и главной особенностью конструкций таких станций являлось получение в процессе записи сейсмограммы в окончательном виде, без возможности ее последующего воспроизведения (без производства повторного возбуждения). Пик популярности сейсморазведочных станций первого поколения на производстве пришелся на середину 60-х годов XX века. Работы с использованием станций этого типа при разведке месторождений нефти и газа после 1975 г. практически уже не велись. Главным средством создания воспроизводимой сейсмической записи оказалась магнитная аналоговая запись. С этого времени началась эра сейсморазведочных станций второго поколения — станций с аналоговой магнитной записью. Аппаратура третьего поколения подразумевает использование цифровой записи. Переход к цифровой записи позволил принципиально изменить как качество исходной информации (за счет резкого расширения динамического диапазона), так и качество и результативность обработки получаемой информации за счет последующего более эффективного и широкого применения современной вычислительной техники. Среди систем третьего поколения выделяют два типа систем: 1. системы с линейным разделением каналов 2. телеметрические системы В системе регистрации с линейным разделением каналов линии связи (провода) находятся между сейсмоприемником и сейсмостанцией, составляя для дальних каналов несколько километров. Информация передается в виде аналогового сигнала и претерпевает в процессе передачи значительные искажения, связанные как с взаимными влияниями между каналами и наводками, так и с низкочастотной фильтрацией, обусловленной омическим сопротивлением проводов и электрической емкостью между ними. В телеметрической системе сбора информации сейсмический сигнал преобразуется из аналоговой формы в цифровую до момента передачи в центральный модуль. Все элементы, необходимые для оцифровки сигнала (усилитель, фильтры, преобразователь «аналог-код») находятся непосредственно около сейсмоприёмников. Весь этот набор средств электроники, включая и память для временного хранения информации составляют полевой телеметрический модуль (ПТМ).

Видео:Ермаков А. П. - Сейсморазведка - Сейсмические волны и их кинематические характеристикиСкачать

cos е sin а

Рис. 4.2. Разновидности линейных годографов: а — ОТВ; б — ОТП; в — ОСТ (ОГТ); г — РД

· Годограф общей точки приема (ОТП) — зависимость от дистанции времени прихода волны в одну точку приема С при различных источниках (рис. 4.2, б).

Согласно принципу взаимности, для всякой волны годографы ОТВ и ОТП тождественны, если точки возбуждения и точки приема поменять местами.

· Годограф общей средней точки (ОСТ), называемый также годографом общей глубинной точки (ОГТ), — зависимость от дистанции времени прихода волны при условии совмещения середины всех дистанций в общей точке М (рис. 4.2, в).

Двойное наименование этого годографа сложилось исторически. Сначала он получил название ОГТ, которое в общем случае некорректно, но основательно укоренилось в сейсморазведочной практике, хотя и было позднее заменено более правильным названием ОСТ. Действительно, для всех лучей этого годографа Общая точка зеркальных отражений, расположенная под центром дистанций, существует только в случае простейшего строения разреза — горизонтально-слоистой среды с постоянными пластовыми скоростями. В иных случаях, более реальных на практике, такой общей глубинной точки не существует. В то же время общая средняя точка дистанций всегда имеет место, независимо от строения среды.

Ко второму типу годографов относятся годографы, у которых фиксирована величина дистанции (/ = const) при переменных координатах либо источника, либо приемника, либо средней точки дистанции. Такое представление частного временного поля называют годографом равных дистанций (РД), или равных удалений (РУ). Обычно времена линейного или поверхностного годографа РД относят к средней точке дистанции, которая перемещается в пространстве наблюдений (рис. 4.2, г).

Перечисленные выше годографы отображают времена регистрации некоторой волны на трассах многоканальных сейсмограмм (СГ), имеющих соответствующие названия — СГ ОТВ, СГ ОТП, СГ ОСТ (ОГТ), СГ РД. Из них при полевых наблюдениях получаются только СГ ОТВ. Другие виды сейсмограмм формируются при компьютерной обработке путем сортировки исходных трасс.

Линейный годограф является временной функцией одной переменной и обычно изображается в виде графика как зависимость времени от величины дистанции f = ?(/) с началом оси абсцисс / в общей точке О годографа.

Поверхностный годограф можно изобразить двумя способами. На рис. 4.3, а показана поверхность наблюдений G, расположенная в поле времен, которое задано поверхностями изохрон £. Q₂, Q₃ с временами

/₂. *з> ••• соответственно. Линии K_t, К₂, К_ъ пересечения поверхности G с изохронами являются линиями равных времен (изохрон), изображающими поверхностный годограф. Его можно представить картой изохрон (рис. 4.3,6). По-другому поверхностный годограф изображают в виде временной поверхности Г_с над поверхностью наблюдений G (рис. 4.3, в). Линейный годограф Г_L является сечением поверхностного годографа Г_с вертикальной поверхностью, проходящей вдоль линии L.

Рис. 4.3. Поверхностные годографы:а — фиксирование поля времен поверхностным годографом; б — карта изохрон; в — трехмерное изображение поверхностного и линейного годографов

Большей частью в сейсморазведке используют прямолинейные линии наблюдения (профили). При этом различают продольные годографы, когда источники расположены на линии наблюдения, и непродольные годографы в противном случае. Если линией наблюдения является ствол скважины, то говорят о вертикальном годографе, который может быть продольным или непродольным в зависимости от расположения источника возле устья исследуемой скважины или в стороне от нее, соответственно.

Пара годографов ОТВ, полученных на одном интервале профиля при источниках, расположенных по разные стороны от него, называется встречными годографами. Если оба источника расположены по одну сторону от интервала наблюдений, то полученные годографы называют нагоняющим и нагоняемым — для дальнего и ближнего источника соответственно.

Рассмотренные до сих пор годографы имеют общую точку (возбуждения, приема или центра дистанции), которая определена на поверхности (линии) наблюдения и никак не связана со свойствами исследуемой среды и природой наблюдаемых волн. Эти разновидности, однако, не исчерпывают все возможные типы годографов. В последнее время при обработке данных МОВ, полученных по методике многократных перекрытий в сложных структурных условиях, нашли применение сейсмограммы и годографы общей точки отражения (ОТО).

Они являются развитием концепции общей глубинной точки применительно к более сложной модели среды с наклонной отражающей границей.

Наблюдателю, находящемуся на поверхности G (или линии L), представляется, что фронт волны движется вдоль этой поверхности (или линии) с некоторой скоростью v_K, называемой кажущейся скоростью и определяемой уравнениями (2.4) и (2.6). На поверхности G (рис. 4.3, а) скорость распространения следа волны

где dn_G — элемент нормали к изохроне на поверхности G; т_с — градиент поля времен на поверхности G.

Установим связь между истинной скоростью v в некоторой точке М среды и кажущейся скоростью v_K вдоль поверхности G, проходящей через эту точку. В точке М известны два градиента: пространственный градиент grad t поля времен, совпадающий с направлением луча в точке М, и поверхностный градиент grad_c t поля изохрон на поверхности G, лежащий в плоскости, которая касается поверхности G в точке М. Обозначим через е угол выхода между сейсмическим лучом и поверхностью наблюдений в точке М. На основании известного свойства градиентов — производная в любом направлении равна проекции градиента на это направление — получим

откуда, учитывая формулы (4.6) и (4.11), найдем

cos е sin а

где а — угол падения, составляемый фронтом волны с поверхностью наблюдения или лучом с нормалью к ней. Формула (4.13) равносильна уравнению (2.7) и выражает закон кажущихся скоростей (закон Бенн- дорфа).

При наблюдении на линии L кажущаяся скорость волны вдоль нее V KL Р авна

где а’ и е — углы, составляемые лучом и фронтом волны с нормалью к линии наблюдения, соответственно.

Если на поверхности G в точке М кажущаяся скорость равна v_kC, то на линии L, лежащей на этой поверхности, в той же точке кажущаяся скорость v_kL аналогично определяется соотношением

где е’ — угол между линией наблюдения L и нормалью к изохроне на поверхности G в точке М (рис. 4.3, б).

Угол падения волны на поверхность (линию) наблюдения а(а’) по абсолютной величине варьирует в пределах 0-90°, т. е. его синус изменяется в диапазоне 0-1. Поэтому, согласно (4.13) и (4.14), имеем диапазон изменения кажущейся скорости по абсолютной величине:

v 2 + y 2 +d 2 = —-l г’ 2 +d 2 , (4.17)

где г’ — расстояние на поверхности G от точки наблюдения до эпицентра S’.

На рис. 4.4, а поверхностный годограф прямой волны изображен в двух видах — как карта изохрон и как объемная фигура. Карта изо- хрон получается сечением поля времен плоскостью G и состоит из концентрических окружностей, расстояние между которыми постепенно уменьшается по мере удаления от эпицентра S’. Объемный годограф Г_с изображен над плоскостью G в системе координат (х, у, /). Из уравнения (4.17) следует, что он имеет форму гиперболоида вращения, минимум которого расположен над эпицентром S’.

Уравнение годографа вдоль прямолинейного профиля L, заданного на плоскости G уравнением у = Ь, имеет вид

t = —-Jx 2 +b 2 +d 2 =-ylx 2 +d’ 2 , (4.18)

где d’ = -Jb 2 + d 2 — расстояние от источника S до профиля.

Рис. 4.4. Поле времен и годографы ОТВ прямой волны от источника, находящегося:а, б — внутри среды; в, г, д- на поверхности наблюдений . Минимум гиперболы расположен над точкой S», которая является проекцией источника S на линию L.

Кажущиеся скорости v_kC и v_kL на плоскости и линии наблюдения можно вычислить, используя (4.17) и (4.18):

dr	‘d‘	dx ,	‘£
=——— = v i 1 +	V_K£ = —— = v.l 1 +
dt V	L dt

Кажущаяся скорость плавно изменяется от v_K = °° в эпицентре (/ = О, х = 0) до v_K = v при неограниченном возрастании расстояния до источника (/ = °о, X = °°).

Когда источник расположен на поверхности наблюдения (d = 0), уравнение (4.17) принимает вид

т. е. поверхностный годограф представляет собой конус (рис. 4.4, в). Линейный продольный годограф (Ь = 0, d = 0) описывается уравнением

и состоит из двух ветвей — отрезков прямых, исходящих из начала координат (рис. 4.4, г). Линейный непродольный годограф в этом случае определяется уравнением

и представляет собой гиперболу, симметричную относительно точки S» (рис. 4.4, д).

· Годографы ОТВ отраженной волны от плоской границы

Рассмотрим поверхностный годограф ОТВ монотипной отраженной волны. Пусть источник S находится на горизонтальной плоскости наблюдения G (рис. 4.5, а), и отражающая плоскость R имеет истинный угол наклона падения |Л Расстояние h_s по нормали от источника до отражающей границы называется ее эхо-глубиной в точке S. Скорость распространения сейсмической волны в среде, покрывающей границу, равна v.

Расположим на плоской поверхности G прямоугольную систему координат, совместив ее начало с источником S и направив ось z вниз, а ортогональные оси х и у — произвольно. Найдем время прихода отраженной волны в некоторую точку С(х, у) на плоскости наблюдения G. Опустим из S перпендикуляр на плоскость R, который пересечет последнюю в точке А, и продлим его ниже плоскости R на величину эхо- глубины до точки S (AS = AS* = h_s). Построим плоскость, которая проходит через дистанцию SC перпендикулярно отражающей грани- 146

це R. В этой плоскости, называемой лучевой плоскостью, находятся падающий луч SB и отраженный луч ВС, где В — точка отражения. В этой же плоскости находится точка А нормального отражения, для которой совпадают траектории падающего SA и отраженного AS лучей. Из равенства прямоугольных треугольников SAB и S АВ, а также из равенства углов падения и отражения следует, что SB = S В и S* С есть прямая линия в плоскости лучей. Это означает, что реальный путь пробега волны от источника S до точки В на границе и от нее до приемника С можно заменить таким же по длине фиктивным путем

Рис. 4.5. Поверхностный годограф ОТВ отраженной волны от плоской границы в однородной среде:а — геометрические построения и гиперболоид вращения; б — карта изохрон

пробега волны из точки S* прямо к приемнику С. Точку S* называют мнимым источником. Следовательно, поле времен волны, отраженной от плоской границы, сводится к полю времен прямой волны, исходящей из мнимого источника:

Изохроны отраженной волны — семейство концентрических полусфер радиусов г = у/ с центром в точке S , поскольку они существуют только в пространстве мевду плоскостями Ли G.

Если х₀, у₀, z₀ — координаты мнимого источника S , связанные соотношением

то уравнение поверхностного годографа отраженной волны имеет вид

Поверхностный годограф ОТВ отраженной монотипной волны от плоской границы является гиперболоидом вращения, вертикальная ось t которого проходит через мнимый источник S . Здесь находится минимум годографа t(S’) = /_mjn, смещенный относительно источника S в направлении восстания отражающей границы на величину

Карта изохрон отраженной волны на поверхности G (рис. 4.5, в) представляет собой семейство концентрических окружностей радиусов г с центром S’, сближающихся по мере увеличения /, поскольку с удалением от S’ кажущаяся скорость волны стремится к своему нижнему пределу (v_K —> v).

Из треугольника SS S’ найдем горизонтальное г₀ и вертикальное z₀ смещения мнимого источника относительно истинного, а

из треугольника SS’S» — компоненты х₀ и j>₀ горизонтального смещения:

r₀ = 2h_s sin |/, z₀ = 2/ij cos |/, лг₀ =-r₀cosP, у₀ =-r₀sinP,

юскость, перпендикулярная к отражающей границе R, пересекает ее вдоль прямой EF, которую называют линией отражения. Она составляет с профилем х угол cp_v — кажущийся угол наклона (падения) по этому направлению. Истинный |/ и кажущийся cp_v углы падения связаны соотношением

Как видно, кажущийся угол падения может находиться в пределах от истинного угла падения, когда профиль ориентирован вкрест простирания, т. e._t по падению драницы (Р = 0), до нуля, когда профиль х ориентирован по ее простиранию (Р = 90°):

Из (4.27) и (4.28) получаем

В этой формуле угол ср* считается положительным в направлении падения отражающей границы.

Рассматриваемая ситуация изображена в лучевой плоскости на рис. 4.6. Здесь, наряду с геометрическими построениями, аналогич-

Рис. 4.6. Изохроны и продольные годографы ОТВ прямой и отраженной волн при плоской границе в однородной среде

ными рис. 4.5, а, показаны также изохроны прямой (падающей) и отраженной волн. Продольный годограф ОТВ отраженной волны от плоской границы в однородной среде представляет собой гиперболу, симметричную относительно вертикальной оси, проходящей через проекцию мнимого источника на профиль. Минимум годографа смещен от источника S в сторону восстания границы на величину х₀ = -2h_s sincp_v, а нормальное и минимальное времена отражений таковы:

Из сравнения (4.35) с (4.33) видно, что минимальное время линейного годографа в общем случае, когда профиль не проложен вкрест простирания границы, превышает минимальное время пространственного годографа: cosip^ > cosy, поскольку (p_v 4 — 38 )

Обратим внимание на то, что прямолинейные ветви рассмотренного ранее годографа прямой волны (4.21), имеющие v_K = v, являются асимптотами гиперболического годографа отраженной волны (4.36). Если Отражающая граница наклонена, то гШёрбола сдвинута по профилю относительно своих асимптот на величину jc₀.

В произвольной точке профиля С на удалении х от источника эхо- глубина h_c до отражающей границы равна (рис. 4.6):

Используя это соотношение, уравнение (4.34) можно представить в виде

выражающем принцип взаимности для отраженной волны: время t(x) не изменится, если поменять местами источник S и приемник С.

Обратим внимание еще на одно обстоятельство. На рис. 4.5 и 4.6 отмечена точка Л/, расположенная на профиле х в середине дистанции SC, т. е. имеющая координату х!2. Эхо-глубина границы в этой точке h_M измеряется перпендикулярным к R отрезком MN, где N — точка нормального отражения на границе в случае источника в М. Как видно, точка N не совпадает с точкой В отражения волны, исходящей из источника S и наблюдаемой в пункте приема С. Эта закономерность весьма существенна: точка нормального отражения для середины дистанции при наклонной границе всегда смещена относительно точки отражения косого луча вниз по падению границы, при- чем — тем больше, чем больше величины дистанции х, угла наклона границы (p_v и ее глубины h_M.

Когда точки наблюдения относительно близки к источнику (х sin( P „ . C0S( P.r _2 . 8Н|2ф_яС08ф* „3 ,

v 2v r„ 4v J fo v*- 1 * 1 )

Обычно достаточно ограничиться первыми тремя членами ряда, аппроксимируя гиперболический годограф квадратичной параболой. При небольших углах ф часто используют приближение

Уравнение непродолыюго годографа ОТВ отраженной волны вдоль профиля, параллельного оси у, проходящего на расстоянии х = d от источника S, получим из (4.31): гдеу- расстояние по профилю до пересечения с осью х, — кажущийся угол наклона границы вдоль оси у, определенный в соотношении

· . Непродольный годограф ОТВ отраженной волны также представляет собой гиперболу, симметричную относительно основания перпендикуляра, опущенного из источника на профиль.

· Годографы ОСТ (ОГТ) и ОТО отраженной волны

от плоской границы

Обратимся к годографам общей средней (глубинной) точки, которые находят наибольшее применение в практике современной сейсморазведки. Уравнение поверхностного годографа ОСТ (ОГТ) нетрудно получить из годографа ОТВ (4.31) путем переноса начала координат из источника S в среднюю точку М дистанции SC (рис. 4.7, а). При этом размер дистанции остается прежним, но изменяются координаты ее концов и середины: S(-xl2, -у/2), М(0, 0), С(х/2, у/2). Г одограф ОСТ должен быть определен через эхо-глубину h_M в новом начале координат М.

В общем случае, когда дистанция SC не совпадает с направлением падения границы, точка нормального отражения N смещена на плоскости границы R относительно точки нормального отражения А по координатам х и у пропорционально синусам соответствующих кажущихся углов падения. Превышение эхо-глубины границы в точке М над эхо-глубиной в точке S составляет

где х и у — расстояние по соответствующим осям между источником S и приемником С. Из этого соотношения выразим h_s через h_M, подставим в уравнение (4.31) и после элементарных выкладок получим уравнение поверхностного годографа ОСТ (ОГТ):

Рис. 4.7. Поверхностный годограф ОСТ (ОГТ) отраженной волны от плоской границы в однородной среде:а — геометрические построения и трехмерный годограф; б — карта изохрон

Здесь параметр г₀ является временем нормального отражения в средней точке М, т. е. в начале координат:

Формула (4.45) позволяет вычислить время отраженной волны для любой пары точек источник — приемник, расположенных на плоскости наблюдения симметрично относительно точки М, где известна эхо- глубина границы h_м. Как и в случае годографа ОТВ, для расчета поверхностного годографа ОСТ необходимо задать скорость v в покры-

вающей среде, угол падения границы \/ и направление ее падения относительно линии дистанции SC. Последнее задается величиной угла Р, определяющего кажущиеся углы наклона границы по координатным осям хиу согласно соотношениям (4.28) и (4.30).

Поверхностный годограф ОСТ (ОГТ) отраженной монотипной волны от плоской границы в однородной среде является эллиптическим гиперболоидом с вертикальной осью t, проходящей через общую среднюю точку М (рис. 4.7, а). На плоскости G поверхностный годограф ОСТ изображается семейством изохрон в форме концентрических эллипсов, которые постепенно сближаются между собой по мере удаления от своего центра (рис. 4.7, б). Для любой изохроны t большая полуось эллипса а, совпадающая с направлением падения границы, и малая полуось Ь, совпадающая с направлением ее простирания, определяются соотношениями

Действительно, из поверхностного годографа (4.45) легко получить частные уравнения линейных продольных годографов ОСТ по направлениям хиу, совпадающим с направлениями падения и простирания границы соответственно: при р = 0 имеем sincp_v = sinxj/, siiKp^ = 0 и получаем

что эквивалентно соотношениям (4.47) при а = х и b = у.

Поверхностному годографу ОСТ (ОГТ) свойственны следующие важные особенности по сравнению с годографом ОТВ для той же модели среды. Годограф ОСТ:

· всегда, независимо от наклона отражающей границы, имеет минимум в своей общей средней точке — /_min(x, _у) = /₀;

· инвариантен к изменению направления падения границы на противоположное — при замене в формуле (4.45) значений ц>_х и (р_у на -cp_v и -фу величина t(x, у) не изменяется;

· симметричен относительно своего центра по любому направлению, проходящему через него — при замене в формуле (4.45) значений х и у на -х и -у величина t(x, у) не изменяется, в чем проявляется принцип взаимности;

· отображает направление наклона границы конфигурацией своих эллиптических изохрон: линия падения-восстания границы совпадает с большими осями эллипсов, а угол наклона границы определяет отношение малых и больших осей эллипсов.

Рассмотрим линейный продольный годограф ОСТ в общем случае, когда линия профиля L образует с осью х угол а (рис. 4.8, а). Угол между линией падения границы и осью х, как и прежде, обозначаем р. Тогда профиль L составляет с направлением падения угол у

Дистанция I между источником S и приемником С имеет проекции х и у на соответствующие оси координат:

Рис. 4.8. Линейный продольный годограф ОСТ (ОГТ) отраженной волны: а — расположение линейного продольного профиля на плоскости наблюдений; б- сейсмические лучи и годограф

Подставляя (4.49) и (4.50) в (4.45) и учитывая (4.28) и (4.30), находим

где sin

получаем формулу продольного годдитаТВа ОСТ (ОГТ) монотипной волны, отраженной от плоской границы в однородной среде:

Годограф ОСТ — гипербола, симметричная относительно средней точки. При фиксированном значении времени t₀ нормального отражения в ней форма (крутизна) годографа определяется единственным параметром v_orr. Он имеет размерность скорости, но существенно отличается от истинной скорости: v_orT является фиктивным скоростным параметром, поскольку зависит от кажущегося угла падения границы вдоль линии наблюдения. Этот угол не превосходит истинного угла падения (cp_L 2

При горизонтальной границе v_orT = v и годограф ОСТ не отличается от годографа ОТВ: формулы (4.34) и (4.53) в этом случае идентичны, поскольку I = х.

Лучи, соответствующие годографу ОСТ, действительно отражаются от общей глубинной точки границы только в случае ее горизонтальности. При наклонной границе (cp_L * 0) точка нормального отражения N смещается по горизонтали в сторону восстания относительно средней точки М на расстояние МР = Адг₀ = h_M sin (p_L (рис. 4.8, б). Когда приемник С не совмещен с источником S (/ * 0), точка отражения Е смещается по восстанию вдоль границы R относительно точки нормального отражения N на расстояние NE = Др,:

Горизонтальное смещение точки отражения Е относительно средней точки М составляет MF = Ддг, = Ддг₀ + Др, coscp_L . При этом нормаль к отражающей границе в точке Е выходит на профиль х в точке D, которая смещена относительно средней точки М на расстояние MD = Ди,:

Как видно, при наклонной границе годографу ОСТ (ОГТ) соответствует не единая точка отражения, а некоторая отражающая площадка. Ее протяженность, согласно (4.56), пропорциональна квадрату максимальной дистанции /.

Форма годографа ОТВ определяется двумя независимыми параметрами — скоростным (v) и угловым (ф), а форма годографа ОСТ — только одним параметром — фиктивной скоростью v_orT. Это его свойство оказалось очень важным при обработке данных МОВ и способствовало широкому применению метода ОГТ в сейсморазведке.

На рис. 4.9 сопоставлены трансформации продольных годографов ОТВ и ОСТ отраженной волны при изменении угла наклона границы и фиксированной величине ее эхо-глубины в общей точке годографа. С увеличением угла наклона у годографа ОТВ возрастает смещение минимума в сторону восстания границы, у годографа ОСТ — уменьшается крутизна при неизменном положении минимума в средней точке М.

Непродольный линейный годограф ОСТ получим как сечение эллиптического гиперболоида поверхностного годографа (4.45) верти-

Рис. 4.9. Сопоставление продольных годографов при изменении наклона отражающей границы:а — годографы ОТВ; б — годографы ОСТ

кальной плоскостью, не содержащей средней точки М. В общем случае непродольный годограф ОСТ не симметричен относительно своего минимума. Симметрия имеет место лишь при ориентации непродольного профиля по простиранию или падению отражающей границы.

Рассмотрим линейный продольный годограф общей точки отражения (ОТО) от наклонной границы R, падающей вдоль профиля под углом ф и находящейся в однородной среде со скоростью v (рис. 4.10). Начало координат (х, z, t) расположим в точке О, где эхо-глубина границы А₀ и время нормального отражения от точки А равно t₀ = 2Aq / v. Горизонтальная и вертикальная координаты точки отражения составляют

Поместим источник в произвольную точку профиля S и построим траекторию луча, который отражается в той же точке А и приходит на линию наблюдения в некоторую точку С. Обозначим как x_s и х_с координаты источника и приемника, расстояние между которыми (дис-

Рис. 4.10. Линейный продольный годограф общей точки отражения (ОТО)

танция) составляет /. Из простых геометрических соотношений получим выражение для годографа ОТО:

Годограф ОТО не является строго гиперболической функцией, но обладает гиперболообразной формой, будучи симметричным относительно своего минимума, который находится в начале координат. Для каждой дистанции ее средняя точка М смещена относительно начала координат в сторону падения границы, причем — тем больше, чем больше величина дистанции /. При горизонтальной границе годограф ОТО совпадает с годографом ОСТ, и точка М располагается в начале координат. Важно отметить, что на годографе ОТО не сказывается кривизна границы, поскольку все его лучи отражаются от одной ее точки. Волны, отраженные от криволинейных границ

Годограф ОТВ приобретает более сложную форму, отличную от гиперболы, когда отражающая граница криволинейна. Рассмотрим двумерную задачу в простейшем случае: отражающая граница R представляет собой дугу окружности радиуса р, центр А которой расположен под источником S, где глубина границы равна It (рис. 4.11, а). При условии р » х уравнение годографа ОТВ отраженной волны с достаточной точностью можно представить в гиперболическом виде