- Инструменты сайта
- Основное
- Навигация
- Информация
- Действия
- Содержание
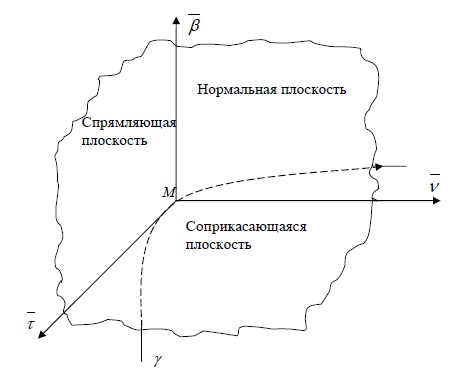
- Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
- Краткие теоретические сведения
- Кривая в пространстве
- Касательная к кривой
- Нормальная плоскость
- Соприкасающаяся плоскость
- Бинормаль и главная нормаль
- Спрямляющая плоскость
- Репер Френе
- Решение задач
- Задача 1
- Решение задачи 1
- Задача 2
- Решение задачи 2
- Задача 3
- Решение задачи 3
- Нормальная плоскость и главная нормаль кривой
- Нормальная плоскость.
- Главная нормаль.
- Кривизна и кручение пространственной кривой. Формулы Френе
- Кручение винтовой линии постоянно
- Овоаиечение:
- 🔥 Видео
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Видео:Как написать уравнения касательной и нормали | МатематикаСкачать
Касательная, нормальная плоскость, соприкасающаяся плоскость, бинормаль, главная нормаль, репер Френе
Видео:3. Геометрический смысл производной. Уравнение касательной и нормали.Скачать
Краткие теоретические сведения
Кривая в пространстве
Рассмотрим в пространстве гладкую кривую $gamma$.
Пусть точка $M$ принадлежит данной кривой и отвечает значению параметра $t=t_0$. Тогда радиус-вектор и координаты данной точки равны:
begin vec=vec(t_0), quad x_0=x(t_0),, y_0=y(t_0), , z_0=z(t_0). end
Пусть в точке $M$ $ vec(t_0)neqvec$, то есть $M$ не является особой точкой.
Касательная к кривой
Касательная к кривой, проведенная в точке $M$, имеет направляющий вектор коллинеарный вектору $vec(t_0)$.
Пусть $vec$ — радиус-вектор произвольной точки касательной, тогда уравнение этой касательной имеет вид
Здесь $lambdain(-infty,+infty)$ — параметр, определяющий положение точки на касательной (то есть разным значениям $lambda$ будут соответствовать разные значения $vec$).
Если $vec=$, $M = (x(t_0), y(t_0), z(t_0))$, то можно записать уравнение касательной в каноническом виде:
Нормальная плоскость
Плоскость, проходящую через данную точку $M$ кривой $gamma$ перпендикулярно касательной в этой точке, называют нормальной плоскостью.
Пусть $vec$ — радиус-вектор произвольной точки нормальной плоскости, тогда ее уравнение можно записать в векторном виде через скалярное произведение векторов $vec-vec(t_0)$ и $vec(t_0)$:
Если расписать покоординатно, то получим следующее уравнение:
begin x'(t_0)cdot(X-x(t_0))+y'(t_0)cdot(Y-y(t_0))+z'(t_0)cdot(Z-z(t_0))=0. end
Соприкасающаяся плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ параллельно векторам $vec(t_0)$, $vec(t_0)$, когда они неколлинеарны, называют соприкасающейся плоскостью кривой.
Если $vec$ — радиус-вектор произвольной точки соприкасающейся плоскости, то ее уравнение можно записать через смешанной произведение трех компланарных векторов $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)$:
Зная координаты точки и векторов, определяющих плоскость, запишем смешанное произведение через определитель. Получим следующее уравнение соприкасающейся плоскости:
begin left| begin X-x(t_0) & Y-y(t_0) & Z-z(t_0) \ x'(t_0) & y'(t_0) & z'(t_0)\ x»(t_0) & y»(t_0) & z»(t_0) \ end right|=0 end
Бинормаль и главная нормаль
Прямая, проходящая через точку $M$ кривой $gamma$ перпендикулярно касательной к кривой в этой точке, называется нормалью.
Таких кривых можно провести бесконечно много, все они образуют нормальную плоскость. Мы выделим среди нормалей две — бинормаль и главную нормаль.
Нормаль, перпендикулярную соприкасающейся плоскости, называют бинормалью.
Нормаль, лежащую в соприкасающейся плоскости, называют главной нормалью.
Из определения бинормали (перпендикулярна касательной и перпендикулярна соприкасающейся плоскости) следует, что в качестве ее направляющего вектора мы можем взять векторное произведение $ vec(t_0)timesvec(t_0)$, тогда ее уравнение можно записать в виде:
Как и раньше, $vec$ — радиус-вектор произвольной точки бинормали. Каноническое уравнение прямой:
Из определения главной нормали (перпендикулярна касательной и перпендикулярна бинормали) следует, что в качестве ее направляющего вектора можно взять векторное произведение $vec(t_0) timesleft[vec(t_0),vec(t_0)right]$:
Уравнение в каноническом виде распишите самостоятельно.
Спрямляющая плоскость
Плоскость, проходящую через заданную точку $M$ кривой $gamma$ перпендикулярно главной нормали, называют спрямляющей плоскостью.
Другое определение: Плоскость, определяемую касательной к кривой и бинормалью в той же точке, называют спрямляющей плоскостью.
Второе определение позволяет записать уравнение спрямляющей плоскости через смешанное произведение трех компланарных векторов, определяющих эту плоскость $vec-vec(t_0)$, $vec(t_0)$, $vec(t_0)timesvec(t_0)$: begin left(vec-vec(t_0),, vec(t_0),, vec(t_0)timesvec(t_0)right)=0. end Зная координаты соответствующих векторов, можно легко записать это смешанное произведение через определитель, раскрыв который, вы получите общее уравнение спрямляющей плоскости.
Репер Френе
Орт (то есть единичный вектор) касательной обозначим: $$ vec=frac<vec(t_0)><|vec(t_0)|>. $$ Орт бинормали: $$ vec=frac<vec(t_0)timesvec(t_0)><|vec(t_0)timesvec(t_0)|>. $$ Орт главной нормали: $$ vec=frac<vec(t_0) times[vec(t_0),,vec(t_0)]><|vec(t_0) times [vec(t_0),,vec(t_0)]|>. $$
Правая тройка векторов $vec$, $vec$, $vec$ называется репером Френе.
Видео:Математика Без Ху!ни. Касательная плоскость и нормаль к поверхности.Скачать
Решение задач
Задача 1
Кривая $gamma$ задана параметрически:
Точка $M$, принадлежащая кривой, соответствует значению параметра $t=0$. Записать уравнения касательной, бинормали, главной нормали, нормальной плоскости, соприкасающейся плоскости и спрямляющей плоскости, проведенных к данной кривой в точке $M$. Записать векторы репера Френе.
Решение задачи 1
Задачу можно решать разными способами, точнее в разном порядке находить уравнения прямых и плоскостей.
Начнем с производных.
begin 1cdot X+0cdot Y+1cdot (Z-1)=0,, Rightarrow ,, X+Z=1. end
begin left| begin X-0 & Y-0 & Z-1 \ 1 & 0 & 1\ 0 & 2 & 1 \ end right|=0 end Раскрываем определитель, получаем уравнение: begin -2X-Y+2Z-2=0 end
begin 1cdot X-4cdot Y-1cdot (Z-1)=0,, Rightarrow ,, X-4Y-Z+1=0. end
Поскольку направляющий вектор главной нормали у нас был найден как векторное произведение направляющих векторов касательной и бинормали, тройка $vec$, $vec$, $vec$ не будет правой (по определению векторного произведения вектор $vectimesvec$ направлен так, что тройка векторов $vec$, $vec$, $vec=vectimesvec$
— правая). Изменим направление одного из векторов. Например, пусть
Теперь тройка $vec$, $vec$, $vec<tilde>$ образует репер Френе для кривой $gamma$ в точке $M$.
Задача 2
Написать уравнение соприкасающейся плоскости к кривой $$ x=t,,, y=frac,,, z=frac, $$ проходящей через точку $N(0,0,9)$.
Решение задачи 2
Нетрудно заметить, что точка $N$ не принадлежит заданной кривой $gamma$. Следовательно соприкасающаяся плоскость проведена в какой-то точке $M(t=t_0)ingamma$, но при этом плоскость проходит через заданную точку $N(0,0,9)$.
Найдем значение параметра $t_0$.
Для этого запишем уравнение соприкасающейся плоскости, проведенной в произвольной точке $M(t=t_0)$. И учтем, что координаты $N$ должны удовлетворять полученному уравнению.
Соприкасающаяся плоскость определяется векторами $vec(t_0)$, $vec(t_0)$, поэтому записываем определитель begin left| begin X-t_0 & Y-t_0^2/2 & Z-t_0^3/3 \ &&\ 1 & t_0 & t^2_0 \ &&\ 0 & 1 & 2t_0 end right|=0 quad Rightarrow end
begin (X-t_0)cdot t_0^2 — (Y-t_0^2/2)cdot 2t_0 + (Z-t_0^3/3)=0. end Подставляем вместо $X$, $Y$, $Z$ координаты точки $N$: $X=0$, $Y=0$, $Z=9$, упрощаем и получаем уравнение относительно $t_0$: begin 9-t_0^3/3=0 quad Rightarrow quad t_0=3. end Подставив найденное $t_0$ в записанное ранее уравнение, запишем искомое уравнение соприкасающейся плоскости: $$ 9X-6Y+Z-9=0. $$
Задача 3
Через точку $Pleft(-frac45,1,2right)$ провести плоскость, являющуюся спрямляющей для кривой: $$ x=t^2,,, y=1+t,,, z=2t. $$
Решение задачи 3
Как и в предыдущей задаче нам неизвестны координаты точки, в которой проведена спрямляющая плоскость к заданной кривой. Найдем их.
Спрямляющая плоскость определяется касательной и бинормалью, то есть векторами $vec(t_0)$ и $vec(t_0)timesvec(t_0)$.
Записываем уравнение спрямляющей плоскости: begin left| begin X-t_0^2 & Y-1-t_0 & Z-2t_0 \ 2t_0 & 1 & 2\ 0 & 4 & -2 end right|= 0 end
Раскрываем определитель. Подставляем в уравнение координаты точки $P$: $X=-4/5$, $Y=1$, $Z=2$. Упрощаем и получаем уравнение для нахождения $t_0$: begin 5t_0^2-8t_0-4=0 ,, Rightarrow ,, t_=2,, t_=-frac25. end
Уравнения соприкасающихся плоскостей к заданной кривой, проходящих через $P$, принимают вид: begin & 5X-4Y-8Z+24=0,\ & 25X+4Y+8Z=0. end
Видео:5. Нормальное уравнение плоскости выводСкачать
Нормальная плоскость и главная нормаль кривой
Видео:Математика без Ху!ни. Уравнение плоскости.Скачать
Нормальная плоскость.
Плоскость (mathcal
), проходящую через точку (M_) кривой (Gamma) и перпендикулярную касательной к этой кривой в точке (M_), называют нормальной плоскостью кривой (Gamma) в точке (M_).
Рис. 22.5
Если кривая (Gamma) задана уравнением в векторной форме
$$
Gamma=<textbf=textbf(t), alphaleq tleqbeta>,label
$$
где
$$
textbf=(x,y,z),quad textbf(t)=(x(t),y(t),z(t)),nonumber
$$
(t_in[alpha,beta]), (overrightarrow=textbf(t_0)) и (textbf'(t_0)neq 0), то вектор (textbf'(t_0)) параллелен касательной к кривой (Gamma) в точке (M_). Пусть (M) — произвольная точка нормальной плоскости (mathcal
) (рис. 22.5), (overrightarrow=textbf). Тогда вектор (overrightarrow_=textbf-textbf(t_0)) перпендикулярен вектору (textbf'(t_)), и поэтому уравнение нормальной плоскости (mathcal
) к кривой (Gamma) в точке (M_) можно записать в виде
$$
(textbf-textbf(t_),textbf'(t_))=0nonumber
$$
или
$$
(x-x(t_))x'(t_0)+(y-y(t_))y'(t_)+(z-z(t_0))z'(t_0)=0.nonumber
$$
Видео:Математика без Ху!ни. Уравнения прямой. Часть 1. Уравнение с угловым коэффициентом.Скачать
Главная нормаль.
Любую прямую, лежащую в нормальной плоскости (mathcal
) к кривой (Gamma) в точке (M_), называют нормалью кривой (Gamma) в точке (M_). Среди всех нормалей выделяют одну — главную нормаль.
Понятие главной нормали требует введения дополнительных ограничений на вектор-функции, с помощью которых записываются уравнения кривых. Пусть (Gamma) — гладкая кривая, заданная уравнением eqref, причем для всех (tin[alpha,beta]) существует (textbf″(t)). В этом случае говорят, (Gamma) — дважды дифференцируемая кривая без особых точек.
Если (Gamma) — дважды дифференцируемая кривая без особых точек, заданная уравнением eqref, (s) — переменная длина дуги кривой (Gamma), то существуют (displaystyle frac<dtextbf>) и (displaystyle frac<d^textbf><ds^>) и справедливы равенства
$$
frac<dtextbf>=frac<textbf'(t)>,label
$$
$$
frac<d^rtextbf><ds^>=frac<s'(t)textbf″(t)-s″(t)textbf'(t)><(s(t))^>.label
$$
(circ) Применяя правило дифференцирования вектор-функции при замене переменного, получаем формулу eqref:
$$
frac<dtextbf>=frac<dtextbf>
$$
Используя формулу eqref и правило дифференцирования произведения векторной функции на скалярную, находим
$$
frac<d^textbf><ds^>=frac
$$
откуда следует формула eqref.
Перейдем к определению главной нормали. Будем считать, что (Gamma) — дважды дифференцируемая кривая без особых точек, заданная уравнением eqref. Тогда существуют (displaystyle frac<dtextbf>) и (displaystylefrac<d^textbf><ds^>), причем (displaystyle frac<dtextbf>) — единичный вектор в силу данного утверждения. Обозначим этот вектор буквой (tau). Тогда
$$
frac<dtextbf>=tau,quad |tau|=1,label
$$
и поэтому (см. данный пример) вектор (displaystyle frac=frac<d^textbf><ds^>) ортогонален вектору (tau).
Пусть (nu) — единичный вектор, параллельный вектору (displaystyle frac). Тогда
$$
frac=knu,quad|nu|=1,label
$$
причем вектор (nu) ортогонален вектору (tau).
Так как вектор (tau=displaystyle frac<dtextbf>) параллелен вектору касательной (r'(t)) к кривой (Gamma) в силу равенства eqref, то из eqref следует, что вектор (nu) параллелен нормальной плоскости кривой (Gamma) в точке (M) ((overrightarrow=r(t))). Поэтому вектор (nu) параллелен одной из нормалей кривой (Gamma) в точке (M). Эту нормаль называют главной.
Итак, если в точке (MinGamma) выполняется условие eqref, то нормаль к кривой (Gamma) в точке (M), параллельная вектору (nu) (формула eqref), называется главной нормалью.
Видео:Математический анализ, 33 урок, Касательная плоскость и нормаль к поверхностиСкачать
Кривизна и кручение пространственной кривой. Формулы Френе
Содержание:
По этой ссылке вы найдёте полный курс лекций по математике:
Пусть 7 — регулярная кривая, Мо — точка кривой 7, П — плоскость, проходящая через касательную MoT кривой 7 в точке Мо. Пусть М — точка кривой 7, близкая к точке Мо, и Р — ортогональная проекция точки М на плоскость П (рис.31). Обозначим через h длину отрезка MP и через d — длину отрезка МоМ. Плоскость П называется соприкасающейся плоскостью кривой 7 в точке Мо, если отношение стремится к нулю при Геометрическое пояснение.
Среди всех плоскостей, проходяших через касательную к кривой в точке Мо, соприкасающаяся плоскость наиболее? есно прим ыкает к кривой в некоторой (малой) окрестности это Й точки. Пусть кривая 7 задана векторным уравнением и точка М0 кривой 7 отвечает значению to параметра. Если векторы неколлинеарны, то в точке Мо существует и притом ровно одна соприкасающаяся плоскость (рис. 32). Вектор г»(/о) Рис.32 второй производной вектора r(t) кривой лежит в соприкасающейся плоскости.
Поэтому соприкасающуюся плоскость кривой называют также плоскостью ускорений. Если кривая 7 задана в координатной форме Кривизна и кручение пространственной кривой Формулы Френе понятие гладкой поверхности Способы задания то уравнение соприкасающейся плоскости записывается в виде Нормаль кривой 7 в точке Мо, лежащая в соприкасающейся плоскости По кривой в этой точке, называется главной нормалью кривой в точке Мо, а нормаль кривой 7, перпендикулярная соприкасающейся плоскости По. называется бинормалью кривой 7 в точке Мо.
Плоскость, проходящая через касательную и бинормаль кривой 7 в точке Мо, называется спрямляющей плоскостью кривой 7 в точке Мо. Лрииар 1. Найти главную нормаль и бинормаль, соприкасающуюся и спрямляют ую плоскости аинтояой линии . Начнем с ураанаиия сопри касающейся плоскости. И МММ Так мак бинормаль перпендикулярна соприкасающейся плоскости , то ее каноничесяиа уравнения записываются следующим обр ааом:
Вычисли м теперь направляющий аактор главной нормали. Имеем Заменяя найден иый вектор на коллинеариый получаем канонические уравнения главной нормали : Наконец, — уравнение спрВмлющай плоосости , перпендикулярной главной нормали. (Первой) кривизной fcj кривой 7 в точке Мо называется предел отношения при М -» Мо, где ДА — наименьший угол между ка-сательн ыми к кривой 7 в ее точках Мо И М, а Да — длина дуги ^М0М (рис. 33).
Кривизна кривой измеряет скорость ее отклонения от касательн ой. Кривизна прямой равна нулю в каждой ее точке. /» Если — естественная параметризация кривой 7, то ее кривизна к вычисляется по формуле Вектор г»(«) называется вектором кривизны кривой. Он ортогонален единичному вектору касательной г'(«), а его длина равна кривизне кривой. .
В случае произвольной параметризации и кривизна2-регулярной кривой находится по формуле Пример 2. вектор кривизны винтовой линии Поэтому кривим винтов ой линии постол ни»: Пусть Мо — точка кривой у, отвечающая значению to естественного параметра, и — единичный вектор касательной кривой у в этой то же. Если точка Мо не является точкой распрямления кривой у» fciM/О.то формулой определен единичный вектор главной нормали кривой в этой точке.
Векторное произведение является единичным вектором бинормали кривой у (рис. 34).
В случае произвольнойпараметризаци и векторы t, п и b вычисляются по формулам Три луча, исходящие из точки М0 и имеющие направления, задаваемые векторами to, по и bo, образуют сопровождающий триэдр кривой у в точке Мо (рис. 34). Пример 3. Для винтовой линии b(,)= Обозначим через Д в наименьший угол между соприкасающимися плоскостями По и П кривой 7 в точке Мо и близкой ей точке М соответственно (этот угол совпадает с наименьшим углом ме.жду бинормалями кривой в точках А/о и М), а через Дз — длину дуги ^MqM кривой 7 (рис. 35).
Кручением к2 кривой 7 в точке М0 называется предел отношения ^ при , снабженный знаком в соответствии со следующим правилом выбора знаков: если векторы сонаправлены (они всегда коллинеарны), то выбирается знак (вращение соприкасающейся плоскости происходит от вектора п к вектору если векторы ип противоположно направлены, то выбирается знак « + » (вращение соприкасающейся плоскости происходит от вектора b к вектору п) (рис. 36).
Кручение кривой определено в любой точке 3-регулярной кривой, не являющейся точкой распрямления, и измеряет скорость отклонения кривой от соприкасающейся плоскости. Кручение плоской кривой равно нулю в каждой точке. Если Кривизна и кручение пространственной кривой Формулы Френе понятие гладкой поверхности Способы задания — естественная параметризация кривой, то ее кручение вычисляется по формуле В случае произвольной параметризации имеем Пример 4.
Возможно вам будут полезны данные страницы:
Кручение винтовой линии постоянно
Вектор Дарбу является вектором мгновенной угловой скорости сопровождающего трехгранника при движении точки по кривой с единичной скоростью. Пример 8. Вектор Дарбу винтовой линии •параллелен оси винтовой линии (рис. 37). Единичные векторы касательной главной нормали п(«) и бинормали b(e) кривой 7 и ее кривизна к(в) и кручение ki(a) в каждой точке связаны соотно шениями называемыми уравнениями Френе. «
Выберем в пространстве прямоугольную декартову координ етную систему Охух так, чтобы начало координат — точка О — совпадало с точкой Мо кривой 7, отвечающей энрч ению «о = 0 естественного параметра, а ортами координатных осей Ох, Оу и Ох были единичные векторы Раскладывая векторную функцию г(в) в окрестности точки «о = 0 по степеням * и сохраняя лишь главные члены, получимуравнения кривойблизкой кривой 7:
Где Записывая последние соотношения в координатной форме и предполагая , убеждаемся в том, что проекции кривой общий вид которой показан на.рис.38, на координатные плоскости имеют следующий вид (рис. 39): на соприкасающуюся плоскость (рис. 39 а); на спрямляющую плоскость (рис. 39 б); на нормальную плоскость (рис. 39в). §5. Понятие гладкой поверхности.
Способы задания Пусть I? — ограниченная плоская область, 0D — ее граница и I) = D U 6D — оамыка ние области Д, Введем на плоскости координатную систему (u, v) и зададим на множестве Ъ три непрерывные функции с Пусть ж прямоугольные декартовы координаты точек в трехмерном евклидовом пространстве R3.
| Предположим, что функции (1) |
обладают следующим свойством: Сюйстю А. Если — различные точки множества!?» тоточки пространства R1, координаты которых вычисляются по формулам также различны. Определение. Множество 5 точек Af, координаты у и * которых определяются соотношениями (1) и функции ) обладают свойством А, называется простой поверхностью (рис. Множество точек М с координатами , — образ границы QD области D — называется границей простой поверхности 5.
Овоаиечение:
Соотношения (1) называются параметрическими уравнениями простой поверхно- сти. . Пример 1. График непрерывной функции является примером простой поверхности (рис. 41). Ее параметрические уравнения имеют вид одеФяап ып яктеодг — Пусть I, J и к — орты координатных осей. Тогда задание поверхности 5 при помощи фунхиий (1) равносильно заданию одной векторной функции — В этом случае говорят, что поверхность S задана векторным уравнением.
Простая поверхность 5 называется гладкой в точке Мо, отвечающей значениям и параметров, если функции имеют д точке («о, ^ непрерывныепроизводные. v Точка Ма гладкой поверхности 5 называется обыкновенной, или регулярной, если В противном случае точк!» А/о называется особой. , Поверхность называется регулярной, если условие (3) выполняется в каждой ее точке. Часто условие (3) удобнее записывать в равносильной форме Пример 2.
График гладкой функции является регулярной поверхностью, так как всегда Пример 3. У конической поверхности, задаваемой уравнениями все точки, кроме точки 0(0,0,0) (при и = 0, v — 0), регулярна (рис.42). В точке О имеем Другим распространенным способом задания поверхности является неявный способ задания поверхности какмножества 5 точек М .координаты х,уиг которых обращают в тождество уравнение Кривизна и кручение пространственной кривой Формулы Френе понятие гладкой поверхности Способы задания
Если гладкая фунщия своих аргументов, причем , то поверхность 5 будет регулярной. Пример 4. Сфера является регулярной поверхностью: в каждой точке. Пусть 5 — простая поверхность, Мо и М — различные ее точки. Плоскость П, проходящая через точку Мо, называется касательной к поверхности 5 в точке Мо, если при стремлении переменной точки М к точке Мо (по произвольному закону) угол между прямой МоМ и плоскостью П сгремится к нулю (рис. 43).
Пусть — векторное уравнение регулярной поверхности 5 и М0 — точка поверхности 5, отвечающая значениях! ио и v0 параметров и и v. Вычислим векторы ru(uo, vo) и г„(и0, vo), отложим их от точен Мо и проведем через точку Мо плоскость П, содержащую эти векторы. Построенная плоскость П будет касательной плоскостью поверхности в точке М0 (рис. 44), В каждой точке регулярной поверхности существует и притом ровно одна касательная плоскость.
Прямая, проходящая через точку Мо регулярной поверхности 5 и пер-пендакулярная касательной плоскости поверхности в этой точке, называется нормалью к поверхности 5 в точке М0; — вектор нормали. Рнс. 44 Пример S. Написать уравнения касательной плоскости и нормали поверхности, заданной уравнением Вычислим вектор нормали в точке Л/о- Имеем равнение касательной плоскости поверхности в точке (х
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
🔥 Видео
Репетитор по математике ищет нормаль к плоскостиСкачать
Видеоурок "Нормальное уравнение прямой"Скачать
Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать
Геометрический смысл производной. Уравнение касательнойСкачать
Уравнение плоскости через 2 точки параллельно векторуСкачать
Видеоурок "Нормальное уравнение плоскости"Скачать
Что такое нормаль?Скачать
Уравнение плоскости. Практика. Урок 5. Геометрия 11 классСкачать
Видеоурок "Уравнение плоскости по трем точкам"Скачать
9 класс, 6 урок, Уравнение окружностиСкачать
Касательная плоскость и нормаль к поверхностиСкачать
Уравнение касательнойСкачать
Уравнения касательной плоскости и нормали к эллиптическому параболоиду (устар.)Скачать
