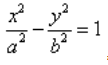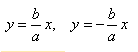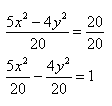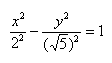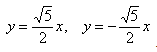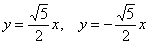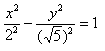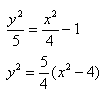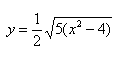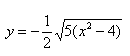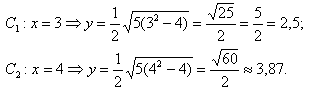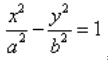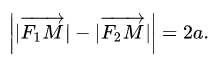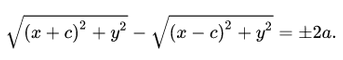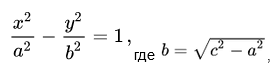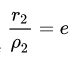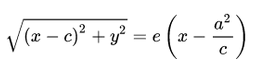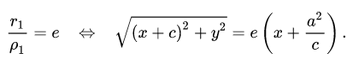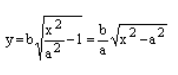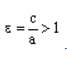Уравнение гиперболы за что отвечают коэффициенты

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value="y» data-order=»y» style=»min-width:24.3363%; width:24.3363%;»> y

<td data-cell-id="C1" data-x="2" data-y="1" data-db-index="1" data-cell-type="text" data-original-value="Расчет y» data-order=»Расчет y» style=»min-width:48.6726%; width:48.6726%;»> Расчет y0,58

<td data-cell-id="C2" data-x="2" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" / _0,5 = 8″ data-order=» 4 / _0,5 = 8″> 4 / _0,5 = 814

<td data-cell-id="C3" data-x="2" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" / ₁ = 4″ data-order=» 4 / ₁ = 4″> 4 / ₁ = 422

<td data-cell-id="C4" data-x="2" data-y="4" data-db-index="4" data-cell-type="text" data-original-value=" / ₂ = 2″ data-order=» 4 / ₂ = 2″> 4 / ₂ = 241

<td data-cell-id="C5" data-x="2" data-y="5" data-db-index="5" data-cell-type="text" data-original-value=" / ₄ = 1″ data-order=» 4 / ₄ = 1″> 4 / ₄ = 180,5

<td data-cell-id="C6" data-x="2" data-y="6" data-db-index="6" data-cell-type="text" data-original-value=" / ₈ = 0,5″ data-order=» 4 / ₈ = 0,5″> 4 / ₈ = 0,5

Теперь отмечаем найденные точки на координатной плоскости и соединяем их плавной линией, которая будет стремиться к осям координат. В итоге получится ветвь гиперболы, расположенная в первой четверти.

Чтобы построить ветвь в третьей четверти, вместо x в формулу подставляем -x. Так мы вычислим значения y.

<table data-id="196" data-view-id="196_23937" data-title="Пример значений гиперболы_2" data-currency-format="$1,000.00" data-percent-format="10.00%" data-date-format="DD.MM.YYYY" data-time-format="HH:mm" data-features="["after_table_loaded_script"]" data-search-value="" data-lightbox-img="" data-head-rows-count="1" data-pagination-length="50,100,All" data-auto-index="off" data-searching-settings="» data-lang=»default» data-override=»» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

<td data-cell-id="B1" data-x="1" data-y="1" data-db-index="1" data-cell-type="text" data-original-value="y» data-order=»y» style=»min-width:24.3363%; width:24.3363%;»> y

<td data-cell-id="C1" data-x="2" data-y="1" data-db-index="1" data-cell-type="text" data-original-value="Расчет y» data-order=»Расчет y» style=»min-width:48.6726%; width:48.6726%;»> Расчет y-0,5-8

<td data-cell-id="C2" data-x="2" data-y="2" data-db-index="2" data-cell-type="text" data-original-value=" / _-0,5 = -8″ data-order=» 4 / _-0,5 = -8″> 4 / _-0,5 = -8-1-4

<td data-cell-id="C3" data-x="2" data-y="3" data-db-index="3" data-cell-type="text" data-original-value=" / _-1 = -4″ data-order=» 4 / _-1 = -4″> 4 / _-1 = -4-2-2

<td data-cell-id="C4" data-x="2" data-y="4" data-db-index="4" data-cell-type="text" data-original-value=" / _-2 = -4″ data-order=» 4 / _-2 = -4″> 4 / _-2 = -4-4-1

<td data-cell-id="C5" data-x="2" data-y="5" data-db-index="5" data-cell-type="text" data-original-value=" / _-4 = -1″ data-order=» 4 / _-4 = -1″> 4 / _-4 = -1-8-0,5

<td data-cell-id="C6" data-x="2" data-y="6" data-db-index="6" data-cell-type="text" data-original-value=" / _-8 = -0,5″ data-order=» 4 / _-8 = -0,5″> 4 / _-8 = -0,5

Соединив полученные точки получаем следующий результат. На этом построение гиперболы завершено.

Пример 2

Рассмотренный выше пример был одним из самых простых (без смещения асимптот). Давайте усложним задачу и построим гиперболу, заданную функцией ниже:

Видео:Гипербола / влияние коэффициентов на график функцииСкачать

Что такое гипербола

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Видео:Как найти коэффициент k, если дан график гиперболы.Скачать

Понятие гиперболы

Гипербола — это множество точек на плоскости, для которых модуль разности расстояний от двух точек (они же — «фокусы») — величина постоянная и меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы в алгебре выглядит так:

, где a и b — положительные действительные числа.

Кстати, канонический значит принятый за образец.

В отличие от эллипса, здесь не соблюдается условие a > b, значит а может быть меньше b. А если a = b, то гипербола будет равносторонней.

Мы помним, что гипербола в математике выглядит так y = 1/x, что значительно отличается от канонической записи.

Вспомним особенности математической гиперболы:

• Две симметричные ветви.
• Две асимптоты. Асимптота — это прямая, которая обладает таким свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность. Их значение помогает найти специальное уравнение асимптот гиперболы.

Если гипербола задана каноническим уравнением, то асимптоты можно найти так:

Пример 1. Построить гиперболу, которая задана уравнением 5(x^2) — 4(y^2) = 20.

Приведем данное уравнение к каноническому виду (x^2)/(a^2) — (y^2)/(b^2) = 1.

Чтобы получить «единицу» в правой части, обе части исходного уравнения делим на 20:

Сокращаем обе дроби в уме или при помощи трехэтажной дроби:

Выделяем квадраты в знаменателях:

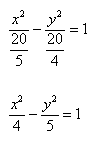
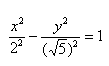
Можно было сделать проще и дроби левой части 5(x^2)/20 — 4(y^2)/20 = 1 сразу сократить и получить (x^2)/4 — (y^2)/5 = 1. Нам повезло с примером, потому что число 20 делится и на 4 и на 5. Рассмотрим пример посложнее.

Пример 2. Построить гиперболу, которая задана уравнением 3(x^2)/20 — 8(y^2)/20 = 1.

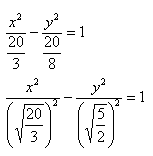
1. Произведем сокращение при помощи трехэтажной дроби:
2. Воспользуемся каноническим уравнением
   
   • Найдем асимптоты гиперболы. Вот так:
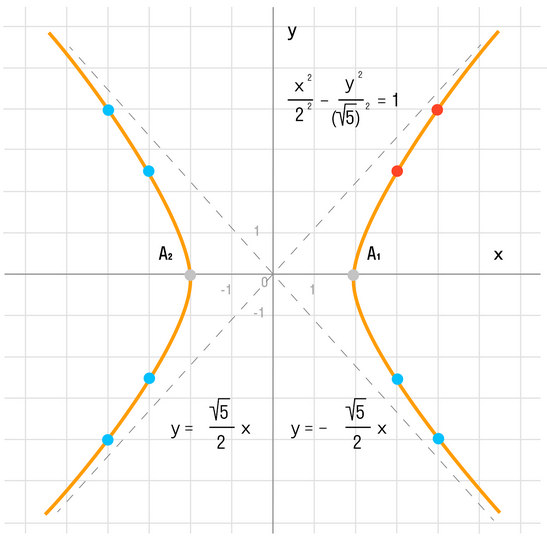
     Важно! Без этого шага ветви гиперболы «вылезут» за асимптоты.
   • Найдем две вершины гиперболы, которые расположены на оси абсцисс в точках A1(a; 0), A2(-a; 0).

Если y = 0, то каноническое уравнение (x^2)/(a^2) — (y^2)/(b^2) = 1 превращается в (x^2)/(a^2) = 1, из чего следует, что x^2 = a^2 -> x = a, x = -a.

Данная гипербола имеет вершины A1(2; 0), A2(-2; 0).

Найдем дополнительные точки — хватит двух-трех.

В каноническом положении гипербола симметрична относительно начала координат и обеих координатных осей, поэтому вычисления достаточно провести для одной координатной четверти.

Способ такой же, как при построении эллипса. Из полученного канонического уравнения

на черновике выражаем:

Уравнение распадается на две функции:

— определяет верхние дуги гиперболы (то, что ищем);

— определяет нижние дуги гиперболы.

Далее найдем точки с абсциссами x = 3, x = 4:

Может возникнуть техническая трудность с иррациональным угловым коэффициентом √5/2 ≈ 1,12, но это вполне преодолимая проблема.

Действительная ось гиперболы — отрезок А1А2.

Расстояние между вершинами — длина |A1A2| = 2a.

Действительная полуось гиперболы — число a = |OA1| = |OA2|.

Мнимая полуось гиперболы — число b.

В нашем примере: а = 2, b = √5, |А1А2| = 4. И если такую гиперболу повернуть вокруг центра симметрии или переместить, то значения не изменятся.

Видео:Определение знаков коэффициентов квадратного уравнения (параболы) по рисунку/ЗНО 2010 #25Скачать

Форма гиперболы

Повторим основные термины и узнаем, какие у гиперболы бывают формы.

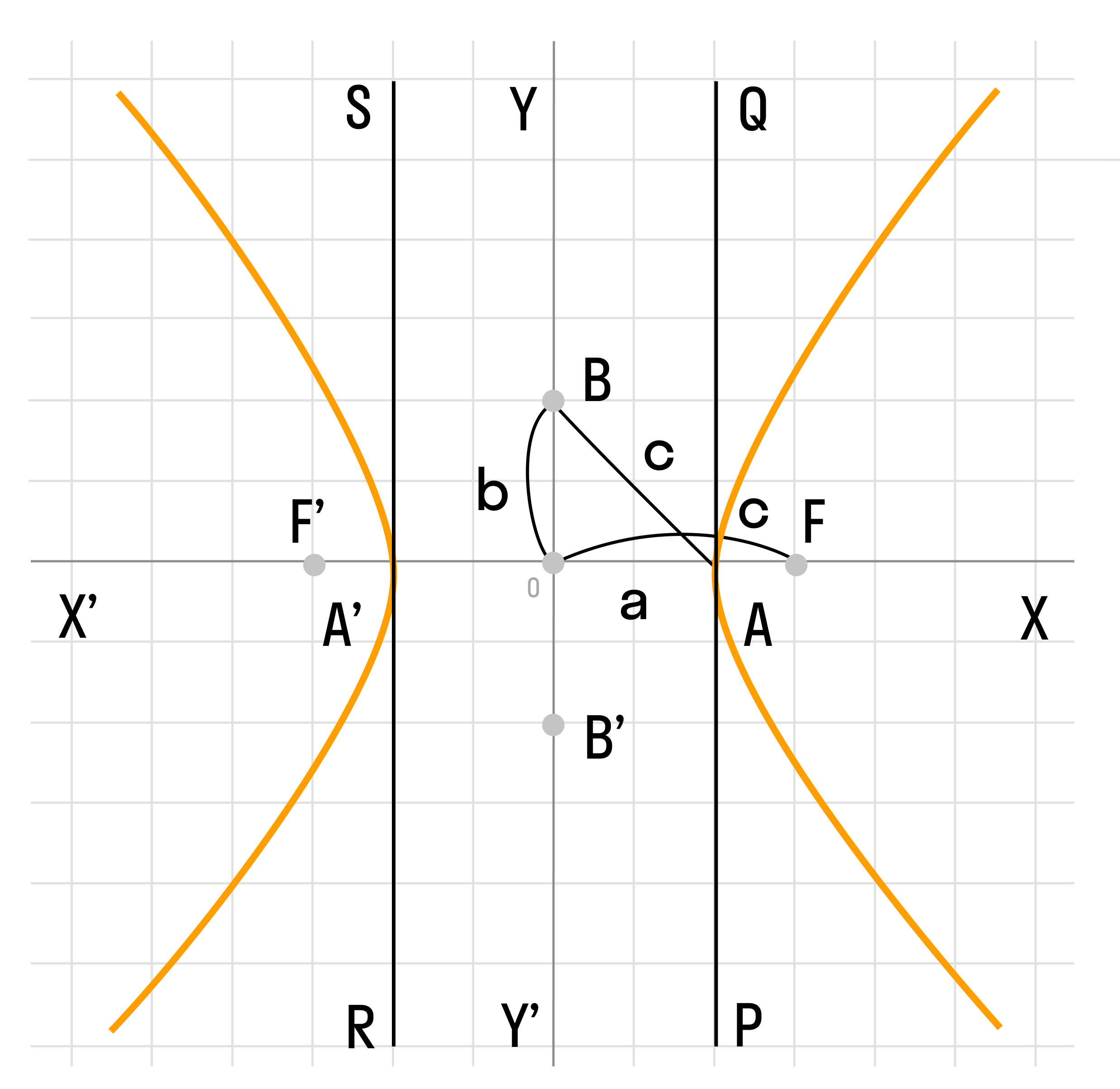
Гипербола симметрична относительно точки О — середины отрезка F’F. Она также симметрична относительно прямой F’F и прямой Y’Y, проведенной через О перпендикулярно F’F. Точка О — это центр гиперболы.

Прямая F’F пересекает гиперболу в двух точках: A (a; 0) и A’ (-a; 0). Эти точки — вершины гиперболы. Отрезок А’А = 2a — это действительная ось гиперболы.

Несмотря на то, что прямая Y’Y не пересекает гиперболу, на ней принято откладывать отрезки B’O = OB = b. Такой отрезок B’B = 2b (также и прямую Y’Y) можно назвать мнимой осью гиперболы.

Так как AB^2 = OA^2 + OB^2 = a^2 + b^2, то из равенства следует: AB = c, то есть расстояние от вершины гиперболы до конца мнимой оси равно полуфокусному расстоянию.

Мнимая ось 2b может быть больше, меньше или равна действительной оси 2а. Если действительная и мнимая оси равны (a = b) — это равносторонняя гипербола.

Отношение F’F/А’А фокусного расстояния к действительной оси называется эксцентриситетом гиперболы и обозначается e. Эксцентриситет равносторонней гиперболы равен √2.

Гипербола лежит целиком вне полосы, ограниченной прямыми PQ и RS, параллельными Y’Y и отстоящими от Y’Y на расстояние OA =A’O = a. Вправо и влево от этой полосы гипербола продолжается неограниченно.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Видео:Задание 10. ЕГЭ профиль. Гипербола. Находим коэффициенты по сдвигам.Скачать

Фокальное свойство гиперболы

Точки F1 и F2 называют фокусами гиперболы, расстояние 2c = F1F2 между ними — фокусным расстоянием, середина O отрезка F1F2 — центром гиперболы, число 2а — длиной действительной оси гиперболы (соответственно, а — действительной полуосью гиперболы).

Отрезки F1M и F2M, которые соединяют произвольную точку M гиперболы с ее фокусами, называются фокальными радиусами точки M. Отрезок, соединяющий две точки гиперболы, называется хордой гиперболы.

Отношение e = a/c, где c = √(a^2 + b^2), называется эксцентриситетом гиперболы. Из определения (2a 1 .

Геометрическое определение гиперболы, которое выражает ее фокальное свойство, аналогично ее аналитическому определению — линии, которая задана каноническим уравнением гиперболы:

Рассмотрим, как это выглядит на прямоугольной системе координат:

• пусть центр O гиперболы будет началом системы координат;
• прямую, которая проходит через фокусы (фокальную ось), примем за ось абсцисс (положительное направление на ней от точки F1 к точке F2);
• прямую, перпендикулярную оси абсцисс и проходящую через центр гиперболы, примем за ось ординат (направление на оси ординат выбирается так, чтобы прямоугольная система координат Oxy оказалась правой).

Воспользуемся геометрическим определением и составим уравнение гиперболы, которое выразит фокальное свойство. В выбранной системе координат определяем координаты фокусов F1(-c, 0) и F2(c, 0). Для произвольной точки M(x, y), принадлежащей параболе, имеем:

Запишем это уравнение в координатной форме:

Избавимся от иррациональности и придем к каноническому уравнению гиперболы:

, т.е. выбранная система координат является канонической.

Если рассуждать в обратном порядке, можно убедиться, что все точки, координаты которых удовлетворяют уравнению (x^2)/(a^2) — (y^2)/(b^2) = 1, и только они, принадлежат геометрическому месту точек, называемому гиперболой. Именно поэтому аналитическое определение гиперболы эквивалентно его геометрическому определению.

Видео:ВСЁ ПРО ГРАФИКИ ЕГЭ 2024 (Прямая, Парабола, Окружность, Модуль, Гипербола, Корень, Области, Сдвиги)Скачать

Директориальное свойство гиперболы

Директрисы гиперболы — это две прямые, которые проходят параллельно оси.

ординат канонической системы координат на одинаковом расстоянии (a^2)/c от нее. Если а = 0, гипербола вырождается в пару пересекающихся прямых, и директрисы совпадают.

Директориальное свойство гиперболы звучит так:

Гиперболу с эксцентриситетом e = 1 можно определить, как геометрическое место точек плоскости, для каждой из которых отношение расстояния до заданной точки F (фокуса) к расстоянию до заданной прямой d (директрисы), не проходящей через заданную точку, постоянно и равно эксцентриситету e.

Здесь F и d — один из фокусов гиперболы и одна из ее директрис, расположенные по одну сторону от оси ординат канонической системы координат.

На самом деле для фокуса F2 и директрисы d2 условие

можно записать в координатной форме так:

Избавляясь от иррациональности и заменяя e = a/c, c^2 — a^2 = b^2, мы придем к каноническому уравнению гиперболы. Аналогичные рассуждения можно провести для фокуса F1 и директрисы d1:

Видео:Новая задача №9 на гиперболу из ЕГЭ 2022 по математикеСкачать

Построение гиперболы

Чтобы запомнить алгоритм построения гиперболы, рассмотрим чертёж и комментарии к нему.

Построим основной прямоугольник гиперболы и проведем его диагонали. Если продолжим диагонали прямоугольника за его пределы, получим асимптоты гиперболы.

В силу симметрии достаточно построить гиперболу в первой четверти, где она является графиком функции:

Важно учесть, что данная функция возрастает на промежутке [a; ∞], при x = a, y = 0 и ее график приближается снизу к асимптоте y = (b/a) * x. Рисуем график:

Далее построенный в первой четверти график симметрично отображаем относительно оси Ох и получаем правую ветвь гиперболы. Теперь отобразим правую ветвь гиперболы относительно оси Оу.

По определению эксцентриситет гиперболы равен

Зафиксируем действительную ось 2а и начнем изменять фокусное расстояние 2с.

Так как b^2 = c^2 — a^2, то величина b изменится.

При этом ε -> 1, b -> 0 и мнимые вершины B1, B2 стремятся к началу координат, асимптоты приближаются к оси Ох. Основной прямоугольник гиперболы выражается в пределе в отрезок A1A2, а сама гипербола выражается в два луча на оси абсцисс: (-∞; -a] и [a; ∞).

При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.

При этом ε -> ∞, b -> ∞ и мнимые вершины B1B2 стремятся к бесконечности, асимптоты приближаются к оси Оу. Основной прямоугольник гиперболы вытягивается вдоль оси ординат и ветви гиперболы приближаются к прямым x = +-a и в пределе сливаются с ними. Гипербола выражается в две прямые x = +-a, которые параллельны оси Оу.

Равносторонняя гипербола это такая гипербола, у которой эксцентриситет равен √2. Ее еще называют равнобочной.

Из определения следует, что в равносторонняя гиперболе a = b, поэтому ее каноническое уравнение выглядит так: x^2 — y^2 = a^2

Действительно, ε = c/a = √2, откуда c^2 = 2a^2 и b^2 = c^2 — a^2 = a^2. И так как а и b положительные числа, получаем a = b.

Видео:Видеоурок "Гипербола"Скачать

Гипербола

Что такое гипербола? Как построить гиперболу? (Для школьников (7-11 классов)).

Функция заданная формулой (y=frac), где к неравно 0. Число k называется коэффициентом обратной пропорциональности.
Определение гиперболы.
График функции (y=frac) называют гиперболой. Где х является независимой переменной, а у — зависимой.

Что нужно знать, чтобы построить гиперболу?
Теперь обсудим свойства гиперболы:

гипербола, где k y≠0 это вторая асимптота.
И так, асимптоты x≠0 и y≠0 в данном примере совпадают с осями координат OX и OY.
k=1, значит гипербола будет находится в первой и третьей четверти. k всегда находится в числители.
Построим примерный график гиперболы.

Пример №2:
$$y=frac-1$$
Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому х+2 неравен 0.
х+2≠0
х≠-2 это первая асимптота

Находим вторую асимптоту.

Дробь (color <frac>) отбрасываем
Остается y≠ -1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-2 и y≠-1):

Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому 1+х неравен 0.
1+х≠0
х≠-1 это первая асимптота.

Находим вторую асимптоту.

Остается y≠1 это вторая асимптота.

Строим примерный график, отмечаем асимптоты (красным проведены прямые х≠-1 и y≠1):

3. У гиперболы есть центр симметрии относительно начала координат. Рассмотрим на примере:

Возьмем точку А(1;1) с координатами, которая находится на графике у=1/х. На этом же графике лежит точка B(-1;-1). Видно, что точка А симметрична точке В относительна начала координат.

4. Оси симметрии гиперболы. У гиперболы две оси симметрии. Рассмотрим пример:

Первой осью симметрии является прямая y=x. Посмотрим точки (0,5;2) и (2;0,5) и еще точки (-0,5;-2) и (-2;-0,5). Эти точки расположены по разные стороны данной прямой, но на равных расстояниях от нее, они симметричны относительно этой прямой.

Вторая ось симметрии это прямая y=-x.

5. Гипербола нечетная функция.

6. Область определения гиперболы и область значения гиперболы. Область определения смотрим по оси х. Область значения смотрим по оси у. Рассмотрим на примере:

а) Находим первую асимптоту.
Знаменатель не может равняться 0, потому что на 0 делить нельзя, поэтому x-1 неравен 0.
x-1≠0
х≠1 это первая асимптота.

Находим вторую асимптоту.

Остается y≠ -1 это вторая асимптота.

б) k=-1, значит ветви гиперболы будут находится во второй и четвертой четверти.

в) Возьмем несколько дополнительных точек и отметим их на графике.
х=0 y=0
x=-1 y=-0,5
x=2 y=-2
x=3 y=-1,5

г) Область определения смотрим по оси х. Графика гиперболы не существует по асимптоте х≠1, поэтому область определения будет находится
х ∈ (-∞;1)U(1;+∞).

д) Область значения смотрим по оси y. График гиперболы не существует по асимптоте y≠ -1, поэтому область значения будет находится
y ∈ (-∞;-1)U(-1;+∞).

е) функция возрастает на промежутке x ∈ (-∞;1)U(1;+∞).

7. Убывание и возрастание функции гиперболы. Если k>0, функция убывающая. Если k Category: 8 класс, База знаний, Уроки Tag: Гипербола Leave a comment

🎬 Видео

ИССЛЕДОВАНИЕ ГИПЕРБОЛЫСкачать

Задание 10. ЕГЭ профиль. Горизонтальные и вертикальные асимптоты гиперболы.Скачать

Парабола / квадратичная функция / влияние коэффициентовСкачать

Гипербола. Функция k/x и её графикСкачать

ГРАФИК ГИПЕРБОЛА 👌 | y = k/x | ЗАЧЕМ КОЭФФИЦИЕНТ k? #математика #гиперболаСкачать

Гипербола и ее свойства - bezbotvyСкачать

ОГЭ 2022. Задание 11. Сопоставить функции и графики. Обратная пропорциональность. ГиперболаСкачать

Задание 10 Квадратичная функция Знаки коэффициентов а и сСкачать

Графики функций. Задание №11 | Математика ОГЭ 2023 | УмскулСкачать

Как легко составить уравнение параболы из графикаСкачать

Линейная функция: краткие ответы на важные вопросы | Математика | TutorOnlineСкачать

Как отличить параболу от гиперболы?! 🙃Скачать