Уравнение гиперболы имеет вид x2 9 y2 16 1 (2 видео)

Задача 28927 4.3.81) Найти расстояние между точками.

Содержание

Условие
Решение
Дана гипербола: x2/16-y2/9=1 . Уравнения ее асимптот имеют вид (*ответ*)
Курсовая работа
📺 Видео

Условие

4.3.81) Найти расстояние между точками пересечения асимптот гиперболы
9х^2-16у^2 = 144 с окружностью, имеющей центр в правом фокусе гиперболы и проходящей через начало координат.

Решение

Канонический вид гиперболы:
(x^2/a^2)-(y^2/b^2)=1

[b] Уравнения асимптот гиперболы имеют вид:[/b]

[b]Фокусы гиперболы имеют координаты
F_(1)(-с;0) и F_(2)(с;0)
b^2=c^2-a^2[/b]

Разделим обе части уравнения на 144:
(9x^2/144)-(16у^2/144)=1
Канонический вид гиперболы:
(x^2/16)-(y^2/9)=1
a^2=16
b^2=9
Тогда
[b] уравнения асимптот гиперболы

c^2=b^2+a^2=9+16=25
[b]Фокусы гиперболы имеют координаты
F_(1)(-5;0) и F_(2)(5;0) [/b]

Уравнение окружности с центром в точке
F_(2) (5;0) и радиусом R=5 имеет вид

Чтобы найти точки пересечения гиперболы
асимптоты y=(-3/4)x
и
окружности
(x-5)^2+y^2=25
решим систему уравнений:

Подставим y=(-3/4)x во второе уравнение
(х-5)^2+((-3/4)x)^2 = 25;

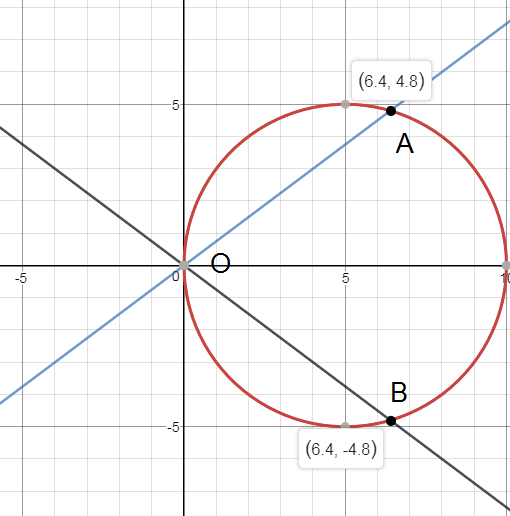
Итак, асимптота y=(-3/4)x пересекается с окружностью
(х-5)^2+y^2=25 в точках
O(0;0) и А(6,4; — 4,8)
Аналогично, асимптота y=(3/4)x пересекается с окружностью (х-5)^2+y^2=25 в точках
O(0;0) и B(6,4; + 4,8)

О т в е т. 8; 9,6

Видео:Математический анализ, 15 урок, АссимптотыСкачать

Дана гипербола: x2/16-y2/9=1 . Уравнения ее асимптот имеют вид
(ответ)

Дана гипербола: x2/16-y2/9=1 . Уравнения ее асимптот имеют вид
(*ответ*) y=-(3/4)х; y=(3/4)х
nbsp;y=-(4/5)х; y=(4/5)х
nbsp;y=-(3/5)х; y=(3/5)х
nbsp;y=-(4/3)х; y=(4/3)х
Дана гипербола: x2/16-y2/9=1. Координаты ее вершин (А1 и А2) и эксцентриситет :
(*ответ*) А1 (-4;0), А2(4;0), nbsp;=5/4
nbsp;А1 (-3;0), А2(3;0), nbsp;=4/5
nbsp;А1 (-5;0), А2(5;0), nbsp;=3/4
nbsp;А1 (0;4), А2(0;4), nbsp;=3/5
Дана гипербола: x2/9-y2/16=1. Координаты ее трюков
(*ответ*) F1(-5;0); F2(5;0)
nbsp;F1(-3;0); F2(3;0)
nbsp;F1(-4;0); F2(4;0)
nbsp;F1(0;-5); F2(0;5)
Дана парабола y2=4x. Координаты ее фокуса F и уравнение директрисы
(*ответ*) F(1;0), х=-1
nbsp;F(4;0), х=-4
nbsp;F(2;0), х=-2
nbsp;F(-1;0), х=1
Дано каноническое уравнение прямой: (x-1)/2=(y-3)/-2=(z+4)/3. Направляющий вектор nbsp;для этой прямой имеет координаты
(*ответ*) nbsp;2;-2;3
nbsp;nbsp;-1/2;3/2;4/3
nbsp;nbsp;1;3;-4
nbsp;nbsp;-1;-3;4
Дано уравнение полосы (х2 + у2)2 = 4ху. В полярных координатах оно имеет вид:
(*ответ*) r2 = 2 sin2
nbsp;r2 = 2 cos2
nbsp;r3 = 2 sin
nbsp;r2 = 4 sin2
Дано уравнение полосы (х2 + у2)2= 3х. В полярных координатах оно имеет вид:
(*ответ*) r3 = 3 cos
nbsp;r4 = 3 sin
nbsp;r4 = 3 cos
nbsp;r3 = 3 sin
Дано уравнение окружности (х — 3)2 + (у — 2)2 = 16. Общее уравнение ее горизонтального диаметра будет
(*ответ*) у — 2 = 0
nbsp;х = -3
nbsp;у = -2
nbsp;х — 3 = 0
Дано уравнение окружности х2 + (у + 3)2 = 25. Уравнение ее вертикального поперечника будет
(*ответ*) х = 0
nbsp;х = -3
nbsp;у = 3
nbsp;у = -3
Дано уравнение окружности х2 + (у + 5)2 = 4. Касательной к окружности будет ровная
(*ответ*) х = 2
nbsp;у = -5
nbsp;х = -5
nbsp;х = 0
Дано уравнение окружности: (x-1)2+(y+3)2=16. Ее радиус R и координаты центра С одинаковы
(*ответ*) R=4, C(1;-3)
nbsp;R=4, C(0;0)
nbsp;R=4, C(-1;3)
nbsp;R=16, C(1;-3)
Дано уравнение окружности: x2+(y-2)2=25. Уравнение прямой, проходящей через ее центр параллельно прямой x-y+3=0, имеет вид
(*ответ*) x-y+2=0
nbsp;x-y-5=0
nbsp;x+y+2=0
nbsp;x-y-2=0

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

Курсовая работа

Пример. На правой ветви гиперболы х 2 /16 — y 2 /9 = 1 найти точку, расстояние которой от правого фокуса в два раза меньше её расстояния от левого фокуса.

Решение: Для правой ветви гиперболы фокальные радиусы — векторы определяются по формулам r 1 = ex- а и r 2 = ex + а. Следовательно, имеем уравнение ех + а = 2(ех — а), откуда х = 3а /e; здесь а = 4, е = с /a = , т.е. х = 9,6

Ординату находим из уравнения гиперболы:

Таким образом, условию задачи удовлетворяют две точки: М 1 (9,6;0,6 ) и М 2 (9,6;-0,6 ).

Эксцентриситет гиперболы равен . Составить простейшее уравнение гиперболы, проходящей через точку М( ). [an error occurred while processing this directive]

Решение: Согласно определению эксцентриситета, имеем c/a = , или с 2 = 2а 2 . Но с 2 = а 2 + b 2 ; следовательно а 2 + b 2 = 2а 2 , или а 2 = b 2 , т.е. гипербола равнобочная.

Другое равенство получим из условия нахождения точки М на гиперболе, т.е. ( ) 2 /a 2 — ( ) 2 /b 2 = 1, или 3/a 2 — 2/b 2 = 1. Поскольку а 2 = b 2 , получим 3/a 2 — 2/а 2 = 1, т.е. a 2 = 1.

Таким образом, уравнение искомой гиперболы имеет вид х 2 — у 2 = 1.

Парабола — геометрическое место точек, равноудаленных от фиксированной точки (фокуса параболы) и фиксированной прямой (директрисы параболы). Эта фигура обладает одной осью симметрии. Если директриса параболы перпендикулярна оси О х , то уравнение кривой имеет вид (у – у 0 ) 2 = 2р(х – х 0 ),где р — расстояние от фокуса до директрисы. Уравнение директрисы x=x 0 -p/2

Начертим параболу у 2 = 8х.
Сравнивая данное уравнение с уравнением параболы видим, что 2р=8, р=4, х 0 =0, у 0 =0.

Уравнение директрисы будет x=-p/2, то есть х=-2. Координаты фокуса F(x 0 +p/2,y 0 ) то есть , F(2,0).