Уравнение гиперболического параболоида в пространстве

Видео:Построение гиперболического параболоидаСкачать

Поверхности второго порядка. Гиперболический параболоид.

Свойства гиперболического параболоида.

1. Гиперболический параболоид – неограниченная поверхность, поскольку из его уравнения следует,

что z – любое число.

2. Гиперболический параболоид обладает:

• осевой симметрией относительно оси Oz,

• плоскостной симметрией относительно координатных плоскостей Oxz и Oyz.

3. В сечении гиперболического параболоида плоскостью, ортогональной оси координат Oz, получается

4. Гиперболический параболоид может быть получен поступательным перемещением в пространстве

параболы так, что ее вершина перемещается вдоль другой параболы, ось которой параллельна оси первой

параболы, а ветви направлены противоположно, причем их плоскости взаимно перпендикулярны.

Уравнение гиперболического параболоида имеет вид:

Пересечение гиперболического параболоида с плоскостью z=z₀ является гиперболой.

Пересечение гиперболического параболоида с плоскостью x=x₀ или y=y₀ является параболой.

Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».

Видео:Аналитическая геометрия, 8 урок, Поверхности второго порядкаСкачать

Гиперболический параболоид: определение, свойства и примеры

Гиперболический параболоид: определение, свойства и примеры — Наука

Видео:Поверхности второго порядкаСкачать

Содержание:

А гиперболический параболоид — поверхность, общее уравнение которой в декартовых координатах (x, y, z) удовлетворяет следующему уравнению:

(за) 2 — (г / б) 2 — г = 0.

Название «параболоид» происходит от того факта, что переменная z зависит от квадратов переменных x и y. В то время как прилагательное «гиперболический» связано с тем, что при фиксированных значениях z мы имеем уравнение гиперболы. По форме эта поверхность похожа на конское седло.

Видео:Поверхности 2-го порядка | Лекция 14 | ЛинАл | СтримСкачать

Описание гиперболического параболоида

Чтобы понять природу гиперболического параболоида, будет проведен следующий анализ:

1.- Мы возьмем частный случай a = 1, b = 1, то есть декартово уравнение параболоида остается как z = x 2 — Y 2 .

2.- Плоскости считаются параллельными плоскости ZX, то есть y = ctte.

3.- При y = ctte остается z = x 2 — C, которые представляют параболы с ветвями вверх и вершиной ниже плоскости XY.

4.- При x = ctte остается z = C — y 2 , которые представляют собой параболы с ветвями вниз и вершиной над плоскостью XY.

5.- При z = ctte остается C = x 2 — Y 2 , которые представляют собой гиперболы в плоскостях, параллельных плоскости XY. Когда C = 0, есть две прямые (на + 45º и -45º по отношению к оси X), которые пересекаются в начале координат на плоскости XY.

Видео:6 Гиперболический параболоидСкачать

Свойства гиперболического параболоида

1.- Четыре разные точки в трехмерном пространстве определяют один и только один гиперболический параболоид.

2.- Гиперболический параболоид — это двояковыпуклая поверхность. Это означает, что, несмотря на искривленную поверхность, две разные линии проходят через каждую точку гиперболического параболоида, полностью принадлежащего гиперболическому параболоиду. Другая поверхность, которая не является плоскостью и имеет двойную линейку, — это гиперболоид вращения.

Именно второе свойство гиперболического параболоида позволило широко использовать его в архитектуре, поскольку поверхность может быть образована балками или прямыми веревками.

Второе свойство гиперболического параболоида позволяет дать ему альтернативное определение: это поверхность, которая может быть образована движущейся прямой линией, параллельной фиксированной плоскости, и разрезает две фиксированные линии, которые служат в качестве направляющих.. Следующий рисунок поясняет это альтернативное определение гиперболического параболоида:

Видео:Лекция №9. Поверхности в пространствеСкачать

Примеры работы

Видео:Математика без Ху!ни. Кривые второго порядка. Эллипс.Скачать

— Пример 1

Покажите, что уравнение:г = ху, соответствует гиперболическому параболоиду.

Видео:Лекция. Гиперболоиды, параболоиды, конус. Исследование методом сечений.Скачать

Решение

Преобразование будет применено к переменным x и y, соответствующим повороту декартовых осей относительно оси Z на + 45º. Старые координаты x и y преобразуются в новые x ‘и y’ в соответствии со следующими соотношениями:

а координата z остается прежней, т. е. z = z ‘.

Подставляя в уравнение z = x, мы имеем:

Применяя заметное произведение разницы на сумму, равную разности квадратов, мы имеем:

что явно соответствует изначально данному определению гиперболического параболоида.

Пересечение плоскостей, параллельных оси XY, с гиперболическим параболоидом z = x и определение равносторонних гипербол, которые имеют в качестве асимптотов плоскости x = 0 и y = 0.

Видео:Эллипс, парабола и гипербола. Конические сечения | Ботай со мной #055 | Борис Трушин |Скачать

— Пример 2

Определить параметры к Y б гиперболического параболоида, проходящего через точки A (0, 0, 0); В (1, 1, 5/9); С (-2, 1, 32/9) и D (2, -1, 32/9).

Видео:Образование поверхностей перемещением кривых, 1973Скачать

Решение

По своим свойствам четыре точки в трехмерном пространстве определяют единый гиперболический параболоид. Общее уравнение:

г = (х / а) 2 — (г / б) 2

Подставляем указанные значения:

Для точки A имеем 0 = (0 / a) 2 — (0 / б) 2 , уравнение, которое удовлетворяется при любых значениях параметров a и b.

Подставляя точку B, получаем:

5/9 = 1 / год 2 — 1 млрд 2

А для пункта C остается:

32/9 = 4 / год 2 — 1 млрд 2

Наконец, для точки D получаем:

32/9 = 4 / год 2 — 1 млрд 2

Что идентично предыдущему уравнению. В конечном итоге необходимо решить систему уравнений:

5/9 = 1 / год 2 — 1 млрд 2

32/9 = 4 / год 2 — 1 млрд 2

Вычитание второго уравнения из первого дает:

27/9 = 3 / год 2 откуда следует, что a 2 = 1.

Аналогичным образом второе уравнение вычитается из четверки первого, получая:

(32-20) / 9 = 4 / а 2 — 4 / а 2 -1 млрд 2 + 4 / б 2

Что упрощается как:

12/9 = 3 / б 2 ⇒ b 2 = 9/4.

Короче говоря, гиперболический параболоид, который проходит через заданные точки A, B, C и D, имеет декартово уравнение, задаваемое следующим образом:

Видео:Математика без Ху!ни. Уравнение плоскости.Скачать

— Пример 3

Согласно свойствам гиперболического параболоида, через каждую точку параболоида проходят две прямые, которые полностью в нем содержатся. Для случая z = x ^ 2 — y ^ 2 найдите уравнение двух прямых, которые проходят через точку P (0, 1, -1), явно принадлежащих гиперболическому параболоиду, так что все точки этих прямых также принадлежат тем же.

Видео:Поверхности 2го порядка. КлассификацияСкачать

Решение

Используя замечательное произведение разности квадратов, уравнение для гиперболического параболоида можно записать так:

(х + у) (х — у) = с z (1 / с)

Где c — ненулевая константа.

Уравнение x + y = c z и уравнение x — y = 1 / c соответствуют двум плоскостям с нормальными векторами п= и м= . Векторное произведение м х п = дает нам направление линии пересечения двух плоскостей. Тогда одна из прямых, проходящих через точку P и принадлежащих гиперболическому параболоиду, имеет параметрическое уравнение:

Чтобы определить c, подставляем точку P в уравнение x + y = c z, получая:

Аналогичным образом, но учитывая уравнения (x — y = k z) и (x + y = 1 / k), мы имеем параметрическое уравнение линии:

Итак, две строки:

Они полностью содержатся в гиперболическом параболоиде z = x 2 — Y 2 проходящий через точку (0, 1, -1).

В качестве проверки предположим, что t = 1, что дает нам точку (1,2, -3) в первой строке. Вы должны проверить, находится ли он также на параболоиде z = x 2 — Y 2 :

-3 = 1 2 – 2 2 = 1 – 4 = -3

Это подтверждает, что он действительно принадлежит поверхности гиперболического параболоида.

Видео:2. Приведение уравнений второго порядка к каноническому видуСкачать

Гиперболический параболоид в архитектуре

Гиперболический параболоид использовался в архитектуре великими архитекторами-авангардистами, среди которых выделяются имена испанского архитектора Антонио Гауди (1852-1926) и, в частности, также испанского Феликса Канделы (1910-1997).

Ниже приведены некоторые работы, основанные на гиперболическом параболоиде:

-Часовня города Куэрнавака (Мексика) работы архитектора Феликса Канделы.

-Океанография Валенсии (Испания), также Феликс Кандела.

Видео:Поверхности второго порядка. Поверхности вращенияСкачать

Ссылки

1. Энциклопедия математики. Линейчатая поверхность. Получено с: encyclopediaofmath.org
2. Ллера Рубен. Гиперболический параболоид. Получено с: rubenllera.wordpress.com
3. Вайсштейн, Эрик В. «Гиперболический параболоид». Материал из MathWorld — веб-ресурса Wolfram. Получено с: mathworld.wolfram.com
4. Википедия. Параболоид. Получено с: en.wikipedia.com
5. Википедия. Параболоид. Получено с: es.wikipedia.com
6. Википедия. Рифленая поверхность. Получено с: en.wikipedia.com

Что такое белые дыры?

Хорхе Кремадес: простой юмор или банализация мачизма?

Видео:А4.6. Аналитическая геометрияСкачать

Гиперболический параболоид, уравнение гиперболического параболоида

Видео:Цилиндрические поверхностиСкачать

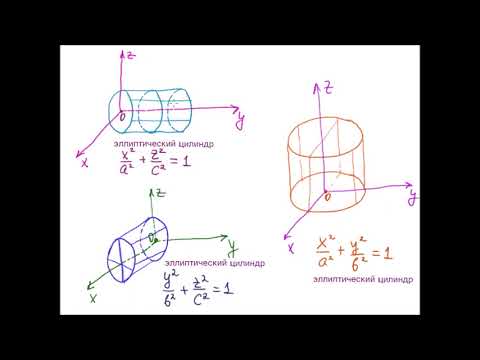
уравнение поверхности второго порядка

Поверхность, представляемая уравнением

при (p > 0, q > 0), носит название гиперболический параболоид.

Сечения плоскостями XOZ и YOZ (главные сечения — это параболы).

Параболы (2 и 3) обращены вогнутостью в противоположные стороны. Поверхность имеет седлообразный вид.

Гиперболический параболоид не имеет центра. Он симметричен относительно плоскостей XOZ и YOZ и относительно оси OZ. Прямая OZ называется осью гиперболического параболоида.

Гиперболический параболоид не является поверхностью вращения.

💥 Видео

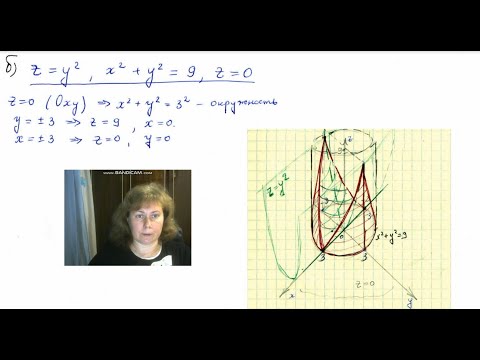
Аналитическая геометрия в пространстве Часть 2Скачать

Поверхности 2 порядкаСкачать

Математика без Ху!ни. Уравнения прямой. Часть 2. Каноническое, общее и в отрезках.Скачать

Аналитическая геометрия, 1 урок, Векторы в пространствеСкачать