Видео:Лекция 13. Энергия Гиббса и ГельмгольцаСкачать

5. Процессы. Второй закон термодинамики.
Второй закон термодинамики, в отличие от первого закона термодинамики, изучает все процессы, которые протекают в природе, и эти процессы можно классифицировать следующим образом.
Процессы бывают самопроизвольные, несамопроизвольные, равновесные, неравновесные.
Самопроизвольные процессы делятся на обратимые и необратимые. Второй закон термодинамики называют законом направленности процесса в изолированной системе (закон роста S). Слово «энтропия» создано в 1865 г. Р. Ю. Э. Клаузиусом – «тропе» с греческого означает превращение. В 1909 г. профессор П. Ауербах назвал царицей всех функций внутреннюю энергию, а S – тенью этой царицы. Энтропия – мера неупорядоченности системы.
Обратимые и необратимые процессы.
Необратимые процессы идут без затраты работы, протекают самопроизвольно лишь в одном направлении, это такие изменения состояния в изолированной системе, когда при обращении процессов свойства всей системы меняются. К ним относятся:
1) теплопроводность при конечной разности температур;
2) расширение газа при конечной разности давлений;
3) диффузия при конечной разности концентраций.
Обратимыми процессами в изолированной системе называются такие процессы, которые можно обратить без каких-либо изменений в свойствах этой системы.
Обратимые: механические процессы в системе, где отсутствует трение (идеальная жидкость, ее движение, незатухающие колебания маятника в вакууме, незатухающие электромагнитные колебания и распространение электромагнитных волн там, где нет поглощения), которые могут возвратиться в начальное состояние.
Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, Nа с большой скоростью движется по поверхности, так как идет выделение водорода проверить.).
Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.
Равновесие делится на устойчивое, неустойчивое и безразличное.
Постулаты второго закона термодинамики.
1. Постулат Клаузиуса – не может быть перехода тепла от менее нагретого к более нагретому телу.
2. Постулат Томсона – теплота наиболее холодного тела не может служить источником работы.
Теорема Карно – Клаузиуса: все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела.
Аналитические выражения второго закона термодинамики.
1. Классическое уравнение второго закона термодинамики.
Q2 / Т2 – приведенное тепло холодильника;
Q1 /Т1= Q2 /Т2 – равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.
Если делим адиабатами на множество циклов Карно, то получим.
Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.
Если процесс является конечным, то.
Это четвертое уравнение второго закона термодинамики Если процесс является замкнутым, то.
Это пятое уравнение второго закона термодинамики для обратимого процесса.
Интеграл по замкнутому контуру – интеграл Клаузиуса.
При необратимом процессе:
Это шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.
Это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.
Действие, обратное логарифму – потенцирование:
Первый закон термодинамики определяется постоянством функции U в изолированной системе. Найдем функцию, выражающую содержание второго закона, а именно, одностороннюю направленность протекающих в изолированной системе процессов. Изменение искомой функции должно иметь для всех реальных, т. е. необратимых процессов, протекающих в изолированных системах, один и тот же знак. Второй закон термодинамики в приложении к некруговым необратимым процессам должен выражатся неравенством. Вспомним Цикл Карно. Так как любой цикл можно заменить бесконечно большим числом бесконечно малых циклов Карно, то выражение:
Справедливо для любого обратимого цикла. Считая на каждом элементарном участке теплообмена Т = соnst, найдем, что:
И для всего цикла.
Энергия Гельмгольца Изохорно-изотермический потенциал.
Величина (V – ТS) является свойством системы; она называется энергией Гельмгольца. Была введена Гельмгольцем в 1882 г.
dF = dU – ТdS – SdТ,
dF = ТdS – рdV – SdТ,
F – полный дифференциал.
Увеличение объема приводит к тому, что изохорно-изотермический потенциал уменьшается (тот «минус», который стоит перед Р ). Повышение температуры приводит к тому, что F уменьшается.
Физический смысл изохорно-изотермического потенциала.
Убыль изохорно-изотермического потенциала равна максимальной работе, производимой системой в этом процессе; F – критерий направленности самопроизвольного процесса в изолированной системе. Для самопроизвольного процесса: АFТ г 0. Для равновесного процесса: ΔFТ,V = 0.
Изохорно-изотермический потенциал в самопроизвольных процессах уменьшается и, когда он достигает своего минимального значения, то наступает состояние равновесия (рис. 4).
Где 1 – самопроизвольный процесс;
2 – несамопроизвольный процесс;
3 – равновесный процесс.
Изобарно-изотермический потенциал.
1) G (Р, Т= соnst), энергия Гиббса.
G = U – ТS + РV = Н – ТS = F + РV,
Работа изобарно-изотермического процесса равна убыли изобарно-изотермического потенциала – физический смысл этой функции;
2) функция – полный дифференциал, однозначна, конечна, непрерывна.
dG = dU – ТdS – SdТ + рdv + vdр,
dG = ТdS – рdV – ТdS – SdТ + рdv + vdр,
Повышение температуры приводит к тому, что изобарно-изотермический потенциал уменьшается, так как перед S стоит знак «минус». Повышение давления приводит к тому, что изобарно-изотермический потенциал увеличивается, так как перед V стоит знак «плюс»;
3) G как критерий направленности процесса в изолированной системе.
Для самопроизвольного процесса: (ΔG)Р,Т 0. Для равновесного процесса: (ΔG)Р,Т = 0.
Изобарно-изотермический потенциал в самопроизвольных процессах уменьшается, и, когда он достигает своего минимума, то наступает состояние равновесия.
Где 1 – самопроизвольный процесс;
2 – равновесный процесс;
3 – несамопроизвольный процесс.
Совершается работа за счет ΔU и ΔН.
Противодействующие факторы. Энтальпийный фактор характеризует силу притяжения молекул. Энтропийный фактор характеризует стремление к разъединению молекул.
Энтальпия – Н Внутренняя энергия – U.
dН = dU + рdv + vdр,
dU = ТdS – SdТ + рdV + Vdр,
dН = –рdV + рdV + Vdр; U = ТdS + VdР.
Где 1 – самопроизвольный процесс,
2 – несамопроизвольный процесс,
3 – равновесный процесс,
Уравнения Гиббса – Гельмгольца – уравнения максимальной работы.
Они позволяют установить связь между максимальной работой равновесного процесса и теплотой неравновесного процесса.
Уравнение Гельмгольца (уравнение связывающее функции F и G с их температурными производными).

Уравнение Гиббса (уравнение связывающее функции F и G с их температурными производными).
Уравнения эти дают возможность рассчитать работу через температурный коэффициент функции Гельмгольца или через температурный коэффициент функции Гиббса.
Уравнение Клаузиуса-Клапейрона.
Оно позволяет применить второй закон термодинамики к фазовым переходам. Если рассчитать процессы, в которых совершается только работа расширения, то тогда изменение внутренней энергии.
Предположим, что 1 моль вещества переходит из первой фазы во вторую.
Нет условного равновесия,
Где dР/dТ – температурный коэффициент давления,
Где λфп – теплота фазового перехода.
Уравнение Клаузиуса-Клапейрона, дифференциальная форма уравнения.
Уравнение устанавливает взаимосвязь между теплотой фазового перехода, давлением, температурой и изменением молярного объема.
Эмпирическая форма уравнения Клаузиуса-Клапейрона.
Уравнение Клаузиуса-Клапейрона изучает фазовые переходы. Фазовые переходы могут быть I рода и II рода.
I рода – характеризуются равенством изобарных потенциалов и скачкообразными изменениями S и V.
II рода – характеризуются равенством изобарных потенциалов, равенством энтропий и равенством молярных объемов.
Алгебраическая сумма приведенных теплот для любого обратимого кругового процесса равна нулю.
Эта подынтегральная величина – дифференциал однозначной функции состояния. Эта новая функция была введена Клаузиусом в 1865 г. и названа энтропией – S (от греч. «превращение»).
Любая система в различном состоянии имеет вполне определенное и единственное значение энтропии, точно так же, как определенное и единственное значение Р, V, Ти других свойств.
Итак, энтропия выражается уравнением:
Где S – это функция состояний, изменение которой dSв обратимом изотермическом процессе перехода теплоты в количество Q равно приведенной теплоте процесса.
При независимых переменных U (внутренняя энергия) может обозначаться UВН и V (объем), или Р (давление) и Н(энтальпия). Энтропия является характеристической функцией. Характеристические функции – функции состояния системы, каждая из которых при использовании ее производных дает возможность выразить в явной форме другие термодинамические свойства системы. Напомним, в химической термодинамике их пять:
1) изобарно-изотермический потенциал (энергия Гиббса) при независимых переменных Т, Р и числе молей каждого из компонентов и.;
2) изохорно-изотермический потенциал (энергия Гельмгольца) при независимых переменных Т, V, ni;
3) внутренняя энергия при независимых переменных: S, V, ni;
4) энтальпия при независимых переменных: S, Р, пi;
5) энтропия при независимых переменных Н, Р, ni..
В изолированных системах (U и V= соnst) при необратимых процессах энтропия системы возрастает, dS > 0; при обратимых – не изменяется, dS = 0.
Связь энтропии с другими термодинамическими параметрами.
Для того, чтобы решить конкретную задачу, связанную с применением энтропии, надо установить зависимость между ней и другими термодинамическими параметрами. Уравнение dS = δQ/Т в сочетании с δQ = dU + РdV и δQ = dН – VdР дает уравнения:
Применительно к функциональной зависимости φ(Т, V, S) = 0, получим.
Теперь найдем зависимость энтропии от температуры из уравнений:
Вот эти зависимости:
Эти два уравнения являются практически наиболее важными частными случаями общего соотношения:
Пользуясь разными зависимостями, можно вывести другие уравнения, связывающие термодинамические параметры.
Самопроизвольные – процессы, которые идут сами собой, на них не затрачивается работа, они сами могут производить ее (движение камней в горах, натрий с большой скоростью движется по поверхности, так как идет выделение водорода), а калий буквально «прыгает» по воде.
Несамопроизвольные – процессы, которые не могут идти сами собой, на них затрачивается работа.
Равновесие делится на устойчивое, неустойчивое и безразличное.
Постулаты второго закона термодинамики.
1. Постулат Клаузиуса – «Не может быть перехода тепла от менее нагретого к более нагретому телу».
2. Постулат Томсона – «Теплота наиболее холодного тела не может служить источником работы».
Теорема Карно-Клаузиуса: «Все обратимые машины, совершающие цикл Карно с участием одного и того же нагревателя и одного и того же холодильника, имеют одинаковый коэффициент полезного действия, независимо от рода рабочего тела».
Аналитические выражения второго закона термодинамики.
1. Классическое уравнение второго закона термодинамики.
Где Q /Т – приведенное тепло;
Q2 / Т2 – приведенное тепло холодильника;
Q1 /Т1= Q2 / Т2 – равенство приведенных теплот нагревателя и холодильника. Это второе уравнение термодинамики.
Если делим адиабатами на множество циклов Карно, то получим.
Это третье уравнение второго закона термодинамики для бесконечно малого цикла Карно.
Если процесс является конечным, то.
Это четвертое уравнение второго закона термодинамики.
Если процесс является замкнутым, то.
Это пятое уравнение второго закона термодинамики для обратимого процесса.
Интеграл по замкнутому контуру – интеграл Клаузиуса.
При необратимом процессе:
Шестое уравнение второго закона термодинамики, или уравнение Клаузиуса, для обратимого процесса равно нулю, для необратимого процесса оно меньше 0, но иногда может быть больше 0.
Это седьмое уравнение второго закона термодинамики. Второй закон термодинамики – закон роста S.
Термодинамическая вероятность.
Это формула Больцмана,
Где S – энтропия – степень разупорядоченности системы;
к– постоянная Больцмана;
W – термодинамическая вероятность системы макросостояний.
Термодинамическая вероятность – число микросостояний данной системы, с помощью которых можно реализовать данное макросостояние системы (Р, Т, V).
Если W = 1, то S = 0, при температуре абсолютного нуля –273°С все виды движений прекращаются.
Термодинамическая вероятность – это число способов, которыми атомы и молекулы можно распределить в объеме.
Видео:Свободная энергия Гиббса. 10 класс.Скачать

Энергия Гиббса. Энергия Гельмгольца. Направление процесса.
Чтобы дать ответ на вопрос о возможности протекания той или иной реакции, о ее направлении и глубине необходимо снова воспользоваться II – законом термодинамики, который может быть сформулирован следующим образом: любой самопроизвольно протекающий процесс, а также и химическая реакция, идет в том направлении, которое сопровождается уменьшением свободной энергии в системе (при постоянных температуре и давлении) или энергии Гельмгольца (при постоянных температуре и объеме).
Свободная энергия или Энергия Гиббса G – это та часть всей энергии системы, которую можно использовать для совершения максимальной работы.
Энергия Гельмгольца A — это та часть внутренней энергии системы, также определяющая работоспособность и может быть применена для совершения максимальной работы.
При протекании химических реакций единовременно совершаются два направления: стремление простых частиц объединиться в более сложные, а также стремление сложных частиц к распаду на более простые.
Они не зависят друг от друга и их величины противоположны, и процесс идет в сторону той реакции, при которой изменение величины больше. Разность между этими величинами определяет свободную энергию реакции (при постоянных температуре и давлении). Ее изменение в реакции определяется разностью сумм энергий Гиббса конечных продуктов реакции и исходных веществ:
При постоянных температуре и давлении изменение энергии Гиббса связано с энтальпией и энтропией следующим выражением:
Здесь изменение энергии Гиббса учитывает одновременно изменение энергетического запаса системы и степень ее беспорядка (самопроизвольность протекания процесса).
Т.к. энергия Гиббса является мерой самопроизвольности протекания процесса, то между знаком ΔG для любой реакции и ее самопроизвольным протеканием (при постоянных температуре и давлении) существуют такие зависимости:
- Если ΔG отрицательно (ΔG 0), то реакция протекать самопроизвольно в прямом направлении не может. Однако обратная реакция идет самопроизвольно.
Энтальпийный и энтропийный факторы и направление процесса
Выясним, как функция свободной энергии зависит от изменений энтропии и энтальпии идущего процесса. Вернемся к выражению, связывающему энергию Гиббса с энтальпией и энтропией:
Без энтропийных факторов все экзотермические реакции (ΔH˂0) должны были быть самопроизвольными. Но энтропийный фактор, который определяется величиной – TΔS, может привести к росту или, наоборот, к падению способности самопроизвольного протекания.
Так, при ΔS>0, член – TΔS вносит отрицательный вклад в общую величину ΔG, следовательно он повышает возможность реакции протекать самопроизвольно.
А при при ΔS 0 Изменение энергии Гиббса. Для удобства принято сравнивать значения ΔG при стандартных условиях – концентрации равны 1 моль/л, парциальное давление газообразных веществ равно 101,3 кПа, температура 298,15 К. Тогда свободную энергию обозначают через ΔG 0 , на основе значений которой можно вычислить изменение энергии Гиббса химической реакции: Величина ΔG 0 р-ции позволяет определить, будет ли данная реакция, находящаяся в стандартных условиях, протекать самопроизвольно в прямом или обратном направлении. Аналогично теплоте образования, энергии Гиббса образования простых веществ равны нулю. Энергия Гельмгольца системы с определенной внутренней энергией (U), энтропией (S) при абсолютной температуре (Т) определяется уравнением: Изменение энергии Гельмгольца для процессов (при постоянных температуре и объеме) можно определить соотношением: ΔA — величина, которая не зависит от пути, а зависит только от исходного и конечного состояния системы, т.е. ΔA также, как и другие рассмотренные термодинамические величины, является функцией состояния. Энергия Гельмгольца подобно энергии Гиббса связана с самопроизвольностью протекания процесса. Если допустить, что система изолирована, а объем и температура постоянны, то самопроизвольно будут протекать только те процессы, при которых А уменьшается. Таким образом, при ΔA 0 – в обратном направлении, а при ΔA=0 система находится в состоянии равновесия. Энергию Гельмгольца и энергию Гиббса в стандартных состояниях можно связать с константой равновесия: Где R– универсальная газовая постоянная, K – константа равновесия, Т – абсолютная температура. Если K>>1, т.е. реакция идет в прямом направлении, то ΔG 0 ˂˂0. Если K 0 >>0 Если K=1, то ΔG 0 =0 В случае химической реакции, протекающей в гальваническом элементе при стандартных условиях ΔG 0 можно связать с ЭДС гальванического элемента следующим соотношением: ΔG 0 =-nFE 0 , где nF – количество прошедшего электричества E 0 – электродвижущая сила, при условии что все вещества, принимающие участие в реакции, находятся в стандартном состоянии. При самопроизвольном протекании процесса, его ΔG 0. Порог реакционной способности веществ для большинства реакций имеет значение ΔG 0 ≈41 кДж/моль. То есть, если ΔG 0 0 >+41 кДж/моль, то процесс неосуществим в любых реальных и стандартных условиях. Видео:Свободная энергия Гиббса и самопроизвольные реакции (видео 8) | Энергия| БиологияСкачать Функция называется характеристической, если с помощью этой функции и ее частных производных можно определить все термодина-мические свойства системы (p, V, T, S и др.) Наиболее часто употребляемыми в химической термодинамике из характеристических функций U, H, F, Z являются энергия Гиббса (G) и энергия Гельмгольца (F). Рассмотрим энергию Гиббса как функцию давления и температуры т.е. G = f (T, p). Полный дифференциал функции двух переменных можно записать как сумму частных производных этой функции по независимым переменным, умноженных на дифференциалы независимых переменных, т.е. Но из уравнения (6.123) Приравнивая коэффициенты при дифференциалах dT и dp в выражениях (6.123) и (6.126), получаем Эти выражения (6.127) показывают, что частные производные от G дают в простом и явном виде такие свойства системы как S и V. Аналогично для свободной энергии Гельмгольца, если ее рассматривать как функцию объема и температуры F = f (V,T). Сравнивая это выражение с уравнением (17), получаем Рассматривая энтальпию Н, как функцию давления и энтропии, т.е. H = f (p,S) и учитывая, что а также используя выражение (16) Аналогично для внутренней энергии U = f (S,V) С другой стороны dU = TdS – pdV. Полученные выражения (6.127)-(6.130) показывают сущность метода характеристических функций, т.е. частные производные от функции состояния системы при соответствующем выборе независимых переменных дают в простом и явном виде термодинамические параметры системы. Соотношения (6.127-6.130) имеют большое значение при решении различных физико-химических задач. Для запоминания характеристических функций можно воспользова-ться диаграммами, так называемыми мнемоническим кругом и мнемоническим квадратом, представленными на рис. 6.17. Рис. 6.17. Мнемонический квадрат и мнемонический круг для определения частных производных характеристических функций Характеристические функции F (T,V), G (T,p), H (S,p) и U (S,V) обладают следующими свойствами: а) все они являются функциями состояния, т.е. изменение этих функций при переходе системы из одного состояния в другое не зависит от пути перехода, а определяется значениями этих функций в начальном и конечном состоянии, т.е. б) функции F, G, H, U являются аддитивными, т.е. значения их зависят от размеров системы, пропорциональны числу моль или массе; в) все они имеют размерность энергии, т.е. измеряются в Дж, Дж/моль, кДж; г) физический смысл изменения характеристических функций — есть работа некоторого процесса при определенных условиях, согласно выражениям (6.114), (6.116), (6.118) и (6.119); д) при переходе системы в состояние равновесия характеристические функции принимают экстремальное значение; е) характеристические функции взаимосвязаны. Последнее свойство имеет большое значение для физико-химических исследований. Взаимосвязь функций U, F, G, H хорошо видна на диаграмме соотношений между ними (рис. 6.18) Рис. 6.18. Соотношение между характеристическими функциями На рис. 6.18 характеристические функции изображены в виде отрезков, длины которых находятся из следующих соотношений H = U + pV = G + TS = F + pV + TS F = U – TS = G – pV (6.131) G = H – TS = U + pV – TS Используя соотношения (6.131) и значения частных производных (6.127), (6.128) можно получить уравнения Гиббса-Гельмгольца, которые также отражают взаимосвязь характеристических функций. Получим уравнения Гиббса-Гельмгольца. По определению G = H – TS, (6.113), но из (6.117) имеем Подставляя (6.127) в (6.113) получаем т.е. связь таких термодинамических функций, как энергия Гиббса и энтальпия системы. Если рассматривать изменение этих функций в каком-либо процессе, то получим первое уравнение Гиббса-Гельмгольца, а именно Соотношение (6.132) устанавливает связь между тепловым эффектом химической реакции, протекающей при постоянном давлении и макси-мальной полезной работе изобарно-изотермического процесса, т.е. Аналогично для свободной энергии Гельмгольца, согласно (6.115) Подставляя (6.128) в (6.115), получаем: т.е. связь свободной энергии Гельмгольца (F) и внутренней энергии системы (U), а также Выражение (6.134) устанавливает связь между тепловым эффектом химической реакции, протекающей при постоянном объеме, и максимальной полезной работой изохорно-изотермического процесса, т.е. т.к. DU = QV, а –DF = W¢m (согласно 40) Теплоты Qp и QV в выражениях (6.133) и (6.135) относятся не к процессам, которым соответствует работа W¢m. W¢m — это работа обратимого процесса, а Qp = DH и Q = DU- тепловые эффекты химических реакций или физико-химических процессов, когда они совершаются предельно необратимо, но между теми же начальным и конечным состояниями системы. Теплоты же равновесного процесса равные Qобр = TDS, выражаются последними членами уравнений 6.132, 6.133, 6.134, 6.135. Исходя из изложенного, можно записать Уравнения 6.133 и 6.134 можно привести к виду, удобному для интегрирования. Для этого разделим обе части уравнений на Т 2 и выполним преобразования: Тогда получаем или Интегрирование уравнений (6.136) дает следующие выражения: Соотношения (6.137) позволяют вычислить максимальную полезную работу изобарического (W¢p,max) и изохорического (W¢V,max) процессов, зная его теплоту Qp или QV, если возможно найти постоянную интегрирования. Уравнения Гиббса-Гельмгольца широко используются в физико-химических расчетах, например, для вычисления тепловых эффектов химических реакций по опытным значениям электродвижущих сил электрохимических элементов, для вычисления DS и других термодинами-ческих величин. Основные понятия химического равновесия и процессы прогнозирования свойств получаемых материалов Общие соотношения, вытекающие из второго закона термодина-мики, позволяют определить условия химического равновесия. Более простым случаем является равновесие при химических реакциях, протекающих без фазовых превращений, т.е. реакциях, когда исходные вещества и продукты находятся в одной фазе. Например, реакции между газами или реакции в растворах. Химические процессы, играющие важную роль при создании материалов, как правило, не протекают до полного исчезновения исходных веществ, и останавливаются, достигая определенного состояния химии-ческого равновесия. Основной целью синтеза любого материала является максимальное достижение выхода конечных продуктов, поэтому важно уметь характе-ризовать равновесие и найти параметры, от которых оно зависит, чтобы управлять процессом в целом. Одним из важных вопросов химической термодинамики является вопрос о возможности и направленности протекания самопроизвольного процесса и условии равновесия. Возможность, направление и предел самопроизвольного протекания процессов перехода энергии или вещества от одной части системы к другой зависят только от соотношения факторов интенсивности. Такими факторами являются температура (критерий перехода теплоты), давление (критерий перехода газа), потенциал заряда (критерий перехода электричества) и т.д. Критерием самопроизвольного перехода данного компонента из одной фазы в другую является химический потенциал данного компонента, который тоже относится к факторам интенсивности. При умножении его на изменение количества этого компонента дает изменение соответствующего вида энергии. Согласно II закону термодинамики самопроизвольное протекание процессов взаимодействия между разными частями системы возможно только в направлении выравнивания фактора интенсивности (температуры, давления, химического потенциала и т.д.) для всех частей системы. Достижение одинакового значения этого фактора является пределом самопроизвольного течения процессов в данных условиях и, следовательно, условием равновесия. Так, условием равновесия между фазами a и b компонента i служит равенство химического потенциала этого компонента в обеих фазах. Этот вывод относится к любому компоненту, входящему в состав фаз, и к любым фазам системы. Таким образом, из какого бы числа компонентов и из какого бы числа фаз ни состояла гетерогенная система условием равновесия между фазами в ней является то, что химический потенциал любого данного компонента должен быть одинаковым во всех фазах системы. Химический потенциал До сих пор мы рассматривали системы, сохраняющие постоянной массу, в которых изменение энергии было следствием сообщения или отнятия теплоты или результатом совершения работы. Течение многих процессов сопровождаются изменением числа моль компонентов в системе. Так, например, любая гомогенная химическая реакция протекает с уменьшением числа моль исходных веществ и увеличением продуктов реакции, при фазовых переходах один компонент переходит из одной фазы в другую, в результате количество его уменьшается в одной фазе и увеличивается в другой. С помощью эксперимента установлено, что любое химическое изменение системы зависит от природы реагентов, состава исходных веществ и продуктов реакции, от концентрации реагентов и от внешних условий (Т, Р). А любое изменение химического состава системы с термодинамической точки зрения является результатом перераспределения масс отдельных компонентов в системе. Термодинамическое описание таких систем, в которых происходит изменение массы взятых веществ, имеет большое практическое значение. Изменение количества вещества в системе (появление или удаление его) приводит к изменению энергии системы. Допустим, что увеличивается масса одного лишь компонента на dn1, тогда внутренняя энергия (U) увеличивается на величину, пропорциональную dn1. Коэффициент пропорциональности обозначим через m (его размерность При изменении числа моль компонентов в системе внутренняя энергия будет меняться на величину mdn. Основное уравнение термодинамики с переменным составом будет выглядеть так: или DU = TDS – pDV + mDn (6.140) Решив его относительно коэффициента m получим важное соотношение: где Gm — мольное значение функции G для данного вещества, которое для чистого вещества является его химическим потенциалом. Химический потенциал вещества зависит от межмолекулярных сил в системе, а в индивидуальном веществе проявляются силы взаимодействия между одинаковыми молекулами А-А. Если система представляет смесь веществ А и В, то возможны и другие взаимодействия между молекулами А-В и В-В. Если система, в которой происходит изменение числа моль компонентов, не совершает никаких других видов работы, кроме работы расширения, то из сравнения уравнения (6.139) и уравнения: dU = TdS – pdV – dW¢max Следовательно, величина midni имеет смысл химической работы, которая совершается при протекании химической реакции. Любой вид работы можно представить в виде произведения фактора интенсивности (силы, давления, поверхностного натяжения и т.д.), не зависящего от массы, на изменение фактора экстенсивности (емкости): dWэлектрич. = – EdP (P — поляризация) dWобраз. единицы поверхности = – sdS; (где S — поверхность) Таким образом, dn — изменение фактора экстенсивности, а m — фактор интенсивности. Во всех случаях взаимодействия систем с различными потенциалами происходит их выравнивание за счет изменения соответствующих факторов емкостей. Например, давление выравнивается за счет изменения объема и т. д. Выравнивание химических потенциалов происходит за счет изменения масс веществ. Но в отличие от Р и Т, которые могут быть измерены, химический потенциал не может быть измерен непосредственно. Тем не менее, химический потенциал — важная термодинамическая функция, которую применяют для изучения равновесия в различных термодинамических системах. Понятие о химическом потенциале введено в химию Дж. Гиббсом в 1878 году. Если рассматривать смеси переменного состава и записать уравнения других термодинамических потенциалов: то из этих уравнений также следует, что химический потенциал можно выразить через любую характеристическую функцию: где ni — постоянное количество всех компонентов; nj — постоянное количество всех компонентов, кроме рассматриваемого; i ¹ j . Т.е. химический потенциал данного вещества равен частной производной от любого термодинамического потенциала по числу моль данного вещества при соответствующих условиях. Чаще всего изучаются системы при p, T = const, поэтому в дальнейшем химический потенциал i-того компонента будем определять как приращение энергии Гиббса при добавлении одного моль этого компонента к большому объему системы при постоянных температуре и давлении. Понятие «большой объем системы» означает, что состав системы практически не изменяется после добавления одного моль компонента. Как уже указывалось, химический потенциал чистого вещества равен энергии Гиббса одного моль этого вещества: mi = Gi, т.к. при изменении количества чистого вещества на один моль, энергия Гиббса изменится на величину, равную энергии Гиббса одного моль вещества. Если в системе содержится “n” моль компонента, то Итак, во всех практически важных расчетах вычисление химическо-го потенциала связано с определением функции G для изучаемой системы. Рассмотрим условия равновесия и самопроизвольности процессов, связанных с изменением состава. Запишем основное уравнение термо-динамики таких систем, когда в системе содержится k компонентов Т.к. в изобарно-изотермической системе условием самопроизвольности является dGВсегда ˂0 Реакция самопроизвольна при любых температурах, обратная реакция всегда несамопроизвольна >0 ˂0 Всегда >0 Реакция несамопроизвольна при любых температурах, обратная реакция самопроизвольна ˂0 ˂0 При низких температурах ˂0, при высоких температурах >0 Реакция самопроизвольна при низких температурах, обратная реакция становится самопроизвольной при высоких температурах >0 >0 При низких температурах >0, при высоких температурах ˂0 Реакция несамопроизвольна при низких температурах, но при высоких температурах становится самопроизвольной Характеристические функции. Уравнения Гиббса-Гельмгольца
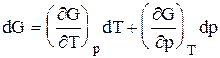


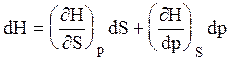







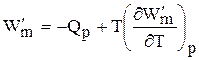




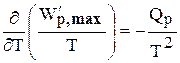



💥 Видео
Вывод формул для энергии Гельмгольца, Гиббса и энтальпии с помощью преобразования ЛежандраСкачать

Энергия ГиббсаСкачать

Энергия Гиббса и Гельмгольца.Фугитивность и активность.Термодинамические потенциалы.Скачать

2 4 Свободная энергия ГиббсаСкачать

Свободная энергия Гиббса и спонтанностьСкачать
Коробов М. В. - Физическая химия. Часть 1 - Фазовое равновесие. Уравнения Гиббса-Дюгема-МаргулесаСкачать

Успенская И. А. - Химическая термодинамика и кинетика - Функции Гиббса и ГельмгольцаСкачать

Обратимые и необратимые процессы. Энтропия. Второй закон термодинамики. 10 класс.Скачать

Химия | Тепловой эффект химической реакции (энтальпия)Скачать

Что такое Энтропия?Скачать

Энтропия. 10 класс.Скачать

Энергия Гиббса. Практическая часть. 10 класс.Скачать

Коробов М. В. - Физическая химия. Часть 1 - Характеристические функцииСкачать

Фазовые равновесия | ФизхимияСкачать
Почему энергия Гиббса так важна ?Скачать

Внутренняя энергия и энтальпия. 10 класс.Скачать

Урок 197. Поверхностная энергия. Коэффициент поверхностного натяженияСкачать


















































