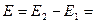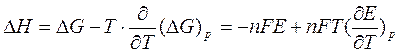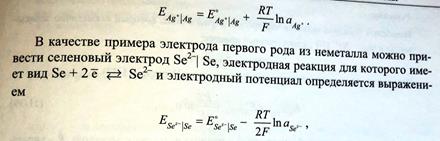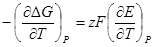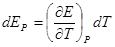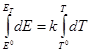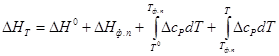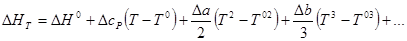Уравнение гиббса гельмгольца для равновесной электрохимической цепи

Видео:Лекция 13. Энергия Гиббса и ГельмгольцаСкачать

Правило знаков ЭДС элементов и электродных потенциалов

1. Основополагающее правило – ЭДС положительна, если внутри гальванического элемента положительное электричество (катионы) перемещается слева направо (Стокгольм, международная конференция 1953г.)

2. Выводы. При разряде ионов на правом электроде — процесс восстановления (электрод заряжается положительно), а сам электрод – положительный полюс г.э. (катод); на левом электроде – процесс окисления (отрицательный полюс, анод).

3. Соответствие знака ЭДС системе знаков теории хим. сродства а)

б) и , самопроизвольный процесс

53. Электрохимическая форма уравнения Гиббса-Гельмгольца. Зависимость ЭДС гальванического элемента от температуры. Температурный коэффициент ЭДС и его связь с энтропией химической реакции в гальваническом элементе.

Уравнение Гиббса-Гельмгольца применительно к электрохимической цепи:

Если , то химическая реакция протекающая в элементе, может быть только экзотермической;

, то реакция также может быть только экзотермическая;

, то химическая реакция в элементе может быть как экзо-, так и эндотермической.

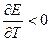
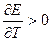
n — число электронов участвующих в электрохимической реакции;

ΔG – изменение энергии Гиббса для химической реакции, протекающей в гальваническом элементе.

Производная ΔG по температуре дает значения энтропии ΔS:

где ΔS — изменение энтропии для химической реакции, протекающей в гальваническом элементе;

— температурный коэффициент э.д.с.

Измерив э.д.с. элемента и ее температурный коэффициент, можно найти ΔG и ΔS для суммарного процесса, протекающего в элементе.

Изменение энтальпии для химической реакции в элементе вычисляют, используя уравнение Гиббса-Гельмгольца:

Классификация электродов. Окислительно-восстановительные электроды, потенциал которых не зависит от концентрации ионов водорода. Приведите пример, электродную реакцию и уравнение Нернста для расчёта потенциала электрода указанного типа.

1) Электроды 1-го рода

2) Электроды 2-го рода

3) Электроды 3-го рода

4) Газовые электроды

5) Ионоселективные электроды

6) Окислительно-восстановительные электроды

Про окислительно-восстановительные электроды см. 60.

Электроды первого рода. Примеры. Вывод и анализ уравнения, связывающего потенциал электрода с активностями потенциалопределяющих ионов.

См. п.56

Электроды первого рода, обратимые по катиону: определение, примеры, уравнение, связывающее потенциал электрода с активностями веществ, участников электродной полуреакции (уравнение Нернста). Амальгамные электроды.

Электрод первого рода – это металл (или неметалл), погруженный в раствор, содержащий ионы этого же металла (неметалла).

Таким образом, потенциал электрода первого рода определяется активностью катионов металла в растворе или активностью анионов неметалла. Ионы, от активности которых непосредственно зависит потенциал электрода, называются потенциалопределяющими.

Примерами электродов первого рода, обратимых по катиону, могут служить металлы в растворах их растворимых солей (Ag в растворе AgNO3, Cu в растворе CuSO4).

Так, для серебряного электрода Ag + |Ag электродная реакция имеет вид: Ag + +е =Ag

Электродный потенциал определяется выражением:

Приведите пример электрода второго рода. Запишите электродную реакцию и уравнение Нернста для выбранного электрода. Влияние концентрации потенциалопределяющих ионов на потенциал электрода.

Электрод второго рода – металл, покрытый слоем его малорастворимого соединения (соли/оксида/гидроксида) и погруженный в раствор электролита, который содержит тот же анион, что и малорастворимое соединение.

Таким образом, потенциал электрода второго рода определяется активностью анионов: такие электроды обратимы по аниону.

Электрод, представляющий собой ртуть, покрытую пастой из смеси каломели Hg₂Cl₂ cо ртутью, находящуюся в контакте с раствором хлорида калия: Cl — | Hg₂Cl₂|Hg, называют каломельным электродом.

Ввиду низкой растворимости каломели в воде активность хлорид-ионов считают практически равной активности хлорид-ионов, образуемых при диссоциации хлорида калия, поэтому концентрация хлорида калия в растворе должна быть точно известна. Наиболее часто используют каломельные электроды, в которых концентрация KCl отвечает насыщению (насыщенный) или равна 0,1 или 1,0 моль/л. Каломельные электроды (особенно насыщенный) удобны тем, что диффузионный потенциал, возникающий в электрохимической цепи на границе насыщенный раствор хлорида калия – данный раствор, незначителен и во многих случаях (не требующих большой точности) им можно пренебречь.

Потенциалы электродов зависят, в первую очередь, от соотношения активностей (концентраций) потенциалопределяющих ионов в растворе. Увеличение концентрации окисленной формы (или уменьшение концентрации восстановленной формы) приводит к возрастанию потенциала электрода. Вместе с тем, ионы (вещества), не участвующие в электродных реакциях (индифферентные), изменяют ионную силу раствора, а, следовательно, и коэффициент активности и активность потенциалопределяющих ионов. Это опять же приводит к изменению потенциала электрода. Те вещества, которые вступают в химическое взаимодействие с потенциалопределяющими ионами, также влияют на потенциалы электродов.

Видео:Свободная энергия Гиббса. 10 класс.Скачать

ТЕРМОДИНАМИКА ЭЛЕКТРОХИМИЧЕСКИХ СИСТЕМ

При обратимом протекании в системе какого-нибудь процесса в изотермических условиях и при постоянном давлении связь между изменением энергии Гиббса (ΔG), энтальпии (ΔН) и энтропии (ΔS) дается уравнением

в котором TΔS есть изменение связанной энергии системы. При этом система представляется настолько большой, что переход ее от начального состояния к конечному не вызовет заметного изменения параметров. Например, в системе с химической реакцией начальные и конечные концентрации участников реакции можно считать одними и теми же. Если в системе идет процесс перехода вещества от большей концентрации к меньшей, то эти изменения происходят на бесконечно малую величину и т. д. Из термодинамики известно, что

Это уравнение принято называть уравнением Гиббса — Гельм-гольца. Убыль энергии Гиббса электрохимической системы равна максимальной работе ΔА, которую может совершить система, а эта максимальная электрическая работа равна произведению напряжения системы на количество прошедшего электричества, т. е. zFE. Таким образом:

Продифференцируем это выражение по температуре:

Следовательно, изменение энтропии можно определить из температурного коэффициента напряжения системы.

Подставив в уравнение Гиббса — Гельмгольца выражение убыли энергии Гиббса, получим

Так как изотермическая и обратимая электрическая работа является полным дифференциалом параметров Р, Т, то

и если Р = const, то

и полученное уравнение переписываем в виде:

В этом уравнении ΔН относится к количеству вещества, вступившему в реакцию при прохождении zF количества электричества, т. е. к одному молю.

Совершенно аналогичное выражение получается, если процесс идет изотермически и обратимо, но не при постоянном давлении, а при постоянном объеме. Тогда

или

Электрическая работа, совершаемая системой, может быть больше, меньше или равна изменению энтальпии в зависимости от знака температурного коэффициента напряжения. Если (dE/dT)_P = 0, то

и электрическая работа точно равна изменению энтальпии. Это уравнение называется уравнением Томсона. Его иногда применяют для ориентировочных расчетов напряжения.

Если (dE/dT)_P > 0, то электрическая работа больше изменения энтальпии и электрохимическая система в обратимом изотермическом режиме превращает в электрическую работу не только энергию, выделяющуюся при уменьшении энтальпии процесса, но и часть энергии окружающей среды. В адиабатическом режиме система, следовательно, будет охлаждаться.

В качестве примеров рассмотрим несколько электрохимических систем с водными и расплавленными электролитами (табл. 6.4).

Таблица 6.4. Проверка уравнения Гиббса — Гельмгольца

Система 1 обладает отрицательным температурным коэффициентом, и реакция в ней протекает с уменьшением энтальпии (экзотермическая реакция), которая из термохимических данных в условиях протекания реакции равна — 218,0 кДж/моль. Электрическая работа, которую может совершить система, меньше, чем ΔН. Расчет по формуле дает значение изменения энтальпии системы, очень близкое к определенному из термохимических измерений. В рассматриваемой электрохимической системе 90% выделяемой теплоты расходуется на совершение электрической работы, а 10% рассеивается или нагревает систему. Аналогичные соотношения имеем и для систем 4, 5. Рассчитанные из электрохимических измерений значения энтальпии совпадают с термохимическими данными в пределах ошибок опыта, а в электрическую работу превращается соответственно 73 и 82% от выделяющейся теплоты.

Температурный коэффициент напряжения системы 2 положителен. В соответствии с этим в электрическую работу превращается не только вся теплота, выделяющаяся при протекании реакции, но и часть теплоты (примерно 33%), поглощенной из окружающей среды. Значения энтальпии, определенные из электрохимических и термохимических измерений, хорошо согласуются друг с другом.

Наконец, в электрохимической системе 3 положителен не только температурный коэффициент напряжения, но и изменение энтальпии. Следовательно, эта система отбирает тепловую энергию от внешней среды не только для совершения электрической работы, но и на химическую реакцию.

Данные, приведенные в табл. 6.4, относятся к реакциям, протекающим не при стандартной температуре (298,15 К или 25°С). Для стандартных условий уравнение Гиббса — Гельмгольца должно быть записано в виде:

Т, К	z	E, B	, В/град	ΔG,	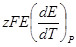,	ΔН, кДж/моль
из изме-рения напря-жения	из тер-мохи-мичес-ких данных
1,015 0,476 0,164 1,100 0,913	– 4,02∙10 –4 3,85∙10 –4 0,84∙10 –3 – 0,67∙10 –3 – 0,29∙10 –3	– 196,0 – 92,0 – 31,6 – 212,6 – 88,1	– 21,0 21,8 46,7 – 79,0 – 20,4	– 217,0 – 70,2 15,1 – 291,6 – 108,5	– 218,0 – 69,1 15,7 – 289,1 – 106,8

Здесь Е°, ΔН°, Т°, dE°/dT — величины, относящиеся к стандартным условиям.

Если же необходимо провести расчеты при каких-нибудь условиях, отличных от стандартных, то нужно знать ΔН и dE/dTдля этих условий. Рассмотрим сперва зависимости этих величин от температуры, считая, что активности участников реакции при всех температурах равны единице,

Вообще говоря, температурный коэффициент напряжения может изменяться с температурой, а также оставаться постоянным в значительном температурном интервале. Характер его изменения будет определяться изменением напряжения с температурой.

Продифференцируем уравнение Гиббса — Гельмгольца по температуре:

Из этого выражения следует, что

и если напряжение системы не зависит от температуры или линейно зависит от нее, то (∂ 2 Е/∂∂Т 2 )_Р =0 и тогда

Но в соответствии с уравнением Кирхгоффа

где 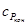и — соответственно молярные теплоемкости при постоянном давлении конечных продуктов и начальных участников протекающего процесса.

Следовательно, для соблюдения условий независимости или линейного хода Е с температурой нужно, чтобы при протеканиипроцесса не происходило бы изменения теплоемкости системы, т. е. чтобы Δс_Р = 0. Тогда изменение напряжения с температурой будет происходить только вследствие изменения энтропии системы.

В рассматриваемом случае, поскольку изменение энтальпии не зависит от температуры, можно легко определить значение Е для любой температуры (Е_т), если только линейный ход Е с температурой соблюдается вплоть до этой температуры. Из выражения

Е_т = Е 0 + k (Т – Т 0 )

где k — положительное или отрицательное значение температурного коэффициента.

Если же температурный ход напряжения системы не линейный, то напряжение системы определяется следующим образом. Определим изменение энтальпии при температуре Т(ΔН_Т) интегрированием уравнения Кирхгоффа:

В случае какого-либо фазового превращения в системе в данном интервале температур нужно учесть также изменение энтальпии при этом превращении (ΔН_{ф. п}), т. е.

Теперь задача определения ΔН_Т может быть решена, если известен температурный ход теплоемкости каждого из участников реакции. В ряде случаев ход теплоемкости с температурой может быть выражен в виде ряда:

Тогда для Δс_Р аналогично

Δс_Р = Δс_Рº + ΔаТ + ΔbT 2 + ΔcT 3 + …

Подставив это выражение в уравнение для ΔН_Т и проинтегрировав его в пределах от T 0 до Т, получим:

При наличии в системе фазовых превращений ход рассуждений остается тем же, нужно только воспользоваться формулой для ΔН_Т, где учтено изменение энтальпии при фазовых превращениях.

Определение температурного коэффициента напряжения при температуре Т можно провести, воспользовавшись соотношением

из которого следует, что

Подставив вместо Δс_Р степенную зависимость и проведя интегрирование, окончательно получим изменение энтропии системы при интересующей нас температуре:

Разделив теперь ΔS_T на zF, получим температурный коэффициент и с помощью формулы Гиббса — Гельмгольца определим напряжение системы Е_T. Следует помнить, что Е_T относится к температуре Т и активностям участников реакции, равным единице.

Когда в реакции, протекающей в электрохимической системе, имеются газообразные участники, напряжение системы оказывается зависящим от давления. Для определения напряжения как функции давления (Е_Р) следует воспользоваться термодинамическим соотношением

где V — изменение мольного объема при реакции.

Так как ΔG_V = – zFE, то

Интегрирование этого выражения дает:

Если изменение объема подчиняется уравнению состояния идеального газа, то

и

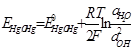
Здесь Е_P — напряжение системы при давлении Р, стандартной температуре и активностях всех конденсированных участников реакции, равных единице.

Если конденсированные участники реакции находятся не в стандартных состояниях, то это обстоятельство должно быть учтено при расчетах, но такие расчеты выходят за рамки книги.

Рассмотрим теперь формулу Гиббса — Гельмгольца применительно к системам без химической реакции.

В системах с электродами из разных модификаций одного и того же металла, например в системе

Sn (белое) | SnSO₄ | Sn (серое)

ΔH – изменение энтальпии при аллотропном переходе серого олова в белое. При температуре, отвечающей равновесию обеих модификаций, ΔG = 0 и, следовательно, Е = 0, откуда

т. е. все изменение энтальпии эквивалентно изменению связанной энергии системы.

Аналогичные рассуждения можно применить и к системам типа

М (жидкий) | Расплавленная соль | М (твердый)

(где М — металл), например

при температуре плавления. Поскольку при плавлении энтальпия изменяется, то, на первый взгляд, можно было ожидать, что при замыкании такой системы потечет ток и произойдут процессы растворения жидкого металла и восстановления ионов металла на твердом электроде. Однако такое заключение ошибочно, ибо при температуре плавления ΔG = 0 и вся теплота, затрачиваемая на плавление, идет на увеличение связанной энергии системы. Следовательно, в этом случае напряжение системы равно нулю и она не может совершить работы.

В остальных типах систем без химической реакции никаких превращений не происходит, а электрическая работа совершается в результате переноса энергии от более высокого уровня к менее высокому уровню. Поскольку в случае идеальных систем внутренняя энергия U не зависит от объема, то ΔH = 0 и

Следовательно, электрическая работа в таких системах совершается только вследствие изменения связанной энергии. Преобразовав это уравнение

откуда после интегрирования имеем

ln E = ln Т + const и E = k’T

В идеальных электрохимических системах данного типа напряжение, таким образом, прямо пропорционально абсолютной температуре.

В реальных же системах (∂U/∂V)_P ≠ 0 и ΔH в формуле Гиббса — Гельмгольца будет равно энтальпии перехода моля вещества от уровня с большей энергией на уровень с меньшей энергией. Например, в системах типа

ΔH — изменение энтальпии при переходе моля растворенного электролита от активности а₂ к активности а₁, т. е. энтальпия разведения в данных пределах (а₂ > a₁).

В указанного типа электрохимической системе не всегда удается достаточно полно элиминировать скачок потенциала на границе двух жидких фаз. Поэтому удобнее воспользоваться двумя одинаковыми электрохимическими системами с химическими реакциями, в одной из которых активность электролита равна а₁, а в другой — a₂, и включить их в измерительную цепь напротив друг другу таким образом, чтобы слева находилась система с большим напряжением:

(–) (Pt) H₂ | HCl, AgCl (тв.) | Ag — Ag | AgCl (тв.), НС1 | H₂ (Pt) (+)

Измеренное напряжение E_p = E₁ – E₂ и, следовательно,

При небольших разностях концентраций разность температурных коэффициентов очень невелика, и таким путем из измерений напряжения можно прямо рассчитать энтальпию разведения от активности а₂ до а₁.

Видео:Вывод формул для энергии Гельмгольца, Гиббса и энтальпии с помощью преобразования ЛежандраСкачать

Уравнение гиббса гельмгольца для равновесной электрохимической цепи

Правильно разомкнутая электрохимическая цепь, на концах которой можно измерить электрическую разность потенциалов, называется гальваническим элементом. Рассмотрим электрохимическую цепь, состоящую их электролита, 2 электродов и одинаковых по природе проводников.

Одним из электродов возьмем водородный электрод (Pt, H₂ / HСl), 2 электрод –серебряный (AgСl / Ag).

Чтобы цепь была правильно разомкнута, надо разомкнуть на Ag.

Ag | Pt, H₂ | HСl | AgСl, Ag

Схема правильно разомкнутой электрохимической цепи.

| — граница раздела фаз.

В этой цепи 3 границы раздела фаз и разность внешних потенциалов ∆Е ═ алгебраической сумме 3 скачков

Таким образом, разность в-потенциалов правильно разомкнутой цепи складывается из скачков гальвани-потенциалов на каждой из границ раздела.

Выражения для этих гальванипотенциалов вытекают из условий равновесия на каждой из фазовых границ.

Условия фазового равновесия:

1 гр. Равенство электрохимических потенциалов двух разных Ме:

II (на 2 границе)

III (на 3 границе)

Складывая между собой уравнения для потенциалов на фазовых границах, получим с учетом выражения для электрохимического потенциала i-того компонента следующее выражение ∆Е

Если число перенесенных электронов в электрохимической цепи больше 1, то число Фарадея умножается на n.

Суммарная химическая реакция, которая лежит в основе работы рассматриваемого гальванического элемента имеет следующий вид:

Ag С l + ½ H ₂ = Ag + H С l

полуреактивное окисление ½ H₂ – е = Н + ; Ag + + е = Ag п/р восстановление

ионное суммарное ½ H₂ + Ag + = Н + + Ag

Для этой реакции можно записать изменение свободной энергии Гиббса ∆G

∆Ν – изменение числа молей в ходе реакции

Сравнивая выражения для ∆G и ∆Е имеем

— ∆ G = F n ∆Е = A ′ _max

A′_max – максимально полезная работа по определению изобарического – изотермического потенциала.

∆Е, равное разности потенциалов на концах правильно разомкнутой электрохимической цепи, называется ЭДС гальванического элемента и может служить критерием при определении направленности окислительно-восстановительных реакций. Процесс будет самопроизвольным при ∆Е > 0.

Для измерения ЭДС гальванических элементов применяют компенсационный метод, при котором разность потенциалов на концах электрохимической цепи компенсируется выверенной по эталону разностью потенциалов от внешнего источника тока. Упрощенная схема компенсационного метода имеет следующий вид:

На реохорде будут включены некоторые сопротивления. В соответствии со схемой Е_х определяется из соотношения Е_х/Е_эт = е_х/е_эт = I R_х/I R_эт; Е_х=Е_эт·е_х/е_эт .

Знак эдс устанавливается по отношению правого электрода к левому. Условленно, что электрохимическая цепь для измерения электродных потенциалов составляется таким образом, что на месте правого электрода всегда исследуемый электрод, на месте левого – электрод сравнения.

Если при этом ∆Е получается больше нуля, то процесс самопроизвольный и на правом положительном электроде (катоде) идет процесс восстановления. Если ∆Е

Так как величена ЭДС гальванического элемента складывается из скачков потенциалов на границах электрод-раствор, то величена ЭДС будет зависеть не только от природы электрода, но и от активности или концентрации электролита или его отдельных компонентов.

В рассматриваемом гальваническом элементе такими компонентами являются Н₂ (газ), Н + , Cl — (ионы в растворе) и Ag, AgCl (твердые вещества). Химические потенциалы твердых веществ не изменяются в растворе и отвечают стандартным значениям, то есть μ 0 _Ag и μ 0 _AgCl. При условии, что водород подается к платиновому электроду под давлением в 1 атмосферу (10 5 – нормальные условия), то потенциал водорода также будет стандартным μ 0 _Н 2 . Для ионов же в растворе имеет место уравнение Нернста для химического потенциала:

Подставим эти выражения в уравнения для ∆Е и ∆G

В этом случае член в скобках отвечает величине ∆G 0 .

Полученное выражение отвечает величине ЭДС рассматриваемого гальванического элемента в произвольных условиях. Распространяя это уравнение на окислительно-восстановительные реакции в электрохимической системе, получим общее уравнение Нернста для ЭДС:

П_i — произведение по i

ν_ί — стехиометрические коэффициенты в уравнении реакции

a_i – активных элементов.

Для исходных веществ ν_ί для конечных ν_ί>0

В соответствии с этим знак перед логарифмом меняется.

Применяя к электрохимическим реакциям уравнение Гиббса- Гельмгольца в виде:

Можно получить тепловой эффект электрохимической реакции с учетом выражения — ∆G = nF∆Е в виде:

∆Н = -n F∆Е + T d∆Е/dT,

где d∆Е/dT – температурный коэффициент ЭДС; может быть либо плюс, либо минус, поэтому эффект электрохимической реакции будет

и ∆Н 0 только для низких температур

и ∆Н >0 для высоких температур.

Величина температурного коэффициента эдс отвечает изменению энтропии реакции:

по определению ∆S = — d∆G / dT

Таким образом, температурная зависимость эдс позволяет рассчитать все основные термодинамические характеристики окислительно-восстановительной реакции, лежащие в основе работы гальванического элемента. Стандартное уравнение изотермы Вант-Гоффа

дает возможность определить константу равновесия, а, следовательно, глубину окислительно-восстановительной реакции по методу эдс

— n F ∆Е` = — RT ln К_р

Электрохимические цепи строго равновесны лишь тогда, когда они не содержат границы двух различных растворов. При наличии такой границы на ней происходят независимые процессы диффузии, и возникает диффузионный потенциал. Электрохимическая цепь, содержащая границу двух растворов, называется цепью с переносом.

Диффузионный потенциал является гальванопотенциалом в разных фазах, поэтому его нельзя точно вычислить.

Если приравнять ∆G, обусловленное переносом ионов через границу двух различных растворов, к электрической работе, то можно получить общую формулу:

а _i – активность отдельного иона, значение которого не известно.

Если в разбавленных растворах активность отдельных ионов заменить их концентрацией, то задавшись распределением концентрации в области между двумя растворами, величина ∆φ_диф можно рассчитать с небольшой погрешностью по формуле Хендерсона:

Видео:Гальванические элементы. 1 часть. 10 класс.Скачать

Классификация электродов и электрохимических цепей

Электрохимические цепи характеризуются по двум признакам:

1) по источнику электрической энергии в цепи;

2) по наличию или отсутствию в цепи границ двух различных растворов (цепь с (без) переноса).

1. Физические цепи – без переноса источника электрической энергии – служит различие в физическом состоянии двух одинаковых по химическому состоянию электродов. Эти электроды погружены в один и тот же раствор и при работе цепи электрод, находящемся в менее устойчивом состоянии, переходит в более устойчивое. Разновидность физической цепей – алютропические цепи, в которых один из электродов сделан из метастабильной модификации данного металла. Другая разновидность – гравитационные цепи.

2. Концентрационные цепи – отличаются только концентрацией компонентов Red и Ox при одинаковых электродах и растворах. Источником электрической Е в них является разность свободной энергии Гиббса за счет разной активности химических компонентов.

∆ E = ∆ E 0 – ν RTln ( a _± )/ nF

3. Химические цепи – источник электрической энергии – свободная энергия химической реакции. Химическими цепями являются все остальные разновидности гальванических элементов, в которых электроды разного состава. Для электрохимических исследовании в зависимости от назначения исследуются различные типы электродов, которые классифицируются по природе Red и Ox форм.

с _i / — концентрация раствора I , c_i // — концентрация раствора II

Типы электродов

Для электрохимических исследований в зависимости от назначения используются различные типы электродов, которые классифицируются по природе веществ окисленной и восстановленной форм, участвующих в электродном процессе.

Электроды I рода

Электродом 1-го рода называют систему, в которой восстановленной формой Red является металл, а окисленной ОХ — соль данного металла, содержащая простые ионы Ме n+ . Пример такого электрода – система Сu/Сu 2+ , где полуреакция восстановления следующая:

Потенциал такого электрода 1-го рода записывается в соответствии с уравнением Нернста:

Как видно из этого выражения, электроды 1-го рода являются обратимыми по катиону, т.е. их потенциал является функцией активности катиона. Однако, есть электрода 1-го рода, обратимые по аниону.

Например, полуреакция восстановления теллура

2 Те + 2е ↔ Те₂ 2-

Еще к электродам I рода относятся амальгамные электроды, например: амальгама ртути на таллии.

Полуреакция восстановления Tℓ (таллия)

В общем случае формула для потенциала может иметь вид:

a _i – активность ионов сорта i

a _M – активность ионов сорта металла

Для чистых металлов активность является величенной постоянной, поэтому член с активностью металла можно объединить со стандартным потенциалом: Е 0/ =Е 0 -RTln( a_M)/nF. Тогда, для потенциала I рода:

Электроды II рода

Электродом II рода называют систему, в которой металл покрыт слоем его труднорастворимой соли или оксидом, а раствор содержит анионы этой соли или группы ОН — .

Полуреакция восстановления для хлор — серебряного электрода имеет вид:

AgCl + e ↔ Ag + + Cl —

Потенциал такого электрода согласно этому уравнению:

Как видно из этого уравнения электроды II рода обратимы по аниону.

Полуреакция восстановления для ртутно-окисного электрода имеет вид:

Каломельный электрод – это соль Нg₂Cl₂ (серого цвета).

Н g ₂ + Cl ₂ — + 2 e ↔ 2 Hg + 2 Cl —

Электроды II рода используются в качестве электродов сравнения, тогда как электрод I рода – в качестве рабочих электродов.

Электроды III рода

Электроды III рода – это электроды, в которых металлы находятся в контакте с двумя труднорастворимыми солями, а в растворе присутствуют ионы соли с большим произведением растворимости.

I. Pb + | PbCl₂, AgCl, Ag

ПР – произведение растворимости

Ag + Cl + 2e + Pb 2+ ↔ 2Ag + PbCl₂

II. Электрод III рода будет отвечать тому электроду, в котором металл является лишь передатчиком электронов между Red– и ОХ– формой. Такие электроды называются редокс – системами, они обратимы. А в качестве дифферентного металла может быть использована платина или устойчивые к агрессивным средам спеченные порошки карбидов или нитридов переходных металлов, обладающих электронной проводимостью. Одной из классических редокс–систем может быть:

Полуреакция восстановления: I₂ + 2e + I — ↔ I 3-

ферри – ферроцианид К

Полуреакция восстановления: Fe 3+ + e ↔ Fe 2+

III. Третий пример – газовый электрод: кислородный, хлорный, водородный электроды. Представляют собой инертную металлическую пластину, к которой подводится электрохимически активный газ. Молекулы газа адсорбируются на поверхности металла, распадаясь на атомы, а затем участвуя в окислительном процессе с раствором содержащем одноименные ионы, например, стандартный водородный электрод сравнения. Он представляет собой платиновую пластину, покрытую слоем платиновой черни для увеличения истинной поверхности. Эта пластина опущена в 1М раствора H₂SO₄, налитый в емкость, внутрь которой пропускают чистый водород под давлением Р = 1 атм.

Полуреакция восстановления: Н + + ē↔1/2Н₂

Потенциал водородного электрода – ЭДС следующей электрохимической цепи:

Если в правой части цепи активность Н + и давление газа будут стремится к 1, то цепь окажется симметричной и ∆E = 0. Именно такой водородный электрод и принят за стандартный электрод сравнения. Условились в электрохимических цепях при измерении электродных потенциалов стандартные электроды сравнения записывают слева, а исследуемые справа, тогда электродный потенциал будет являться электродвижущей силой электрохимической цепи, построенной из стандартного водородного электрода и полуреакции восстановления на границе исследуемого электрода с раствором. Знак электродного потенциала определяется напряжением тока в данной цепи, совпадающим с направлением движения электронов во внешней цепи. Это соответствует положительному направлению обхода контура.

Видео:Лекция 56 Электрохимические цепи и термодинамикаСкачать

Метод ЭДС при определении коэффициента активности, чисел переноса и произведения растворимости

Для более точного определения коэффициента активности методом эдс используемой химической цепи без переноса эдс такой цепи представлено в виде:

∆Е = Е 0 – d rt / nF ln (L · C) – d rt / nF lnb ±

L = √ d d d+ ₊ ∙ d d- _— , с- концентрация соли в растворе М_d+А _d-

Это уравнение соединяет 2 неизвестных Е 0 и b ±, поэтому строят график зависимости [Е 0 + d rt / nF ln (L · C)] = [Е 0 – d rt / nF lnb ±] от √с

При малых концентрациях соли зависимость lnb ± от √с линейна, т.е. согласно предельному закону Дебая-Гюккеля: lg b ± = – ׀ z ₊ z _— ׀ h √I

Экстраполяция линейного участка графика в с=0 отсекает на ординате ∆Е₀ и рассчитывает b ±.

Для определения чисел переноса методом эдс используется разность потенциалов на концах концентрацной цепи с переносом. Если известны коэффициенты активности в исследуемых растворах, то число переноса можно рассчитать:

Например: цепь (I) Cd/ CdSO₄ CdSO₄/Cd d = 2

Концентрации 2-х растворов не должны сильно отличаться друг от друга. Тогда найденные числа переноса t _– и t ₊ = 1- t будут составлять средней концентрации √с₁∙с_2.

Если измерить разность потенциалов в цепи 1 и в цепи 2:

Cu / Cd / CdCl ₂ / AgCl , Ag / Cd / AgCl , Ag / CdCl ₂ / Cd / Cu

Значение стандартных потенциалов позволяет рассчитать по методу ЭДС произведение растворимости трудно растворимой соли или оксида. Произведение растворимости соли МеА:

E 0 – стандартный потенциал электрода II рода с полуреакцией:

↔

Е 0/ – стандартный потенциал I рода с полуреакцией:

↔М

📽️ Видео

Энергия Гиббса. Практическая часть. 10 класс.Скачать

Лекция 96 Уравнение электрокапиллярности Количественный анализ электрокапиллярной кривойСкачать

Свободная энергия Гиббса и самопроизвольные реакции (видео 8) | Энергия| БиологияСкачать

Решение задач на вычисление энергии Гиббса. 1 часть. 10 класс.Скачать

Электрохимический ряд потенциалов. 1 часть. 10 класс.Скачать

Решение задач на вычисление энергии Гиббса. 2 часть. 10 класс.Скачать

Электрохимия. Гальванический элемент Даниэля-ЯкобиСкачать

Энергия Гиббса и Гельмгольца.Фугитивность и активность.Термодинамические потенциалы.Скачать

Электродные потенциалы металлов. Электроды сравненияСкачать

4 3 Электрохимический потенциалСкачать

Лекция №7 Электрохимические процессыСкачать

Физическая химия 2 Электрохимия — Л. 11 — Термодинамика гетерогенных электрохимических систем (ч. 2)Скачать

Электроды и гальванические элементыСкачать

Румянцева М.Н.- Общая и неорганическая химия. Лекции - 2.Второй закон термодинамикиСкачать

Лекция 2Скачать