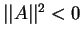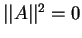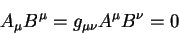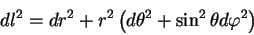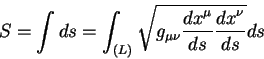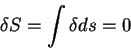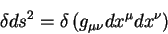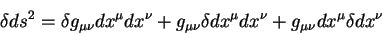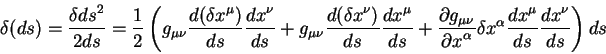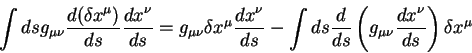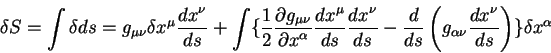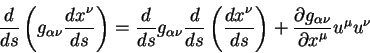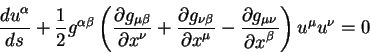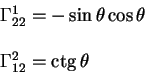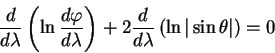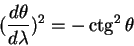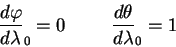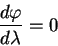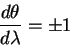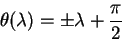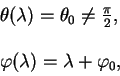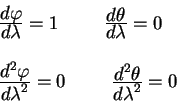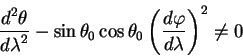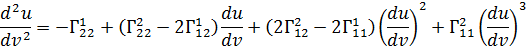- 5. Неэвклидова геометрия
- 5.1 Метрика искривленного пространства — времени
- 5.1.1 Примеры метрики искривленного пространства
- 5.2 Геодезические линии в неэвклидовой геометрии
- 5.2.1 Геодезические линии на поверхности сферы
- Движение по экватору
- Движение по меридиану
- Движение по малому кругу
- Геодезическая линия на поверхности
- Мир трехмерной гиперсферы. Геодезическая трассировка лучей в замкнутой вселенной со сферической геометрией
- Введение. Двухмерный замкнутый мир
- Трехмерный замкнутый мир
- Модель
- Первое знакомство
- Визуальное исследование
- Заключение
- 📸 Видео
Видео:Соотношение между дирекционным углом и румбом в геодезииСкачать

5. Неэвклидова геометрия
В произвольной геометрии рассматриваются произвольные преобразования координат:
как видно из приведенных преобразований, они описывают просто переход от сферических к декартовым координатам.
Дифференциал в нетильдованной системе связан с дифференциалом в системе координат с тильдой уравнениями вида:
В геометрии вводится понятие геометрического объекта. Не перечисляя всех объектов геометрии назовем только скаляры, векторы и тензоры. Строго говоря, все перечисленные величины являются тензорами, так скаляр является тензором нулевого ранга, а вектор тензором первого ранга. Однако исторически принято выделять скаляры и векторы.
Скалярная величина (или скаляр) при преобразованиях системы координат не преобразуется,
Вектором называется величина, которая содержит четыре компоненты, преобразуемые согласно правилу:
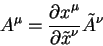 | (5.1) |
для контравариантных компонент и
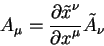 | (5.2) |
для ковариантных компонент.
Как можно заметить, из закона преобразования (5.1) преобразование контравариантных компонент какого — либо вектора подобно преобразованию дифференциалов координат, представляющих разность положений двух точек. Следовательно контравариантные компоненты вектора можно представить как систему из двух точек, с указанием какая из точек является первой, а какая является второй. Примером контравариантных компонент является четырехмерная скорость какого — либо тела.
Примером ковариантных компонет вектора является градиент некоторого поля:
Образом градиента от поля являются наборы двумерных поверхностей определяющих постоянство поля 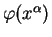
Выпишем также правило по которому преобразуются компоненты тензора второго ранга:
Геометрическая величина 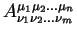
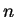
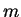
называется тензором ранга 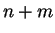
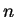
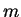
В алгебре тензоров определяется суммирование тензоров одинакового ранга и с одинаково расположенными индексами:
умножение определено для тензоров любого ранга с произвольно расположенными индексами:
В тензорной алгебре определяют также свертку двух тензоров по правилу:
для произвольного расположения индексов важно только, чтобы индекс по которому проводится свертка в первом тензоре был верхним, во втором — нижним (или наоборот, в первом — нижним, а во втором -верхним). Положение и количество остальных индексов переносится в свертку по их месту. Свертки могут быть образованы различными способами, однако каждое суммирование должно выполняться по верхнему и нижнему индексу. Например, сумма
не является тензором, как легко убедиться рассмотрев закон преобразования этой величины.
В современной тензорной алгебре, анализе и физике пользуются правилом суммирования Эйнштейна, который для удобства ввел следущее обозначение:
при этом индекс 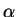
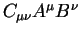
Повсюду в этой книге мы будем использовать это правило, два повторяющихся индекса один верхний, другой — нижний будет означать, что по ним производится суммирование.
Определим также обратные тензоры согласно уравнению:
Здесь 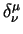
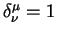
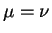
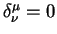
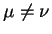
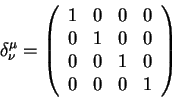 | (5.3) |
Свертка двух тензоров понижает ранг произведения. Так, важный пример показывает, что произведение ковариантных компонент вектора на контравариантные компоненты является инвариантом:
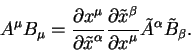 | (5.4) |
Различные авторы [8], [9], [12] вводят также операцию симметрирования, албтернирования, выключения индексов и т.п. Для нас важной остается только последняя операция над тензорами — образование следа, образование поперечной части тензора и образование поперечно — бесследовой части тензора, которые будут применяться во второй части книги. Однако для их определения нам придется использовать метрику, поэтому отложим введения этих понятий после обсуждения метрики.
Видео:Линейные измерения косвенным способом в геодезииСкачать

5.1 Метрика искривленного пространства — времени
Геометрия четырехмерного пространства — времени полностью определяется десятью функциями, которые являются компонентами симметричного тензора второго ранга. Метрика четырехмерного интервала есть:
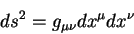 | (5.5) |
Здесь 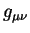
Компоненты метрического тензора являются, вообще говоря, функциями всех четырех координат.
Преобразованием координат всегда можно добиться того, чтобы компоненты метрического тензора были приведены к виду метрики Минковского:
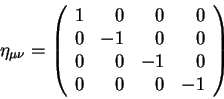 | (5.6) |
В пространстве с заданной метрикой можно определить связь между ковариантными и контравариантными компонентами тензоров, так для вектора связь между этими компонентами задается уравнениями:
Теперь можно определить норму вектора, аналогично тому, как это делается в эвклидовой геометрии. Норомой вектора по определению полагают величину [8], [9], [12]:
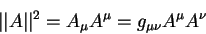 | (5.7) |
В зависимости от того, чему равна норма ветора его называют:
- времениподобным, если
0$» width=»82″ height=»38″ >
- пространственноподобным, если
- изотропным, если
Норма называется также длиной вектора. Как видно из определения изотропного вектора он обладает нулевой длиной.
Рассмотрим свертку двух векторов. Два вектора, которые удовлетворяют условию:
называются ортогональными. Отсюда можно сделать вывод, что изотропный вектор ортогонален самому себе и любому другому изотропному вектору. Следует заметить, что таким свойством обладают только изотропные вектора.
Кроме этого важного свойства приведем также уравнение описывающее угол 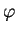
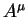
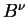
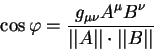 | (5.8) |
Здесь следует заметить, что оба вектора 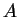
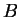
Видео:Ориентирование линий. Дирекционный угол. РумбСкачать

5.1.1 Примеры метрики искривленного пространства
Приведем примеры метрики искривленного пространства. На самом деле в быту мы сталкиваемся с примера геометрии искривленного пространства значительно чаще, чем привыкли думать. Поверхность мяча, поверхность спинки кресла, поверхность кувшина или графина — вот неполный список двумерных искривленных пространств. Примеры идеальных плоскостей, таких как крышка стола или ровный листок бумаги в этом ряду выглядят, скорее исключениями, чем правилом.
Приведем в качестве примера метрику на поверхности сферы. Для этого выпишем вначале метрику эвклидова пространства в сферической системе координат:
Будем считать, что мы вычисляем расстояние только между теми точками, которые лежат на поверхности сферы радиуса 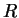
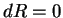
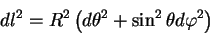 | (5.9) |
теперь метрика описывает поверхность сферы, а геометрия, которую описывает данный метрический тензор является неэвклидовой.
Видео:Попеленский Ф. Ю. - Дифференциальная геометрия и топология. Семинары - Семинар 12Скачать

5.2 Геодезические линии в неэвклидовой геометрии
В эвклидовой геометрии очень важным понятием является прямая между двумя точками, которая к тому же является кратчайшим расстоянием между этими точками. В неэвклидовой геометрии понятие прямой заменяется понятием геодезической линии, которая является экстремальным путем между двумя точками.
Для нахождения уравнения геодезической линиии применим вариационное исчисление.
Длина линии в геометрии общей теории относительности есть интеграл по интервалу между двумя событиями разделенными по времени и пространству:
Линии экстремального пути удовлетворяет условию:
Здесь символ 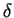
Для вычисления вариации величины 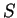
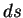
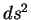
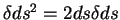
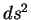
правую часть этого равенства можно представить в виде суммы:
Воспользуемся равенствами 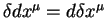
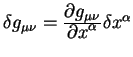
Третий член в круглых скобках уже приведен к виду пригодному для вычисления первой вариации. Для приведения к такому же виду первых двух членов воспользуемся равенством:
Воспользуемся теперь этими равенствами и вычислим первую вариацию полного пути:
В этом уравнении первый член после второго знака равенства представляет из себя вариации в конечных точках пути, по определению эти вариации равны нулю [13], [14]. Член под знаком интеграла в фигурных скобках должен обращаться в нуль на геодезической линии. Это и дает нам уравнение геодезической линии:
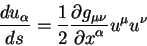 | (5.10) |
Здесь 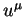
Уравнение, которое мы получили является уравнением второго порядка. В случае эвклидовой геометрии, когда все компоненты метрического тензора являются диагональными и равны единице, правая часть равенства (5.10) равна нулю. Тогда решение этого уравнения есть 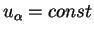
Приведем это уравнение к стандартной форме, принятой в неэвклидовой геометрии. Для этого воспользуемся тождеством:
Подставив его в левую часть уравнения (5.10) получаем уравнение вида:
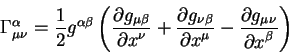 | (5.11) |
называется символом Кристоффеля. Символ Кристоффеля имеет три индекса и не является тензором. В алгебре такие величины носят название символы первого рода.
Стандартный вид уравнения геодезической линии в неэвклидовой геометрии записывается с помощью символа Кристоффеля:
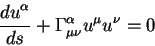 | (5.12) |
Кроме этого, стандартного вида уравнения геодезической линии, можно также записать как меняется дифференциал касательного вектора 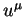
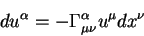 | (5.13) |
Видео:Ориентирование прямых вставокСкачать

5.2.1 Геодезические линии на поверхности сферы
Рассмотрим в качестве примера геодезические линии на сфере — двумерной неэвклидовой поверхности. Метрический тензор на поверхности сферы имеет вид:
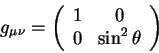 | (5.14) |
Контравариантные компоненты метрического тензора на поверхности сферы есть:
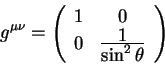 | (5.15) |
Вычисляя символ Кристоффеля получаем, что все компоненты равны нулю за исключением двух:
Уравнения геодезических линий имеют вид:
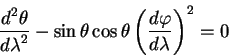 | (5.16) |
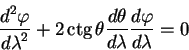 | (5.17) |
Здесь 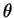
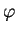
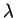
При приведении к первому интегралу уравнение (5.17) получает вид:
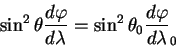 | (5.18) |
Здесь 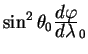
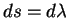
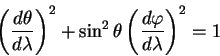 | (5.19) |
Рассмотрим два частных случая геодезических линий.
Движение по экватору
Пусть наша линия начинается на экваторе 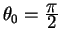
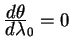
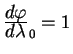
Решение для геодезической линии получается из уравнений (5.18, 5.19). Действительно, правая часть равенства (5.18) есть 1. Подставляем выражение для 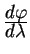
Удовлетворяет этому уравнению только значения 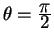
Движение по меридиану
Рассмотрим теперь движение вдоль меридиана и покажем, что меридиан также является геодезической линией. Теперь вектор, касательный к линии имеет компоненты:
Начальную точку также выберем на экваторе 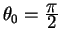
откуда следует, что 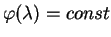
откуда непосредственно следует, что
Не рассматривая общего случая решения системы (5.18, 5.19) упомянем только, что экватор и меридиан на поверхности сферы являются частными случаями большого круга — сечения поверхности сферы плоскостью, которая проходит через центр сферы. Рассматривая трехмерные вращения, можно показать, что только отрезок большого круга на сфере представляет кусок геодезической линии. Полная геодезическая линия представляет из себя большой круг.
Движение по малому кругу
Продемонстрируем отличие произвольной линии от геодезической линии на примере малого круга на сфере. Малый круг на сфере — это сечение сферы плоскостью, которая не проходит через центр сферы.
Выберем малый круг так, чтобы он был сечением с 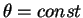
отсюда легко найти первые и вторые производные от координат по афинному параметру:
Подставляя эти значения в уравнения геодезических приходим к противоречию:
Таким образом малый круг на сфере не является геодезической линией.
Видео:Прямая геодезическая задача. Формулировка. ОпределениеСкачать

Геодезическая линия на поверхности
Если прямая линия лежит на поверхности, то она — геодезическая линия этой поверхности. Действительно, кривизна прямой γ тождественно равна нулю. Поэтому в каждой точке P∈γ вектор кривизны k 

Теперь докажем, что геодезическими линиями на плоскости являются прямые и только они.
Первый способ. Как сказано выше, любая прямая, лежащая на поверхности, является геодезической линией. Поскольку через любую точку P плоскости в данном направлении можно провести прямую, и она — геодезическая, то в силу единственности непараметризованной геодезической линии, проходящей через данную точку в данном направлении (теорема 3), других геодезических на плоскости нет.
Второй способ. Пусть Π— плоскость в E 3 . Тогда, в силу замечания можно выбрать прямоугольную систему координат Oxyz в E 3 так, чтобы плоскость Oxy совпадала с плоскостью Π.
В силу того, что кривая γ на поверхности Π является геодезической линией тогда и только тогда, когда ее касательные векторы образуют поле параллельного переноса вдоль γ, и того, что свойство гладкого векторного поля 
Тогда Π задана уравнением z=0 или вектор-функцией 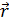
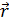
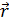
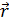
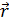


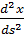

Геодезические на прямом геликоиде
Напомним, что, если прямая линия лежит на поверхности, то она — геодезическая линия этой поверхности. Действительно, кривизна прямой γ тождественно равна нулю. Поэтому в каждой точке P∈γ вектор кривизны k 

Найти геодезические линии на прямом геликоиде 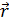
Вычислим матрицу (gij) первой квадратичной формы поверхности и обратную к ней (g ij ):
(gij)= 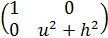

Находим символы Кристоффеля второго рода
( 

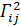

Координатные линии v= const представляют собой прямые и как уточнено выше, являются геодезическими линиями прямого геликоида. Дифференциальное уравнение
запишется в виде:
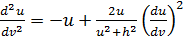
p= 
при этом 

Положимq=p 2 ,тогда
из (2) имеем 
Решаем соответствующее однородное уравнение:


Запишем общее решение однородного уравненияq=c1(u 2 +h 2 ) 2 .В качестве частного решения неоднородного уравнения (3) возьмемq=−(u 2 +h 2 ).Тогдаq=c1(u 2 +h 2 ) 2 −(u 2 +h 2 )— общее решение уравнения (3). Возвращаясь к переменнымu, v, мы получаем:


где c1иc2— произвольные константы, причем 
Ответ:v=c0=constиv=F(u, c1,c2), 
Замечание
Для простоты все отображения, кривые и поверхности предполагаются требуемого класса гладкости.
Напомним, что гладкая кривая ρ=ρ(t), при t∈(α, β), называетсярегулярной,если ρ=0,∀t∈(α, β). Далее все кривые предполагаются регулярными. Все индексы, обозначенные малыми латинскими буквами i, j, k, l, s, mпринимают значения1 и 2, если не оговорено противное. Так же будут использовать тензорные обозначения.
Литература
1. Геодезические линии. Степанов С. Е. 2000г. МАТЕМАТИКА
2. ГЕОДЕЗИЧЕСКИЕ ЛИНИИ НА ПОВЕРХНОСТЯХ. Составители:Жукова Н.И., Багаев А.В. Учебно-методическое пособие. — Н. Новгород :Издательство Нижегородского госуниверситета. — 2008. – 54 с.
3. Картан Э. Внешние дифференциальные системы и их геометрические приложения. М.: Изд-во МГУ, 1962
4. Рашевский П.К. Курс дифференциальной геометрии (3-е изд.). М.-Л.: ГИТТЛ, 1950
Видео:Масштабы в геодезии. Поперечный, линейный, численный. Как читать и как пользоваться.Скачать

Мир трехмерной гиперсферы. Геодезическая трассировка лучей в замкнутой вселенной со сферической геометрией
Хотели посмотреть на мир глазами существа живущего в компактной замкнутой вселенной со сферической геометрией? Посмотреть на мир без ночи? Мир, где на небе виден другой полюс планеты? Мир, где нет разницы между солнечным и лунным затмением? Добро пожаловать под кат!
Введение. Двухмерный замкнутый мир
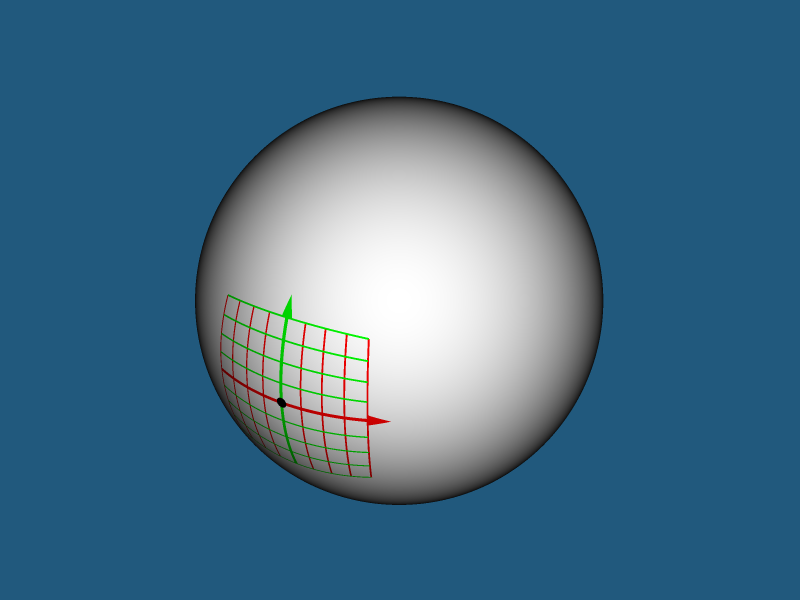
Для того чтобы лучше понять то, что будет происходить дальше вообразим, что вы двухмерное существо и живете в двухмерном мире представляющем собой сферу. Как вы будете воспринимать ваш мир? Начнем с определения положения тел. Вы можете объявить точку, в которой находитесь, «центром вселенной», выбрать два взаимно перпендикулярных единичных вектора и пользоваться полученной декартовой системой координат в окрестностях «центра вселенной».
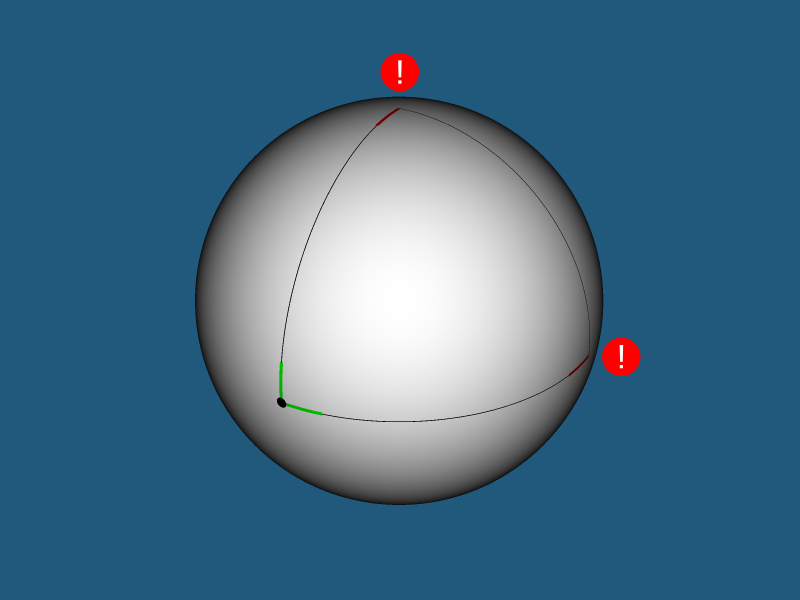
Однако, по мере удаления от «центра вселенной» начнут происходить странные вещи. То, что воспринималось вами как перпендикулярные прямые, при определенном удалении от «центра вселенной» превращается в то, что воспринимается вами как параллельные прямые…
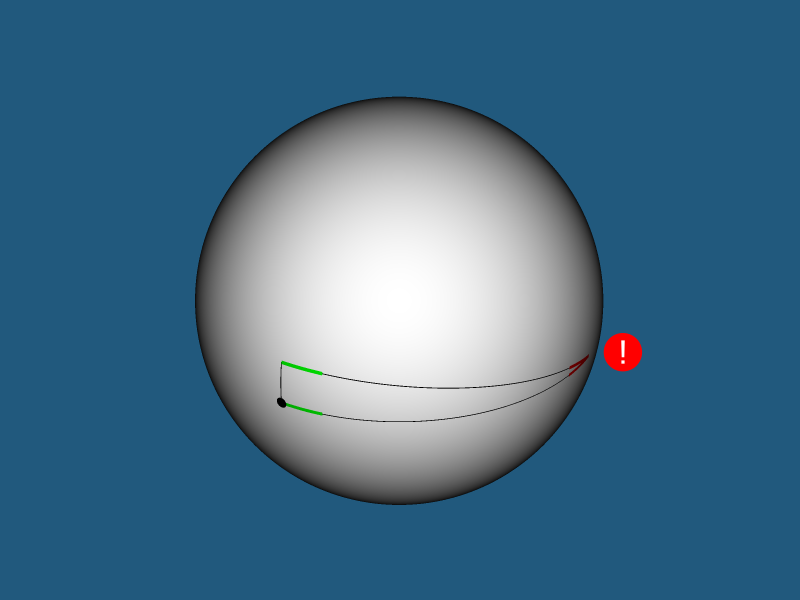
… А параллельные прямые пересекаются.
Причина проста — то, что воспринимается вами как прямая, на самом деле является большой окружностью — геодезической линией сферы. Поэтому декартова система координат непригодна для определения положения тел в вашем мире — при удалении от «центра вселенной» она теряет смысл.
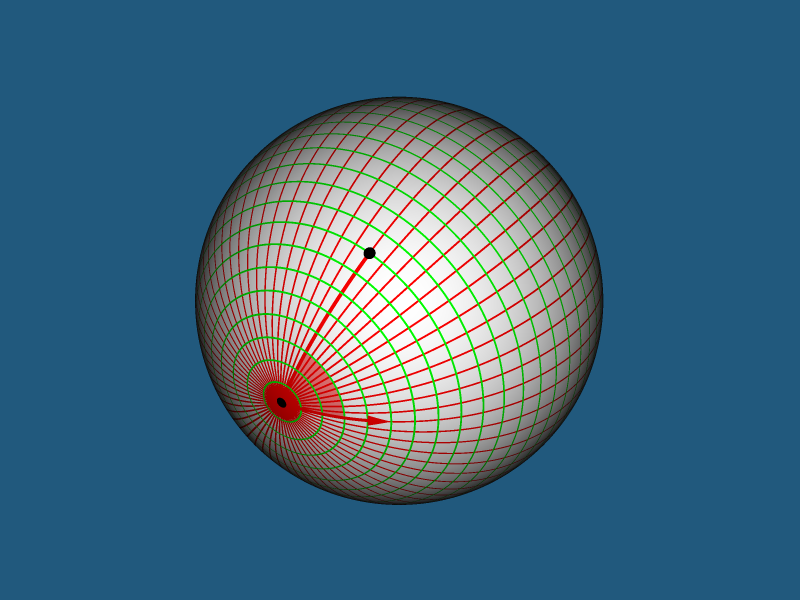
Вам придется выбрать другую, более подходящую для использования в вашем мире, систему координат — полярную. Эта система координат естественна и непротиворечива. Действительно — угол между полярной осью и направлением на тело остается постоянным вне зависимости от расстояния до тела.
Умея определять положение тел, мы можем мысленно исследовать ваш мир и описать некоторые эффекты, проявляющиеся по мере удаления от «центра вселенной» и обусловленные тем, что ваш мир представляет собой сферу.
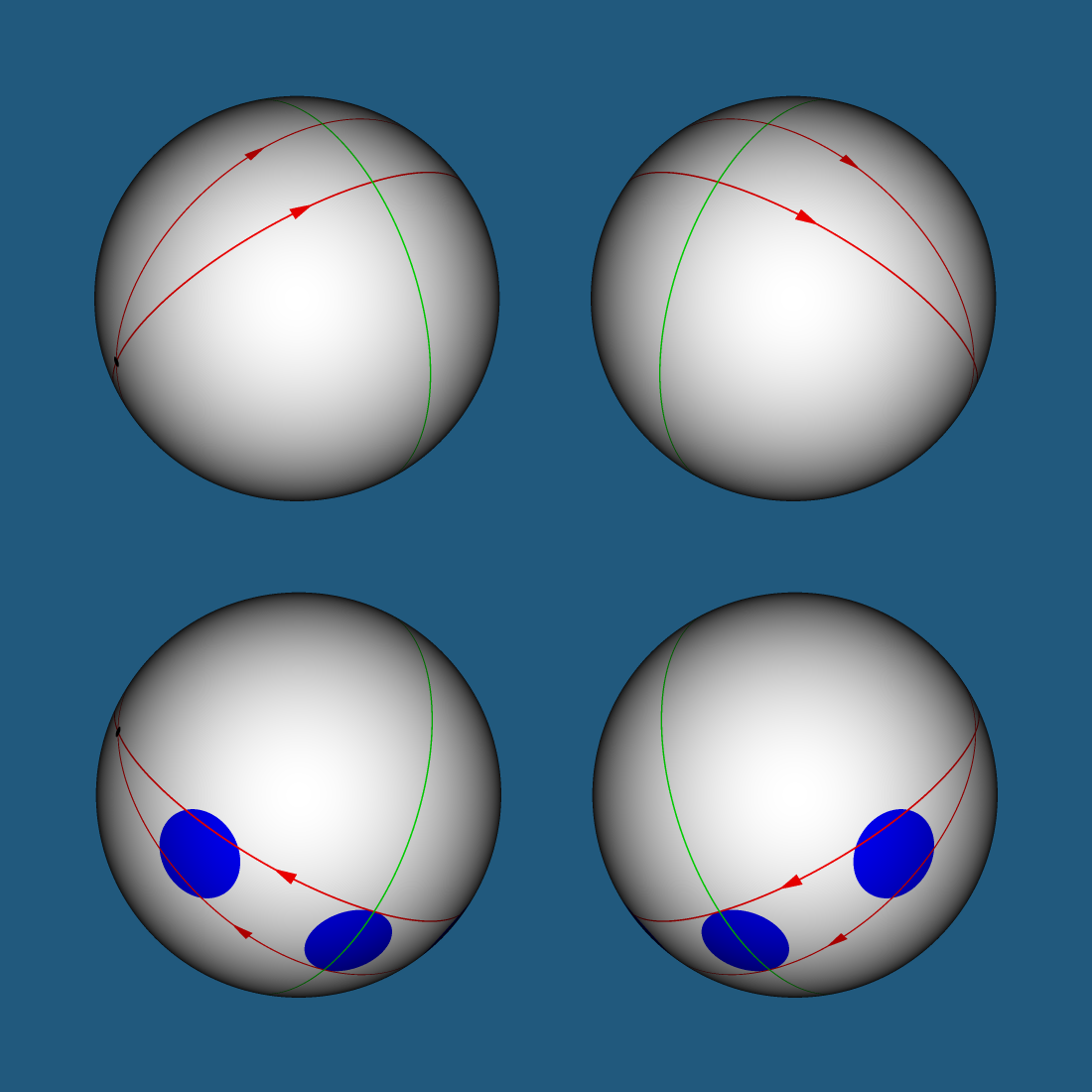
Обратная перспектива. Обычно при удалении тела от «центра вселенной» его угловой размер уменьшается. Однако, на расстоянии больше чем четверть длины геодезической линии от «центра вселенной» при удалении тела его угловой размер будет увеличиваться. Этот эффект связан с тем что расстояние между геодезическими линиями сферы до экватора увеличивается, а после экватора уменьшается. Тело, удаленное на одно и то же расстояние от экватора будет иметь один и тот же угловой размер вне зависимости от того по какую сторону от экватора оно лежит. И этот угловой размер будет больше чем угловой размер тела на экваторе.
Растягивание тела на все небо. Здесь термин все небо используется в значении — все поле зрения двухмерного существа (верхнее и нижнее или переднее и заднее). Если тело находится вблизи точки противоположной «центру вселенной», то куда бы вы ни посмотрели, вы встретитесь взглядом с этим телом. У тела не будет точки, которую невозможно было бы увидеть — каждой точке найдется место на небе. Это предельный случай эффекта обратной перспективы.
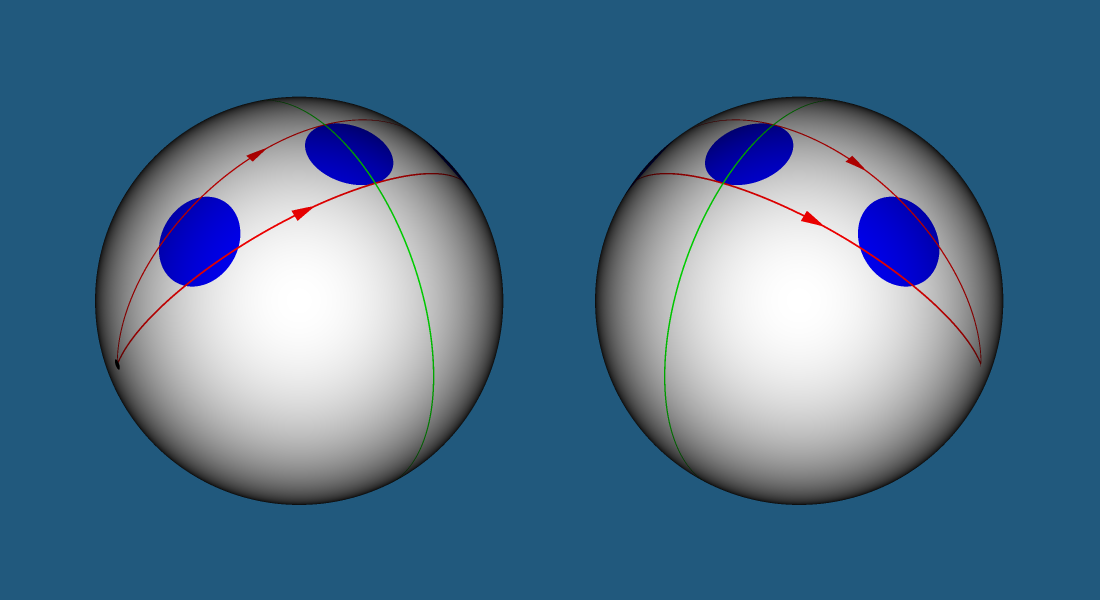
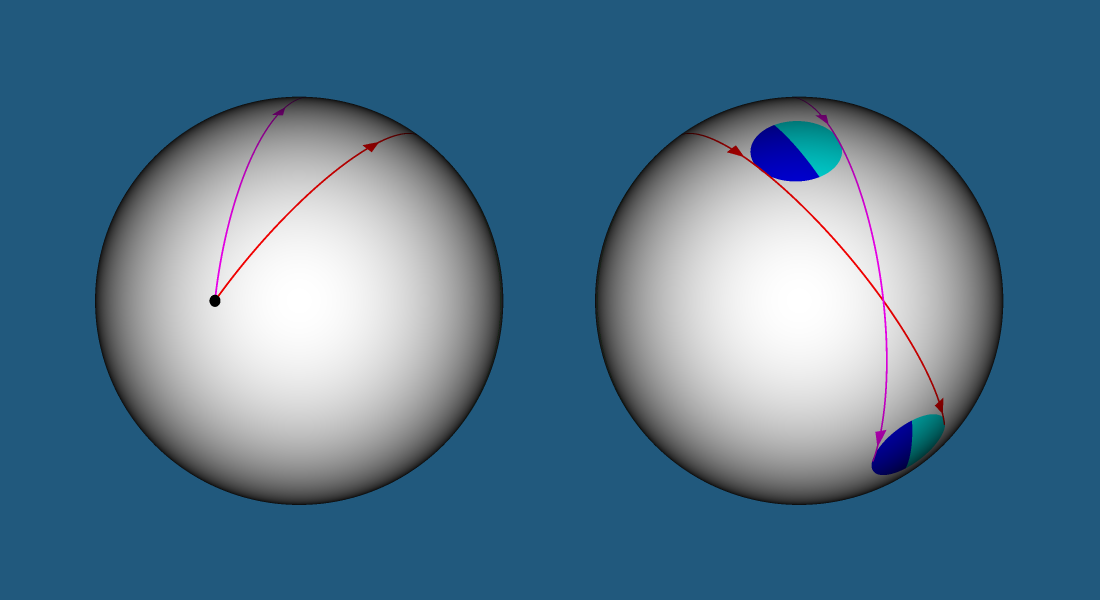
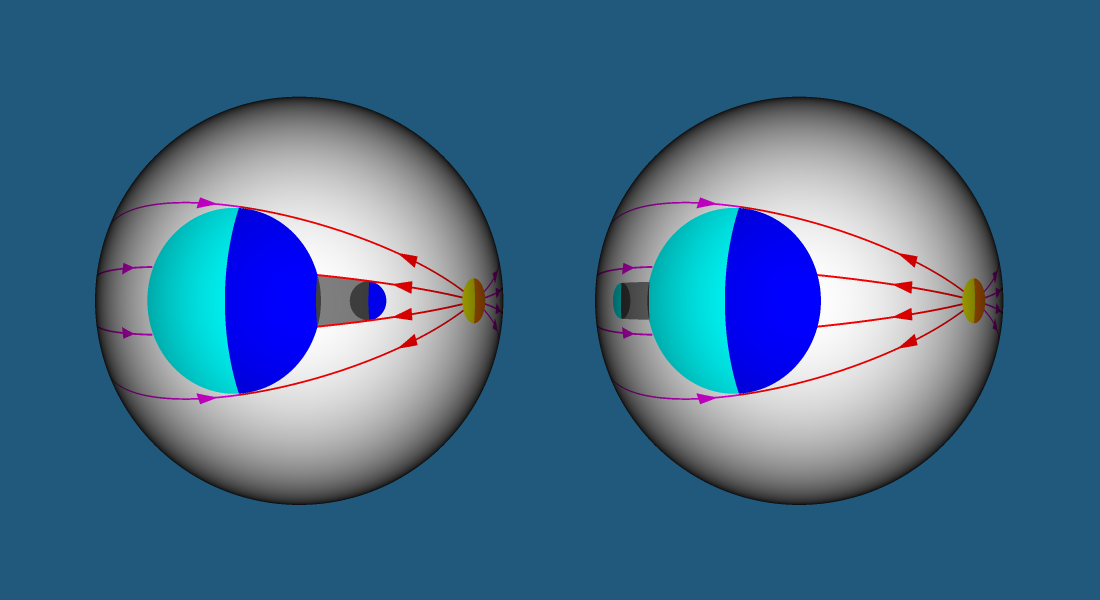
Симметричное преобразование тел. Если тело находится на расстоянии больше чем половина длины геодезической линии от «центра вселенной», то вы будете видеть это тело симметрично преобразованным — левая и правая стороны тела поменяются местами. Обычно левый и правый лучи выпущенные из «центра вселенной» попадают в левую и правую сторону тела. Однако, на расстоянии половины длины геодезической линии от «центра вселенной» лучи пересекаются и после пересечения попадают в противоположные стороны тела.
Вторая прямая и обратная перспективы. Этот эффект так же наблюдается если тело находится на расстоянии больше чем половина длины геодезической линии от «центра вселенной». На расстояниях от половины до трех четвертей длины геодезической линии от «центра вселенной» при удалении тела его угловой размер снова будет уменьшаться (прямая перспектива). На расстояниях от трех четвертей до целой длины геодезической линии от «центра вселенной» при удалении тела его угловой размер снова будет увеличиваться (обратная перспектива). Этот эффект, как и эффект обратной перспективы, связан с изменением расстояния между геодезическими линиями сферы — на обратном пути к «центру вселенной» расстояние между геодезическими линиями сферы до экватора увеличивается, а после экватора уменьшается.
Двойники. У каждого тела в вашем мире будет двойник — если вы видите перед собой тело, то обернувшись вы сможете увидеть его обратную сторону (двойник). Луч, выпущенный по длинному пути, обходит ваш мир и попадает в обратную сторону тела. Следует отметить, что поверхностью двойника будет та часть поверхности, которую вы не видите перед собой, и она будет симметрично преобразованной. Здесь термин поверхность используется в значении — граница двухмерного тела воспринимаемая двухмерным существом — применительно к кругу фактически речь идет о дуге окружности воспринимаемой двухмерным существом как отрезок, однако, для наглядности, мы будем выделять цветом не только дугу, но и лежащую за ней часть круга.
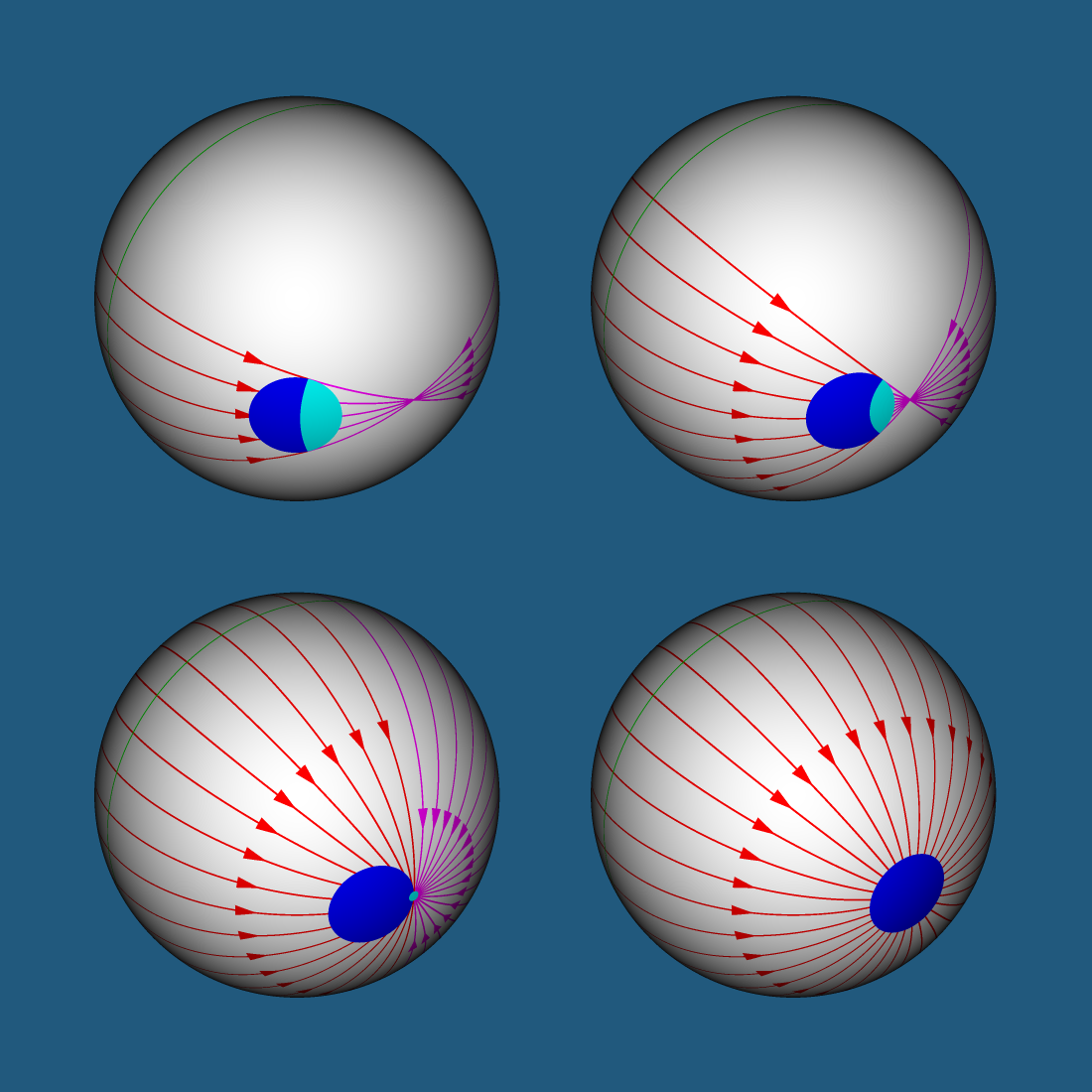
Прохождение тела через точку противоположную «центру вселенной». Поскольку эффект растягивания тела на все небо является весьма необычным мы рассмотрим его подробнее. На рисунках: окрестность точки противоположной «центру вселенной».
- вначале расположенная перед вами поверхность тела увеличивается (окрашена синим цветом), а расположенная позади вас — уменьшается (окрашена голубым цветом); при этом обе поверхности имеют одинаковые угловые размеры — то есть расположенная перед вами поверхность тела стягивается (все большая часть поверхности лежит в пределах каждого градуса), а расположенная позади вас — растягивается (все меньшая часть поверхности лежит в пределах каждого градуса)
- когда тело касается точки противоположной «центру вселенной» угловой размер обоих поверхностей равен 180 градусам — одну половину неба (перед вами) занимает вся поверхность тела, а вторую половину неба (позади вас) занимает точка, лежащая на обратной стороне тела
- пока центр тела совмещается с точкой противоположной «центру вселенной» происходит процесс обратный стягиванию и растягиванию
- когда тело расположено в точке противоположной «центру вселенной» его поверхность в неискаженном виде растянута на все небо
- сползание тела с точки противоположной «центру вселенной» выглядит аналогично
Двойной горизонт. Представим, что вы живете на двухмерной планете. Опустив взгляд вниз, вы видите поверхность вашей стороны планеты, а подняв взгляд вверх, вы видите… поверхность обратной стороны планеты. Причем она будет очень сильно стянута — видна и поверхность обратной стороны планеты и та часть поверхности вашей стороны планеты, которая находится за вашей спиной за горизонтом — вы можете увидеть все это у себя над головой. Небо будет представлено в виде узкой как ниточка полоски зажатой сверху и снизу горизонтами вашей и обратной сторон планеты. Это комбинация эффекта растягивания тела на все небо и эффекта двойника. Вообще, в вашем мире, если вашему взгляду ничего не мешает, то прямо перед собой можно увидеть свой затылок… здоровый такой затылок, во всех подробностях… растянутый на все небо)
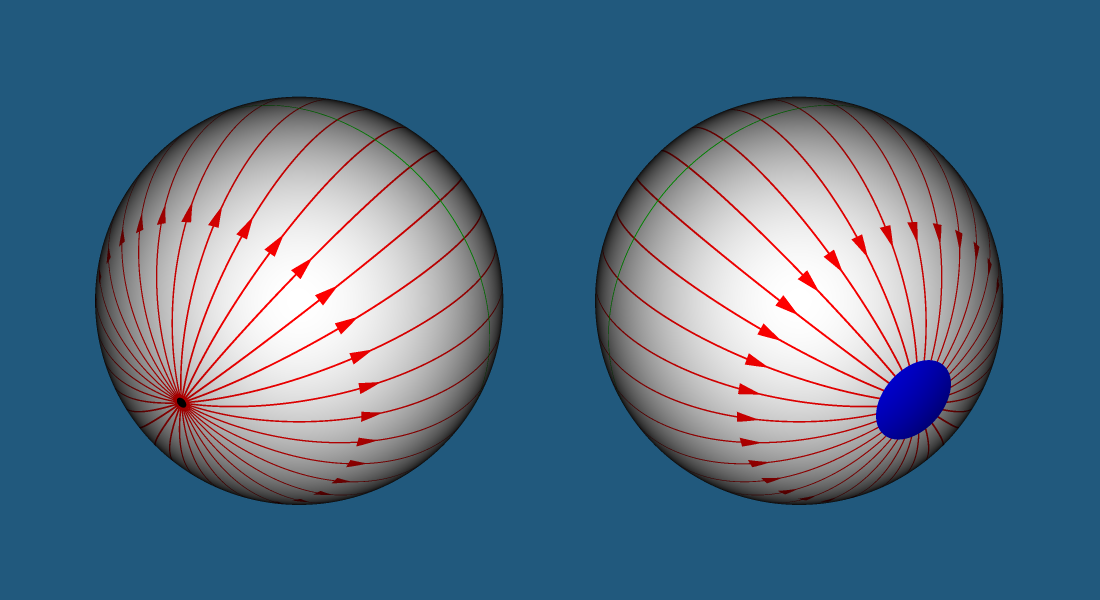
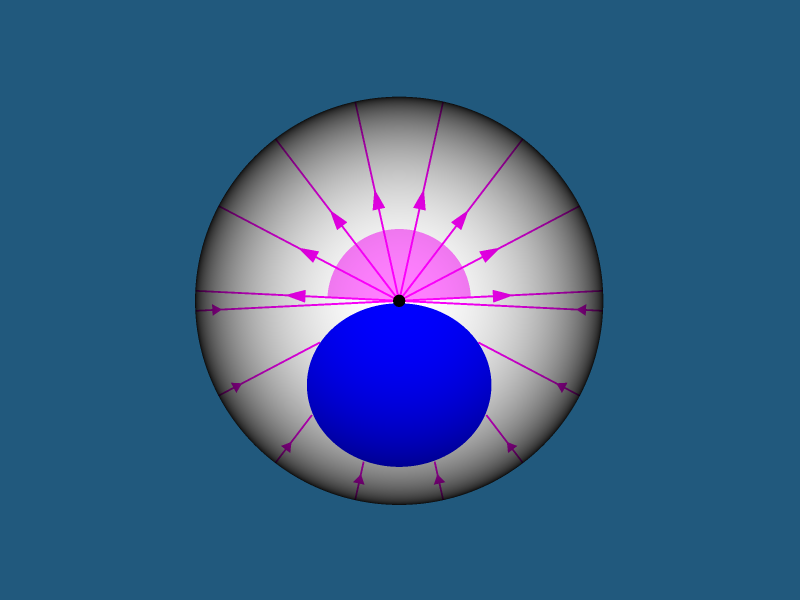
Мир без ночи. Представим, что двухмерная планета на которой вы живете вращается вокруг двухмерной звезды. Свет, испущенный звездой по короткому пути, падает на дневную сторону планеты. В то же время, свет, испущенный звездой по длинному пути, обходит ваш мир и падает на ночную сторону планеты. Ночи больше не существует. Все что осталось — это закаты и рассветы, которые будут происходить одновременно — когда перед вами обращенная к вам сторона звезды начнет заходить за горизонт, позади вас из-за горизонта начнет восходить обратная сторона звезды. Конечно, можно выделить истинные закат и рассвет по длине пути, который прошел свет, но отличить их от двойников будет практически невозможно.
Есть и предельный случай. Если планете не повезло и она находится в точке противоположной звезде, то звезда будет растянута на все небо, но любоваться этим будет проблематично, так как на планету обрушится весь свет испущенный звездой (при отсутствии поглощения и рассеяния света межпланетной средой).
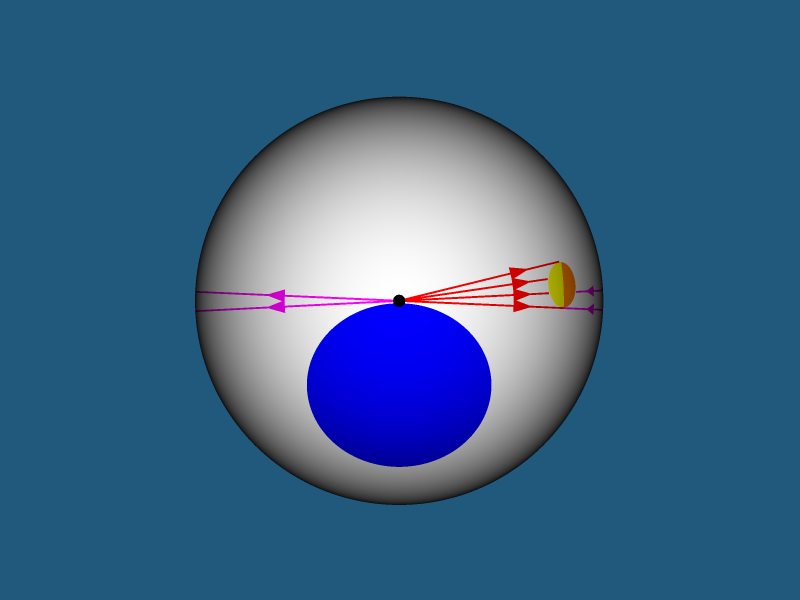
Солнечные и лунные затмения. Представим, что вокруг двухмерной планеты на которой вы живете вращается двухмерный естественный спутник. Когда спутник становится между планетой и звездой его тень падает на планету. С другой стороны в это же время планета становится между светом, испущенным звездой по длинному пути и спутником, то есть тень планеты падает на спутник. Происходит одновременное солнечное и лунное затмения. Конечно, можно выделить истинные солнечное и лунное затмения по длине пути, который прошел свет, но отличить их от двойников будет практически невозможно. Попасть в тень, падающую на планету и ее спутник во время затмений — единственный способ побыть в темноте в вашем мире)
Трехмерный замкнутый мир
Выше мы рассмотрели удивительный мир двухмерного существа. А как насчет нас, трехмерных существ? Какова геометрия Вселенной? К сожалению, наука пока не может дать ответ на этот вопрос. В основном мешают свойства и размер Вселенной. Попробуем помочь науке. Выберем в качестве кандидата наиболее интересную замкнутую вселенную со сферической геометрией и визуально исследуем ее. Будут ли наблюдаться эффекты открытые нами для двухмерного аналога? Может быть, мы узнаем что-то новое? Что-то, чего не ожидали узнать? Или даже увидим то, что видим каждый день, но не обращаем на это внимание? Как вообще будет выглядеть такая вселенная?
Модель
Мы будем исследовать мир, который представляет собой трехмерную гиперсферу (3-сферу) — то есть сферу, лежащую в четырёхмерном пространстве. Выберем один тип объектов для визуализации — сферу (2-сферу принадлежащую 3-сфере).
Декартовы координаты в четырехмерном пространстве — будем обозначать их как — это фактически
.
Гиперсферические координаты в четырехмерном пространстве (используем только углы, так как радиус нашего мира будет константой) — будем обозначать их как — это фактически
.
3-сфера с центром в начале координат — множество точек, радиус-вектор которых имеет длину равную радиусу 3-сферы — это наш мир
2-сфера принадлежащая 3-сфере — множество точек, радиус-вектор которых имеет длину равную радиусу 3-сферы и образует с радиус-вектором центра 2-сферы
угол равный угловому радиусу 2-сферы
— это наши объекты визуализации
— геодезический радиус 2-сферы
Геодезический, угловой и условный радиус — для того что бы лучше понять что это такое рассмотрим двухмерный аналог 2-сферы принадлежащей 3-сфере — окружность принадлежащую сфере.
Красная дуга на рисунке — это геодезический радиус окружности . Красный угол в правой части рисунка — это угловой радиус окружности
. Высота треугольника в правой части рисунка — это условный радиус окружности
.
Переход от гиперсферических координат к декартовым
меняется от
до
меняется от
до
меняется от
до
Пересечение геодезической линии 3-сферы с 2-сферой принадлежащей 3-сфере.
Это соотношение будет использоваться при трассировке лучей. Пусть имеется геодезическая линия выходящая из полюса 3-сферы в направлении определяемом углами
и
— эти углы совпадают с углами определяющими направление в трехмерном пространстве в окрестностях полюса 3-сферы
упростив имеем (1)
подставив (1) в уравнение 2-сферы и упростив имеем (2)
подставив (1) в уравнение 3-сферы и упростив имеем (3)
выразив из (2) имеем
подставив в (3) имеем
Точка на продолжении геодезической линии 3-сферы проходящей через две точки.
Это соотношение будет использоваться при нахождении текстурных координат и внешней нормали в произвольной точке 2-сферы принадлежащей 3-сфере. Пусть
— центр 3-сферы
— центр 2-сферы
— произвольная точка 2-сферы
— искомая точка лежащая на продолжении геодезической линии
на малом угловом расстоянии
от точки
— точка пересечения прямых
и
— точка пересечения прямой проходящей через точку
перпендикулярно прямой
и прямой проходящей через точку
параллельно прямой
— угловой радиус 2-сферы
Если pi$» data-tex=»inline»/>, то следует положить
, а
Найдем
найдем
Мы будем использовать две модели освещения.
Простая модель освещения. В этой модели яркость точки поверхности зависит от косинуса угла между внешней нормалью к поверхности и направлением на наблюдателя. Мы будем использовать ее при построении изображений для пояснительного материала. Фактически — это модель с точечным источником света расположенным там, где находится наблюдатель, в которой яркость точки поверхности не зависит от расстояния до источника света.
Реалистическая модель освещения. В этой модели будет выделенный точечный источник света. Мы будем использовать ее при построении реалистических изображений. Эта модель может учитывать влияние площади волнового фронта на яркость точки поверхности (фактически — влияние расстояния до источника света). В замкнутой вселенной со сферической геометрией площадь волнового фронта прямо пропорциональна квадрату условного радиуса сферы с геодезическим радиусом равным расстоянию от точки поверхности до источника света. При удалении от источника света площадь волнового фронта до экватора увеличивается (лучи света расходятся), а после экватора уменьшается (лучи света сходятся, фокусируются). После прохождения точки противоположной «центру вселенной» происходит обратный процесс: лучи света вначале расходятся, а потом снова сходятся. Кроме того эта модель может учитывать особенности восприятия (закон Вебера — Фехнера).
Для построения изображения будем использовать обратную трассировку лучей. Что бы модель была интерактивной (мы будем осматривать наш мир и перемещаться в нем) изображение должно строиться в режиме реального времени. Поэтому вычисления будем выполнять во фрагментном шейдере (используем WebGL). Интерфейс реализуем на JavaScript.
Первое знакомство
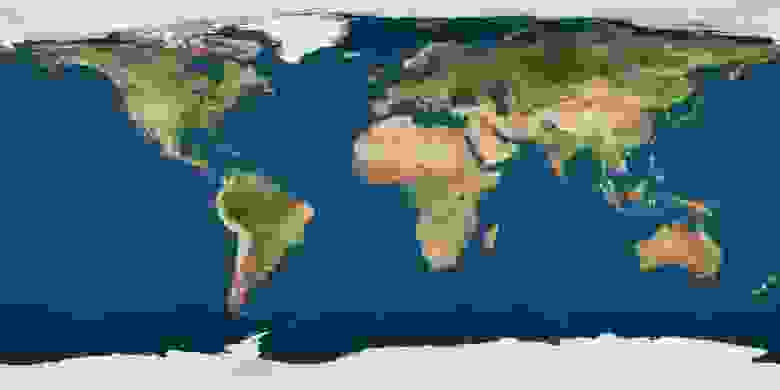
Создадим трехмерный замкнутый мир с длиной геодезической линии равной 100 — так нам будет проще ориентироваться — экватор нашего мира будет расположен от наблюдателя на расстоянии 25 (четверть длины геодезической линии), а противоположный полюс нашего мира — на расстоянии 50 (половина длины геодезической линии). Поместим в наш мир планету и окрасим части ее поверхности в цвета зависящие от того в какой октант они попадают:
| Октант | Знак X | Знак Y | Знак Z | Цвет |
|---|---|---|---|---|
| I | + | + | + | Красный (Red) |
| II | — | + | + | Зеленый (Green) |
| III | — | — | + | Синий (Blue) |
| IV | + | — | + | Оранжевый |
| V | + | + | — | Голубой (Cyan) |
| VI | — | + | — | Пурпурный (Magenta) |
| VII | — | — | — | Желтый (Yellow) |
| VIII | + | — | — | Белый |
В качестве основной текстуры будем использовать текстуру шахматная доска 3×6, то есть каждая параллель и меридиан будут проходить ровно через 12 ячеек. В качестве альтернативной текстуры будем использовать текстуру земной шар. Ниже показаны снимки ознакомительного облета нашей планеты.
Снимок Северного полюса. Ось X направлена вправо, ось Y направлена вверх, ось Z направлена на нас. При наложении альтернативной текстуры можно увидеть:
- справа — Тихий океан
- сверху — Северную Америку
- слева — Атлантический океан
- снизу — Евразию
Снимки перелета от Северного полюса к экватору и от экватора к Южному полюсу.
Снимок Южного полюса. Ось X направлена вправо, ось Y направлена вниз, ось Z направлена от нас. При наложении альтернативной текстуры можно увидеть:
- справа — Тихий океан, Новую Зеландию, Австралию
- сверху — Индийский океан
- слева — Атлантический океан, Африку
- снизу — Южную Америку
Визуальное исследование
Проведем визуальное исследование нашего мира с целью обнаружить аналоги эффектов открытых нами в двухмерном замкнутом мире.
Двойники. Как и в двухмерном аналоге у каждого тела в нашем мире будет двойник — если мы видим перед собой Северный полюс, то обернувшись мы сможем увидеть… Южный полюс. Стягивание поверхности двойника заметно из-за того что мы находимся достаточно близко к планете.
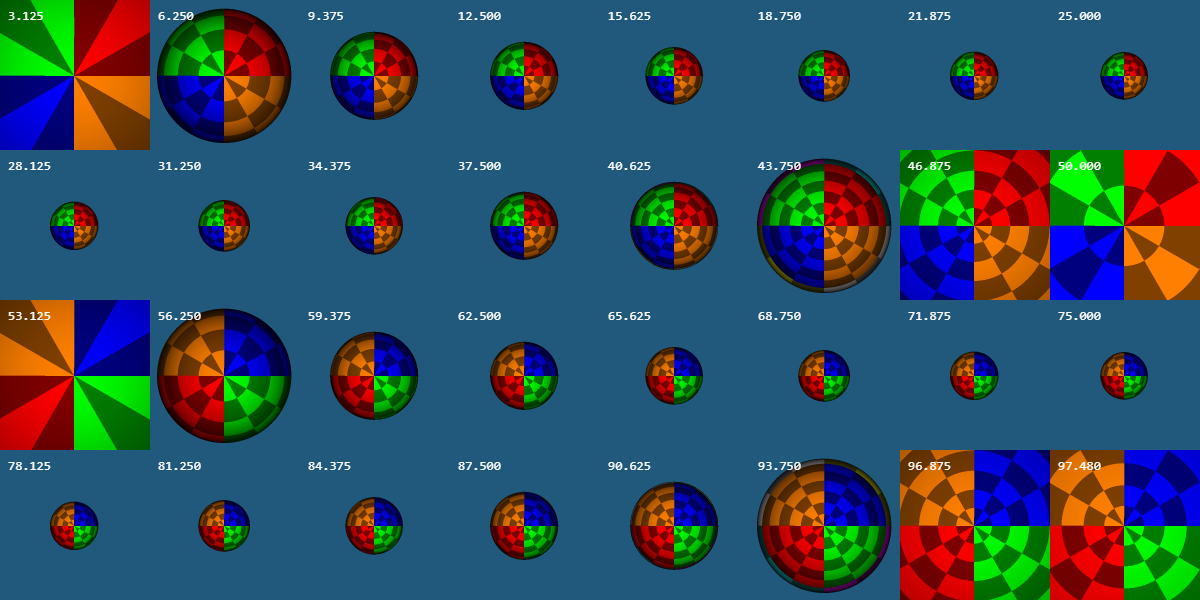
Эксперимент, при котором наблюдатель удаляется от планеты (цифра в левом верхнем углу каждого снимка — это дистанция между наблюдателем и планетой).
- вначале угловой размер планеты уменьшается — это обычная прямая перспектива
- потом, когда планета прошла экватор нашего мира (дистанция более 25), ее угловой размер увеличивается — это знакомый нам эффект обратной перспективы
- при наползании на противоположный полюс нашего мира мы видим стянутую поверхность (дистанция 46,875)
- когда планета находится на противоположном полюсе нашего мира (дистанция 50) ее растягивает на все небо
- при сползании с противоположного полюса нашего мира мы видим растянутую поверхность (дистанция 53,125)
- после того как планета прошла противоположный полюс нашего мира она выглядит симметрично преобразованной — красный октант поменялся с синим и так далее
- затем, угловой размер планеты уменьшается (дистанция от 50 до 75), а потом увеличивается (дистанция от 75 до 100) — это знакомый нам эффект второй прямой и обратной перспективы
Артефакты. При использовании модели было замечено, что во время прохождения планеты через точки лежащие от наблюдателя на расстояниях 25, 50 и 75 возможно появление артефактов — на планете может «вырасти шерсть» или она может вообще «рассыпаться». Видимо моя математика чего-то не учитывает)
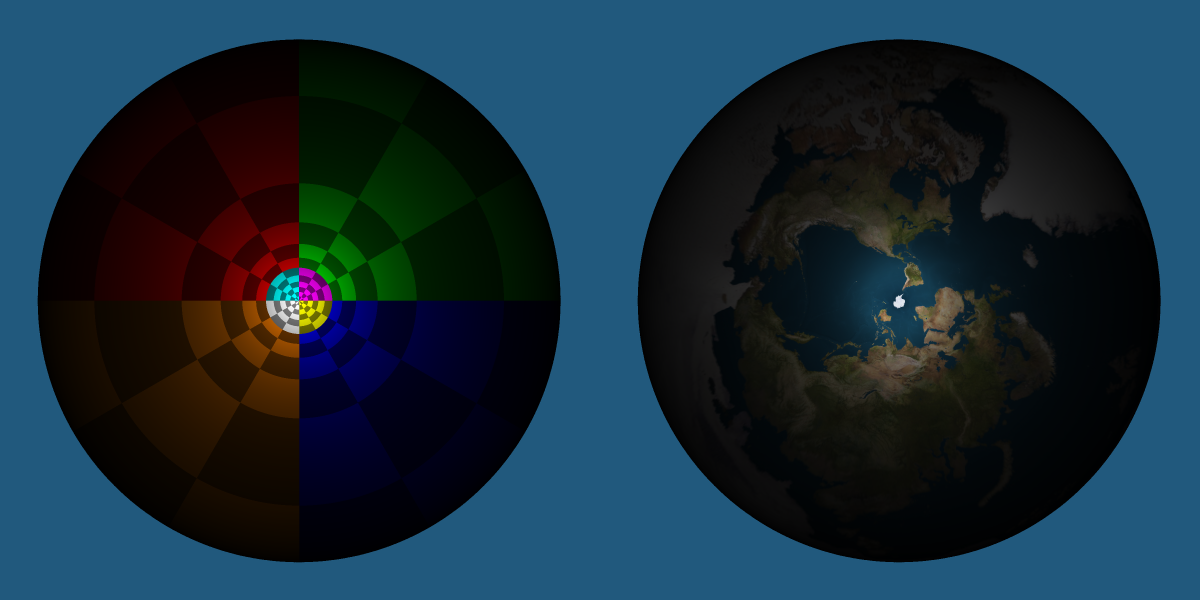
Снимок планеты в окрестностях противоположного полюса нашего мира (использован широкоугольный «объектив»). Поверхность планеты перед нами сильно стянута — видно не только все Северное полушарие, но и часть Южного полушария за экватором. Поверхность планеты позади нас сильно растянута — крупно виден Южный полюс. Обе поверхности тянутся друг к другу пытаясь как бы заключить нас в сферическую оболочку и явить нам картину планеты растянутой на все небо.
Эксперимент, при котором наблюдатель поднимает взгляд (цифра в левом верхнем углу каждого снимка — это угол между направлением вниз и направлением взгляда).
- вначале появляется горизонт нашей стороны планеты
- потом, мы видим над ним второй горизонт, где находим то, что расположено на нашей стороне планеты за нашей спиной за горизонтом
- поднимая взгляд выше, мы видим обратную сторону планеты
Снимок двойного горизонта (использован широкоугольный «объектив»). Полоска неба достаточно велика потому что мы находимся на высоте порядка 50 км.
Снимок неба над головой (использован широкоугольный «объектив»).
Мир без ночи.
Далее для простоты мы будем называть нашу планету Землей, ее естественный спутник — Луной, а звезду вокруг которой они обращаются — Солнцем. Пропорции размеров Солнца, Земли, Луны и их орбит для наглядности не будут соблюдены.
На снимке: граница между дневной и ночной сторонами планеты проходящая через Атлантический океан. Одновременно видны убывающая и растущая Земля. Примерно такую картину видят ребята сидящие на лунных базах в нашем мире)
На анимации: движение границы между дневной и ночной сторонами Земли. Видно перекрытие Солнца диском Земли освещенным лучами Солнца выпущенными по длинному пути.
Солнечные и лунные затмения.
На снимке: Луна выходит из тени Земли. Видны границы между дневной и ночной сторонами Земли и Луны.
На анимации: солнечное и лунное затмения.
- вначале Земля отбрасывает тень на Луну, а Луна отбрасывает тень на Землю
- потом Луна выходит из тени Земли, а тень Луны уходит с поверхности Земли
- затем тень Луны возвращается на поверхность Земли и Луна снова заходит в тень Земли
- граница между дневной и ночной сторонами Луны не видна при перекрытии Луны диском Земли потому что обращенная к нам сторона Луны все еще находится в тени Земли
На анимации: движение границ между дневной и ночной сторонами Земли и Луны совмещенное с солнечными и лунными затмениями. Примерно такую картину видят ребята обслуживающие обсерватории в точке Лагранжа L2 в нашем мире) Конечно, если пренебречь вращением Земли)
На снимке: рассвет на МКС в нашем мире)
Заключение
Для чего все это)? Просто очень хотелось посмотреть на мир глазами существа живущего в компактной замкнутой вселенной со сферической геометрией. Познать этот удивительный мир без символов Кристоффеля и тому подобных вещей оставаясь в рамках общего курса высшей математики. Результат перед вами. Кажется все получилось. Надеюсь, вам было интересно и хорошего дня!
Рабочая модель (открывать на ПК, не для мобильных устройств).
Для тех, кого заинтересовала тематика, есть великолепная статья, в которой рассказывается об удивительных явлениях, которые можно наблюдать в реальной Вселенной: Как нарисовать чёрную дыру. Геодезическая трассировка лучей в искривлённом пространстве-времени.
📸 Видео
Решение обратной геодезической задачиСкачать

Уравнивание ГРО. ГЕОДЕЗИЧЕСКИЕ РАБОТЫСкачать
Смирнов С. В. - Дифференциальная геометрия - Символы КристофеляСкачать

ЧАСТЬ 1. Экзаменационные задачи по инженерной геодезии для 1 курсаСкачать

Дирекционный угол , Истинный азимут, Магнитный азимут,Румб. (геодезия) (4 задание)Скачать

Элементы теории погрешностей в геодезии. Арифметическая середина. Формулы Гаусса и Бесселя.Скачать

Решение обратной геодезической задачиСкачать

Риманова геометрия 4 (семинар). Поверхности вращения. Геодезические линииСкачать

Определение дирекционных углов направленияСкачать

Прямая и обратная геодезические задачиСкачать
Дынников И. А. - Классическая дифференциальная геометрия - Теорема КлероСкачать

Решение прямой геодезической задачиСкачать

Построение горизонталей на топоплане. Аналитический и графический способ. Инженерная геодезия.Скачать

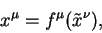
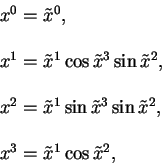
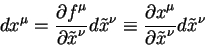
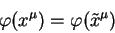
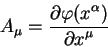
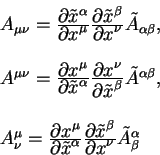
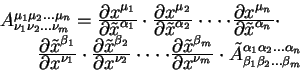
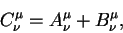
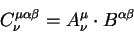
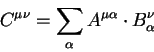
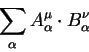
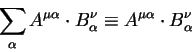
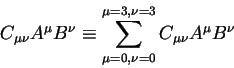
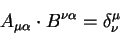
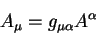
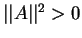 0$» width=»82″ height=»38″ >
0$» width=»82″ height=»38″ >