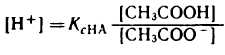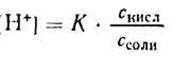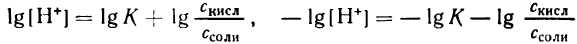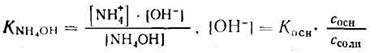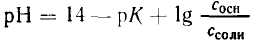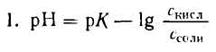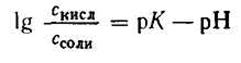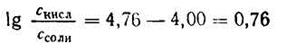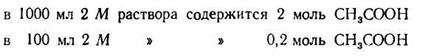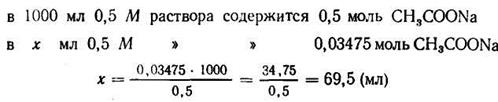Уравнение гендерсона хассельбаха буферных систем

1) Аналитическое выражение для расчета рН буферного раствора, например, ацетатного буфера можно получить из уравнения для константы диссоциации (к реакциям диссоциации применим закон действующих масс).

,

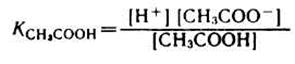
разрешив его относительно концентрации ионов водорода [H + ] можно написать:

Уксусная кислотаприсутствует в растворе в смеси с CH₃COONa в виде неионизированных молекул. Поэтому концентрацию молекул можно принять равной общей молярной концентрации кислоты в растворе, т. е. [СН₃СООН] = С_кисл. Концентрацию анионов уксусной кислоты можно принять равной концентрации соли, т. е. [СН₃СОО — ] = Ссоли, так как CH₃COONa— сильный электролит, диссоциирующий в растворе на 100%. Приняв эти упрощения, получим:

2. Логарифмируя полученное уравнение и заменяя знаки логарифмов на обратные, получаем:

но – Ig [Н + ] есть рН, а – Ig К есть рК — силовой показатель кислоты.

С учетом этого получим:

Это уравнение называют уравнением буферного раствора (или уравнением Гендерсона-Гассельбаха).

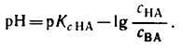
Если при приготовлении буферной системы взять одинаковые концентрации кислоты и соли, то концентрация ионов водорода в таком растворе будет равна константе ионизации кислоты, так как отношение Скис/Ссоли = 1 и [Н + ]=К1, т.е. [Н + ]=К, поэтому рН=рК.

Аналогично для систем NH₄OH + NH₄C1получают выражения:

1. Запишем уравнение константы ионизации NH₄OH и найдем [ОН — ]:

2. Отсюда находим:

Зная, что рН + рОН = 14, получим:

Задача 1. Сколько 0,5 М раствора CH₃COONa нужно прибавить к 100 мл 2М раствора СН₃СООН, чтобы получить буферный раствор с рН=4?

Откуда

Подставляем числовые данные и получаем:

Число Ig 0,76 = 5,754. Следовательно, отношение концентрации кислоты к концентрации соли должно быть равно 5,754 : 1.

2. Находим концентрацию кислоты в буферной системе:

3. Зная концентрацию кислоты, находим концентрацию солив буферной системе; она должна быть равна 0,2:5,754= 0,03475 (моль).

4. Находим количество 0,5 М раствора ацетата натрия, содержащего 0,03475 моль:

Задача 2.Вычислить рН аммиачной буферной системы, содержащей по 0,5 М NH₄ОН и NH₄C1. Как изменится рН при добавлении к 1 л этой смеси 0,1 М НС1 и при добавлении к 1 л этой смеси 0,1 М NaOH и при разбавлении раствора водой в 10 раз, если рК (NH₄ОН) =4,75?

Дата добавления: 2015-08-08 ; просмотров: 10267 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Видео:Буферные системы, ацидоз и алкалоз, ур-ие Гендерсона-Гассельбаха (Атриум и Учим химию)Скачать

Уравнение гендерсона хассельбаха буферных систем

а) Уравнение Гендерсона-Хассельбаха. Как уже обсуждалось ранее, концентрацию ионов Н+ принято выражать не в абсолютных величинах, а в единицах рН. Напомним, что значение рН представляет собой значение -lg ионов Н+.

Аналогичным способом может быть выражена константа диссоциации: рК = -log К.

Следовательно, концентрацию ионов Н+ в уравнении 4 можно выразить в единицах pH через отрицательный логарифм:

Чтобы не производить вычисления с отрицательным логарифмом, можно изменить его знак, поменяв местами числитель и знаменатель дроби согласно правилам логарифмирования. В результате получим:

Для бикарбонатной буферной системы рК равно 6,1, и уравнение выше может быть преобразовано следующим образом:

Последнее уравнение называют уравнением Гендерсона-Хасселъбаха. С его помощью можно рассчитать рН раствора при условии, если известны значения молярной концентрации HCO₃ — и P_CO2. Из этого уравнения становится очевидным, что увеличение содержания HCO₃ — вызывает повышение рН, приводя к алкалозу.

Увеличение P_CO2 снижает рН, смещая кислотно-щелочное равновесие в сторону ацидоза. Уравнение Гендерсона-Хассельбаха, дополнительно определяющее признаки нормального состояния рН и кислотно-щелочного равновесия во внеклеточной жидкости, позволяет понять механизмы физиологической регуляции содержания кислот и оснований во внеклеточной жидкости.

Как будет рассмотрено далее, концентрация бикарбонатов регулируется главным образом почками, тогда как P_CO2 во внеклеточной жидкости зависит от вентиляции легких. Усиление легочной вентиляции способствует выведению CO₂ из плазмы, при снижении показателей вентиляции легких значение P_CO2 возрастает. Гомеостаз кислотно-щелочного состояния поддерживается согласованными действиями обеих систем: выделительной и дыхательной. Повреждение одного или обоих регулирующих механизмов приводит к нарушениям, вследствие которых содержание бикарбонатов или P_CO2 во внеклеточной жидкости изменяется.

Нарушения, смещающие кислотно-щелочное равновесие путем изменения содержания бикарбонатов во внеклеточной жидкости, называют метаболическими, поэтому ацидоз, вызванный таким изменением, носит название метаболического ацидоза, а алкалоз, первичной причиной которого является увеличение концентрации ионов бикарбоната, называют метаболическим алкалозом. При увеличении P_CO2 возникает дыхательный ацидоз, а при снижении — дыхательный алкалоз.

Кривая титрования бикарбонатной буферной системы, отражающая pH внеклеточной жидкости при изменении процентного содержания HCO₃ — и CO₂ (или H₂CO₃) в растворе

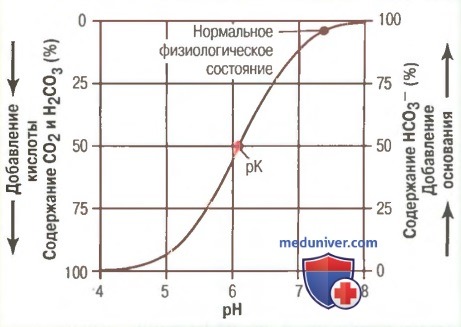
б) Кривая титрования бикарбонатной буферной системы. На рисунке выше показаны сдвиги рН во внеклеточной жидкости в ответ на изменения содержания HCO₃ — и CO₂ во внеклеточной жидкости. Когда концентрации двух этих компонентов равны, правая часть уравнения Гендерсона-Хасселъбаха становится логарифмом 1, который равен нулю, поэтому величина рН раствора такая же, как и рК (6,1) бикарбонатной буферной системы. При добавлении к ней основания часть растворенного CO₂ преобразуется в HCO₃ — , увеличивая значение соотношения HCO₃ — к CO₂ и, соответственно, рН, что становится очевидным из уравнения Гендерсона-Хассельбаха. Добавленная в раствор кислота связывается HCO₃ — , который затем преобразуется в растворенный CO₂, что уменьшает соотношение между HCO₃ — к CO₂ и рН внеклеточной жидкости.

в) Буферная емкость раствора определяется суммарной и относительной концентрацией компонентов буферной системы. Особенность расположения ряда точек, изображенных на кривой титрования рисунке, является вполне объяснимой. Во-первых, при условии, когда доля каждого компонента буферного раствора (HCO₃ — и CO₂) составляет по 50%, рН и рК равны. Во-вторых, буферная система наиболее эффективно действует в центральной части кривой, где рН приближен к рК системы. Это означает, что изменения рН, возникающие в результате добавления к раствору кислот или оснований, в этом диапазоне значений наименьшие. Деятельность буферной системы остается эффективной при отклонениях значений рН в любую сторону в пределах 1, что расширяет границы деятельности буфера от 5,1 до 7,1 единиц. Вне указанных границ буферная емкость быстро снижается. Когда весь CO₂ преобразуется в HCO₃ — или, наоборот, когда весь HCO₃ — преобразуется в CO₂, система полностью теряет емкость.

Абсолютная концентрация компонентов буферной системы также является важным показателем, определяющим буферную емкость. При низкой концентрации компонентов буферной системы добавленные даже в небольшом количестве кислоты и щелочи приводят к значительным изменениям рН.

Редактор: Искандер Милевски. Дата обновления публикации: 18.3.2021

Видео:Буферные растворы и уравнение Гендерсона-ГассельбахаСкачать

Уравнение Хендерсона-Хассельбаха: объяснение, примеры, упражнения

Уравнение Хендерсона-Хассельбаха: объяснение, примеры, упражнения — Наука

Видео:Уравнение Гендерсона-ХассельбахаСкачать

Содержание:

В Уравнение Хендерсона-Хассельбаха представляет собой математическое выражение, позволяющее рассчитать pH буферного раствора или буферного раствора. Он основан на pKa кислоты и соотношении концентраций основания или соли конъюгата и кислоты, присутствующей в буферном растворе.

Уравнение было первоначально разработано Лоуренсом Джозефом Хендерсоном (1878-1942) в 1907 году. Этот химик установил компоненты своего уравнения на основе угольной кислоты в качестве буфера или буфера.

Позже Карл Альберт Хассельбах (1874-1962) ввел в 1917 году использование логарифмов для дополнения уравнения Хендерсона. Датский химик изучал реакции крови с кислородом и влияние на ее pH.

Буферный раствор может минимизировать изменения pH, которым подвергается раствор, путем добавления определенного объема сильной кислоты или сильного основания. Он состоит из слабой кислоты и ее сильного сопряженного основания, которое быстро диссоциирует.

Видео:Буферные растворы и уравнение Хендерсона-Хассельбаха (видео 4) | Буферные растворы | ХимияСкачать

Объяснение

Видео:pH и буферные растворы | Медицинская химия | МедвузаСкачать

Математическое развитие

Слабая кислота в водном растворе диссоциирует по закону действия масс по следующей схеме:

HA — слабая кислота, а A – его сопряженное основание.

Эта реакция обратима и имеет константу равновесия (Ka):

Ka = [H + ] · [TO – ] / [У НЕГО ЕСТЬ]

журнал Ka = журнал [H + ] + журнал [A – ] — журнал [HA]

Если каждый член уравнения умножить на (-1), он выражается в следующей форме:

— журнал Ka = — журнал [H + ] — журнал [A] + журнал [HA]

— log Ka определяется как pKa, а — log [H + ] определяется как pH. После правильной замены математическое выражение сводится к следующему:

pKa = pH — log [A – ] + журнал [HA]

Решив для pH и перегруппировав члены, уравнение выражается следующим образом:

pH = pKa + log [A – ] / [У НЕГО ЕСТЬ]

Это уравнение Хендерсона-Хассельбаха для слабокислотного буфера.

Видео:Буферные растворы. 1 часть. 11 класс.Скачать

Уравнение для слабого основания

Точно так же слабое основание может образовывать буферный раствор, и уравнение Хендерсона-Хассельбаха для него выглядит следующим образом:

pOH = pKb + log [HB] / [B – ]

Однако большинство буферов, даже имеющих физиологическое значение, образуются в результате диссоциации слабой кислоты. Поэтому наиболее часто используемым выражением для уравнения Хендерсона-Хассельбаха является:

pH = pKa + log [A – ] / [У НЕГО ЕСТЬ]

Видео:Уравнение Гендерсона-Хассельбаха в решении задачиСкачать

Как работает буфер?

Видео:КИСЛОТНО-ОСНОВНОЕ СОСТОЯНИЕ №1. Кислоты и основания. Уравнение Гендерсона-Хассельбаха.Скачать

Демпфирующее действие

Уравнение Хендерсона-Хассельбаха показывает, что этот раствор состоит из слабой кислоты и сильного сопряженного основания, выраженного в виде соли. Эта композиция позволяет буферу сохранять стабильный pH даже при добавлении сильных кислот или оснований.

Когда в буфер добавляется сильная кислота, она реагирует с основанием конъюгата с образованием соли и воды. Это нейтрализует кислоту и позволяет минимизировать изменение pH.

Теперь, если к буферу добавлено сильное основание, оно вступает в реакцию со слабой кислотой и образует воду и соль, нейтрализуя действие добавленного основания на pH. Таким образом, изменение pH минимально.

PH буферного раствора зависит от соотношения концентраций основания конъюгата и слабой кислоты, а не от абсолютного значения концентраций этих компонентов. Буферный раствор можно разбавить водой, и pH практически не изменится.

Видео:От чего реально зависит pH крови и что такое уравнение Гендерсона ХассельбахаСкачать

Емкость буфера

Буферная способность также зависит от pKa слабой кислоты, а также от концентраций слабой кислоты и конъюгированного основания. Чем ближе к pKa кислоты pH буфера, тем больше его буферная способность.

Также чем выше концентрация компонентов буферного раствора, тем больше его буферная емкость.

Видео:Буферные системыСкачать

Примеры уравнений Хендерсона

Видео:Буферные растворыСкачать

Амортизатор из ацетата

pH = pKa + log [CH₃COO – ] / [CH₃COOH]

Видео:Буферные растворы. 2 часть. 11 класс.Скачать

Поглотитель угольной кислоты

Однако общий процесс, который приводит к образованию иона бикарбоната в живом организме, выглядит следующим образом:

Быть CO₂ газ, его концентрация в растворе выражается как функция его парциального давления.

pH = pka + log [HCO₃ – ] / α pCO₂

α = 0,03 (ммоль / л) / мм рт.

pCO₂ парциальное давление CO₂

И тогда уравнение будет выглядеть так:

pH = pKa + log [HCO₃ – ] / 0,03 pCO₂

Видео:Буферные растворы. Практическая часть. 11 класс.Скачать

Лактатный буфер

pH = pKa + log [лактат-ион] / [молочная кислота]

Видео:Расчёты pH буферных растворов (видео 5) | Буферные растворы | ХимияСкачать

Фосфатный буфер

pH = pKa + log [двухосновный фосфат] / [одноосновный фосфат]

Видео:Связь pH и pKa для буферных растворов (видео 6) | Буферные растворы | ХимияСкачать

Оксигемоглобин

Видео:Буферная ёмкость (видео 7) | Буферные растворы | ХимияСкачать

Дезоксигемоглобин

pH = pKa + log [Hb – ] / HbH

Видео:лекция 4 Протолитическая теория Буферные системы Решение задачСкачать

Решенные упражнения

Видео:Нормальная физиология | Регуляция кислотно-основного состояния крови. Буферные системы кровиСкачать

Упражнение 1

Фосфатный буфер важен для регулирования pH в организме, поскольку его pKa (6,8) близок к существующему pH в организме (7,4). Каким будет значение отношения [Na₂HPO₄ 2- ] / [Неа₂PO₄ – ] уравнения Хендерсона-Хассельбаха для значения pH = 7,35 и pKa = 6,8?

Реакция диссоциации NaH₂PO₄ – это:

Решая соотношение [конъюгат основание / кислота] для фосфатного буфера, мы имеем:

10 0,535 = 10 log [Na2HPO4] / [NaH2PO4]

Видео:От чего реально зависит pH крови и что такое уравнение Гендерсона ХассельбахаСкачать

Упражнение 2.

Ацетатный буфер имеет концентрацию уксусной кислоты 0,0135 М и концентрацию ацетата натрия 0,0260 М. Рассчитайте pH буфера, зная, что pKa для ацетатного буфера составляет 4,75.

Равновесие диссоциации для уксусной кислоты:

pH = pKa + log [CH₃COO – ] / [CH₃COOH]

Подставляя значения, мы имеем:

[CH₃COO – ] / [CH₃COOH] = 0,0260 М / 0,0135 М

журнал 1.884 = 0.275

Упражнение 3.

Ацетатный буфер содержит 0,1 М уксусную кислоту и 0,1 М ацетат натрия. Рассчитайте pH буфера после добавления 5 мл 0,05 М соляной кислоты к 10 мл предыдущего раствора.

Первый шаг — вычислить конечную концентрацию HCl при смешивании с буфером:

= 5 мл · (0,05 М / 15 мл)

Соляная кислота реагирует с ацетатом натрия с образованием уксусной кислоты. Следовательно, концентрация ацетата натрия уменьшается на 0,017 М, а концентрация уксусной кислоты увеличивается на такую ​​же величину:

pH = pKa + log (0,1 M — 0,017 M) / (0,1 M + 0,017 M)

pH = pKa + log 0,083 / 0,017

Ссылки

1. Уиттен, Дэвис, Пек и Стэнли. (2008). Химия. (8-е изд.). CENGAGE Обучение.
2. Хименес Варгас и Х. Мо Макарулла. (1984). Физиологическая физико-химия. 6-е издание. От редакции Interamericana.
3. Википедия. (2020). Уравнение Хендерсона-Хассельбаха. Получено с: en.wikipedia.org
4. Гуриндер Хайра и Александр Кот. (05 июня 2019 г.). Приближение Хендерсона-Хассельбаха. Химия LibreTexts. Получено с: chem.libretexts.org
5. Хельменстин, Энн Мари, доктор философии (29 января 2020 г.). Определение уравнения Хендерсона Хассельбаха. Получено с: thinkco.com
6. Редакторы Энциклопедии Британника. (6 февраля 2020 г.). Лоуренс Джозеф Хендерсон. Encyclopdia Britannica. Получено с: britannica.com

Что такое белые дыры?

Penicillium roqueforti: характеристика, среда обитания, размножение