Содержание

ЛЕКЦИЯ №6
План лекции:
ЭЛЕКТРОКИНЕТИЧЕСКИЙ ПОТЕНЦИАЛ
ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ
ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ В ДИСПЕРСНЫХ СИСТЕМАХ
Электрокинетический потенциал
🎦 Видео

Видео:СТРОЕНИЕ МИЦЕЛЛЫ - урок 1Скачать

ЛЕКЦИЯ №6

План лекции:

Видео:Гальванические элементы. 1 часть. 10 класс.Скачать

ЭЛЕКТРОКИНЕТИЧЕСКИЙ ПОТЕНЦИАЛ

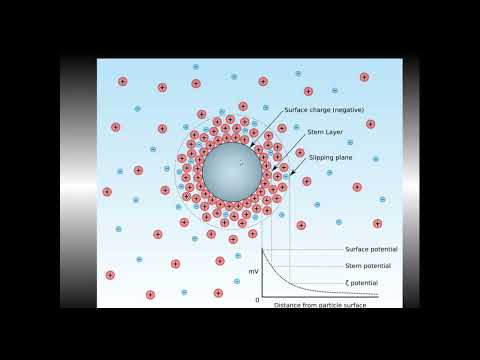
Потенциал j ДЭС снижается по мере удаления от поверхности твердого тела. Причем, в адсорбционном слое наблюдается линейное снижение потенциала. Нарушение линейной зависимости происходит на границе между адсорбционным и диффузным слоями противоионов, в диффузном слое снижение потенциала происходит по экспотенциальному закону и не так резко, как в адсорбционном слое. Потенциал на границе скольжения (рис.6.1, линия ББ) называют электрокинетическим или дзета-потенциалом x .

SHAPE * MERGEFORMAT

На границе скольжения происходит относительное перемещение заряженных частиц и жидкости.

j _д – потенциал на границе между адсорбционным и диффузным слоем.

d — толщина адсорбционного слоя.

Дзета-потенциал — важнейшая характеристика ДЭС, он определяет возможность и скорость относительного перемещения дисперсной фазы и дисперсионной среды, интенсивность электрокинетических явлений, устойчивость золей и разрушение дисперсных систем электролитами.

Значение x -потенциала можно достаточно точно измерить, его знак определяется знаком заряда потенциалообразующего слоя. Если потенциалообразующий слой формируется из анионов, дзета-потенциал будет отрицательным, если образуется из катионов — положительным.

Изменение дзета-потенциала зависит от свойств среды и наличия в ней противоионов. Добавление в дисперсную фазу одновалентных противоионов приводит к сжатию диффузного слоя и снижению дзета-потенциала. Когда все противоионы будут находится в адсорбционном слое происходит полная компенсация потенциалообразующего слоя и дзета-потенциал становится равным нулю. Точку, характеризующую подобное состояние ДЭС, называют изоэлектрической точкой (ИЭТ).

Видео:Электрофорез и электроосмосСкачать

ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ

Появление значительного заряда поверхности является причиной возникновения особых электрокинетических явлений, характерных только для дисперсных систем.

Электрокинетическими называют такие явления, которые возникают при воздействии электрического поля на дисперсные системы и в результате перемещения частиц дисперсной фазы или дисперсионной среды. Несмотря на различие электрокинетических явлений, все они связаны с наличием ДЭС и определяются дзета-потенциалом.

Внешнее электрическое поле вызывает такие электрокинетические явления, как электрофорез и электроосмос.

Электрофорез — это перемещение под действием электрического поля частиц дисперсной фазы относительно дисперсионной среды (рис.6.2).

SHAPE * MERGEFORMAT

1 — потенциалоопределяющий слой ионов.

2 — противоионы в адсорбционном слое.

3 — противоионы в диффузном слое.

При наложении внешнего электрического поля частицы дисперсной фазы начинают двигаться к электроду, знак которого противоположен знаку дзета-потенциала.. Движение частиц происходит по плоскости скольжения ( ББ, рис.6.1).

В процессе электрофореза нарушается сферическая симметрия диффузного слоя противоионов, и он начинает двигаться в сторону, противоположную движению частиц. Противоположно направленный поток частиц диффузного слоя тормозит движение частиц. Этот эффект называют электрофоретическим торможением.

Электрофорез используют для получения новых материалов, нанесения покрытий, очистки веществ от примесей. В медицине электрофорез используют для введения лекарств. На кожу пациента накладывают тампон, смоченный раствором лекарственного препарата, а сверху электроды, к которым приложен безопасный для организма ток.

Электроосмос — перемещение дисперсионной среды под действием внешне

го электрического поля. Движение дисперсионной среды обусловлено притяжением разноименных зарядов.

Когда дзета-потенциал отрицательный, то положительно заряженные противоионы диффузного слоя притягиваются к отрицательному электроду. Положительно заряженные противоионы увлекают за собой жидкость, составляющую дисперсионную среду . В результате этого происходит движение жидкости, причем, перемещение жидкой дисперсионной среды происходит на границе скольжения.

Электроосмос используется, например, для обезвоживания древесины, грунта, продуктов питания.

Все электрокинетические явления связаны с относительным перемещением дисперсной фазы или дисперсионной среды, осуществляемой по границе скольжения. Их интенсивность определяют значением дзета-потенциала. Поэтому данную величину используют для оценки электрокинетических явлений.

ДЭС можно рассматривать в качестве конденсатора. Относительность движения дисперсной фазы и дисперсионной среды определяется силами f ₁ и f ₂ . Сила f ₁ возникает в результате взаимодействия избытка зарядов потенциалообразующего слоя по отношению к адсорбционному слою, она характеризует заряд диффузного слоя и направлена параллельно границе скольжения, противодействуя силе трения.

Е — напряженность или градиент внешнего поля,

Q _B плотность заряда поверхности.

f ₂ — определяет трение жидкости при перемещении.

f ₂ = h ( u / h ) (6.2)

h — коэффициент трения, u — скорость движения жидкости, h – расстояние между поверхностями.

При установившемся движении эти силы равны, то есть:

Е q _В = h ( u / h ) или u = ( q _B h / h ) E (6.3)

(6.3) — определяет скорость взаимного перемещения дисперсной фазы и дисперсионной среды. Удельный заряд q _B – можно связать с дзета-потенциалом.

e _а — абсолютная диэлектрическая проницаемость.

Подставляя равенство 6.4 в 6.3., получим уравнение Гельмгольца-Смолуховского:

Скорость движения в расчете на единицу напряженности электрического поля называют электрофоретической подвижностью u _Е :

С учетом формы частиц дисперсной фазы уравнения 6.5 и 6.6 принимают вид:

u = ( e _а x / h Y )Е (6.7.)

u _Е — электрофоретическая подвижность, м 2 /(сВ),

y — коэффициент , зависящий от формы частиц,

x — дзета-потенциал, В,

Е — напряженость электрического поля, В/м.

y — для шарообразных частиц = 0,66.

y — для цилиндрических, ориентированных вдоль силовых линий электрического поля частиц = 1.

e _а = e e ₀ , где e — относительная диэлектрическая проницаемость,

e ₀ — абсолютная диэлектрическая проницаемость вакуума ( e ₀ = 8,85*10 -12 Кл 2 /(н*м 2 ).

u = ( e e ₀ x / h y )Е = (8,85*10 -12 e x / h y )Е (6.9)

Согласно (6.9.) величины, которые определяют интенсивность электрофореза и электроосмоса, зависят от свойств среды ( h , e ), формы частиц ( y ), напряженности электрического поля (Е) и x ,-потенциала, определяемого структурой ДЭС.

Электрофоретическая подвижность и x -потенциал можно определить экспериментально.

u обычно не превышает 5 810 -8 м 2 /(сВ), а x -потенциал не превышает 100 мВ.

Видео:2.1. Электрокинетические свойства дисперсных системСкачать

ЭЛЕКТРОКИНЕТИЧЕСКИЕ ЯВЛЕНИЯ В ДИСПЕРСНЫХ СИСТЕМАХ

Электрокинетические явления, наблюдаемые в дисперсных системах, представляют собой относительное смещение фаз под влиянием внешнего электрического поля (электроосмос, электрофорез), либо возникновение разности потенциалов при относительном движении фаз, вызываемом гидродинамическими силами (потенциал течения, потенциал седиментации). Электрофорезом называется движение частиц дисперсной фазы относительно дисперсионной среды под действием внешнего электрического поля. Значение электрокинетического потенциала, возникающего при электрофорезе, можно рассчитать по уравнению Гельмгольца-Смолуховского:

(5.1)

где h — вязкость среды;

u — скорость электрофореза;

e — диэлектрическая проницаемость среды;

E – напряженность внешнего электрического поля;

e₀ — электрическая постоянная, равная 8,85 . 10 -12 ф/м.

Значения e и h, подставляемые в уравнение Гельмгольца-Смолуховского, берутся обычно для дисперсионной среды. Для воды при комнатной температуре можно с достаточной точностью принять, что e= 81, а h = 0,001 Па×с.

При электрофорезе на поверхности электрода происходит образование осадка, масса которого зависит от характера электрического поля. При осаждении в неоднородном электрическом поле, заданном системой двух соосных цилиндров, массу осадка m, образующегося на центральном электроде за время t, рассчитывают по формуле

(5.2)

(5.3)

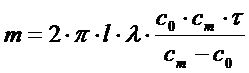
где U – разность потенциалов;

x — электрокинетический потенциал;

l — длина покрытой части электрода;

c₀ – концентрация суспензии;

с_m— концентрация суспензии в предэлектродной зоне;

r₁ и r₂ – радиусы цилиндрических электодов;

e — диэлектрическая проницаемость среды;

e₀ — электрическая постоянная, равная 8,85 . 10 -12 ф/м.

Электроосмос — это движение жидкости (дисперсионной среды) относительно неподвижной дисперсной фазы (капиллярно-пористых материалов, диафрагм) под действием внешнего электрического поля. Из условия стационарного режима электроосмотического движения жидкости в плоском капилляре Смолуховский получил уравнение, связывающее скорость течения жидкости и x-потенциал:

(5.4)

где h — вязкость жидкости;

u – линейная скорость течения;

e — диэлектрическая проницаемость;

E – напряженность внешнего электрического поля;

e₀ — электрическая постоянная, равная 8,85 . 10 -12 ф/м.

Для практического применения более удобна формула, в которую входят величины, измеряемые непосредственно в опыте. Ее можно получить, если выразить линейную скорость u через объемную v , а Е — через силу тока:

(5.5)

(5.6)

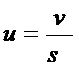
В уравнениях (5.5) и (5.6)

r – удельное сопротивление;

U – внешняя разность потенциалов;

R – электрическое сопротивление;

L – расстояние между электродами;

c — удельная электрическая проводимость.

Подставив (5.5) и (5.6) в (5.4) получим расчетную формулу

(5.7)

Добавочная удельная электрическая проводимость жидкости в капиллярной системе по сравнению с жидкостью вне её называется поверхностной проводимостью c_s. При расчете величины x с учетом поверхностной проводимости в уравнение (5.7) вводится коэффициент активности диафрагмы a:

(5.8)

(5.9)

При течении жидкости через пористую диафрагму под влиянием приложенного давления по длине диафрагмы возникает разность потенциалов, называемая потенциалом течения. Потенциал течения выражается следующим уравнением:

(5.10)

где Р — давление, вызывавшее течение жидкости.

При оседании дисперсных частиц в гравитационном поле двойные электрические слои, окружающие частицу, деформируются за счет трения о слой жидкости. В результате этого диффузные ионы отстают от движущихся частиц и по высоте оседания возникает разность потенциалов, называемая потенциалом седиментации U_сед.

Связь между потенциалом седиментации и электрокинетическим

потенциалом можно установить из уравнения (5.10), заменив давление

Р силой тяжести F_g , вызывающей седиментацию частиц.

(5.11)

где φ — объемная доля дисперсной фазы, равная для сферических частиц радиуса r: 4/3ּπּr 3 ּn,

n — число частиц в единице объема;

ρ и ρ₀ — плотности дисперсной фазы и дисперсионной среды;

g — ускорение свободного падения.

(5.12)

Электрокинетические явления широко используются в науке и технике. Наибольшее их практическое применение связано с нанесением покрытий на различные поверхности электрофоретическим методом. Данный метод позволяет получать равномерные покрытия на деталях сложной конфигурации благодаря его высокой кроющей способности.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

1. Вычислите величину дзета-потенциала на границе кварцевое стекло — водный раствор КСl. Процесс электроосмоса характеризовался следующими данными: сила тока равна 4·10 -4 А; время переноса 10 -8 м 3 раствора КС1 равно 12,4 с; удельная электропроводность среды 1,8·10 -2 Ом -1 м -1 ; вязкость среды равна 1·10 -3 Н·с/м 2 ; диэлектрическая проницаемость среды 81.

РЕШЕНИЕ Связь дзета-потенциала с электроосмотической объемной скоростью v м 3 /с выражается уравнением (5.7):

Вычисляем объемную скорость электроосмоса

м/с,

В.

2. Под каким давлением должен продавливаться раствор КС1 через керамическую мембрану, чтобы потенциал течения был равен 4 . 10 -3 В? Дзета-потенциал без учета поверхностной проводимости равен 3 . 10 -2 В, электропроводность – 1,3 . 10 -2 Ом -1 м -1 , диэлектрическая проницаемость среды 81, вязкость среды 1 . 10 -3 Н . с/м 2 .

РЕШЕНИЕ Из формулы (5.10) без учета поверхностной проводимости

Н/м 2 .

3. Найдите величину дзета-потенциала для суспензии кварца в воде. При электрофорезе частицы перемещаются к аноду; смещение границы составило 5 . 10 -2 м за 30 мин; градиент напряжения внешнего поля равен 10 3 В/м; диэлектрическая проницаемость среды 81; вязкость среда 1 . 10 -3 Н . с/м 2 .

РЕШЕНИЕ Расчет дзета-потенциала по скорости электрофореза ведется по формуле (5.1):

Рассчитываем скорость электрофореза

м/с,

В.

4. Рассчитайте x-потенциал диафрагмы из частиц глины в растворе хлорида натрия с учетом поверхностной проводимости по следующим данным: c = 2,5 . 10 -2 Ом -1. м -1 ; n = 1,2 . 10 -8 м 3 /c; æ_s = 1,65 . 10 -2 Ом -1. м -1 ; h = 1 . 10 -3 Па . с; I = 1,2 . 10 -2 А; e = 81.

РЕШЕНИЕ По формуле (5.9) рассчитывают коэффициент эффективности диафрагмы:

Затем по формуле (5.8) рассчитывают ξ-потенциал с учетом поверхностной проводимости:

В.

5. Рассчитайте массу осадка, полученного на цилиндрическом электроде при электрофорезе водной суспензии карбоната стронция. Длина электрода l = 2 . 10 -2 м; радиус внутреннего электрода r₂ = 1 . 10 -3 м; радиус наружного электрода r₁ = 24 . 10 -3 м; ξ = 35 . 10 -3 В; напряжение на электродах U = 15 B; c₀ = 0,7 . 10 3 кг/м 3 ; η = 1 . 10 -3 Па . с; c_m = 1 . 10 3 кг/м 3 ; ε = 81; τ = 20 c.

РЕШЕНИЕ По уравнениям (5.2) и (5.3) рассчитывают λ и массу электрофоретического осадка (m):

м 2 /c;

кг.

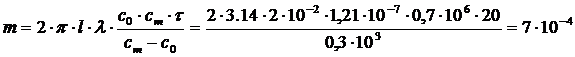
6. Напишите формулу мицеллы золя Sb₂S₃, cтабилизированного SbCl₃ и изобразите графически зависимость x=¦(с) при введении электролитов: NaI_, NaCl, K₄[Fe(CN)₆, KBr.

РЕШЕНИЕ Формула мицеллы золя: <m Sb₂S₃ n Sb 3+ 3(n-x)Cl — > 3xCl — . Перечисленные электролиты являются индифферентными по отношению к данному золю.

Электрокинетический потенциал

Описание: При воздействии на дисперсную систему электрического поля можно наблюдать перемещение дисперсной фазы и дисперсионной среды друг относительно друга. при исследовании электролиза воды. при течении жидкости через пористое тело под действием перепада давлений возникает разность потенциалов. Возникновение разности потенциалов Квинке наблюдал при течении воды и водных растворов через разнообразные пористые материалы глина дерево графит и др.

Дата добавления: 2015-11-10

Размер файла: 1.62 MB

Работу скачали: 22 чел.

Поделитесь работой в социальных сетях

Если эта работа Вам не подошла внизу страницы есть список похожих работ. Так же Вы можете воспользоваться кнопкой поиск

1. Двойной электрический слой

1.1. Механизмы образования двойного электрического слоя

1.2. Строение двойного электрического слоя

1.3. Теория Гельмгольца

1.5. Теория Штерна

2. Электрокинетический потенциал

5. Потенциал течения и седиментации

6. Практическое использование электрокинетических явлений

Список использованных источников

Современная коллоидная химия учение о высокораздробленном состоянии вещества с полным правом может быть названа наукой о коллоидах и поверхностях. Основной коллоидно-химической характеристикой является дисперсность , т.е. рассеянность (раздробленность) вещества. [1]

В более широком смысле определение дисперсности может быть представлено так: дисперсной называют систему, состоящую из дисперсной фазы, которая представляет собой совокупность раздробленных частиц, и непрерывной дисперсионной среды, в которой во взвешенном состоянии находятся эти частицы. [2]

При воздействии на дисперсную систему электрического поля можно наблюдать перемещение дисперсной фазы и дисперсионной среды друг относительно друга. Отсюда следует, что части системы электрически заряжены.

В коллоидных системах, особенно с водной дисперсионной средой, исключительно велика роль электрического заряда на поверхности частиц.

Впервые электрокинетические явления были открыты профессором Московского университета Ф.Ф.Рейсом в 1808г. при исследовании электролиза воды.

Явление перемещения жидкости в пористых телах под действием электрического поля получило название электроосмоса , а явление перемещения частиц электрофореза .

В 1859г. Квинке обнаружил явление, обратное электроосмосу, т.е. при течении жидкости через пористое тело под действием перепада давлений возникает разность потенциалов. Возникновение разности потенциалов Квинке наблюдал при течении воды и водных растворов через разнообразные пористые материалы (глина, дерево, графит и др.). Это явление получило название потенциала течения (или потенциала протекания). [3]

Количественное исследование эффекта, обратного электрофорезу, впервые было выполнено Дорном в 1878г. Он измерял возникающую разность потенциалов при седиментации частиц суспензии кварца в центробежном поле. Явление возникновения разности потенциалов при осаждении дисперсной фазы получило название потенциала седиментации (или потенциала оседания).

Таким образом, по причинно-следственным признакам электрокинетические явления в дисперсных системах делят на две группы:

Электрокинетические явления первого рода относительное перемещение фаз под действием приложенного напряжения. К ним относятся: электрофорез и электроосмос.
Электрокинетические явления второго рода возникновение разности потенциалов вследствие вынужденного относительного движения фаз; различают: потенциал седиментации(эффект Дорна) и потенциал течения(эффект Квинке).

Наибольшее практическое применение получили электрофорез и электроосмос.

1. Двойной электрический слой

При контакте двух конденсированных фаз свойства поверхностного слоя каждой фазы под воздействием второй фазы изменяются. В результате поверхностные слои жидких и твердых тел по структуре, химическим и физическим свойствам значительно отличаются от внутренних объемов этих фаз. Совокупность двух поверхностных слоев при контакте конденсированных фаз называют межфазным слоем . Как правило, межфазные слои в целом электронейтральны. Однако из-за неравномерного распределения заряженных частиц в них могут образовываться двойные слои электрических зарядов противоположного знака, так называемые двойные электрические слои. Согласно современным представлениям двойной электрический слой (ДЭС) можно рассматривать как пространственное разделение зарядов противоположного знака в межфазном слое.[4] Тот факт, что ДЭС состоит из двух слоев противоположных по знаку зарядов, делает его подобным конденсатору.

Рис.1 Двойной электрический слой

на границе металл-жидкость

(диффузное строение слоя)

1.1. Механизмы образования двойного электрического слоя

Двойной электрический слой возникает при контакте двух фаз, из которых хотя бы одна является жидкой. Стремление системы понизить поверхностную энергию приводит к тому, что частицы на поверхности раздела фаз ориентируются особым образом. Вследствие этого контактирующие фазы приобретают заряды противоположного знака, но равной величины, что приводит к образованию двойного электрического слоя. Можно выделить три механизма образования ДЭС:

Переход ионов или электронов из одной фазы в другую (поверхностная ионизация). Примером может служить диссоциация поверхностных функциональных групп, принадлежащих одной из фаз (как правило, твердой). Для определения знака заряда поверхности используется правило Фаянса Панета.
Преимущественная адсорбция в межфазном слое ионов одного знака.
Ориентирование полярных молекул в поверхностном слое. По этому механизму ДЭС образуется в случае, если вещества, составляющие фазы системы, не могут обмениваться зарядами. Для определения знака заряда поверхности используют правило Кёна , гласящее, что из двух соприкасающихся фаз положительно заряжается та, которая имеет большую диэлектрическую проницаемость.[1]

1.2. Строение двойного электрического слоя

Двойной электрический слой состоит из ионов одного знака, относительно прочно связанных с дисперсной твёрдой фазой (потенциалопределяющие ионы), и эквивалентного количества противоположно заряженных ионов, находящихся в жидкой среде вблизи межфазной поверхности (противоионы). Заряд на поверхности твёрдой фазы в первом приближении рассматривается как поверхностный заряд, равномерно распределённый по всей поверхности. Между противоионами и свободными (не входящими в состав двойного электрического слоя) ионами того же знака, находящимися в жидкости, существует динамическое равновесие. Дисперсионная среда представляется всегда как непрерывная фаза, влияние которой на двойной электрический слой определяется лишь её диэлектрической проницаемостью.

При таких предпосылках отличие между теориями строения двойного электрического слоя заключается только лишь в различном толковании структуры слоя противоионов.

1.3. Теория Гельмгольца

Основываясь на экспериментальных данных, полученных Квинке при изучении электрокинетических явлений, Г. Гельмгольц предложил первую модель двойного электрического слоя. Согласно воззрениям Гельмгольца, в дальнейшем развитым М. Смолуховским и Ж. перреном, двойной электрический слой рассматривается как заряженный плоский конденсатор. На поверхности находится слой ионов, называемых потенциалобразующими, а на некотором расстоянии от нее в жидкой фазе

находятся, удерживаемые силой электростатического притяжения, ионы противоположного знака, называемые противоионами. Модель Квинке — Гельмгольца предполагает, что расстояние между плотным слоем противоионов и слоем потенциалопределяющих ионов повсюду одинаково. По условию электронейтральности удельные поверхностные заряды обеих составляющих частей двойного электрического

слоя должны быть равны по абсолютной величине: q + = q — . Скачок потенциала для модели Квинке Гельмгольца рассчитывается по известной формуле для плоского конденсатора q = C ∆ ψ , в которой С емкость плоского конденсатора на единицу площади, причем С=ɛɛ 0 *(1/δ) (ɛɛ 0 диэлектрическая проницаемость среды; δ расстояние между обкладками конденсатора толщина слоя Гельмгольца).

Таким образом, модели Квинке Гельмгольца соответствует скачок потенциала в двойном электрическом слое:

М. Смолуховский и Ж. Перрен предложили формулу (1) для расчета ζ-потенциала по данным электрофореза и электроосмоса.

В модели Гельмгольца не учитывается концентрация электролитов, которая существенно влияет на ζ-потенцциал. [3]

Дальнейший шаг в развитии теории строения двойного электрического слоя был сделан Л. Гуи и независимо от него Д. Чапменом. Используя представления статической термодинамики, эти авторы предложили модель, согласно которой противоионы, не связанные жестко с поверхностью, в отличие от потенциалопределяющих ионов образуют не плоский, а размытый слой, причем концентрация зарядов в нем плавно падает с увеличением расстояния от поверхности. Слой противоионов в теории Гуи Чампена называется диффузным слоем . Его формирование определяется двумя противоположными процессами: притяжением ионов к поверхности за счет электростатического взаимодействия, в связи с чем концентрация их у поверхности должна возрастать, и оттоком ионов из области высоких концентраций, т.е. вблизи поверхности, в объем в результате диффузии.[3] На рис. 3 показано, как изменяется с расстоянием концентрация противоионов и потенциал при таком строении двойного электрического слоя.

Рис.3 Строение ДЭС по Гуи и Чампену

Если воспользоваться распределение Больцмана, то концентрацию анионов в любой точке диффузного слоя можно определить по уравнению:

(2)

где — концентрация анионов в объеме( на «бесконечном» удалении от заряженной поверхности); z _ — заряд анионов; F постоянная Фарадея( F =96485, 33289 Кл*моль); φ разность потенциалов в данной точке и в объеме жидкости( на «бесконечном» удалении от поверхности), В.

Концентрация катионов в этой же точке равна

(3)

где — концентрация катионов в объеме раствора.

Недостаток теории Гуи заключается в том, что она не объясняет явления перезарядки — перемены знака электрокинетического потенциала при введении в систему электролита с многовалентным ионом, заряд которого противоположен по знаку заряда дисперсной фазы. Также теория Гуи не объясняет различного действия разных по природе противоионов одной и той же валентности на двойной электрический слой. Данная теория относительно хорошо выполняется для достаточно разбавленных коллоидных растворов, но оказывается неприемлемой для более концентрированных.

Все эти затруднения в значительной мере преодолены в теории строения двойного электрического слоя, предложенной Штерном.

1.5. Теория Штерна

Современная теория строения двойного электрического слоя основана на представлениях немецкого физика Отто Штерна (1924 г.), который объединил две предыдущие теории. Рассмотрим строение двойного электрического слоя на конкретном примере золе AgI, образованном взаимодействием растворов AgNO 3 и KI. В зависимости от того, какой реагент находится в избытке, на поверхности кристалла AgI могут адсорбироваться ионы Ag + или I . Знак заряда адсорбированных ионов определяет знак заряда поверхности частиц. Пусть адсорбировались ионы Ag + , которые были взяты в избытке (в данном случае заряд поверхности положительный), как изображено на рис. 4. Это потенциалопределяющие

ионы. Они формируют первый слой ДЭС, который находится непосредственно у твердой поверхности.

Плотность поверхностного заряда (ρ s , Кл/м 2 ) определяется количеством потенциалопределяющих ионов на единице площади n i = Г i N А (Г i удельная адсорбция этих ионов, моль/м 2 ; N А число Авогадро) и их зарядом ( z ):

ρ s = zen i = zF Г i , (4)

где e заряд электрона; F = 96485 Кл/моль − число Фарадея.

ПОИ (в данном случае это ионы Ag + ) входят в состав твердой частицы и образуют ее наружный слой. За счет кулоновского взаимодействия они притягивают к себе присутствующие в растворе ионы другого знака анионы NO 3− . Эти ионы называются противоионами (ПИ) . Штерн предположил, что слой противоионов состоит из двух частей. Одна часть примыкает непосредственно к межфазной поверхности и образует адсорбционный слой (слой Гельмгольца) толщиной, равной диаметру гидратированных ионов, его составляющих. Другая часть противоионов находится на более удаленном расстоянии.

Рис.4 Строение ДЭС по Штерну: пространственное распределение ионов (сверху) и изменение потенциала с расстоянием от поверхности твердой фазы вглубь раствора (снизу).

2. Электрокинетический потенциал

Протекание электрокинетических явлений в дисперсных системах возможно при наличии на границе раздела фаз двойного электрического слоя, имеющего диффузное строение. При относительном смещении фаз происходит разрыв двойного электрического слоя по плоскости скольжения(как правило, в диффузной части)(рис. 5).

Рис.5 Разрыв ДЭС по плоскости скольжения

Разрыв двойного слоя может произойти вследствие седиментации или броуновского движения частиц дисперсной фазы. Плоскость скольжения обычно проходит по диффузному слою, и часть его ионов остаётся в дисперсной среде. В результате дисперсионная среда и дисперсная фаза оказываются противоположно заряженными. Потенциал, возникающий на плоскости скольжения при отрыве части диффузного слоя, называется электрокинетическим потенциалом или -потенциалом . Дзета-потенциал, отражая свойства двойного электрического слоя, характеризует природу фаз и межфазного взаимодействия. Плоскость скольжения может находиться на разном расстоянии от межфазной поверхности. Это расстояние зависит от скорости движения фаз, вязкости среды, природы фаз и других факторов. Соответственно от всех этих факторов зависит и значение электрокинетического потенциала. Все факторы, влияющие на толщину диффузного слоя, вызывают изменение -потенциала.

При подобных оценках обычно принимают, что (потенциал диффузного слоя).Понижение температуры, введение в систему индифферентного электролита (специфически не взаимодействующего с поверхностью) и увеличение заряда его ионов ведут к уменьшению электрокинетического потенциала. Этот потенциал будет снижаться и с уменьшением диэлектрической проницаемости среды, например, при добавлении в водный раствор спиртов, эфиров и других органических веществ.

Электрокинетический потенциал, безусловно, сильно зависит от природы поверхности контактирующих фаз. В этом отношении можно выделить два крайних положения: активные и инертные поверхности. Активную поверхность имеют полиэлектролиты полимеры, содержащие ионогенные группы, степень диссоциации которых и определяет заряд поверхности. К веществам, имеющим поверхности с ионогенными группами, можно отнести и многие неорганические оксиды (оксиды кремния, алюминия, железа и др.). На таких поверхностях -потенциал может достигать высоких значений (100мВ и более). Инертные поверхности (графит, масла и др.) лишены ионогенных групп, заряд на них возникает в результате специфической адсорбции ионов.

Специфическая адсорбция может вызвать и уменьшение -потенциала, если адсорбируются противоионы, т.к. они имеют заряд, противоположный заряду поверхности. Такая адсорбция может привести к перезарядке поверхности.

Значительное влияние на -потенциал оказывает рН среды, поскольку ионы Н + и ОН — обладают высокой адсорбционной способностью. Особа велика роль рН среды в тех случаях, когда в контакте с водным раствором находится амфотерное вещество и при изменении кислотности среды возможна перезарядка фаз.

Можно предполагать, что при разбавлении всякой коллоидной системы -потенциал должен возрастать, т.к. толщина двойного электрического слоя увеличивается в результате уменьшения концентрации противоионов в растворе. При разбавлении может наблюдаться десорбция потенциалопределяющего иона с поверхности дисперсной фазы, что должно приводить к падению -потенциала и соответственно -потенциала. Концентрирование коллоидной системы обуславливает, конечно, прямо противоположное действие. В каком направлении в итоге изменяется -потенциал при изменении концентрации коллоидной системы, очевидно, определяется тем, влияние какого из двух факторов утолщения (сжатия) двойного электрического слоя или десорбции (адсорбции) потенциалопределяющих ионов в данном конкретном случае окажется сильнее.

-потенциал дисперсной фазы тем больше, чем больше полярность растворителя, которая характеризуется его диэлектрической проницаемостью дипольным моментом.

Определяемые с помощью электрокинетических явлений знак и значение -потенциала широко используется для характеристики электрических свойств поверхности. При рассмотрении адсорбции, адгезии, агрегативной устойчивости дисперсных систем, структурообразования в материалах и других важных процессах. При этом потенциал диффузной части двойного электрического слоя обычно принимают приблизительно равным -потенциалу. Например, определение изоэлектрической точки (рН иэт ) по нулевому значению -потенциала. [4]

Электроосмос — направленное перемещение жидкости в пористом теле под действием приложенной разности потенциалов. Данное электрокинетическое явление удобно наблюдать с помощью прибора, изображенного на рис.6.

Если поместить в U-образную трубку пористую перегородку (например, мелкий кварцевый песок) и заполнить её водой, то при наложении разности потенциалов в одном колене будет наблюдаться подъем

Рис. 6 Схема опыта по электроосмосу уровня жидкости, в другом его опускание. Движение дисперсной среды в электрическом поле относительно неподвижной дисперсной фазы (в рассмотренном случае относительно поверхности пористых тел) называется электроосмосом.

Схема прибора для изучения электроосмома представлена на рис.7

Рис.7 Схема прибора для изучения электроосмоса; 1-неполяризующие электроды, 2-солевые мостики, 3-градуированная капиллярная трубка.

Постоянный ток от источника через неполяризующиеся электроды 1 и солевые мостики 2 подводится к жидкости по обе стороны пористой диафрагмы. Объем жидкости, прошедшей через мембрану за определенное время, измеряется с помощью градуированной капиллярной трубки 3.

Чем больше потенциал диффузного слоя, тем больше переносчиков зарядов, тем выше скорость перемещения жидкости в пористом теле. Скорость течения жидкости и её направление при постоянной напряжённости электрического поля определяются свойствами мембраны и раствора. Таким образом качественное изучение электроосмоса позволяет однозначно определить знак -потенциала, а количественные измерения установить зависимость между скоростью переноса жидкости и -потенциалом. Изменяя состав и свойства дисперсной среды, можно проследить за изменением структуры двойного электрического слоя по изменению значения электрокинетического потенциала.[1]

Рис.8 иллюстрирует изменение потенциала и скорости движения u в капиллярах пористого тела с изменением расстояния от межфазной поверхности. Направленное перемещение жидкости, вызванное внешним электрическим полем напряженностью Е, уравновешивается действием возникающей силы трения.

Рис. 8 Изменение потенциала φ и скорости течения u с расстоянием от поверхности.

В стационарном состоянии общая сила, действующая на любой сколь угодно малый слой жидкости, равна нулю, и он движется с постоянной скоростью параллельно границе скольжения.

Электрическая сила, действующая на слой жидкости dx (в расчете на единицу площади поверхности), равна:

F эл электрическая сила, Н;

p объёмная плотность заряда, выраженная в соответствии с уравнением Пуассона, м

Е напряженность электрического поля, В/м

Сила трения и её дифференциал, приходящийся на единицу площади (согласно закону Ньютона), составляют:

F тр сила трения, Н

η вязкость дисперсионной среды, Н*с/м

u скорость движения частиц, м/с

При установившемся движении (в стационарном состоянии) dFэл.=dFтр., т.е. приравниваем (5) и (6), получим:

Решение данного уравнения сводится к определению граничных условий интегрирования. При х=l, т.е. на границе скольжения, имеет = и u=0; при х=, т.е. в объёме раствора, =0 и u=0, а и

Окончательно получим следующее выражение для постоянной линейной скорости жидкости относительно мембраны:

Это классическое выражение для скорости движения жидкости при электроосмосе можно получить и на основе представлений двойного электрического слоя как плоского конденсатора, что и было сделано ещё Гельмгольцем. Более строгий вывод соотношения (8) был дан Смолуховским, поэтому уравнение (8) носит название уравнение Гельмгольца-Смолуховского. [4]

Скорость движения дисперсной среды, отнесённая к единице напряжённости электрического поля, называется электроосмотической подвижностью :

Уравнение Гельмгольца Смолуховского чаще записывают относительно -потенциала:

В уравнения (9) и (10) входит электроосмотическая линейная скорость, которую при обработке экспериментальных данных удобнее заменить на объёмную скорость течения жидкости. Используя закон Ома, получим:

где U-внешняя разность потенциалов, В

-удельная электропроводность, См

Окончательное выражение будет иметь вид:

Анализ данного соотношения показывает, что оно справедливо как для единичного цилиндрического капилляра, так и для системы капилляров различной формы, поскольку в это уравнение не входят их геометрические параметры.

Уточним значение электропроводности. Явление электроосмоса наблюдают в узких капиллярах.

При подключении электрического тока наблюдается движение жидкости, и будет разная. Ионы адсорбируются на стенках капилляра. Электропроводность будет больше в капилляре.

— поверхностная проводимость (избыток электропроводности, связанный с наличием на стенках капилляра двойных электрических слоёв).

длина окружности капилляра, м

S сечение капилляра, м

Направленное перемещение частиц дисперсной фазы под действием приложенной разности потенциалов (электрофорез) можно наблюдать в седиментационно устойчивых дисперсных системах. При наложении на такую систему внешней разности потенциалов происходит разрыв двойного электрического слоя по плоскости скольжения, в результате чего частица получает определённый заряд и перемещается к соответствующему электроду.

При электрофорезе можно непосредственно измерять скорость движения частиц. Электрофорез удобно наблюдать с помощью прибора, изображенного на рисунке 9. Прибор представляет собой U-образную трубку, в колено которой вставлены электроды.

Рис. 9 Схема устройства для изучения эдектрофореза; 1-электрод, 2-солевый мостик

Прибор представляет собой U-образную трубку, в колено которой вставлены электроды 1.

Трубку заполняют до уровня исследуемым золем, на поверхность которого наливают контактную жидкость, имеющую одинаковую с золем электропроводность, а на электроды подают напряжение. Через определённые промежутки времени отмечают уровень золя в обоих коленах трубки. Естественно, что скорость перемещения частиц дисперсной фазы определяется значением -потенциала на частицах твёрдой фазы.

Полученное ранее дифференциальное уравнение (7) справедливо для электрофореза, т.к. оно было выведено из баланса движущих сил процесса. Отношение скорости движения дисперсной фазы к напряжённости электрического поля при электрофорезе называют электрофоретической подвижностью:

При выводе соотношений (14) и (15) принимаются следующие ограничения:

частицы движутся в однородном электрическом поле;
частицы могут иметь любую форму и они не проводят электрический ток;
толщина двойного электрического слоя должна быть значительно меньше размера частиц.

Экспериментально определённые значения подвижности оказываются меньше расчетных. Несовпадение экспериментальных и теоретических значений электрофоретической подвижности определяется двумя эффектами: релаксационным эффектом и электрофоретическим торможением.[5]

Релаксационный эффект проявляется в нарушении симметрии диффузного слоя вокруг частицы при относительном движении фаз в противоположные стороны. Возникает внутреннее электрическое поле (диполь), направленное против внешнего поля.

Для восстановления равновесного состояния системы требуется некоторое время время релаксации. Оно достаточно велико, и система не успевает прийти в равновесие, в связи с чем эффективная напряжённость электрического поля Е уменьшается, а следовательно, определяемое экспериментально значение и расчетное значение -потенциала получаются заниженными.

Электрофоретическое торможение обусловлено сопротивлением движению частицы, обратной потоком противоионов, который увлекает за собой жидкость. Вследствие этого электрофоретическая скорость уменьшается. Гюккель, основываясь на теории сильных электролитов, установил, что в уравнение (14) необходимо ввести множитель 2/3 как поправку на электрофоретическое торможение. В дальнейшем было показано, что электрофоретическое торможение является функцией размера частицы и толщины диффузного слоя. Поправка Гюккеля необходима, если толщина диффузного слоя значительно превышает размер частицы; при условии соизмеримости этих параметров её значение может находиться в пределах от 2/3 до 1. [5]

5. Потенциал течения и седиментации

Явление, обратное электроосмосу потенциал течения состоит в том, что при течении дисперсионной среды под действием перепада давления через пористую мембрану на её концах появляется разность потенциалов.

Рис.10 Схема прибора для изучения потенциала течения; 1-электрод, 2-солевые мостики

При изучении потенциала протекания жидкость продавливают через мембрану под давлением ∆р. (Рис.10) Давление создается сжатым баллоном воздуха или насосом. Возникающая разность потенциалов измеряется потенциометром.

Разность потенциалов, в свою очередь вызывает встречный объёмный поток ионов противоположного знака по всему капилляру. После установления равновесного состояния потоки ионов станут равными, а разность потенциалов примет постоянное значение, равное потенциалу течения U. Потенциал течения пропорционален перепаду давления р.

Уравнение Гельмгольца-Смолуховского для расчета -потенциала через потенциал течения имеет вид:

При потенциале седиментации (эффект Донра) как явление, обратном электрофорезу, частицы твёрдой фазы, несущие заряд, осаждаются под действием силы тяжести либо силы центробежного поля. В процессе осаждения ионы диффузного слоя вследствие молекулярного трения отстают

от движущейся частицы, т.е. возникает поток заряженных частиц. Если в сосуде с осаждающимися в жидкости частицами твёрдой фазы установить электроды на разной высоте, то между ними можно измерить разность потенциалов потенциал седиментации.(Рис.11) Этот потенциал пропорционален -потенциалу, частичной концентрации v, а также зависит от параметров системы, определяющих скорость оседания частиц, и электропроводности среды .

Рис.10 Схема прибора для изучения потенциала седиментации; 1-электрод, 2-солевые мостики

Выражение Гельмгольца-Смолуховского для потенциала седиментации:

Частичная концентрация дисперсной системы определяется по уравнению:

где С массовая концентрация дисперсной фазы.

6. Практическое использование электрокинетических явлений

Электрокинетические явления имеют большое практическое значение. Используя их, можно определить весьма важную характеристику дисперсных систем —потенциал, а с помощью электрофореза можно разделять на фракции и характеризировать такие сложные смеси, как природные белки и другие высокомолекулярные электролиты.

Электрокинетические явления широко используются в технике, а также в научных исследованиях нанесение покрытий на различные поверхности электрофоретическим методом. Данный метод, обеспечивающий высокую кроющую способность позволяет получить равномерное покрытие на деталях сложной конфигурации. При электрофоретическом методе нанесения покрытий как правило одним из электродом служит деталь, на которой формируется покрытие, другим ёмкость с суспензией, дисперсная фаза которой наносится на поверхность детали. В зависимости от того, каким электродом (анодом или катодом) является покрываемая деталь, различают анодофорез и катодофорез.

Электрофоретический метод широко применяется также для покрытия катодов радиоламп, полупроводниковых деталей, нагревателей и т.д. Электрофорез используется в медицине, в биологии при выявлении биохимической и физиологической роли различных высокомолекулярных соединений. Этот метод используется также для фракционирования полимеров и минеральных дисперсий.[6]

Явление электроосмоса лежит в основе способа удаления влаги при осушке объектов (стен зданий, сыпучих материалов и т.д.) и способа пропитки материалов различными веществами. Всё большее значение приобретает электроосмотическая фильтрация, сочетающая в себе два процесса: фильтрацию под действием приложенного давления и электроосмотический перенос жидкости в электрическом поле. Применение электроосмоса ограничено большим потреблением электроэнергии.

Явление потенциала течения и седиментации наблюдается в производствах, в которых осуществляется транспортировка жидкостей (перекачка технологических растворов, жидкого топлива), осаждение суспензий и эмульсий при разделении фаз. На концах трубопроводов и аппаратов могут возникать высокие разности потенциалов, которые являются причиной искровых разрядов, вызывающих пожары и взрывы.

Список использованных источников

1. Фридрихсберг Д.А. Курс коллоидной химии. Учеб. для вузов. 2-е изд., перераб.и доп. Л.: Химия, 1984. 368 с., ил.

2. Савицкая, Т. А. Коллоидная химия: строение двойного электрического слоя, получение и устойчивость дисперсных систем. Пособие для студентов химического факультета / Т. А. Савицкая, Д. А. Котиков, Т. А. Шичкова

Минск: БГУ, 2011. 82 с.

3. Захарченко В.Н. Коллоидная химия. Учеб. пособие. 2-е изд., перераб. и доп. М.: Изд-во Высш. шк., 1989. 238 с.

5. Ребиндер П.А. Общий курс коллоидной химии. М.: Изд-во Высш.шк., 1960г.; — 246 с.