Цикл «Занимательная математика» посвящен деткам увлекающимся математикой и родителям, которые уделяют время развитию своих детей, «подкидывая» им интересные и занимательные задачки, головоломки.
Первая статья из этого цикла посвящена правилу Гаусса.
Видео:Метод Гаусса | Школьникам 3-7 классов прежде всегоСкачать

Немного истории
Известный немецкий математик Карл Фридрих Гаусс (1777-1855) с раннего детства отличался от своих сверстников. Несмотря на то, что он был из небогатой семьи, он достаточно рано научился читать, писать, считать. В его биографии есть даже упоминание того, что в возрасте 4-5 лет он смог скорректировать ошибку в неверных подсчетах отца, просто наблюдая за ним.
Одно из первых его открытий было сделано в возрасте 6 лет на уроке математики. Учителю было необходимо увлечь детей на продолжительное время и он предложил следующую задачку:
Найти сумму всех натуральных чисел от 1 до 100.
Юный Гаусс справился с этим заданием достаточно быстро, найдя интересную закономерность, которая получила большое распространение и применяется по сей день при устном счете.
Давайте попробуем решить эту задачку устно. Но для начала возьмем числа от 1 до 10:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
Посмотрите внимательно на эту сумму и попробуйте догадаться, что же необычного смог разглядеть Гаусс? Для ответа необходимо хорошо представлять себе состав чисел.
Гаусс сгруппировал числа следующим образом:
(1+10) + (2+9) + (3+8) + (4+7) + (5+6)
Таким образом маленький Карл получил 5 пар чисел, каждая из которых в отдельности в сумме дает 11. Тогда, чтобы вычислить сумму натуральных чисел от 1 до 10 необходимо
Вернемся к первоначальной задаче. Гаусс заметил, что перед суммированием необходимо группировать числа в пары и тем самым изобрел алгоритм, благодаря которому можно быстро сложить числа от 1 до100:
1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100
Находим количество пар в ряде натуральных чисел. В данном случае их 50.
Суммируем первое и последнее числа данного ряда. В нашем примере — это 1 и 100. Получаем 101.
Умножаем полученную сумму первого и последнего члена ряда на количество пар этого ряда. Получаем 101 * 50 = 5050
Следовательно, сумма натуральных чисел от 1 до 100 равна 5050.
Видео:Сумма чисел от 1 до 100. Секрет ГауссаСкачать

Задачи на использование правила Гаусса
А сейчас вашему вниманию предлагаются задачи, в которых в той или иной степени используется правило Гаусса. Эти задачки вполне способен понять и решить четвероклассник.
Можно дать возможность ребенку порассуждать самому, чтобы он сам «изобрел» это правило. А можно разобрать вместе и посмотреть как он сможет его применить. Среди ниже приведенных задач есть примеры, в которых нужно понять как модифицировать правило Гаусса, чтобы его применить к данной последовательности.
В любом случае, чтобы ребенок мог оперировать этим в своих вычислениях необходимо понимание алгоритма Гаусса, то есть умение разбить правильно по парам и посчитать.
Важно! Если будет заучена формула без понимания, то это очень быстро будет забыто.
Задача 1
Найти сумму чисел:
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10;
- 1 + 2 + 3 + … + 14 + 15 + 16;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9;
- 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100.
Вначале можно дать возможность ребенку самому решить первый пример и предложить найти способ, при котором это сделать легко в уме. Далее разобрать этот пример вместе с ребенком и показать как это сделал Гаусс. Лучше всего для наглядности записать ряд и соединить линиями пары чисел, дающие в сумме одинаковое число. Важно, чтобы ребенок понял как образуются пары — берем самое маленькое и самое большое из оставшихся чисел при условии, что количество чисел в ряду четно.
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = (1 + 10) + (2 + 9) + (3 + 8) + (4 + 7) + (5 + 6) = (1 + 10) * 5;
- 1 + 2 + 3 + … + 14 + 15 + 16 = (1 + 16) + (2 + 15) + (3 + 14) + (4 + 13) + (5 + 12) + (6 + 11) + (7 + 10) + (8 + 9) = (1 + 16) * 8 = 136;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) + (2 + 7) + (3 + 6) + (4 + 5) + 9 = (1+ 8) * 4 + 9 = 45;
- 1 + 2 + 3 + 4 + 5 + … + 48 + 49 + 50 + 51 + 52 + 53 + … + 96 + 97 + 98 + 99 + 100 = (1 + 100) * 50 = 5050
Задача 2
Имеется 9 гирь весом 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г. Можно ли разложить эти гири на три кучки с равным весом?
С помощью правила Гаусса находим сумму всех весов:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = (1 + 8) * 4 + 9 = 45 (г)
Далее смотрим, можно ли этот вес разбить на три равных веса:
Значит, если мы сможем сгруппировать гири так, чтобы в каждой кучке были гири суммарным весом 15г, то задача решена.
Один из вариантов:
Другие возможные варианты найдите сами с ребенком.
Обратите внимание ребенка на то, что когда решаются подобные задачи лучше всегда начинать группировать с большего веса (числа).
Задача 3
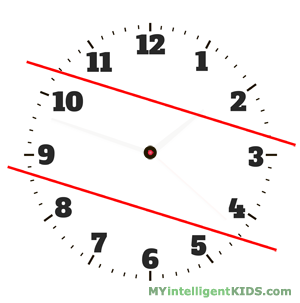
Можно ли разделить циферблат часов прямой линией на две части так, чтобы суммы чисел в каждой части были равны?
Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим, делится ли она на 2:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78
Значит разделить можно. Теперь посмотрим как.
По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:
1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.
Следовательно, надо провести линию на циферблате так, чтобы 3 пары попали в одну половину, а три в другую.
Ответ: линия пройдет между числами 3 и 4, а затем между числами 9 и 10.
Задача 4
Можно ли провести на циферблате часов две прямые линией так, чтобы в каждой части сумма чисел была одинаковой?
Для начала к ряду чисел 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 применим правило Гаусса: найдем сумму и посмотрим делиться ли она на 3:
1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 + 12 = (1 + 12) * 6 = 78
78 делиться на 3 без остатка, значит разделить можно. Теперь посмотрим как.
По правилу Гаусса у нас получается 6 пар чисел, каждая из которых в сумме дает 13:
1 и 12, 2 и 11, 3 и 10, 4 и 9, 5 и 8, 6 и 7.
Следовательно, надо провести линии на циферблате так, чтобы в каждую часть попали по 2 пары.
Ответ: первая линия пройдет между числами 2 и 3, а затем между числами 10 и 11; вторая линия — между числами 4 и 5, а затем между 8 и 9.
Задача 5
Летит стая птиц. Впереди одна птица (вожак), за ней две, потом три, четыре и т. д. Сколько птиц в стае, если в последнем ряду их 20?
Получаем, что нам необходимо сложить числа от 1 до 20. А к вычислению такой суммы можно применить правило Гаусса:
1 + 2 + 3 + 4 + 5 + … + 15 + 16 + 17 + 18 + 19 + 20 = (20 + 1) * 10 = 210.
Задача 6
Как рассадить 45 кроликов в 9 клеток так, чтобы во всех клетках было разное количество кроликов?
Если ребенок решил и с пониманием разобрал примеры из задания 1, то тут же вспоминается, что 45 это сумма чисел от 1 до 9. Следовательно, сажаем кроликов так:
- первая клетка — 1,
- вторая — 2,
- третья — 3,
- …
- восьмая — 8,
- девятая — 9.
Но если ребенок сразу не может сообразить, то попробуйте натолкнуть его на мысль о том, что подобные задачи можно решить перебором и надо начинать с минимального числа.
Задача 7
Вычислить сумму, используя прием Гаусса:
- 31 + 32 + 33 + … + 40;
- 5 + 10 + 15 + 20 + … + 100;
- 91 + 81 + … + 21 + 11 + 1;
- 1 + 2 + 3 + 4 + … + 18 + 19 + 20;
- 1 + 2 + 3 + 4 + 5 + 6;
- 4 + 6 + 8 + 10 + 12 + 14;
- 4 + 6 + 8 + 10 + 12;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11.
- 31 + 32 + 33 + … + 40 = (31 + 40) * 5 = 355;
- 5 + 10 + 15 + 20 + … + 100 = (5 + 100) * 10 = 1050;
- 91 + 81 + … + 21 + 11 + 1 = (91 + 1) * 5 = 460;
- 1 + 2 + 3 + 4 + … + 18 + 19 + 20 = (1 + 20) * 10 =210;
- 1 + 2 + 3 + 4 + 5 + 6 = (1 + 6) * 3 = 21;
- 4 + 6 + 8 + 10 + 12 + 14 = (4 + 14) * 3 = 54;
- 4 + 6 + 8 + 10 + 12 = (4 + 10) * 2 + 12 = 40;
- 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 + 11 = (1 + 10) * 5 + 11 = 66.
Задача 8
Имеется набор из 12 гирек массой 1г, 2г, 3г, 4г, 5г, 6г, 7г, 8г, 9г, 10г, 11г, 12г. Из набора убрали 4 гирьки, общая масса которых равна трети общей массы всего набора гирек. Можно ли оставшиеся гирьки расположить на двух чашках весов по 4 штуки на каждой чашке так, чтобы они оказались в равновесии?
Применяем правило Гаусса, чтобы найти общую массу гирек:
1 + 2 + 3 + … + 10 + 11 + 12 = (1 + 12) * 6 = 78 (г)
Вычисляем массу гирек, которые убрали:
Следовательно, оставшиеся гирьки (общей массой 78-26 = 52г) надо расположить по 26 г на каждую чашу весов, чтобы они оказались в равновесии.
Нам не известно какие гирьки были убраны, значит мы должны рассмотреть все возможные варианты.
Применяя правило Гаусса можно разбить гирьки на 6 пар с равным весом (по 13г):
1г и 12г, 2г и 11г, 3г и 10, 4г и 9г, 5г и 8г, 6г и 7г.
Тогда лучший вариант, когда при убирании 4 гирек уберутся две пары из приведенных выше. В этом случае у нас останутся 4 пары: 2 пары на одну чашу весов и 2 пары на другую.
Худший вариант — это когда 4 убранные гирьки разобьют 4 пары. У нас останутся 2 неразбитые пары общим весом 26г, значит их помещаем на одну чашу весов, а оставшиеся гирьки можно поместить на другую чашу весов и они тоже будут 26г.
Видео:Сумма чисел от 1 до 100Скачать

Уравнение гаусса от 1 до 100
Однажды десятилетний мальчик по имени Карл поставил в тупик своего учителя арифметики, решив очень трудную задачу за считанные секунды. В будущем Карл стал одним из величайших ученых, заслужив неофициальный титул “Короля математики”. А все началось с этого маленького открытия в школе. Так что же придумал Карл?
Дело было так. Учитель решил занять детей и заодно немного отдохнуть. Он задал классу, по его мнению, очень трудное задание. Задание было следующим: посчитайте сумму всех чисел от 1 до 100. Как бы вы посчитали такую сумму?
В те времена, такие задачи решали методом “в лоб”: долго и нудно складывая все числа от 1 до 100.
1+2=3, 3+3=6, 6+4=10 и так далее. И пока дети решали бы задачу, «грызли гранит науки», учитель надеялся немного отдохнуть. В зависимости от навыков сложения, кто-то справлялся быстрее, а кто-то медленнее, кто-то получал верный ответ, а кто-то — нет.
Каково же было удивление учителя, когда спустя всего несколько секунд, десятилетний Карл поднялся со своей скамьи, уверенным шагом прошел к учительскому столу и выложил на него листок бумаги, со словами: “вот решение”. Карл показал листок, на котором было написано лишь одно число — 5050. Учитель не поверил, что возможно так быстро решить задачу и подумал, что паренек хочет над ним подшутить. Согласно легенде, мальчик за это получил нехилую взбучку (был такой варварский обычай в школах тех времен).
Но ответ был правильный и на вопрос учителя, о том, как Карлу удалось так быстро найти решение, мальчик ответил, что заметил закономерность. Сумма первого и последнего числа 1 и 100 равна 101, сумма второго и предпоследнего числа — 2 и 99 также равна 101. Карл заметил, что это справедливо для всех пар чисел заканчивая последней парой — 50 и 51. И всего таких пар от 1 до 100 было 50. Таким образом, Карлу Гауссу осталось посчитать 50 раз по 101, иначе говоря, умножить 50 на 101 и получить конечный ответ- 5050!
Попробуем усложнить задачу. Предположим, что нам нужно посчитать сумму всех цифр от 1 до n, где n-любое натуральное число (их еще называют естественными числами, возникающими естественным образом при счете).
Получится ли решить такую задачу способом Гаусса? Оказывается, что да. Для удобства предположим, что число n четное, так как сама постановка задачи о делении всех чисел на пары подразумевает, что их четное количество.
Заметьте, что сумма каждой пары равна n+1 и что количество таких пар n/2. Нам остается лишь перемножить сумму каждой пары (n+1) на количество пар (n/2) по аналогии c задачей, с которой столкнулся Карл. Обозначим сумму буквой S.
S=(n+1)*n/2 (при условии, что n — четное натуральное число).
А что если n — нечетное число, что делать тогда?
Или первое число не равно единице?
Или разница между соседними числами не один, а скажем три?
Или нам нужно посчитать такую сумму:
И единственное, что их объединяет с числами, которые суммировал Карл — это закономерность, связывающая соседние элементы между собой. Каждый следующий элемент получается из предыдущего путем прибавления одного и того же числа. Обозначим это общее для всей последовательности число как d и a n=a(n-1) + d. Таким образом, каждый элемент последовательности можно представить так:
Мы только что дали определение арифметической прогрессии и d — разность прогрессии.
Последовательность — упорядоченный список элементом, в данном случае в качестве элементов выступают числа.
Оказывается логика, которой руководствовался Гаусс, верна и в этом случае. Для того чтобы это показать, нам нужно слегка модифицировать трюк Карла и разбить пары несколько иначе. Помня, что от перестановки мест слагаемых сумма не меняется, обозначим сумму такой последовательности как S и запишем ее двумя зеркально разными способами.
Прибавим оба равенства, последовательно прибавляя в правой части слагаемые, которые стоят на одной вертикали. Так вот все эти пары равны между собой. Как бы вы это показали? Я думаю, что наш друг Карл заметил бы особенность таких пар: если начинать с первой пары (a 1+an), то в каждой следующей паре первое слагаемое пары увеличивается на d, тогда как второе уменьшается на d и, в конечном счете, сумма не меняется и равна (a1+an). Учитывая, что таких пар n делим обе части равенства на два, получаем:
Получаем формулу суммы арифметической прогрессии. Если вспомнить, что любой элемент прогрессии выражается через первый элемент a1 и разность прогрессии — d, то можно переписать формулу суммы следующим образом:
Видео:Как за 10 секунд найти сумму всех натуральных чисел от 1 до 100Скачать

Уравнение гаусса от 1 до 100
Учитель: Запишите тему урока: метод Гаусса. Вы сегодня узнаете кто такой Гаусс и что такое метод Гаусса и как его можно применить.
В истории математики известен такой случай. Однажды, а было это в Германии, в конце 18 в., для того чтобы заставить учеников поработать, учитель дал им задание подсчитать сумму всех натуральных чисел от 1 до 100. Какова же было его удивление, когда уже через несколько минут один ученик сказал ему ответ: искомая сумма равна 5050! Этот ученик, Карл Фридрих Гаусс, а ему было тогда 10 лет, стал одним из великих математиков мира. Как же маленькому Гауссу удалось быстро подсчитать сумму? Запишите в тетради: Карл Гаусс, 18в, Германия . Чтобы понять, как рассуждал Гаусс, разберем задачу
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |