Уравнение гармонической волны распространяющейся в упругой среде назовите ее параметры

«Физика — 11 класс»

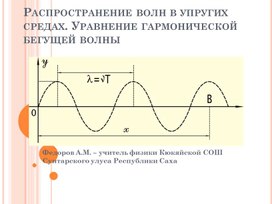
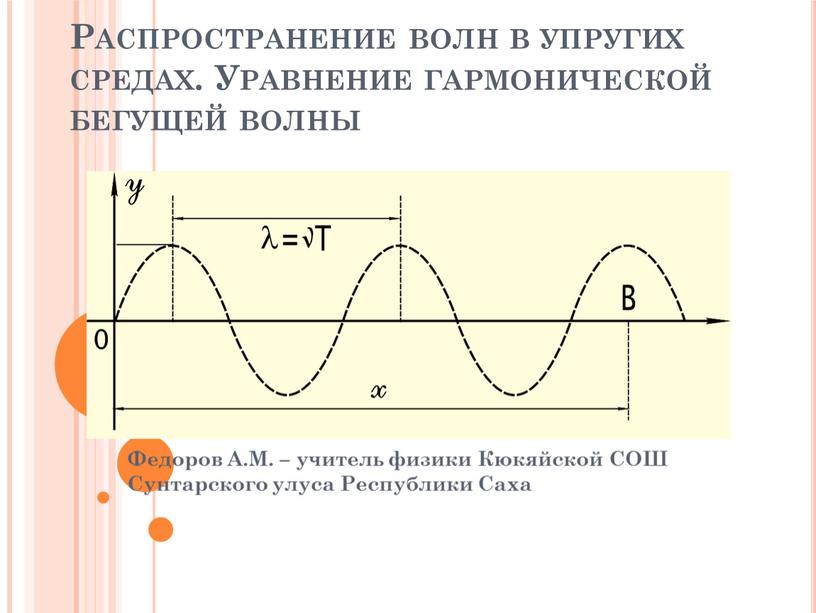
Длина волны. Скорость волны

За один период волна распространяется на расстояние λ.

λ = vT

Длина волны — это расстояние, на которое распространяется волна за время, равное одному периоду колебаний.

Так как период Т и частота v связаны соотношением

При распространении волны:

1. Каждая частица шнура совершает периодические колебания во времени.
В случае гармонических колебаний (по закону синуса или косинуса) частота и амплитуда колебаний частиц одинаковы во всех точках шнура.
Эти колебания различаются только фазами.

2. В каждый момент времени форма волны повторяется через отрезки длиной λ.

Спустя промежуток времени Δt волна будет иметь вид, изображенный на том же рисунке второй линией.

Для продольной волны также справедлива формула, связывающая скорость распространения волны, длину волны и частоту колебаний.

Все волны распространяются с конечной скоростью. Длина волны зависит от скорости ее распространения и частоты колебаний.

Уравнение гармонической бегущей волны

Вывод уравнения волны, позволяющего определить смещение каждой точки среды в любой момент времени при распространении гармонической волны (на примере поперечной волны, бегущей по длинному тонкому резиновому шнуру).

Ось ОХ направлена вдоль шнура.
Начало отсчета — левый конец шнура.
Смещение колеблющейся точки шнура от положения равновесия — s.
Для описания волнового процесса нужно знать смещение каждой точки шнура в любой момент времени:

s = s (х, t).

Конец шнура (точка с координатой х = 0) совершает гармонические колебания с циклической частотой ω.
Колебания этой точки будут происходят по закону:

s = s_m sinc ωt

Если начальную фазу колебаний считать равной нулю.
s_m — амплитуда колебаний.

Колебания распространяются вдоль оси ОХ со скоростью υ и в произвольную точку с координатой х придут спустя время

Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ.

Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой s_m, но с другой фазой:

Это и есть уравнение гармонической бегущей волны, распространяющейся в положительном направлении оси ОХ.

Используя уравнение можно определить смещение различных точек шнура в любой момент времени.

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Механические волны. Физика, учебник для 11 класса — Класс!ная физика

Видео:Тема 6. Распространение колебаний в упругой среде. Волны. Частота, длина, скорость распространенияСкачать

Презентация к уроку физики в 11 классе «Распространение волн в упругих средах. Уравнение гармонической бегущей волны»

Видео:Распространение волн в упругих средах. Звуковые волны | Физика 11 класс #18 | ИнфоурокСкачать

Распространение волн в упругих средах

Распространение волн в упругих средах. Уравнение гармонической бегущей волны

Федоров А.М. – учитель физики Кюкяйской СОШ Сунтарского улуса Республики Саха

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Бегущая волна Выведем уравнение волны, которое позволит определить смещение каждой точки среды в любой момент времени при распространении гармонической волны

Выведем уравнение волны, которое позволит определить смещение каждой точки среды в любой момент времени при распространении гармонической волны. Сделаем это на примере волны, бегущей по длинному тонкому резиновому шнуру.
Ось ОХ направим вдоль шнура, а начало отсчета свяжем с левым концом шнура. Смещение колеблющейся точки шнура от положения равновесия обозначим буквой s. Для описания волнового процесса нужно знать смещение каждой точки шнура в любой момент времени. Следовательно, надо знать вид функции
s = s (х, t).
Заставим конец шнура (точка с координатой х = 0) совершать гармонические колебания с циклической частотой ω. Колебания этой точки будут происходить по закону:
s = sm sin ωt, (6.3)
если начальную фазу колебаний считать равной нулю. Здесь sm — амплитуда колебаний (рис. 6.10, а).

Видео:Упругие механические волны. 1 часть. 11 класс.Скачать

Уравнение бегущей волны Колебания распространяются вдоль шнура (оси

Уравнение бегущей волны

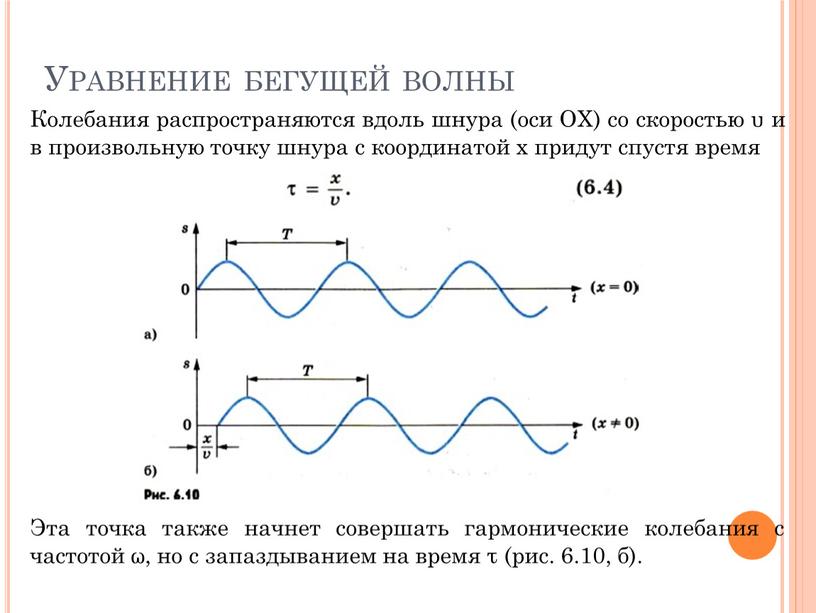
Колебания распространяются вдоль шнура (оси ОХ) со скоростью υ и в произвольную точку шнура с координатой х придут спустя время

Эта точка также начнет совершать гармонические колебания с частотой ω, но с запаздыванием на время τ (рис. 6.10, б).

Видео:Урок 95 (осн). Механические волны. ЗвукСкачать

Уравнение бегущей волны Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой sm, но с…

Уравнение бегущей волны

Если пренебречь затуханием волны по мере ее распространения, то колебания в точке х будут происходить с той же амплитудой sm, но с другой фазой:

Это и есть уравнение гармонической бегущей волны, распространяющейся в положительном направлении оси ОХ.
Волна при распространении от какого-либо источника в сплошной среде постепенно захватывает все более обширные области пространства.
Энергия, которую несут с собой волны, с течением времени распределяется по все большей и большей поверхности. Поэтому энергия, переносимая через поверхность единичной площади за одну секунду, уменьшается по мере удаления от источника волн. Следовательно, уменьшается и амплитуда колебаний частиц среды по мере удаления от источника.
Ведь энергия колеблющегося тела пропорциональна квадрату амплитуды его колебаний. Это справедливо для колебаний не только груза на пружине или какого- нибудь другого маятника, но и для любой частицы среды.

Видео:Физика 11 класс (Урок№2 - Механические волны.)Скачать

Плоская волна. Волновая поверхность и луч

Плоская волна. Волновая поверхность и луч

Исключение составляет так называемая плоская волна. Такую волну можно получить, если поместить в упругую среду большую пластину и заставить ее колебаться в направлении нормали к пластине. Все точки среды, примыкающие к пластине с одной стороны, будут совершать колебания с одинаковыми амплитудами и фазами. Эти колебания будут распространяться в виде волн в направлении нормали к пластине, причем все частицы среды, лежащие в плоскости, параллельной пластине, будут колебаться в одной фазе. Поверхность равной фазы называется волновой поверхностью.
В случае плоской волны волновые поверхности представляют собой плоскости (рис. 6.11). Так как все точки, принадлежащие одной волновой поверхности, колеблются одинаково, то уравнение плоской бегущей волны будет иметь вид

где s — смещение всех точек волновой поверхности в данный момент времени, а ось X совпадает с направлением распространения волны и, соответственно, перпендикулярна волновой поверхности.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Распространение плоской волы Линия, нормальная к волновой поверхности, называется лучом

Распространение плоской волы

Линия, нормальная к волновой поверхности, называется лучом. Под направлением распространения волн понимают направление именно лучей. Лучи для плоских волн представляют собой параллельные прямые (см. рис. 6.11). Вдоль лучей происходит перенос энергии.
При распространении плоской волны размеры волновых поверхностей по мере удаления от пластины не меняются (или почти не меняются). Поэтому энергия волны не рассеивается в пространстве и амплитуда колебаний частиц среды уменьшается только за счет действия сил трения.
На поверхности воды легко получить линейные волны, которые дают наглядное представление о плоских волнах в пространстве. Для этого нужно стержень, слегка касающийся поверхности воды, заставить колебаться в направлении, перпендикулярном поверхности воды.
Все частицы воды, находящиеся на прямой, параллельной стержню, будут колебаться в одинаковой фазе (рис. 6.12).

Видео:Распространение колебаний в среде. Волны | Физика 9 класс #28 | ИнфоурокСкачать

Фронт волны Фронтом волны называется геометрическое место точек, до которых дошли возмущения в данный момент времени

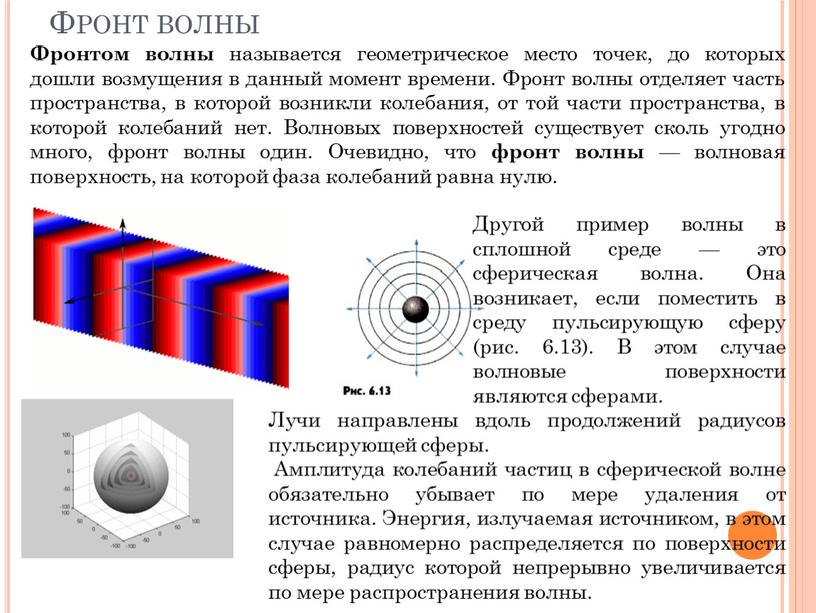
Фронтом волны называется геометрическое место точек, до которых дошли возмущения в данный момент времени. Фронт волны отделяет часть пространства, в которой возникли колебания, от той части пространства, в которой колебаний нет. Волновых поверхностей существует сколь угодно много, фронт волны один. Очевидно, что фронт волны — волновая поверхность, на которой фаза колебаний равна нулю.

Другой пример волны в сплошной среде — это сферическая волна. Она возникает, если поместить в среду пульсирующую сферу (рис. 6.13). В этом случае волновые поверхности являются сферами.
Лучи направлены вдоль продолжений радиусов пульсирующей сферы.
Амплитуда колебаний частиц в сферической волне обязательно убывает по мере удаления от источника. Энергия, излучаемая источником, в этом случае равномерно распределяется по поверхности сферы, радиус которой непрерывно увеличивается по мере распространения волны.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Упражнения Задача1. уравнение бегущей волны имеет вид

Задача1.уравнение бегущей волны имеет вид

Найдите частоту волны, скорость её распространения и длину.
Задача 2. В воздухе звук проходит 1,1 км на 2,6 с медленнее, чем в воде. Принимая скорость звука в воздухе равной 330 м/с, определите скорость звука в воде.
Задача 3. Два человека бросают разные камни в воду на разное расстояние от берега, но волны приходят к берегу одновременно. Расстояние между двумя ближайшими гребнями волны от первого камня равно 2 см, а расстояние между двумя ближайшими гребнями волны от второго камня — 2,5 см. Найдите соотношение расстояний, на которые были брошены камни, если известно, что обе волны имеют одинаковую частоту.
Задача 4. Бегущая по шнуру волна распространяется со скоростью 30 см/с. Известно, что в момент времени t = 2 с центральная точка шнура в первый раз отклоняется от положения равновесия в положительном направлении на максимальное расстояние. Найдите длину шнура, если длина бегущей волны равна 2 см.

Видео:Якута А. А. - Механика - Волновое уравнение. Механические волны. Скорость распространения волнСкачать

КИНЕМАТИКА ВОЛНОВЫХ ПРОЦЕССОВ

Видео:Физика 9 класс. §28 Распространение колебаний в среде. ВолныСкачать

ВОЛНЫ В УПРУГОЙ СРЕДЕ. УРАВНЕНИЕ ВОЛНЫ

Тело называют упругим или сплошным, а его деформации от внешнего воздействия — упругими, если деформации тела исчезают с прекращением воздействий. Согласно закону Р. Гука упругие деформации определяются внешними воздействиями. Для объемной деформации, например, газа изменение его давления dP при бесконечно малом изменении объема dV прямо пропорционально относительной объемной деформации: dP = — kdV / V, Па, где к — модуль объемной упругости газа, Па. Твердые тела, помимо объемной упругости, обладают упругостью формы, которая проявляется в сопротивлении деформации сдвига. Сдвигом называют деформацию твердого тела, при которой все его плоские слои, параллельные некоторой неподвижной плоскости, называемой плоскостью сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу. Деформация твердого тела связана с деформацией его кристаллической решетки. Этим деформациям препятствуют силы взаимодействия между микрочастицами. Упругость жидкости обусловлена тоже силами межмолекулярного взаимодействия. Но, поскольку средняя продолжительность оседлого существования молекул жидкости незначительна, жидкости, подобно газам, обладают только объемной упругостью. Периодический во времени и пространстве процесс распространения деформаций в упругой среде называют волновым процессом, или волной. При распространении волны частицы среды совершают вынужденные колебания. Близко расположенные к источнику возмущений частицы стремятся возвратиться под действием упругих сил межатомного взаимодействия в положение равновесия, а более удаленные частицы выводятся из положений равновесия. Последние взаимодействуют с соседними частицами и т.д. Таким образом, более удаленные от растягиваемого или сжимаемого тела области среды вовлекаются в колебательное движение. Результирующее смещение распространяется в среде в виде импульса — волны. Источники упругих деформаций среды называют источниками упругих волн. Особое внимание следует обратить на тот факт, что распространение упругих волн в среде не связано с переносом вещества. Частицы среды не движутся вместе с волной, а колеблются около своих положений равновесия. То есть вместе с волной от частицы к частице среды передается только состояние колебательного движения и его энергия. Следовательно, основным свойством всех волн является перенос энергии без переноса вещества. Перенос энергии является динамическим признаком волнового движения, а кинематическим признаком волнового движения служит распространение фазы колебаний.

Волны классифицируются на упругие, волны на поверхности жидкости и электромагнитные. Волны бывают продольными и поперечными. Упругая волна называется продольной, если смещение каждой частицы среды происходит вдоль одной линии с направлением распространения волны. Именно так распространяется звук. Продольные волны возникают от деформаций сжатия и расширения упругой среды и могут распространяться в твердой, жидкой и газообразной среде. При забивании гвоздя молотком продольный импульс (волна) высокой плотности проносится вдоль гвоздя, загоняя его конец глубже в дерево.

Упругая волна называется поперечной, если частицы среды колеблются в плоскостях, перпендикулярных направлению распространения волны. Поперечные волны возникают от деформаций сдвига только в твердых телах. Такой эффект наблюдается, например, когда резким боковым движением посылается импульс вдоль веревки. Поперечно также электромагнитное излучение. Волны на воде обычно представляют собой смесь продольных и поперечных волн. Каждая отдельная капля, возбужденная проходящей волной, совершает движение по эллипсу, перемещаясь вверх и вниз, вперед и назад.

По характеру распространения различают линейные, поверхностные и пространственные, или одно-, двух- и трехмерные волны. Границу, отделяющую колеблющиеся частицы от частиц, еще не начавших колебаться, называют фронтом волны. Все частицы волнового фронта колеблются с одинаковой фазой. Волновой фронт перпендикулярен лучу. Под лучом понимают направление распространения волны. Упругую волну называют гармонической или синусоидальной, если колебания составляющих ее частиц являются гармоническими.

Независимо от продольного или поперечного характера волнового движения смещение каждой отдельной частицы в упругой среде можно выразить в виде функции времени. На рис. 15.1 представлена зависимость между смещением %(х, t) частиц среды, участвующих в волновом процессе, и расстоянием х этих частиц от источника колебаний для фиксированного момента времени t, с. Таким образом, график волны выражает зависимости смещения всех частиц среды от расстояния до источника колебаний в данный момент времени. Вспомним, что график колебаний дает зависимость смещения данной частицы от времени. Для частицы В (см. рис. 15.1), запаздывающей в своем колебании на время распространения колебаний от 0 до В, равное х = х/ v, уравнение волны имеет вид

или

Любое из уравнений позволяет определить смещение любой точки волны в любой момент времени и называется уравнением волны. Здесь Л — амплитуда волны, м; со = 2тг / Т — циклическая (круговая) частота волны, рад/с; Т — период колебаний, с; со/ — сох / v + + ф₀ = со/ — кх + ср₀ — фаза плоской волны, равная фазе колебаний в произвольной точке с координатой х, рад; ср₀ — начальная фаза колебаний в точках координатной плоскости х = О, рад; v/v = vT=X — длина волны — расстояние между ближайшими частицами, колеблющимися в одинаковой фазе, м; к = 2п / X = 2к / (vT) = со / v — волновое число, указывает сколько длин волн укладывается на отрезке длиной 2к, рад/м.

Распространение волн в изотропной среде в общем виде описывается волновым уравнением

где V 2 = —тН—тН—т — оператор Лапласа.

Для плоской волны вдоль оси х волновое уравнение становится одномерным:

🔍 Видео

Урок 327. Гармонические колебанияСкачать

Урок 370. Механические волны. Математическое описание бегущей волныСкачать

Выполнялка 53.Гармонические колебания.Скачать

Физика. 11 класс. Упругие механические волны. Уравнение бегущей и стоячей волны /16.11.2020/Скачать

74. Упругие волныСкачать

Физика Волна распространяется в упругой среде со скоростью 2000 м/с. Найдите частоту колебаний точекСкачать

Волны. Основные понятия. Решение задач.Задача 1Скачать

Консультация к устному экзамену. Механика. Часть 9: "Волны"Скачать

Упругие механические волны. 2 часть. 11 класс.Скачать