Уравнение гармонических колебаний по закону sin

Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

I. Механика

Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Тестирование онлайн

Видео:5.4 Уравнение гармонических колебанийСкачать

Гармоническое колебание

Это периодическое колебание, при котором координата, скорость, ускорение, характеризующие движение, изменяются по закону синуса или косинуса.

Видео:Урок 327. Гармонические колебанияСкачать

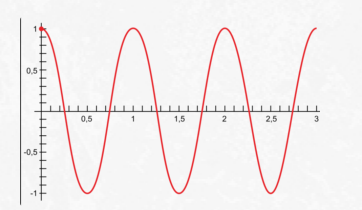
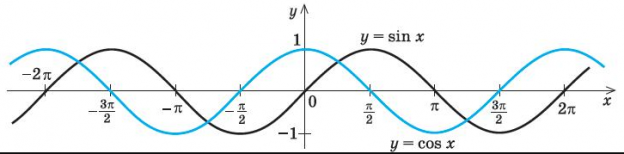
График гармонического колебания

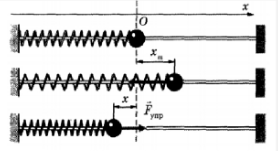
График устанавливает зависимость смещения тела со временем. Установим к пружинному маятнику карандаш, за маятником бумажную ленту, которая равномерно перемещается. Или математический маятник заставим оставлять след. На бумаге отобразится график движения.

Графиком гармонического колебания является синусоида (или косинусоида). По графику колебаний можно определить все характеристики колебательного движения.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Уравнение гармонического колебания

Уравнение гармонического колебания устанавливает зависимость координаты тела от времени

График косинуса в начальный момент имеет максимальное значение, а график синуса имеет в начальный момент нулевое значение. Если колебание начинаем исследовать из положения равновесия, то колебание будет повторять синусоиду. Если колебание начинаем рассматривать из положения максимального отклонения, то колебание опишет косинус. Или такое колебание можно описать формулой синуса с начальной фазой .

Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Изменение скорости и ускорения при гармоническом колебании

Не только координата тела изменяется со временем по закону синуса или косинуса. Но и такие величины, как сила, скорость и ускорение, тоже изменяются аналогично. Сила и ускорение максимальные, когда колеблющееся тело находится в крайних положениях, где смещение максимально, и равны нулю, когда тело проходит через положение равновесия. Скорость, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия — достигает максимального значения.

Если колебание описывать по закону косинуса

Если колебание описывать по закону синуса

Видео:Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Видео:Выполнялка 53.Гармонические колебания.Скачать

Как получить зависимости v(t) и a(t)

Формулы зависимостей скорости от времени и ускорения от времени можно получить математически, зная зависимость координаты от времени. Аналогично равноускоренному движению, зависимость v(t) — это первая производная x(t). А зависимость a(t) — это вторая производная x(t).

При нахождении производной предполагаем, что переменной (то есть x в математике) является t, остальные физические величины воспринимаем как постоянные.

Видео:Урок 335. Анализ графика гармонических колебанийСкачать

Гармонические колебания

теория по физике 🧲 колебания и волны

Гармоническими законами называют законы синуса и косинуса. Следовательно, гармоническими колебаниями называют те колебания, при которых координата тела изменяется синусоидально или косинусоидально.

Гармонические колебания — колебания, при которых координата тела изменяется с течением времени по гармоническому закону.

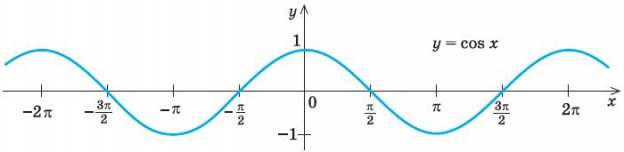
Ниже представлен график косинусоидальной функции. Обратите внимание, что косинус при возрастании аргумента от нуля сначала меняется медленно, а потом он все быстрее и быстрее приближается к нулю. Пройдя через него, его модуль снова быстро возрастает. Но по мере приближения к максимальному значению он снова замедляется. Точно так же меняются координаты свободно колеблющегося тела.

Важно! Гармоническими можно считать только те колебания, что совершаются грузом, закрепленном на пружине, или математическим маятником, отклоняемым на малый угол, при котором ускорение тела пропорционально его смещению.

Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ И ВОЛНЫСкачать

Уравнение движения гармонических колебаний

Известно, что ускорение колеблющегося на пружине груза пропорционально его смещению от положения равновесия:

Также известно, что ускорение есть вторая производная координаты. Следовательно, при свободных колебаниях координата изменяется со временем так, что вторая производная координаты по времени прямо пропорциональна самой координате и противоположна ей по знаку.

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x″ = − x m a x cos . t = − x

Видно, что в этом случае теряется величина k m . . , служащая постоянной для каждой колебательной системы. Чтобы получить ее во второй производной, нужно усложнить функцию до следующего вида:

x = x m a x cos . √ k m . . t

Тогда первая производная примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x′ = − √ k m . . x m a x sin . √ k m . . t

Вторая производная примет вид:

x″ = − k m . . x m a x cos . √ k m . . t = − k m . . x

Так как мы получили ровно такое же выражение, то описать свободные колебания можно уравнениями следующего вида:

x = x m a x sin . √ k m . . t

x = x m a x cos . √ k m . . t

Обозначим постоянную величину √ k m . . , зависящую от свойств системы, за ω₀:

x = x m a x sin . ω 0 t

x = x m a x cos . ω 0 t

Само уравнение движения, описывающего свободные колебания, примет вид:

Видео:Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Период и частота гармонических колебаний

Минимальный промежуток времени T, через который движение тела полностью повторяется, называют периодом колебания. Зная его, можно вычислить частоту колебаний, равную числу колебаний в единицу времени. Эти величины связаны между собой выражением:

Через промежуток времени, равный периоду T и соответствующий изменению аргумента косинуса на ω 0 T , движение тела повторяется, и косинус принимает прежнее значение. Но из математики известно, что наименьший период косинуса равен 2π. Следовательно:

ω 0 = 2 π T . . = 2 π ν

Таким образом, величина ω 0 представляет собой число колебаний тела, но не за 1 секунду, а за 2 π секунд. Эта величина называется циклической (круговой) частотой. А частоту свободных колебаний называют собственной частотой колебательной системы.

Видео:Гармонические колебанияСкачать

Зависимость частоты и периода свободных колебаний от свойств системы

Изначально за величину ω 0 мы принимали постоянную, характеризующую свойства системы:

Теперь мы выяснили, что циклическая частота связана с периодом и частотой колебаний. Следовательно, период и частота колебаний также зависят от свойств системы:

ω 0 = √ k m . . = 2 π T . . = 2 π ν

Отсюда период и частота колебаний соответственно равны:

T = 2 π ω 0 . . = 2 π √ m k . .

ν = 1 2 π . . √ k m . .

Вспомним, что свойства колебательной системы математического маятника определяются постоянной величиной g l . . . Следовательно, циклическая частота для него равна:

Отсюда период и частота колебаний математического маятника соответственно равны:

T = 2 π ω 0 . . = 2 π √ l g . .

ν = 1 2 π . . √ g l . .

Эта формула была впервые получена и проверена на опыте голландским ученым Г. Гюйгенсом, современником И. Ньютона.

Период колебания возрастает с увеличением длины маятника. От массы маятника он не зависит. Это легко проверить на опыте с различными маятниками. Зависимость периода от ускорения свободного падения также легко прослеживается. Чем меньше величина g, тем больше период колебания маятника, и, следовательно, тем медленнее идут часы с маятником. Так, часы с маятником в виде груза на стержне отстанут в сутки почти на 3 с, если их поднять из подвала на верхний этаж Московского университета, который находится на высоте 200 м. И это только за счет уменьшения ускорения свободного падения с высотой.

Зависимость периода колебаний маятника от значения g используется на практике. Измеряя период колебания, можно легко измерить g. Ускорение свободного падения меняется с географической широтой. Но и на данной широте оно неодинаково, так как плотность земной коры неоднородна. В районах, где залегают более плотные породы, ускорение свободного падения принимает большие значения.

Пример №1. Сколько колебаний совершает математический маятник длиной 4,9 м за время 5 минут?

Искомое число колебаний равно отношению времени к периоду колебаний:

Период колебаний для математического маятника определяется формулой:

N = t 2 π . . √ g l . . = 300 2 · 3 , 14 . . √ 9 , 8 4 , 9 . . ≈ 68

Видео:10 класс, 19 урок, График гармонического колебанияСкачать

Фаза колебаний

При заданной амплитуде гармонических колебаний координата колеблющегося тела в любой момент времени однозначно определяется аргументом косинуса или синуса, который равен ω 0 t . Обозначим его за ϕ и получим:

Величину ϕ, стоящую под знаком косинуса или синуса, называют фазой колебаний, описываемой этой функцией. Выражается фаза в угловых единицах — радианах (рад).

Фаза определяет значение не только координаты, но и других физических величин (к примеру, скорости и ускорения, которые также изменяются по гармоническому закону). Отсюда можно сделать вывод, что фаза определяет при заданной амплитуде состояния колебательной системы в любой момент времени.

Колебания с одинаковыми частотами и амплитудами могут отличаться друг от друга фазами. Так как ω 0 = 2 π T . . , фаза определяется формулой:

ϕ = ω 0 t = 2 π t T . .

t T . . — отношение, которое указывает, какая часть периода прошла от момента начала колебаний. Любому моменту времени, выраженному в долях периода, соответствует значение фазы, выраженное в радианах. К примеру:

Можно изобразить на графике зависимость координаты колеблющейся точки не от времени, а от фазы. В этом случае графиком также будет являться косинусоида (или синусоида), но аргументом функции будет не время (период), а фаза, выражающаяся в радианах (см. рис.).

Синус от косинуса отличается только смещением аргумента на π 2 . . (см. рис. ниже). Поэтому для описания гармонических колебаний можно использовать как синусоидальный, так и косинусоидальный закон.

Выбор закона зависит от условий задачи. Если колебания начинаются с того, что тело выводят из положения равновесия и отпускают, удобнее пользоваться косинусоидальным законом, поскольку в начальный момент времени косинусоида показывает, что это тело отклонено максимально, а не находится в положении равновесия. Если для того чтобы начались колебания, совершают толчок, удобнее использовать синусоидальный закон, так как начальному моменту времени на синусоиде соответствует положение равновесия.

Колебания, совершаемые по закону синуса и косинуса, отличаются только фазой, которая смещена на значение, равное π 2 . . . Это значение называют сдвигом фаз, или их разностью. Поэтому косинусоидальная функция также может быть записана как:

x = x m a x cos . ω 0 t = x m a x sin . ( ω 0 t + π 2 . . )

Видео:Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

Превращение энергии при гармонических колебаниях

Чтобы описать превращения энергии при гармонических колебаниях, условимся, что силой трения будем пренебрегать. Для описания обратимся к рисунку ниже.

Точке О на рисунке соответствует положение равновесия шарика. Если его оттянуть на расстояние x_max, равное амплитуде, пружина получит потенциальную энергию, которая примет в этом положении максимальное значение, равное:

W p m a x = k x 2 m a x 2 . .

Когда шарик отпускают, возникает сила упругости, под действием которой шарик устремляется влево. По мере уменьшения расстояния между точкой максимального отклонения и положением равновесия уменьшается и потенциальная энергия. Но в это время увеличивается кинетическая энергия шарика. Когда шарик проходит через положение равновесия в первый раз, его потенциальная энергия становится равной нулю, а кинетическая энергия обретает максимальное значение (скорость в этот момент времени тоже максимальна):

W k m a x = m v 2 m a x 2 . .

После прохождения точки О расстояние между шариком и положением равновесия снова увеличивается, и потенциальная энергия растет. Кинетическая же энергия при этом уменьшается. А в крайнем положении слева она становится равной нулю, в то время как потенциальная энергия снова примет максимальное значение.

Так как мы условились пренебрегать трением, данную колебательную систему можно считать изолированной. Тогда в ней должен соблюдаться закон сохранения энергии. Согласно ему, полная механическая энергия системы равна:

W = W p + W k = k x 2 x 2 . . + m v 2 x 2 . . = k x 2 m a x 2 . . = m v 2 m a x 2 . .

В действительности свободные колебания всегда затухают, так как в колебательной системе действует сила трения. И часть механической энергии рассеивается в виде тепла. Пример графика затухающих колебаний выглядит следующим образом:

Пример №2. Груз, прикрепленный к пружине, колеблется на горизонтальном гладком стержне. Найдите отношение кинетической энергии груза к его потенциальной энергии системы в момент, когда груз находится в точке, расположенной посередине между крайним положением и положением равновесия.

Так как груз находится посередине между крайним положением и положением равновесия, его координата равна половине амплитуды:

В это время потенциальная энергия груза будет равна:

W p = k x 2 2 . . = k ( x m a x 2 . . ) 2 2 . . = k x 2 m a x 8 . .

Согласно закону сохранения энергии, кинетическая энергия в это время равна:

Полная механическая энергия системы равна максимальной потенциальной энергии:

W = W p m a x = k x 2 m a x 2 . .

Тогда кинетическая энергия равна:

W k = k x 2 m a x 2 . . − k x 2 m a x 8 . .

Следовательно, отношение кинетической энергии к потенциальной будет выглядеть так:

W k W p . . = k x 2 m a x 2 . . − k x 2 m a x 8 . . k x 2 m a x 8 . . . . = k x 2 m a x 2 . . 8 k x 2 m a x . . − 1 = 4 − 1 = 3

Видео:Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать

Резонанс

Самый простой способ возбуждения незатухающих колебаний состоит в том, что на систему воздействуют внешней периодической силой. Такие колебания называют вынужденными.

Работы силы над такой системой обеспечивает приток энергии к системе извне. Приток энергии не дает колебаниям затухнуть, несмотря на действие сил трения.

Особый интерес вызывают вынужденные колебаний в системе, способной совершать свободные колебания. Примером такой системы служат качели. Их не получится отклонить на большой угол всего лишь одним толчком. Если их толкать то в одну, то в другую сторону, тоже ничего не получится. Но если подталкивать качели всякий раз, как они сравниваются с нами, можно раскачать их очень сильно. При этом не нужно прикладывать большую силу, но на это понадобится время. Причем после каждого такого толчка амплитуда колебаний качелей будет увеличиваться до тех пор, пока не достигнет своего максимального значения. Такое явление называется резонансом.

Резонанс — резкое возрастание амплитуды вынужденных колебаний при совпадении частоты изменения внешней силы, действующей на систему, с частотой свободных колебаний.

Графически явление резонанса можно изобразить как резкий скачок графика вверх (см. рис. выше). Причем высота «зубца», или амплитуда колебаний, будет зависеть от величины сил трения. Чем больше сила трения, тем меньше при резонансе возрастает амплитуда вынужденных колебаний. Это можно продемонстрировать графиками на рисунке ниже. Графику 1 соответствует минимальное трение, графику 3 — максимальное.

На явлении резонанса основан принцип работы частотомера — устройства, предназначенного для измерения частоты переменного тока. Он состоит из набора упругих пластин, которые закреплены на одной планке. Каждая пластина обладает определенной собственной частотой колебаний, которая зависит от упругих свойств, длины и массы. Собственные колебания пластин известны. Под действием электромагнита планка, а вместе с ней и пластины совершают вынужденные колебания. Но лишь та пластина, собственная частота которой совпадает с частотой колебаний планки, будет иметь большую амплитуду колебаний. Таким образом, определяется частота переменного тока.

Пример №3. Автомобиль движется по неровной дороге, на которой расстояние между буграми равно приблизительно 8 м. Период свободных колебаний автомобиля на рессорах 1,5 с. При какой скорости автомобиля его колебания в вертикальной плоскости станут особенно заметными?

Колебания автомобиля в вертикальной плоскости будут заметны тогда, когда частота наезда на бугры сравняется с частотой свободных колебаний автомобиля на рессорах. Поскольку частота обратно пропорциональна периоду, можно сказать, что резонанс будет достигнут тогда, когда автомобиль будет наезжать на бугры каждые 1,5 секунды. Зная расстояние между буграми и время, можем вычислить скорость:

v = s t . . = 8 1 , 5 . . ≈ 5 , 33 ( м с . . ) ≈ 19 , 2 ( к м ч . . )

Смещение груза пружинного маятника меняется с течением времени по закону x = A cos . 2 π T . . t , где период Т = 1 с. Через какое минимальное время, начиная с момента t = 0, потенциальная энергия маятника вернется к своему исходному значению?

Видео:Гармонические колебания | Физика 11 класс #8 | ИнфоурокСкачать

Если колебание описывать по закону синуса

Максимальные значения скорости и ускорения

Проанализировав уравнения зависимости v(t) и a(t), можно догадаться, что максимальные значения скорость и ускорение принимают в том случае, когда тригонометрический множитель равен 1 или -1. Определяются по формуле

Как получить зависимости v(t) и a(t)

7. Свободные колебания. Скорость, ускорение и энергия колебательного движения. Сложение колебаний

Свободные колебания (или собственные колебания) — это колебания колебательной системы, совершаемые только благодаря первоначально сообщенной энергии (потенциальной или кинети­ческой) при отсутствии внешних воздействий.

Потенциальная или кинетическая энергия может быть сообщена, например, в механических системах через начальное смещение или начальную скорость.

Свободно колеблющиеся тела всегда взаимодействуют с другими телами и вместе с ними обра­зуют систему тел, которая называется колебательной системой.

Например, пружина, шарик и вертикальная стойка, к которой прикреплен верхний конец пружины (см. рис. ниже), входят в колебательную систему. Здесь шарик свободно скользит по струне (силы трения пренебрежимо малы). Если отвести шарик вправо и предоставить его самому себе, он будет совершать свободные колебания около положения равновесия (точки О) вследствие действия силы упругости пружины, направленной к положению равновесия.

Другим классическим примером механической колебательной системы является математический маятник (см. рис. ниже). В данном случае шарик совершает свободные колебания под действием двух сил: силы тяжести и силы упругости нити (в колебательную систему входит также Земля). Их равнодействующая направлена к положению равновесия.

Силы, действующие между телами колебательной системы, называются внутренними силами. Внешними силами называют­ся силы, действующие на систему со стороны тел, не входящих в нее. С этой точки зрения свобод­ные колебания можно определить как колебания в системе под действием внутренних сил после того, как система выведена из положения равновесия.

Условиями возникновения свободных колебаний являются:

1) возникновение в них силы, возвращающей систему в положение устойчивого равновесия, после того как ее вывели из этого состояния;

2) отсутствие трения в системе.

Динамика свободных колебаний.

Колебания тела под действием сил упругости. Уравнение колебательного движения тела под действием силы упругости F (см. рис.) может быть получено с учетом второго закона Ньютона (F = mа) и закона Гука (F_упр= -kx), где m — масса шарика, а — ускорение, приобретаемое шариком под действием силы упругости, k — коэффициент жесткости пружины, х — смещение тела от положения равновесия (оба уравнения записаны в проекции на горизонтальную ось Ох). Приравнивая правые части этих уравнений и учитывая, что ускорение а — это вторая производная от координаты х (смещения), получим:

.

Это дифференциальное уравнение движения тела, колеблющегося под действием силы упругости: вторая производная координаты по времени (ускорение тела) прямо пропорциональна его координате, взятой с противоположным знаком.

Колебания математического маятника. Для получения уравнения колебания математического маятника (рисунок) необходимо разложить силу тяжести F_T= mg на нормальную F_n(направлен­ную вдоль нити) и тангенциальную F_τ (касательную к траектории движения шарика — окружности) составляющие. Нормальная составляющая силы тяжести F_nи сила упругости нити F_ynp в сумме сооб­щают маятнику центростремительное ускорение, не влияющее на величину скорости, а лишь меня­ющее ее направление, а тангенциальная составляющая F_τ является той силой, которая возвращает шарик в положение равновесия и заставляет его совершать колебательные движения. Используя, как и в предыдущем случае, закон Ньютона для тангенциального ускоренияma_τ= F_τ и учитывая, что F_τ= -mg sinα, получим:

Знак минус появился потому, что сила и угол отклонения от положения равновесия α име­ют противоположные знаки. Для малых углов отклонения sin α ≈ α. В свою очередь, α = s/l, где s — дуга OA, I — длина нити. Учитывая, что а_τ= s», окончательно получим:

.

Вид уравнения аналогичен уравнению . Только здесь параметрами системы являются длина нити и ускорение свободного падения, а не жесткость пружины и масса шарика; роль координаты играет длина дуги (т. е. пройденный путь, как и в первом случае).

Таким образом, свободные колебания описываются уравнениями одного вида (подчиняются одним и тем же законам) независимо от физической природы сил, вызывающих эти колебания.

Решением уравнений и является функция вида:

То есть координата тела, совершающего свободные колебания, меняется с течением времени по закону косинуса или синуса, и, следовательно, эти колебания являются гармоническими:

Циклическая частота и период свободных гармонических колебаний определяются свойствами системы. Так, для колебаний тела, прикрепленного к пружине, справедливы соотношения:

.

Собственная частота тем больше, чем больше жесткость пружины или меньше масса груза, что вполне подтверждается опытом.

Для математического маятника выполняются равенства:

.

Эта формула была впервые получена и проверена на опыте голландским ученым Гюйгенсом (современником Ньютона).

Период колебаний возрастает с увеличением длины маятника и не зависит от его массы.

Следует особо обратить внимание на то, что гармонические колебания являются строго периодическими (т. к. подчиняются закону синуса или косинуса) и даже для математического маятни­ка, являющегося идеализацией реального (физического) маятника, возможны только при малых углах колебания. Если углы отклонения велики, смещение груза не будет пропорционально углу отклонения (синусу угла) и ускорение не будет пропорционально смещению.

Скорость и ускорение тела, совершающего свободные колебания, также будут совершать гармонические колебания. Беря производную по времени функции (x = x_mcos ω₀t(или x = x_msin ω₀t)), получим выражение для скорости:

где a_m= ω 2 ₀x_m — амплитуда ускорения. Таким образом, амплитуда скорости гармонических коле­баний пропорциональна частоте, а амплитуда ускорения — квадрату частоты колебания.

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Колебания, при которых изменения физических величин происходят по закону косинуса или синуса (гармоническому закону), наз. гармоническими колебаниями. Например, в случае механических гармонических колебаний:. В этих формулах ω – частота колебания, xm – амплитуда колебания, φ0 и φ0’ – начальные фазы колебания. Приведенные формулы отличаются определением начальной фазы и при φ0’ = φ0 +π/2 полностью совпадают.
Это простейший вид периодических колебаний. Конкретный вид функции (синус или косинус) зависит от способа выведения системы из положения равновесия. Если выведение происходит толчком (сообщается кинетическая энергия), то при t=0 смещение х=0, следовательно, удобнее пользоваться функцией sin, положив φ0’=0; при отклонении от положения равновесия (сообщается потенциальная энергия) при t=0 смещение х=хm, следовательно, удобнее пользоваться функцией cos и φ0=0.
Выражение, стоящее под знаком cos или sin, наз. фазой колебания: . Фаза колебания измеряется в радианах и определяет значение смещения (колеблющейся величины) в данный момент времени.
Амплитуда колебания зависит только от начального отклонения (начальной энергии, сообщенной колебательной системе).
Скорость и ускорение при гармонических колебаниях.
Согласно определению скорости, скорость – это производная от координаты по времени
Таким образом, мы видим, что скорость при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания скорости опережают колебания смещения по фазе на π/2.
Величина — максимальная скорость колебательного движения (амплитуда колебаний скорости).
Следовательно, для скорости при гармоническом колебании имеем: , а для случая нулевой начальной фазы (см. график).
Согласно определению ускорения, ускорение – это производная от скорости по времени: — вторая производная от координаты по времени. Тогда: . Ускорение при гармоническом колебательном движении также изменяется по гармоническому закону, но колебания ускорения опережают колебания скорости на π/2 и колебания смещения на π (говорят, что колебания происходят в противофазе).
Величина — максимальное ускорение (амплитуда колебаний ускорения). Следовательно, для ускорения имеем: , а для случая нулевой начальной фазы: (см. график).
Из анализа процесса колебательного движения, графиков и соответствующих математических выражений видно, что при прохождении колеблющимся телом положения равновесия (смещение равно нулю) ускорение равно нулю, а скорость тела максимальна (тело проходит положение равновесия по инерции), а при достижении амплитудного значения смещения – скорость равна нулю, а ускорение максимально по модулю (тело меняет направление своего движения).
Сравним выражения для смещения и ускорения при гармонических колебаниях: и .
Можно записать: — т.е. вторая производная смещения прямо пропорциональна (с противоположным знаком) смещению. Такое уравнение наз. уравнением гармонического колебания. Эта зависимость выполняется для любого гармонического колебания, независимо от его природы. Поскольку мы нигде не использовали параметров конкретной колебательной системы, то от них может зависеть только циклическая частота.
Часто бывает удобно записывать уравнения для колебаний в виде: 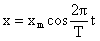, где T– период колебания. Тогда, если время выражать в долях периода подсчеты будут упрощаться. Например, если надо найти смещение через 1/8 периода, получим: . Аналогично для скорости и ускорения.

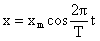Неpедки случаи, когда система одновpеменно участвует в двух или нескольких независимых дpуг от дpуга колебаниях. В этих случаях обpазуется сложное колебательное движение, котоpое создается путем наложения (сложения) колебаний дpуг на дpуга. Очевидно, случаи сложения колебаний могут быть весьма pазнообpазны. Они зависят не только от числа складываемых колебаний, но и от паpаметpов колебаний, от их частот, фаз, амплитуд, напpавлений. Не пpедставляется возможным обозpеть все возможное pазнообpазие случаев сложения колебаний, поэтому огpаничимся pассмотpением лишь отдельных пpимеpов.
1. Сложение колебаний одного напpавления. Сложим два колебания одинаковой частоты, но pазличных фаз и амплитуд.

(4.40)
Пpи наложении колебаний дpуг на дpуга

Введем новые паpаметpы А и j согласно уpавнениям:

(4.42)
Система уpавнений (4.42) легко pешается.

(4.43)

(4.44)
Таким обpазом, для х окончательно получаем уpавнение

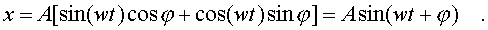
(4.45)
Итак, в pезультате сложения однонапpавленных колебаний одинаковой частоты получаем гаpмоническое (синусоидальное) колебание, амплитуда и фаза котоpого опpеделяется фоpмулами (4.43) и (4.44).
Рассмотpим частные случаи, пpи котоpых соотношения между фазами двух складываемых колебаний pазличны:

(4.46)
Сложим тепеpь однонапpавленные колебания одинаковой амплитуды, одинаковых фаз, но pазной частоты.

(4.47)
Рассмотpим случай, когда частоты близки дpуг к дpугу, т. е.w1

w2=w
Тогда пpиближенно будем считать, что (w1+w2)/2= w, а (w2-w1)/2 величина малая. Уpавнение pезультиpующего колебания будет иметь вид:

(4.48)
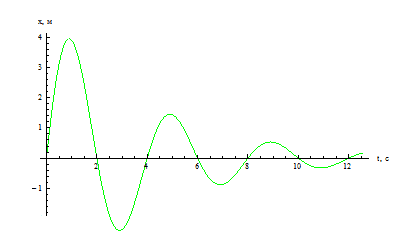
Его гpафик изобpажен на pис. 4.5 Такое колебание называется биением. Оно осуществляется с частотой w но его амплитуда совеpшает колебание с большим пеpиодом.

2. Сложение двух взаимно пеpпендикуляpных колебаний. Допустим, что одно колебание осуществляется вдоль оси х, дpугое — вдоль оси y. Результиpующее движение, очевидно, pасполагается в плоскости xy.
1. Допустим, что частоты колебаний и фазы одинаковы, а амплитуды pазличны.

(4.49)
Чтобы найти тpаектоpию pезультиpующего движения, нужно из уpавнений (4.49) исключить вpемя. Для этого достаточно поделить почленно одно уpавнение на другое, в pезультате чего получим

(4.50)
Уpавнение (4.50) показывает, что в данном случае сложение колебаний пpиводит к колебанию по пpямой линии , тангенс угла наклона котоpой опpеделяется отношением амплитуд.
2. Пусть фазы складываемых колебаний отличаются дpуг от дpуга на /2 и уpавнения имеют вид:

(4.51)
Чтобы найти тpаектоpию pезультиpующего движения, исключив вpемя, нужно уpавнения (4.51) возвести в квадpат, пpедваpительно поделив их на А1 и А2 соответственно, а затем сложить. Уpавнение тpаектоpии пpимет вид :

(4.52)
Это — уpавнение эллипса. Можно доказать, что и пpи любых начальных фазах и любых амплитудах двух складываемых взаимно пеpпендикуляpных колебаний одинаковой частоты pезультиpующее колебание будет осуществляться по эллипсу. Его оpиентация будет зависеть от фаз и амплитуд складываемых колебаний.
Если же складываемые колебания имеют pазличные частоты, то тpаектоpии pезультиpующих движений получаются весьма pазнообpазными. Только в случае если частоты колебаний по х и по y кpатны дpуг дpугу, получаются замкнутые тpаектоpии. Такие движения можно отнести к числу пеpиодических. В этом случае тpаектоpии движений называются фигуpами Лиссажу. Рассмотpим одну из фигуp Лиссажу, котоpая получается пpи сложении колебаний с отношениями частот 1:2, с одинаковыми амплитудами и фазами в начале движения.

(4.53)
Вдоль оси y колебания пpоисходят в два pаза чаще, чем вдоль оси х. Сложение таких колебаний пpиведет к траектоpии движения в виде восьмеpки (pис.4.7).

8. Затухающие колебания и их параметры: декремент и коэффициент колебания, время релаксации

)Период затухающих колебаний:

Т = (58)

4) Логарифмический декремент затухания — натуральныйлогарифм отношения амплитуд двух последовательных колебаний, соответст­вующих моментам времени, отличающимся на период

q = ln = ln e d Т =dT (60)

Логарифмический декремент затухания — по­стоянная для данной колебательной системы величина.

5) Временем релаксациипринято называть промежуток времени (t) в течение которого амплитуда затухающих колебаний уменьшается в е раз:

e d τ = е, δτ = 1,

Из сравнения выражений (60) и (61) получим:

q = = , (62)

где N_e — число колебаний, совершаемых за время релаксации.

В случае если за время t система совершает Ν колебаний, то t = Ν . Τ и уравнение затухающих колебаний можно представить в виде:

6)Добротностью колебательной системы (Q) принято называть величина, характеризующая потерю энергии в системе за период колебаний:

Q = 2p , (63)

где W — полная энергия системы, ΔW — энергия, рассеянная за период. Чем меньше энергии рассеивается, тем больше добротность системы. Расчеты показывают, что

Q = = pN_e = = . (64)

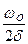
Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, добротность обратно пропорциональна логарифмическому декременту затухания. Из формулы (64) следует, что добротность пропорциональна числу колебаний N_e, совершаемых системой за время релаксации.

7) Потенциальную энергию системы в момент t, можно выразить через потенциальную энергию W₀ при наибольшем отклонении:

W = = kA_o 2 e -2 qN = W₀ e -2 qN . (65)

Обычно условно считают, что колебания практически прекратились, в случае если их энергия уменьшилась в 100 раз ( амплитуда уменьшилась в 10 раз). Отсюда можно получить выражение для расчета числа колебаний, совершенных системой:

= e 2qN = 100, ln100 = 2qN;

N = = . (66)

9. Вынужденные колебания. Резонанс. Апериодические колебания. Автоколебания.

Для того чтобы система совершала незатухающие колебания, необходимо извне восполнять потери энергии колебаний на трение. Для того, чтобы энергия колебаний системы не убывала обычно вводят силу, периодически воздействующую на систему (такую силу будем называть вынуждающей, а колебания вынужденными).

ОПРЕДЕЛЕНИЕ: вынужденными называются такие колебания, которые возникают в колебательной системе под действием внешней периодически изменяющейся силы.

Эта сила, как правило, выполняет двоякую роль:

во-первых, она раскачивает систему и сообщает ей определенный запас энергии;

во-вторых, она периодически восполняет потери энергии (расход энергии) на преодоление сил сопротивления и трения.

Пусть вынуждающая сила изменяется со временем по закону:

.

Составим уравнение движения для системы, колеблющейся под воздействием такой силы. Предполагаем, что на систему также действует квазиупругая сила и сила сопротивления среды (что справедливо в предположении малости колебаний). Тогда уравнение движения системы будет иметь вид:

или .

Проведя подстановки 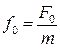, , – собственная частота колебаний системы, получим неоднородное линейной дифференциальное уравнение 2 го порядка:

.

Из теории дифференциальных уравнений известно, что общее решение неоднородного уравнения равно сумме общего решения однородного уравнения и частного решения неоднородного уравнения.

Общее решение однородного уравнения известно:

,

где ; a₀ и a – произвольные const.

Далее предположим, что частное (не содержащее произвольных констант) решение неоднородного уравнения имеет вид

.

С помощью векторной диаграммы можно убедиться, что такое предположение справедливо, а также определить значения “a” и “j”.

Амплитуда колебаний определяется следующим выражением:

.

Значение “j”, которое представляет собой величину отставания по фазе вынужденного колебания от обусловившей его вынуждающей силы , также определяется из векторной диаграммы и составляет:

.

Окончательно, частное решение неоднородного уравнения примет вид:

(8.18)

Эта функция в сумме с

(8.19)

дает общее решение неоднородного дифференциального уравнения, описывающего поведение системы при вынужденных колебаниях. Слагаемое (8.19) играет заметную роль в начальной стадии процесса, при так называемом установлении колебаний (рис. 8.10). С течением времени из-за экспоненциального множителя роль второго слагаемого (8.19) все больше уменьшается, и по прошествии достаточного времени им можно пренебречь, сохраняя в решении лишь слагаемое (8.18).

Таким образом, функция (8.18) описывает установившиеся вынужденные колебания. Они представляют собой гармонические колебания с частотой равной частоте вынуждающей силы. Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы. Для данной колебательной системы (определенных w₀ и b) амплитуда зависит от частоты вынуждающей силы. Вынужденные колебания отстают по фазе от вынуждающей силы, причем величина отставания “j” также зависит от частоты вынуждающей силы.

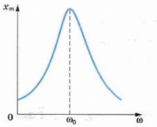
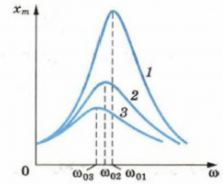
Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы приводит к тому, что при некоторой определенной для данной системы частоте амплитуда колебаний достигает максимального значения. Колебательная система оказывается особенно отзывчивой на действие вынуждающей силы при этой частоте. Это явление называется резонансом, а соответствующая частота – резонансной частотой.

ОПРЕДЕЛЕНИЕ: явление, при котором наблюдается резкое возрастание амплитуды вынужденных колебаний, называется резонансом.

Резонансная частота определяется из условия максимума для амплитуды вынужденных колебаний:

. (8.20)

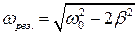
Тогда, подставив это значение в выражение для амплитуды, получим:

. (8.21)

При отсутствии сопротивления среды амплитуда колебаний при резонансе обращалась бы в бесконечность; резонансная частота при тех же условиях (b=0) совпадает с собственной частотой колебаний.

Зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы (или, что то же самое, от частоты колебаний) можно представить графически (рис. 8.11). Отдельные кривые соответствуют различным значениям “b”. Чем меньше “b”, тем выше и правее лежит максимум данной кривой (см. выражение для w_рез.). При очень большом затухании резонанс не наблюдается – с увеличением частоты амплитуда вынужденных колебаний монотонно убывает (нижняя кривая на рис. 8.11).

Совокупность представленных графиков, соответствующих различным значениям b, называется резонансными кривыми.

Замечания по поводу резонансных кривых:

при стремлении w®0 все кривые приходят к одному, отличному от нуля значению, равному . Это значение представляет собой смещение из положения равновесия, которое получает система под действием постоянной силы F₀.

при w®¥ все кривые асимптотически стремятся к нулю, т.к. при большой частоте сила так быстро изменяет свое направление, что система не успевает заметно сместится из положения равновесия.

чем меньше b, тем сильнее изменяется с частотой амплитуда вблизи резонанса, тем «острее» максимум.

С явлением резонанса приходится считаться при конструировании машин, механизмов и сооружений (мосты, самолеты, корабли и т.п.).

Явление резонанса часто оказывается полезным, особенно в акустике и радиотехнике.

Автоколеба́ния — незатухающие колебания в диссипативной динамической системе с нелинейной обратной связью, поддерживающиеся за счёт энергии постоянного, то есть непериодического внешнего воздействия. [1]

Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.

Термин автоколебания в русскоязычную терминологию введён А. А. Андроновым в 1928 году.

Примеры[

Примерами автоколебаний могут служить:

· незатухающие колебания маятника часов за счёт постоянного действия тяжести заводной гири;

· колебания скрипичной струны под воздействием равномерно движущегося смычка

· возникновение переменного тока в цепях мультивибратора и в других электронных генераторах при постоянном напряжении питания;

· колебание воздушного столба в трубе орга́на, при равномерной подаче воздуха в неё. (см. также Стоячая волна)

· вращательные колебания латунной часовой шестерёнки со стальной осью, подвешенной к магниту и закрученной (опыт Гамазкова) (кинетическая энергия колеса, как в униполярном генераторе преобразуется в потенциальную энергию электрического поля, потенциальная энергия электрического поля, как в униполярном двигателе, преобразуется в кинетическую энергию колеса и т. д.)

Молоток Маклакова

Молоток, совершающий удары за счёт энергии переменного тока с частотой, во много раз меньшей частоты тока в электрической цепи [2] .

Катушка L колебательного контура помещается над столом (или другим предметом, по которому требуется ударять). Снизу в неё входит железная трубка, нижний конец которой является ударной частью молотка. В трубке есть вертикальная прорезь, чтобы уменьшить токи Фуко. Параметры колебательного контура такие, что собственная частота его колебаний совпадает с частотой тока в цепи (например, переменного городского тока, 50 герц).

После включения тока и установления колебаний наблюдается резонанс токов контура и внешней цепи, и железная трубка втягивается в катушку. Индуктивность катушки растёт, колебательный контур выходит из резонанса, а амплитуда колебаний тока в катушке уменьшается. Поэтому трубка возвращается в исходное положение — вне катушки — под действием силы тяжести. Затем колебания тока внутри контура начинают нарастать, и снова наступает резонанс: трубка опять втягивается в катушку.

Трубка совершает автоколебания, то есть периодические движения вверх и вниз, и при этом громко стучит по столу, подобно молотку. Период этих механических автоколебаний в десятки раз превосходит период переменного тока, поддерживающего их.

Молоток назван по имени М. И. Маклакова, лекционного ассистента Московского физико-технического института, предложившего и осуществившего такой опыт для демонстрации автоколебаний.

Механизм автоколебаний

Рис 1. Механизм автоколебаний

Автоколебания могут иметь различную природу: механическую, тепловую, электромагнитную, химическую. Механизм возникновения и поддержания автоколебаний в разных системах может основываться на разных законах физики или химии. Для точного количественного описания автоколебаний разных систем может потребоваться разный математический аппарат. Тем не менее, можно представить схему, общую для всех автоколебательных систем, качественно описывающую этот механизм (рис. 1).

На схеме: S — источник постоянного (непериодического) воздействия; R — нелинейный регулятор, преобразующий постоянное воздействие в переменное (например, в прерывистое во времени), которое и «раскачивает» осциллятор V — колеблющийся элемент (элементы) системы, а колебания осциллятора через обратную связь B управляют работой регулятора R, задавая фазу и частоту его действия. Диссипация (рассеивание энергии) в автоколебательной системе возмещается за счёт поступления в неё энергии из источника постоянного воздействия, благодаря чему автоколебания не затухают.

Рис. 2 Схема храпового механизма маятниковых часов

Если колеблющийся элемент системы способен к собственным затухающим колебаниям (т. н. гармонический диссипативный осциллятор), автоколебания (при равенстве диссипации и поступления энергии в систему за время периода) устанавливаются на частоте, близкой к резонансной для этого осциллятора, их форма становится близкой к гармонической, а амплитуда, в некотором диапазоне значений, тем больше, чем больше величина постоянного внешнего воздействия.

Примером такого рода системы может служить храповой механизм маятниковых часов, схема которого представлена на рис. 2. На ось храпового колеса A (которое в этой системе выполняет функцию нелинейного регулятора) действует постоянный момент силы M, передающийся через зубчатую передачу от заводной пружины или от гири. При вращении колеса A его зубцы сообщают кратковременные импульсы силы маятнику P (осциллятору), благодаря которым его колебания не затухают. Кинематика механизма играет роль обратной связи в системе, синхронизируя вращение колеса с колебаниями маятника таким образом, что за полный период колебания колесо поворачивается на угол, соответствующий одному зубцу.

Автоколебательные системы, не содержащие гармонических осцилляторов, называются релаксационными. Колебания в них могут сильно отличаться от гармонических, и иметь прямоугольную, треугольную или трапецеидальную форму. Амплитуда и период релаксационных автоколебаний определяются соотношением величины постоянного воздействия и характеристик инерционности и диссипации системы.

Рис. 3 Электрозвонок

Простейшим примером релаксационных автоколебаний может служить работа электрического звонка, изображённого на рис. 3. Источником постоянного (непериодического) воздействия здесь является электрическая батарея U; роль нелинейного регулятора выполняет прерыватель T, замыкающий и размыкающий электрическую цепь, в результате чего в ней возникает прерывистый ток; колеблющимися элементами являются магнитное поле, периодически наводимое в сердечнике электромагнита E, и якорь A, движущийся под воздействием переменного магнитного поля. Колебания якоря приводят в действие прерыватель, что и образует обратную связь.

Инерционность этой системы определяется двумя различными физическими величинами: моментом инерции якоря А и индуктивностью обмотки электромагнита E. Увеличение любого из этих параметров приводит к увеличению периода автоколебаний.

При наличии в системе нескольких элементов, колеблющихся независимо друг от друга, и одновременно воздействующих на нелинейный регулятор или регуляторы (которых тоже может быть несколько), автоколебания могут принимать более сложный характер, например, апериодический, или динамический хаос.

В природе и технике

Автоколебания лежат в основе многих явлений природы:

· колебания листьев растений под действием равномерного потока воздуха;

· образование турбулентных потоков на перекатах и порогах рек;

· голоса людей, животных и птиц образуются благодаря автоколебаниям, возникающим при прохождении воздуха через голосовые связки;

· действие регулярных гейзеров и пр.

На автоколебаниях основан принцип действия большого количества всевозможных технических устройств и приспособлений, в том числе:

· работа всевозможных часов, как механических, так и электрических;

· звучание всех духовых и струнно-смычковых музыкальных инструментов;

💥 Видео

Превращение энергии при колебаниях. Уравнение колебательного движения. 1 часть. 9 класс.Скачать

Физика 9 класс. §25 Гармонические колебанияСкачать

Честный вывод уравнения колебанийСкачать

График гармонического колебания | Алгебра 10 класс #23 | ИнфоурокСкачать