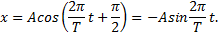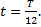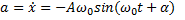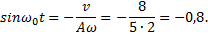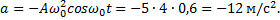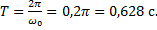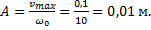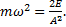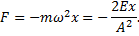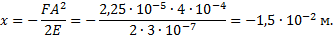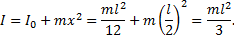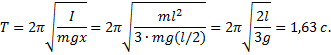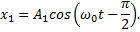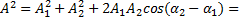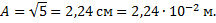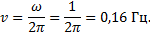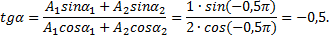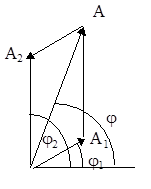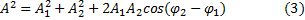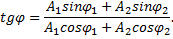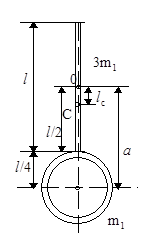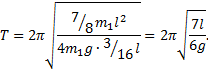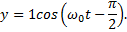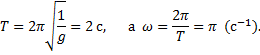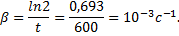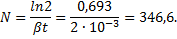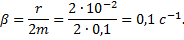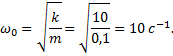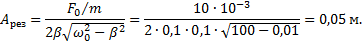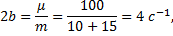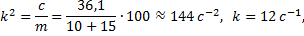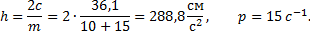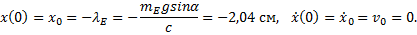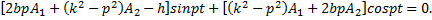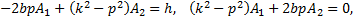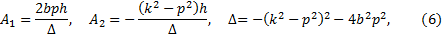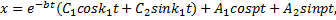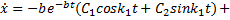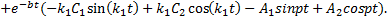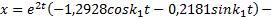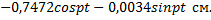КОЛЕБАНИЯ И ВОЛНЫ
Через какое время от начала движения точка, которая выполняет гармонические колебания, сместится от положения равновесия на половину амплитуды? Период колебаний Т = 24 с, начальная фаза φ0 = 0.
Дано:
Решение:
Уравнение колебаний запишем в виде

Циклическую частоту найдем, зная период колебаний Т
Из формулы (1) найдем время t
Ответ:
Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать

Через какое минимальное время t, считая от начала колебаний, смещение колеблющейся материальной точки составит половину амплитуды? Период колебаний T = 24 с.






Чтобы получить решение , напишите мне в WhatsApp , оплатите, и я Вам вышлю файлы.
Кстати, если эта работа не по вашей теме или не по вашим данным , не расстраивайтесь, напишите мне в WhatsApp и закажите у меня новую работу , я смогу выполнить её в срок 1-3 дня!
Описание и исходные данные задания, 50% решения + фотография:
№1-1 (по закону синуса) 110. Через какое минимальное время t, считая от начала колебаний, смещение колеблющейся материальной точки составит половину амплитуды? Период колебаний T = 24 с. Найти среднюю скорость v точки за это время. Амплитуда колебаний A = 0,1 м.
Уравнение гармонических колебаний материальной точки при условии, что положение равновесия точка проходит в начальный момент времени, имеет вид:
| Если вам нужно решить физику, тогда нажмите ➔ заказать контрольную работу по физике. |
| Похожие готовые решения: |
- Через сколько времени от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний равен 24 с, начальная фаза равна нулю.
- Точка совершает гармонические колебания с периодом T = 6 с и начальной фазой, равной нулю. Определите, за какое время, считая от начала движения, точка сместится от положения равновесия на половину амплитуды.
- Груз массой m = 200 г, подвешенный на пружине, удлиняет её на ∆l = 8 см. Определить отношение её кинетической и потенциальной энергии и фазу колебания в момент времени t = 1 с, отсчитывая от момента прохождения маятником положения равновесия. Предложить альтернативным способом вычисление энергии.
- Частица совершает гармонические колебания вдоль оси ОХ около положения равновесия. Циклическая частота колебаний частицы w = 4 рад/с. В какой момент времени t после прохождения положения равновесия частица будет иметь координату x = 25 см и скорость v = 100 см/с?
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать

Примеры решения задач
Пример 1. Колебания материальной точки происходят относительно положения равновесия по закону х=А∙sinωt с периодом T=12 с. Определить, за какой наименьший промежуток времени t1 точка удалится от положения равновесия на расстояние, равное половине амплитуды x=A/2. За какой промежуток времени t2 она пройдет оставшуюся часть пути до максимального отклонения.
Решение. В момент времени t1 cмещение равно А/2: А/2=А∙sinωt1, sinωt1=1/2, т.е. ωt1=π/6, или (2π/Т)t1=π/6.
Расстояние от точки равновесия до точки максимального отклонения материальная точка проходит за t=T/4. Следовательно, t2=T/4- T/12= 2 c.
Пример 2.За какую часть периода точка, совершающая гармонические колебания по закону косинуса, сместится на половину амплитуды, если в начальный момент она находилась в положении равновесия?
Решение.Колебания точки описываются уравнением x=Acos(ω0t+α). Поскольку при t = 0 смещение х = 0, то начальная фаза φ должна равняться π/2, т.е. уравнение имеет вид:
По условию смещение x=A/2, следовательно, 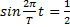
Отсюда 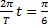
Пример 3.Точка совершает колебания по закону x=5cosω0t (м), где ω0= 2 с –1 . Определить ускорение точки в момент времени, когда ее скорость равна 8 м/с.
Решение.Зависимости скорости и ускорения колеблющейся точки от времени задаются уравнениями
Следовательно, 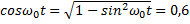
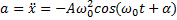
Пример 4.Максимальная скорость точки, совершающей гармонические колебания, равна 10 см/с, максимальное ускорение равно 100 см/с 2 . Найти циклическую частоту колебаний, их период и амплитуду.
Решение.Из формул
a=-A 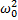
Период
Амплитуда
Пример 5.Амплитуда гармонических колебаний материальной точки А = 0,02 м, полная энергия колебаний W=3∙10 –7 Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила F= 2,25∙10 –5 Н?
Решение.Из 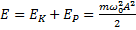
Тогда, используя выражение F=-kx, получим
Пример 6.В качестве физического маятника используется стержень, подвешенный за один из его концов. Чему равен период колебаний при длине стержня 1 м?
Решение.Для того, чтобы воспользоваться формулой 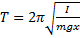
Тогда, учитывая, что x=l/2,
Пример 7.Два одинаково направленных гармонических колебания заданы уравнениями x1=A1∙sinω0t и x2=A2∙cosω0t, где А1 = 1 см; А2 = 2 см; ω0 = 1 с –1 . Определить амплитуду результирующего колебания А, его частоту v и начальную фазу α. Найти уравнение этого движения.
Решение.Преобразуем первое уравнение, заданное в условии задачи, к виду x=A∙cos(ω0t+α) и получим
Тогда по формуле 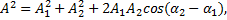
=1+4+2∙2∙cos0,5π=5 см 2 .
Частота результирующего колебания равна частоте складывающихся колебаний
Начальную фазу находим по формуле:
Начальная фаза α=arctg(-0,5)=-26,6°=-0,46 рад.
Уравнение результирующего колебания имеет вид x=2,24∙10 -2 cos(t-0,46) м.
Пример 8.Складываются два колебания одинакового направления (рис.23), выражаемых уравнениями x1=A1cosω(t+τ1) и x2=A2cosω(t+τ2), где А1=1 см; А2=2 см; τ1=1/6 с; τ2=1/2 с; ω=π рад/с. Определить начальные фазы φ1 и φ2 составляющих колебаний; найти амплитуду А и начальную фазу φ результирующего колебания.
Рис.23
Решение. Уравнение гармонического колебания имеет вид:
Преобразуем уравнения, заданные в условии задачи, к такому же виду:
Из сравнения выражений (2) с (1) находим начальные фазы первого и второго колебаний: φ1=ωτ1=π/6 рад и φ2= ωτ2=π/2 рад.
Для определения амплитуды А результирующего колебания удобно воспользоваться векторной диаграммой, представленной на рис.23.
Согласно теореме косинусов, получим:
Подставим значения А1, А2 и φ2-φ1 в (3), извлечем корень и получим: А=2,65 см.
Тангенс начальной фазы результирующего колебания определим непосредственно из рисунка 41.1:
Тогда φ=arctg(5/ 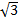
Так как циклические частоты складываемых колебаний одинаковы, то результирующее колебание будет иметь ту же частоту ω.
Это позволяет написать уравнение результирующего колебания в виде х=А∙cos(ωt+φ),
где А=2,65 см, ω=π рад/с, φ=0,394π рад.
Пример 9. Шарик массой m=10 -2 кг=10 г совершает гармонические колебания с амплитудой А=0,2 м и периодом Т=4 с. В начальный момент времени t=0: х=А. Найти кинетическую и потенциальную энергию в момент времени t= 1 с.
Решение: Запишем уравнение гармонических колебаний
Т.к. при t=0 х=А, то можно определить начальную фазу Асоs(ω∙0+φ0)=A, соsφ0=1, φ0=0.
Таким образом, х=0,2cos[(2π/4)t]= 0,2cos[(π/2)t] (м).
Кинетическая энергия шарика определяется по формуле: Ек=mv 2 /2, где v=dx/dt=-Aω∙sinωt.
Ек=[mA 2 ω 2 ∙sin 2 ωt]/2=5∙10 -3 Дж.
Потенциальная энергия шарика равна:
Еп=kx 2 /2=[kА 2 cos 2 ωt]/2=[kА 2 cos 2 (π/2)]/2,
Пример 10. Физический маятник представляет собой стержень длиной l=1 м и массой mc=3m1 с прикрепленным к одному из его концов обручем диаметром d=l/2 и массой mо=m1. Горизонтальная ось ОZ проходит через середину стержня перпендикулярно ему (рис. 24). Определить период колебаний такого маятника T — ?.
Рис.24
Решение. Период колебаний физического маятника определяется по формуле
где J — момент инерции маятника относительно оси колебаний, m — его масса, lc — расстояние от центра масс маятника до оси колебаний. Момент инерции маятника равен сумме моментов инерции стержня J1 и обруча J2:
Момент инерции стержня относительно оси, перпендикулярной стержню и проходящей через его центр масс, определяется по формуле J1=mcl 2 /12, т.е. J1=m1l 2 /4.
Момент инерции обруча найдем, воспользовавшись теоремой Штейнера J=Jo+ma 2 . Применив эту формулу к обручу, получим
Подставив выражения J1 и J2 в формулу (2), найдем момент инерции маятника относительно оси вращения:
Расстояние lc от оси маятника до его центра масс равно
Подставив в формулу (1) выражения J, Jc и массы маятника (m=3m1+m1=4m1), найдем период его колебаний:
После вычисления по этой формуле получим Т=2,17 с.
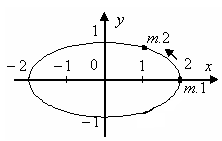
Пример 11. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях (рис.25), выражаемых уравнениями x=2cosω0t (см) и y=sinω0t (см). Найти уравнение траектории точки и построить ее, указав направление движения, если ω0=π/3 (с –1 ).
Рис.25
Решение.Преобразуем второе уравнение к виду y=Аcos(ω0t+α) и получим:
Как видно, разность фаз складывающихся колебаний α= -π/2 и это соответствует частному случаю, когда уравнение траектории имеет вид: 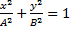
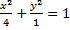
Для того, чтобы указать направление движения точки, необходимо проследить, как меняется ее положение с течением времени. Для этого найдем координаты точки для двух ближайших моментов времени. Период результирующих колебаний 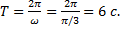
Следовательно, точка 1 имеет координаты (2; 0), а точка 2 – (1; 0,86). Это означает, что движение происходит против часовой стрелке.
Пример 12.Амплитуда колебаний математического маятника длиной 1 м за время 10 мин уменьшилась в 2 раза. Определить коэффициент затухания, логарифмический декремент затухания колебаний и количество колебаний, совершенных за это время. Записать уравнение колебаний, если в начальный момент маятник был отведен из положения равновесия на 5 см и отпущен.
Решение.Период и частоту колебаний математического маятника найдем из выражения:
Запишем отношение амплитуд (начальной A0=5 см и через время t = 10 мин = 600 с):
следовательно, βt=ln2, отсюда
Количество колебаний N, совершенных за время t , найдем из того, что t=NT, а, значит, βNT=ln2, и тогда
Логарифмический декремент затухания определим по:
Выбор гармонической функции для написания уравнения колебаний проведем на основании того, что в начальный момент смещение точки от положения равновесия равно амплитуде, а этому условию удовлетворяет функция косинус. Тогда уравнение данных затухающих колебаний имеет вид: x=5∙10 -2 e -0,001 t cosπt (м).
Пример 13.Пружинный маятник, (жесткость пружины которого равна k = 10 Н/м, а масса груза m = 100 г) совершает вынужденные колебания в вязкой среде с коэффициентом сопротивления r = 0,02 кг/с. Определить коэффициент затухания β и резонансную амплитуду Арез, если амплитудное значение вынуждающей силы F0 = 10 мН.
Решение.Коэффициент затухания:
Тогда резонансная частота:
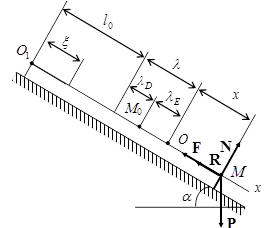
Пример 14.Тело D массы mD = 10 кг расположено на гладкой плоскости, наклоненной под углом 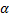
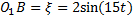
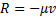

Рис.26
Решение. Направим оси Ox и 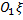
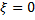
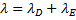
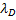
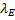
Рис.27
Изобразим грузы в промежуточном положении, отстоящем от начала координат на величину x (точка M). Если бы верхний конец пружины был неподвижен, то в этом положении пружина была бы растянута на величину ( 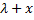
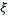
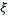
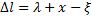
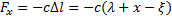
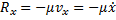

где 
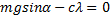
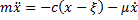
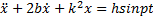
Начальные условия для уравнения (1) определяются соотношениями
Как известно, решение линейного дифференциального уравнения (1) складывается из общего решения 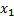
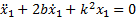
и частного решения x2 неоднородного уравнения (1)
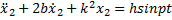
Общее решение однородного уравнения (2) имеет вид
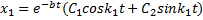
Частное решение неоднородного уравнения (3) будем искать в виде
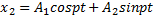
Определив производные 
Чтобы полученное равенство выполнялось в любой момент времени, необходимо равенство нулю выражений в квадратных скобках. Таким образом, для определения коэффициентов A1 и A2 имеем систему из двух линейных уравнений
решение которой записывается так
или после подстановки численных данных
|
Следовательно, решение уравнения (1) принимает вид
причем скорость точки равна
Постоянные интегрирования C1 и C2 определим из начальных условий: С1 = –1.2928 см, С2 = –0.2181 см. В результате уравнение движения груза имеет вид
Вопросы для самопроверки
— Под действием какой силы совершаются свободные колебания материальной точки?
— Какой вид имеет дифференциальное уравнение свободных колебаний материальной точки?
— От каких факторов зависят частота, период, амплитуда и начальная фаза свободных колебаний материальной точки?
— Каков вид графиков свободных и затухающих колебаний, а также апериодического движения материальной точки?
— Какой вид имеет дифференциальное уравнение вынужденных колебаний материальной точки и каково его общее решение?
— Из каких составляющих движений складывается движение материальной точки, находящейся под действием восстанавливающей и возмущающей сил?
— Каковы частота и период вынужденных колебаний материальной точки?
— Какие вынужденные колебания называются колебаниями малой частоты и какие – колебаниями большой частоты? Чем характеризуется тот и другой вид колебаний?
— От каких факторов зависит амплитуда вынужденных колебаний точки?
— Что называют коэффициентом динамичности и каков график его зависимости от отношения p/k?
— При каком условии возникает явление биений? Каков график биений?
— При каких условиях возникает резонанс и каковы уравнения и график вынужденных колебаний материальной точки при резонансе?
— Как влияет сопротивление, пропорциональное скорости, на амплитуду, фазу, частоту и период вынужденных колебаний?
— Как определить максимальное значение амплитуды вынужденных колебаний при данном значении коэффициента затухания n?
— При каком значении коэффициента затухания максимум амплитуды вынужденных колебаний не существует?
— Какова зависимость сдвига фазы колебаний 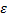
🎬 Видео
Уравнения и графики механических гармонических колебаний. 11 класс.Скачать

Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать

Выполнялка 53.Гармонические колебания.Скачать

Урок 327. Гармонические колебанияСкачать

МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать

Физика 9 класс. §25 Гармонические колебанияСкачать

5.4 Уравнение гармонических колебанийСкачать

Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать

Урок 330. Скорость и ускорение при гармонических колебанияхСкачать

10 класс, 19 урок, График гармонического колебанияСкачать

Урок 335. Анализ графика гармонических колебанийСкачать

Величины, характеризующие колебательное движение | Физика 9 класс #24 | ИнфоурокСкачать

Ацюковский: Уравнения Шрёдингера - уравнение колебаний материальной точкиСкачать

Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать

Гармонические колебания материальной точкиСкачать

Урок 329. Задачи на гармонические колебания - 1Скачать

КОЛЕБАНИЯ физика 9 класс решение задачСкачать

Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать