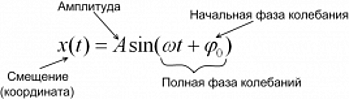уравнение гармонических колебаний
Точка совершает простые гармонические колебания, уравнение которых x = Asinωt, где А = 5 см, ω = 2 с. В момент времени, когда точка обладала потенциальной энергией П = 0,1 мДж, на нее действовала возвращающая сила F = 5 мН. Найти этот момент времени t.
Написать уравнение гармонического колебания, если амплитуда его 10 см, максимальная скорость 50 см/с, начальная фаза 15°. Определить период колебания и смещение колеблющейся точки через 0,2 с от начала колебания.
Запишите уравнение гармонического колебания материальной точки, если его амплитуда А = 10 см, максимальная скорость колеблющейся точки vmax = 20 см/с, начальная фаза 15°.
Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения двух одинаково направленных колебаний, заданных уравнениями x1 = 4sinπt см и x2 = 3sin(πt + π/2) см. Найти уравнение результирующего колебания. Представить решение в виде векторной диаграммы.
Напишите уравнение гармонического колебания точки, если его амплитуда A = 15 см, максимальная скорость колеблющейся точки vmax = 30 см/с, начальная фаза φ = 10°.
Уравнение гармонических колебаний дано в виде: Х = 0,2cos(2πt + π/3), м. Найти, какую долю составляет кинетическая энергия от полной энергии в момент времени t = T/6.
Уравнение гармонических колебаний тела имеет вид x = 0,1sin π(t/8+1/4), м. Чему равны амплитуда, частота и начальная фаза колебаний?
Уравнение гармонических колебаний тела имеет вид x = 0,01sin π(t/8+1/2), м. Чему равны амплитуда, частота и начальная фаза колебаний?
Уравнение гармонических колебаний тела имеет вид x = cos 5πt, см. Определите амплитуду, циклическую частоту, период и начальную фазу этих колебаний.
Уравнение гармонических колебаний тела имеет вид x = 4sin π(t+0,1), см. Определите амплитуду, циклическую частоту, период и начальную фазу.
Уравнение гармонических колебаний тела имеет вид x = 5sin π(t+0,1), см. Чему равны период и циклическая частота этих колебаний?
Математический маятник длиной 80 см в начальный момент имеет максимальную скорость, равную 28 см/с. Определить уравнение гармонических колебаний маятника. Записать дифференциальные уравнения колебаний для линейного и углового смещений. Дать связь между ними.
Максимальное значение скорости гармонически колеблющейся материальной точки равно 20 см/с. Величина максимального ускорения равна 4,0 м/с 2 . Определить круговую частоту и амплитуду колебаний. Записать уравнение гармонических колебаний в общем виде, получить из него закон колебаний скорости и ускорения.
Уравнение гармонических колебаний имеет вид х = Acos(ωt). Известно, что при фазе π/6 рад смешение равно 2 см. Определить смешение и скорость точки при фазе 3π/4 рад, если период колебаний Т = 2 с.
Видео:Уравнения и графики механических гармонических колебаний. Практ. часть - решение задачи. 11 класс.Скачать
Материальная точка совершает гармонические колебания согласно уравнению х = A sin wt. Определите минимальное время от
Видео:Урок 327. Гармонические колебанияСкачать
Ваш ответ
Видео:Уравнения и графики механических гармонических колебаний. 11 класс.Скачать
решение вопроса
Видео:МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ период колебаний частота колебанийСкачать
Похожие вопросы
- Все категории
- экономические 43,299
- гуманитарные 33,630
- юридические 17,900
- школьный раздел 607,256
- разное 16,836
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Видео:Выполнялка 53.Гармонические колебания.Скачать
17. Механика 
Читать 0 мин.
Читать 0 мин.Видео:Гармонические колебания | Физика 9 класс #25 | ИнфоурокСкачать
17.547. Механические колебания
Колебания ― это процесс, при котором состояние системы изменяется, повторяясь во времени, и смещаясь то в одну, то в другую сторону относительно состояния равновесия.
Период ― это время, через которое повторяются показатели системы, т. е. система совершает одно полное колебание. Период изменяется в секундах.
Частота ― величина обратная периоду: число полных колебаний за единицу времени. Частота измеряется в герцах [Гц] = [c-1]. Частота равна v = $frac$ , где
Если известно, что тело совершает N колебаний за время t, то частоту его колебаний можно определить как v = $frac$ , где
N ― количество колебаний;
Для описания колебательных систем, совершающих круговые процессы, удобно использовать круговую (циклическую) частоту. Циклическая частота показывает количество полных колебаний, которые происходят за 2π секунд и равна ω = 2πvили ω = $frac$ , где
ω ― циклическая частота [рад/с];
Гармонические колебания ― колебания, в которых физические величины изменяются по закону синуса или косинуса. Кинематическое уравнение гармонических колебаний имеет вид:
ω ― циклическая частота [рад/с];
φ0 ― начальная фаза колебаний, [рад];
Смещение (x) ― это отклонение тела от положения равновесия. Смещение также является координатой тела, если отсчитывать ее от положения равновесия.
Амплитуда колебаний (A) ― максимальное отклонение колеблющейся величины от положения равновесия, т. е. максимальное смещение равно амплитуде колебаний xmax = A.
Начальная фаза колебаний (φ0) определяет смещение в начальный момент времени, выраженное в радианах.
Фаза колебаний (φ) или полная фаза колебаний, определяет смещение в данный момент времени, выраженное в радианах. Фаза колебаний равна φ = ωt + φ0, где
φ ― полная фаза колебаний [рад];
φ0 ― начальная фаза колебаний, [рад];
ω ― циклическая частота [рад/с];
Пример анализа гармонических колебаний точки
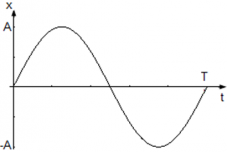
Рассмотрим гармонические колебания, в которых уравнение движения точки имеет вид x(t) = Asin(ωt), где
ω ― циклическая частота [рад/с].
Из уравнения x(t) = Asin(ωt) следует, что начального смещения нет (φ0 = 0) и колебания начинаются из положения равновесия. Смещение x достигает максимального значения xmax и равно амплитуде xmax = A, в тот момент, когда модуль синуса равен единице |sin(ωt)| = 1. Когда x = A фаза колебаний равна φ = $frac +2pi n$ когда x = –A фаза колебаний принимает значения φ = $frac +2pi n$ , где n = 0, 1 , 2, … N.
График колебания координаты точки имеет вид:
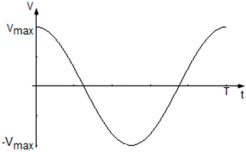
Определим уравнение и график колебания скорости. Скорость ― это производная координаты по времени: v = xt‘, где
v ― скорость движения точки [м/с];
Так как закон изменения координаты нам известен x(t) = Asin(ωt), скорость движения колеблющейся точки: v = xt‘ = |Asin(ωt)|’t = Acos(ωt).
Уравнение скорости точки равно v(t) = Acos(ωt), где
v ― скорость движения точки [м/с];
ω ― циклическая частота [рад/с];
Сравнив уравнение v(t) = Aωcos(ωt) с кинематическим уравнением гармонических колебаний, легко заметить, что Aω ― амплитуда изменения скорости, а ωt ― фаза колебаний скорости. Таким образом, максимальное значение скорости равно vmax = Aω, и оно достигается при | cos(ωt) | = 1, т. е. тогда, когда фаза колебаний скорости равна φ = πn, где n = 0, 1, 2, … N.
График колебания скорости точки имеет вид:
Аналогично определяются уравнение и график колебания ускорения точки, которая движется по гармоническому закону.
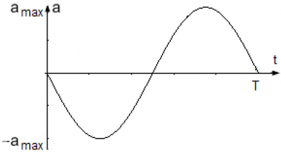
Ускорение ― это производная скорости по времени: a = vt‘, где
a ― ускорение движения точки [м/с2];
v ― скорость движения точки [м/с];
Так как закон изменения скорости был определен выше v(t) = Aωcos(ωt), определим ускорения движения колеблющейся точки: a = vt‘ = [Aωcos(ωt)]t‘ = –Aω2sin(ωt).
Уравнение ускорения точки равно a(t) = –Aω2sin(ωt), где
a ― ускорение движения точки [м/с2];
ω ― циклическая частота [рад/с];
Модуль ускорения точки максимален, когда |sin(ωt)| = 1 ― тогда же, когда достигает максимума смещение точки. Максимальное ускорение, т. е. амплитуда ускорения точки равна amax = Aω2.
График колебания ускорения точки имеет вид:
Во время гармонических колебаний, формы энергии колебательной системы все время находятся в процессе взаимной трансформации. В механической колебательной системе преобразуется механическая энергия: потенциальная энергия ― в кинетическую, а затем кинетическая энергия ― вновь в потенциальную. Полная механическая энергия колеблющейся системы постоянна, и в любой момент времени справедлив закон сохранения энергии E = EП + EK, где
E ― полная механическая энергия системы, E = const, [Дж];
EП ― потенциальная энергия системы, изменяющаяся во времени, [Дж];
EK ― кинетическая энергия системы, изменяющаяся во времени, [Дж].
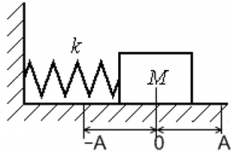
Рассмотрим изменение потенциальной энергии пружинного маятника, который колеблется по гармоническому уравнению x(t) = Asin(ωt).
Потенциальная энергия деформированной пружины равна EП = $frac$ , где
EП ― потенциальная энергия деформированной пружины, [Дж];
k ― коэффициент упругости пружины [Н/м];
x ― деформация пружины (величина ее удлинения или сжатия) [м].
У пружинного маятника деформация пружины ― переменная величина, которая зависит от времени. Кинематическое уравнение движения точки, принадлежащей этому маятнику ― x(t) = Asin(ωt). Следовательно, потенциальную энергию пружинного маятника можно записать как EП = $frac$ = $frac$ = $frac cdot A^2 sin^2 (omega t)$ .
Уравнение потенциальной энергии пружинного маятника EП = $frac cdot A^2 sin^2 (omega t)$ , где
EП ― потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
ω ― циклическая частота [рад/с];
Амплитуда потенциальной энергии пружинного маятника равна EПmax = $fracA^2$ , где
EПmax ― максимальная потенциальная энергия пружинного маятника, [Дж];
k ― коэффициент упругости пружины [Н/м];
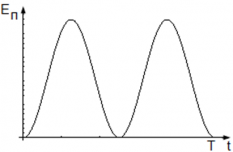
Потенциальная энергия пружинного маятника равна нулю, когда sin(ωt) = 0 ― когда маятник проходит положение равновесия, и максимальна, когда sin(ωt) = 1 ― когда маятник находится в крайних положениях, т. е. когда его смещение равно амплитуде.
График колебаний потенциальной энергии пружинного маятника:
Рассмотрим изменение кинетической энергии маятника. Кинетическая энергия тела равна Eк = $frac$ , где
Eк ― кинетическая энергия тела, [Дж];
v ― скорость движения тела, [м/с].
У тела, которое совершает колебательные движения, скорость ― переменная величина.
Выше было показано, что если уравнение движения точки имеет вид x(t) = Asin(ωt), то уравнение скорости точки v(t) = Aωcos(ωt). Таким образом, кинетическая энергия маятника равна Eк = $frac$ = $frac cdot (Aomegacos(omega t))^2$ = $frac cdot A^2 omega^2 cos^2 (omega t)$ .
Уравнение кинетической энергии маятника Eк = $frac cdot A^2 omega^2 cos^2 (omega t)$ , где
Eк ― кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с];
Амплитуда кинетической энергии маятника равна EКmax = $frac cdot A^2 omega^2$ , где
EКmax ― максимальная кинетическая энергия маятника, [Дж];
ω ― циклическая частота [рад/с].
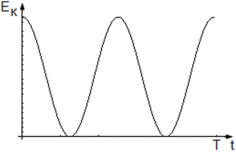
Максимальная кинетическая энергия маятника достигается тогда, когда cos2(ωt) = 1 ― маятник проходит положение равновесия, и она равна нулю, когда маятник находится в крайнем положении.
График колебаний кинетической энергии маятника:
Математический маятник ― это колебательная система, состоящая из материальной точки, подвешенной на нерастяжимой нити или стержне.
Период колебаний математического маятника равен T = $2pi sqrt<frac>$ , где
l ― длина нити математического маятника [м];
g ― ускорение свободного падения [м/с2].
Период колебаний пружинного маятника равен T = $2pi sqrt<frac>$ , где
Существует особый тип колебаний ― вынужденные колебания. Вынужденные колебания происходят только под постоянным периодическим внешним воздействием и их характеристики зависят от характеристик этого воздействия.
Если частота внешнего воздействия, которое вызывает вынужденные колебания, совпадает с собственной внутренней частотой колебательной системы ― возникает явление резонанса. При резонансе резко возрастает амплитуда колебаний системы. Частота, при которой возникает явление резонанса, называется резонансной частотой.
На рисунке показан график резонансной кривой ― увеличение амплитуды при совпадении частоты внешнего воздействия с внутренней частотой системы.
🎥 Видео
Физика. 11 класс. Уравнение и графика гармонических колебаний /03.09.2020/Скачать
5.4 Уравнение гармонических колебанийСкачать
Урок 335. Анализ графика гармонических колебанийСкачать
Тема 1. Колебательное движение. Гармонические колебания. Уравнение гармонических колебанийСкачать
График гармонического колебания | Алгебра 10 класс #23 | ИнфоурокСкачать
10 класс, 19 урок, График гармонического колебанияСкачать
Физика 9 класс (Урок№11 - Гармонические колебания. Затухающие колебания. Резонанс.)Скачать
Консультация к устному экзамену. Механика. Часть 6: "Колебания"Скачать
КОЛЕБАНИЯ физика 9 класс решение задачСкачать
Урок 325. Колебательное движение и его характеристикиСкачать
Урок 330. Скорость и ускорение при гармонических колебанияхСкачать
Как решить уравнение колебаний? | Олимпиадная физика, механические гармонические колебания, 11 классСкачать
Урок 329. Задачи на гармонические колебания - 1Скачать
Гармонические колебанияСкачать
