Уравнение Фрейндлиха для адсорбции газа имеет вид:

K и 1/n –постоянные уравнения Фрейндлиха.
Чаще всего это уравнение применяется в логарифмической форме:

Уравнение в такой форме позволяет построить линейную зависимость lnA от lnp и графически определить оба постоянных параметра.
Логарифмическое уравнение Фрейндлиха для адсорбции из раствора имеет вид:

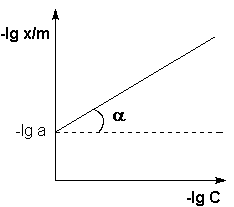
Графически определяем постоянные параметры по линейной зависимости lnA от lnC.(рис.2)
Отрезок, отсекаемый на оси ординат равен lg k, а тангенс угла наклона прямой
 |
Рис.2. Изотерма адсорбции в координатах логарифмического уравнения.
Уравнение Никольского.
При ионообменной адсорбции происходит стехиометрический обратимый обмен ионов между объемом раствора электролитов и адсорбентом.
Процессы ионного обмена на твердой поверхности характеризуются уравнением Б.П.Никольского:

где 




Графически уравнение Б.П.Никольского изображается прямой, тангенс угла наклона которой и представляют величину константы К.
Примеры решения задач:
1. Рассчитать удельную поверхность адсорбента по изотерме адсорбции бензола на его поверхности. Площадь, занимаемая молекулой бензола, S0=49·10 -20 м 2 .
| p P/PS | 0.024 | 0.08 | 0.14 | 0.20 | 0.27 | 0.35 | 0.46 |
| a·10 3 , моль/кг | 14,9 | 34,8 | 47,2 | 56,8 | 66,3 | 79.3 | 101.0 |
Решение. Проверяют применимость к экспериментальным данным теории БЭТ. С этой целью рассчитывают абсциссу и ординату уравнения изотермы адсорбции БЭТ в линейной форме, т.е.

Результаты вычислений сводят в таблицу 1 и строят график зависимости y=f(x)
| p/ps | y, кг/моль | p/ps | y, кг/моль |
| 0,024 | 1,650 | 0,27 | 5,466 |
| 0,08 | 2,499 | 0,35 | 6,790 |
| 0,14 | 3,449 | 0,46 | 8,343 |
Рис.1 изотерма адсорбции в координатах линейной формы уравнения БЭТ.
Для определения адсорбционной емкости монослоя аm по графику зависимости у=f(x) находят константы уравнения прямой линии: отрезок, отсекаемый на оси ординат при p/ps=0, b0=1.24 кг/моль, и угловой коэффициент прямой b1=15.8 кг/моль. Для сравнения вычисляют b0 и b1
методом наименьших квадратов. Данные для расчёта b0 и b1 приведены в таблице 2.
| n | x | y, кг/моль | xy, кг/моль | x 2 |
| 0,024 | 1,650 | 0,0396 | 5,76·10 -4 | |
| 0,080 | 2,499 | 0,2000 | 6,4·10 -3 | |
| 0,140 | 3,499 | 0,4830 | 1,96·10 -2 | |
| 0,200 | 4,400 | 0,8800 | 4,00·10 -2 | |
| 0,270 | 5,466 | 1,4550 | 7,08·10 -2 | |
| 0,350 | 6,790 | 2,3765 | 0,123 | |
| 0,460 | 8,434 | 3,8778 | 0,212 |
k=13,65 и am=0,0489 моль/кг.
По величине аm рассчитывают удельную поверхность адсорбента:
2. Вычислить предельный адсорбционный объём активированного угля БАУ по изотерме адсорбции бензола (таблица 3). Молярный объём бензола vm=89·10 -6 м 3 /моль.
| p/ps | a, моль/кг | p/ps | a, моль/кг | p/ps | a, моль/кг |
| 1,33·10 -6 | 0,50 | 1,63·10 -2 | 2,25 | 0,327 | 2,86 |
| 2,13·10 -5 | 0,85 | 3,77·10 -2 | 2,39 | 0,460 | 3,00 |
| 1,21·10 -4 | 1,18 | 9,47·10 -2 | 2,56 | 0,657 | 3,19 |
| 5,60·10 -4 | 1,55 | 0,201 | 2,74 | 0,847 | 4,47 |
Решение. Проверяют применимость уравнения (II.15) к экспериментальным данным. С этой целью вычисляют lg a и 

 | lg a |  | lg a |  | lg a |
| 34,52 | -0,3010 | 3,19 | 0,3522 | 0,230 | 0,4564 |
| 21,82 | -0,0706 | 2,03 | 0,3784 | 0,113 | 0,4771 |
| 15,34 | 0,0719 | 1,05 | 0,4082 | 0,033 | 0,5038 |
| 10,58 | 0,1903 | 0,48 | 0,4378 | 0,005 | 0,6503 |
Рис.2 Изотерма адсорбции в координатах линейной формы уравнения М.М.Дубинина.
Как видно из рис.2, экспериментальные точки с хорошим приближением укладываются на прямую линию и, следовательно, уравнение (15) применимо к адсорбции бензола на активированном угле БАУ.
По отрезку, отсекаемому па оси lg a при 

3. По экспериментальным данным сорбции паров воды на активированном угле при Т = 293 К построить кривую капиллярной конденсации. Показать наличие гистерезиса и, используя ветвь десорбции, построить интегральную и дифференциальную кривые распределения пор по радиусам.
аадс ·10 3 ,моль/кг. 3,75 5,3 6;2 8,75 10,4 12, 5 13 ,4
адес·10 3 , моль/кг . . .. 3,75 7,0 7,9 10,0 11,5 13,0 13,4
Vm=18·10 -3 м3/моль, σ= 72,5-10 -3 Дж/м 2 .’
Решение. Строят изотерму капиллярной конденсации в соответствии с условием задачи. Выбирают ряд точек на ветви десорбции (не менее шести—восьми), соответствующих определенным значениям p/pS, и рассчитывают объем пор, заполненных конденсатом, по уравнению V=aVm. Затем для этих же значений по уравнению
рассчитывают максимальный радиус пор, заполненных конденсатом при соответствующих давлениях p/ps. Полученные данные записывают в табл. 5 и строят структурную кривую адсорбента в координатах V=f(r). Из кривой находят ряд значений ΔV/Δr (табл.6) и строят дифференциальную кривую распределения объёма пор по радиусам в координатах ΔV/Δr=f(r)
Таблица.5 Данные для построения интегральной кривой распределения объёма пор по радиусам.
| № точки | P/PS | aдес·10 3 ,моль/кг | V·10 6 ,м 3 /кг | r·10 10 ,м |
| 0,05 0,1 0,2 0,4 0,6 0,8 0,9 0,98 | 0,5 3,7 7,0 7,9 9,0 10,0 10,9 11,5 | 0,9 66,6 126,0 142,0 162,0 180,0 196,0 207,0 | 2,2 4,6 6,6 8,5 11,6 15,5 20,2 26,3 |
Таблица.6 Данные для построения дифференциальной кривой распределения объёма по радиусам.
| ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м | ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м | ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м |
| 1,5 0,5 |
Рис.3 Интегральная(1) и дифференциальная(2) кривые распределения.
Задачи
1. Ниже приведены экспериментальные данные по адсорбции азота на TiO2 (рутиле) при 75 К:
P·10 2 Па……….60,94 116,41 169,84 218,65 275,25
А, моль/кг……. 0,367 0,417 0,467 0,512 0,567
Постройте график соответствующий линейному уравнению БЭТ. Найдите константы 
занимаемая одной молекулой азота S0=0,16 нм 2 .
2.Окись углерода адсорбируется на слюде; данные при 90 К представлены ниже. Определите, какой изотерме – Лэнгмюра или Фрейндлиха – лучше соответствуют эти данные? Каково значение К для адсорбционного равновесия? Взяв общую поверхность равной 6200см 2 , рассчитайте площадь, занимаемую каждой адсорбированной молекулой.
Vа, см 3 ……………..0,130 0,150 0,162 0,166 0,175 0,180
Р, мм. рт. cт.………. 100 200 300 400 500 600.
3.При измерении адсорбции газообразного азота на активном угле при 194.4К были получены следующие данные:
р·10 -3 , Па……………….1,86 6,12 17,96 33,65 68,89
А·10 3 , м 3 /кг…………..…5,06 14,27 23,61 32,56 40,83
Значения А даны для азота при нормальных условиях.
Рассчитайте, постоянные в уравнение Лэнгмюра и удельную поверхность активированного угля, принимая плотность газообразного азота равной
1,25 кг/м 3 , а площадь занимаемую одной молекулой азота на поверхности адсорбента, равной 0,16 нм 2 .
4.При измерении адсорбции азота на активированном угле при 273 К были получены следующие данные:
А,см 3 /г…………..……0,987 3,04 5,08 7,04 10,31
Р, мм. рт. ст…….……3,93 12,98 22,94 34,01 56,23
Построить график в координатах, в которых происходит спрямление уравнения изотермы Лэнгмюра, и определить константы этого уравнения.
5.Определите константы эмпирического уравнения Фрейндлиха, используя следующие данные об адсорбции диоксида углерода на активном угле при 293 К:
Р·10 -3 , Па…………1,00 4,48 10,0 14,4 25,0 45,2
А·10 2 , кг/кг……….3,23 6,67 9,62 11,72 14,5 17,7.
6.Используя уравнение БЭТ, построить изотерму адсорбции бензола по нижеуказанным данным и рассчитайте удельную поверхность адсорбента по изотерме адсорбции бензола (варианты 1-4):
1. P/Ps.………..0,04 0,08 0,16 0,22 0,27 0,36 0,46
А, моль/кг……. 0,348 0,483 0,624 0,724 0,805 0,928 0,13
2. Р/Рs………. 0,05 0,12 0,19 0,26 0,34 0,44 0,50
А, моль/кг ……. 0,31 0,593 0,795 0,99 1,21 1,525 1,77
3. Р/Рs……….…0,03 0,07 0,12 0,17 0,24 0,31 0,38
А, моль/кг……. 0,196 0,301 0,373 0,423 0,488 0,52 0,625
4. Р/Рs…………. 0,02 0,05 0,11 0,19 0,25 0,3 0,36
А, моль/кг……. 0,104 0,196 0,298 0,387 0,443 0,488 0,55
Площадь, занимаемую молекулой бензола, примите равной 0,49 нм 2 .
7.Используя уравнение БЭТ, рассчитайте удельную поверхность адсорбента по данным об адсорбции азота:
А•10 3 , м 3 /кг…………..0,71 0,31 0,93 1,09
Площадь занимаемая молекулой азота в плотном монослое, равна 0,16 нм 2 ,
Плотность азота 1,25 кг/м 3 .
8.При обработке данных по адсорбции азота на графитированной саже при 77 К с помощью графика, соответствующего линейному уравнению БЭТ,
найдено, что тангенс угла наклона прямой составляет 1,5•10 3 , а отрезок, отсекаемый на оси ординат, равен 5 единицам (адсорбция выражена в м 3 азота на 1 кг адсорбента при нормальных условиях). Рассчитайте удельную поверхность адсорбента, предполагая, что площадь, занимаемая одной молекулой азота, равна 0,16 нм 2 .
9.Ниже приведены результаты измерения адсорбции газообразного криптона (при 77,5К) на катализаторе:
А·10 3 , м 3 /кг…………1,27 1,5 1,76 1,9 1,98
Р, Па……………..…13,22 23,99 49,13 75,70 91,22.
Значения А для криптона даны при нормальных условиях. Определите константы уравнения БЭТ и удельную поверхность катализатора, принимая, что один атом криптона занимает площадь 0,195нм 2 , Рs=342,6 Па, плотность криптона равна 3,74 кг/м 3
10.используя уравнение БЭТ, рассчитайте удельную поверхность адсорбента по изотерме адсорбции азота:
А, моль/кг……..2,16 2,39 2,86 3,02 3,22 3,33
Площадь занимаемая одной молекулой азота в адсорбционном слое 0,16 нм 2 .
11.По изотерме адсорбции азота определить удельную поверхность адсорбента
(Т=77 К, S0=16,2·10 -20 м 2 ). (Варианты 1-5).
1. Р/Рs………. 0,04 0,09 0,16 0,20 0,30
А, моль/кг… .2,20 2,62 2,94 3,11 3,58
2. Р/Рs…………0,029 0,05 0,11 0,14 0,20
А, моль/кг………..2,16 2,39 2,86 3,02 3,33
3. Р/Рs………….0,02 0,04 0,08 0,14 0,16 0,18
А, моль/кг………..1,86 2,31 2,72 3,07 3,12 3,23
Для следующих двух вариантов объем адсорбированного газа приведен к нормальным условиям:
4. Р/Рs…………….…0,05 0,10 0,15 0,20 0,25 0,30
А·10 2 м 3 /кг……………..0,70 1,10 1,17 1,32 1,45 1,55
5. Р/Рs……………….0,029 0,05 0,11 0,14 0,18 0,20
А·10 2 м 3 /кг……..……..0,48 0,54 0,64 0,68 0,72 0,75
12.По изотерме адсорбции бензола определить удельную поверхность
адсорбента. Т=293 К, S0=49•10 -20 м 2 . Объем адсорбированного газа приведен к нормальным условиям (варианты 1-4):
1. Р/Рs…………………….0,05 0,10 0,15 0,20 0,25 0,30
А·10 2 , м 3 /кг………………..0,86 1,20 1,40 1,60 1,80 1,90
2. Р/Рs…………………….0,10 0,15 0,20 0,25 0,30 0,35
А·10 2 , м 3 /кг……….………..1,15 1,37 1,55 1,71 1,86 1,99
3. Р/Рs…………………….0,10 0,15 0,20 0,25 0,30 0,35
А·10 2 , м 3 /кг………………..0,89 1,09 1,27 1,45 1,60 1,78
4. Р/Рs…………………….0,08 0,16 0,25 0,35 0,45 0,52
А·10 2 , м 3 /кг………..… ……1,03 1,37 1,70 1,99 2,44 2,82
13.По изотерме адсорбции бензола определить удельную поверхность
адсорбента. Т=293 К, S0=49·10 -20 м 2 (варианты 1-3).
1. Р/Рs……………..0,05 0,10 0,15 0,20 0,30 0,40
А, моль/кг…. ………0,36 0,51 0,60 0,68 0,82 0,98
2. Р/Рs…………. ….0,06 0,12 0,20 0,30 0,40 0,50
А, моль/кг…. ………..0,08 0,16 0,25 0,35 0,45 0,52
3. Р/Рs…………. ….0,46 0,61 0,76 0,89 1,09 1,26
14.Построить изотерму адсорбции нитролигнина на глине и определить константы уравнения Фрейндлиха по следующим экспериментальным данным:
Концентрация водного раствора нитролигнина
Г·10 3 , кг/кг……………………5,0 12,0 21,0 26,0 35,0 38,0.
15.Пользуясь экспериментальными данными ионного обмена ионов кальция (Г1с1) и натрия (Г2с2) на синтетическом катионите, определить графически константу уравнения Никольского К:



16.Пользуясь константами уравнения Фрейндлиха k=4,17·10 -3 , 1/n=0,4, рассчитать и построить изотерму адсорбции углекислого газа на угле для следующих интервалов давления: 100·10 2 , 200·10 2 , 400·10 2 , 500·10 2 Н/м 2 .
17. Пользуясь константами уравнения Фрейндлиха k=3,2·10 -3 , 1/n=0,6 построить кривую адсорбции углекислого газа на угле в интервале давлений от 5·10 2 до 25·10 2 Н/м 2 .
18. По данным сорбции углекислого газа на угле построить изотерму адсорбции и определить константы изотермы адсорбции Фрейндлиха:
Р·10 -2 , Н/м 2 ……………..5,0 10,0 30,0 50,0 75,0 100,0
Г·10 3 , кг/кг……………..30, 5,5 16,0 23,0 31,0 35,0.
19. При изучении реакций обмена Mg-ионов из чернозема с ионами Ca из внесенных минеральных удобрений получены следующие результаты:
Концентрация ионов в растворе Количество сорбированных катионов
С·10 3 , кмоль/м 3 Г·10 5 ,кмоль/кг
2,41 4,75 8,12 42,88
2,25 5,00 7,70 43,30
2,00 5,10 6,90 44,10
1,84 5,50 6,10 44,90
1,53 5,87 4,54 46,46
1,37 5,99 4,12 46,88
Графическим методом определить константу уравнения Никольского.
20.Оределить константу уравнения Никольского К, используя экспериментальные данные реакций обмена ионов Ca из почвы на ионы Na из раствора натриевой соли.
Концентрация ионов в растворе Na…3,26 6,60 13,80 21,25 38,41 65,19
С·10 3 , кмоль/м 3 Ca.…37,84 36,72 34,62 31,87 26,16 17,10
Количество сорбированных Na….0,28 0,60 1,20 1,89 3,18 7,62
ионов Г·10 5 , кмоль/кг Ca…39,72 39,56 39,40 38,93 38,68 37,40
21.Пользуясь экспериментальными данными реакций обмена ионов ионов Na из раствора натриевой соли на ионы Mg из почвы, определить графически константу уравнения Никольского:
Концентрация ионов в растворе Количество сорбированных ионов
С·10 3 ,кмоль/м 3 на почве Г.10 5 , кмоль/кг
13,82 41,92 1,16 25,40
21,25 38,30 1,89 26,13
38,19 31,90 3,62 27,20
65,0 21,14 8,01 29,32
79,25 14,73 11,66 32,84
22. Используя экспериментальные данные адсорбции анилина из его водного раствора на угле, определить графически константы уравнения Лэнгмюра и построить изотерму адсорбции для следующих с1:
C1·10 4 , кмоль/м 3 ……………………3 5 10 15 20
анилина с·10 4 , кмоль/ м …………1,0 4,0 7,5 12,5 17,5
А·10 9 ,кмоль/м 2 …………….……0,3 0,58 0,70 0,87 0,92
23.По экспериментальным данным построить кривую адсорбции углекислого газа на цеолите при 293º и с помощью графического метода определить константы уравнения Лэнгмюра:
Р·10 -2 , н/м 2 ……………….1,0 5,0 10,0 30,0 75,0 100,0 200,0
А·10 3 , кг/кг………………35,0 86,0 112,0 152,0 174,0 178,0 188,0
24.Используя уравнение Лэнгмюра, вычислить величину адсорбции азота на цеолите при давлении р=2,8·10 2 , если А∞=38,9·10 -3 кг/кг, а k=0,156·10 -2 .
25. Найти площадь, приходящуюся на одну молекулу в насыщенном адсорбционном слое анилина на поверхности его водного раствора, если предельная адсорбция А∞=6,0·10 -9 кмоль/м
26.По экспериментальны данным адсорбции углекислого газа на активированном угле, найти константы уравнения Лэнгмюра, пользуясь которыми рассчитать и построить изотерму адсорбции:
P·10 -2 , Н/м2……………..9,9 49,7 99,8 200,0 297,0 398,5
Г·10 3 , кг/кг……………..32,0 70,0 91,0 102,0 107,3 108,0.
27.По константам уравнения Лэнгмюра А∞=182·10 -3 и k=0,1·10 -2 рассчитать и построить изотерму адсорбции углекислого газа на активированном угле в пределах следующих равновесных давлений газа: 10·10 2 – 400·10 2 Н/м.
28.Построить кривую адсорбции углекислого газа на активированном угле при 231 º и определить константы эмпирического уравнения Фрейндлиха, пользуясь следующими экспериментальными данными:
Р·10 -2 , Н/м 2 ………………10,0 44,8 100,0 144,0 250,0 452,0
А·10 3 , кг/кг……………….32,3 66,7 96,2 117,2 145,0 177,0.
29. Используя константы эмпирического уравнения Фрейндлиха k=1,6·10 -3 и 1/n=0,48, построить кривую адсорбции углекислого газа на активированном угле при 271 º в интервале давлений от 2·10 2 до 30·10 2 Н/м 2 .
30. Определить постоянные эмпирического уравнения Фрейндлиха, используя следующие данные для адсорбции при 231К углекислого газа на угле из коксовой скорлупы:
Р, Па·10 -3 ……………….1,000 4,480 10,000 14,40 25,0 45,2
А, кг/кг·10 2 ………………3,23 6,67 9,62 11,72 14,5 17,7.
31. Вычислите площадь поверхности катализатора, если для образования монослоя на нем должно адсорбироваться 103 см 3 /г азота (объем приведен к 760 мм рт.ст. и 0ºС). Адсорбция измеряется при температуре 195ºС. Эффективная площадь, занимаемая молекулой азота при этой температуре, равна 16,2 А 2 .
32.Площадь поверхности 1 г активированного угля равна 1000 м 2 . Какое количество аммиака может адсорбироваться на поверхности 45 г угля при 45ºС и 1 атм, если принять в качестве предельного случая полное покрытие поверхности? Диаметр молекулы аммиака равен 3·10 -10 м. Принимается, что молекулы касаются друг друга так, что центры четырех соседних сфер расположены в углах квадрата.
33. Ниже представлены данные по хемосорбции водорода на порошке меди при 25ºС. Подтвердите, что они подчиняются изотерме Ленгмюра. Затем найдите значение К для адсорбционного равновесия и адсорбционный объем, соответствующий полному покрытию.
Р, мм рт ст…………………..0,19 0,97 1,90 4,05 7,5 11,95
Vа, см 3 ……………………….0,042 0,163 0,221 0,321 0,411 0,471.
34. Определите, какая изотерма – Лэнгмюра или Фрейндлиха – лучше соответствует данным для адсорбции метана на 10 г сажи при 0ºС, приведенным ниже:
Видео:Линейные диофантовы уравненияСкачать

Уравнение фрейндлиха в линейной форме
Теоретические представления, развитые Ленгмюром и Поляни, в значительной степени идеализируют и упрощают истинную картину адсорбции. На самом деле поверхность адсорбента неоднородна, между адсорбированными частицами имеет место взаимодействие, активные центры не являются полностью независимыми друг от друга и т.д. Все это усложняет вид уравнения изотермы. Г. Фрейндлих показал, что при постоянной температуре число молей адсорбированного газа или растворенного вещества, приходящееся на единицу массы адсорбента (т.н. удельная адсорбция x/m), пропорционально равновесному давлению (для газа) или равновесной концентрации (для веществ, адсорбируемых из раствора) адсорбента, возведенным в некоторую степень, которая всегда меньше единицы:
Изотерма адсорбции Фрейндлиха в обычных (а) и логарифмических (б)
координатах
Показатель степени n и коэффициент пропорциональности а в уравнении Фрейндлиха определяются экспериментально. Логарифмируя уравнения, получаем:
Т.о., зависимость логарифма удельной адсорбции от логарифма концентрации (давления) графически выражается прямой линией, отсекающей на оси ординат отрезок, равный lga, тангенс угла наклона которой к оси абсцисс равен по величине показателю степени при давлении или концентрации:
Видео:5.1. Адсорбция. Классификация адсорбцииСкачать

Уравнение Фрейндлиха
Теоретические представления, развитые Лэнгмюром и Поляни, в значительной степени идеализируют и упрощают истинную картину адсорбции. На самом деле поверхность адсорбента неоднородна, между адсорбированными частицами имеет место взаимодействие, активные центры не являются полностью независимыми друг от друга и т.д. Все это усложняет вид уравнения изотермы. Г.Фрейндлих предположил, что число молей адсорбированного газа или растворенного вещества, приходящееся на единицу массы адсорбента (т.н. удельная адсорбция x/m) должна быть пропорциональна равновесному давлению (для газа) или равновесной концентрации (для веществ, адсорбируемых из раствора) адсорбента, возведенной в некоторую степень, которая всегда меньше единицы:
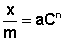
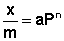
Рис. 4.7. Изотерма адсорбции Фрейндлиха в логарифмических координатах.
Показатель степени n и коэффициент пропорциональности а в уравнении Фрейндлиха определяются экспериментально. Логарифмируя уравнения (IV.15 — IV.16), получаем:
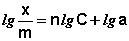
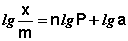
Т.о., зависимость логарифма удельной адсорбции от логарифма концентрации (давления) графически выражается прямой линией, отсекающей на оси ординат отрезок, равный lga, тангенс угла наклона которой к оси абсцисс равен по величине показателю степени при давлении или концентрации (рис. 4.7):
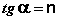
4.1.5 Адсорбция на границе твердое тело – раствор
💥 Видео
Математика. Линейные диофантовы уравнения с двумя неизвестными. Центр онлайн-обучения «Фоксфорд»Скачать

АдсорбцияСкачать

Как решать Диофантовы уравнения ★ 9x+13y=-1 ★ Решите уравнение в целых числахСкачать

Практическое занятие 4. Адсорбция на границе твердое тело – газСкачать

Уравнение ЛенгмюраСкачать

Адсорбция на твёрдой поверхностиСкачать

Полезные мелочи | алгоритм Евклида | диофантовы уравнения | примеры | 1Скачать

Уравнения Лагранжа второго рода. Задача 1Скачать

Урок 101 (осн). Связь коэффициентов линейного и объемного расширенияСкачать

Поверхностные явления: адгезия, смачивание, адсорбция | Коллоидная химияСкачать

19. Метод вариации произвольных постоянных. Линейные неоднородные диф уравнения 2-го порядкаСкачать

#86. Делимость и диофантовы уравнения! ТРУДНАЯ ЗАДАЧА!Скачать

Поверхностные явления. Адсорбция на неподвижных границах раздела фаз.Скачать

Практическое занятие 6. Адсорбция на границе раствор – газСкачать

Уравнение Эйлера - bezbotvyСкачать

Поверхностные явленияСкачать

Ягола А. Г. - Вариационное исчисление - Метод регуляризации ТихоноваСкачать