План лекции:
1.Поверхностное натяжение — физический смысл.
Видео:Уравнение ЛенгмюраСкачать

АДСОРБЦИЯ
Поверхностная энергия стремится самопроизвольно уменьшиться. Это выражается в уменьшении межфазной поверхности или поверхностного натяжения ( s )
Вследствие этого стремления происходит адсорбция.
Адсорбция — процесс самопроизвольного перераспределения компонентов системы между поверхностным слоем и объемной фазой. Т.е. адсорбция может происходить в многокомпонентных системах, в слой переходит тот компонент, который сильнее уменьшает s .
Адсорбент — фаза определяющая форму поверхности, более плотная, может быть твердой или жидкой.
Адсорбат — вещество которое перераспределяется (газ или жидкость).
Десорбция — переход вещества из поверхностного слоя в объемную фазу.
Количественно адсорбцию описывают величиной Гиббсовской адсорбции (избыток вещества в поверхностном слое по сравнению с его количеством в объемной фазе, отнесенный к единице площади поверхности или единице массы адсорбента)

Г i -Гиббсовская адсорбция,
V -объем системы,
с0 -исходная концентрация адсорбата ,
с i — концентрация адсорбата в объеме,
S — площадь поверхности раздела.
Все величины в (3.1) могут быть установлены экспериментально.
Адсорбцию можно рассматривать как процесс превращения поверхностной энергии в химическую.
Выведем соотношение между поверхностным натяжением и химическими параметрами компонентов.
Если объем поверхностного слоя равен 0, то
т.к. внутр. энергия пропорциональна экстенсивным величинам, то:
полный дифференциал от тех же переменных запишется следующим образом:
dU=T dS + S dT + s dS +S d s + å m i dn i + å n i d m (3.3)
Подставляя dU из 3.2 в 3.3, получим:
3.4 и 3.5 — уравнения Гиббса для межфазной поверхности (поверхностного слоя).
Все экстенсивные величины поверхности зависят от площади поверхности , поэтому удобнее относить эти параметры к единице площади поверхности. Разделив уравнение 3.5 на площадь поверхности, получим:


Г i — поверхностный избыток компонента i в поверхностном слое (по сравнению с его равновесной концентрацией в объемной фазе), то есть величина Гиббсовской адсорбции.
Уравнение 3.6 — фундаментальное адсорбционное уравнение Гиббса. Это строгое термодинамическое соотношение, написанное для многокомпонентной системы. Однако, практиче ское его использование неудобно. Оно, например, не раскрывает зависимость поверхностного натяжения от адсорбции конкретного вещества при постоянных химических потенциалах других веществ.. Единицы величины гиббсовской адсорбции определяются единицами химического потенциала. Если потенциал отнесен к молю вещества, то величина адсорбции выражается в молях на единицу площади.
Адсорбция конкретного вещества при постоянных химических параметрах других веществ:
Принимая во внимание , что m i = m i o + RT ln ai, m i и m i o — равновесное и стандартное значения химического потенциала адсорбата i , а i — термодинамическая активность адсорбата, d m i = RT d ln ai ,получим :
для Гиббсовской адсорбции:

3.7. применяют только тогда, когда можно использовать концентрации вместо активностей и пренебречь изменениями концентраций других веществ при изменении концентрации одного вещества. Этим условиям удовлетворяет разбавленный раствор относительно данного компонента. В таком растворе при изменении концентрации растворенного вещества практически не изменяется концентрация растворителя. Поэтому для растворенного вещества уравнение 3.7 переходит в широко используемые адсорбционные уравнения Гиббса для неэлектролитов и электролитов


Видео:Практическое занятие 5. Уравнение БЭТ. Удельная поверхностьСкачать

УРАВНЕНИЕ ГЕНРИ, ФРЕЙНДЛИХА, ЛЕНГМЮРА
Для описания процесса адсорбции, помимо фундаментального уравнения адсорбции Гиббса, применяют ряд других аналитических уравнений, которые называются по имени их авторов.
При незначительном заполнении адсорбента адсорбатом отношение концентрации вещества в адсорбционном слое и в объеме стремится к постоянному значению, равному кГ:
Это уравнение характеризует изотерму адсорбции при малых концентрациях адсорбата (рис.3.1, участок 1) и является аналитическим выражением закона Генри. Коэффициент кГ не зависит от концентрации и представляет собой константу распределения, характеризующую распределение вещества в адсорбционном слое по отношению к его содержанию в объемной фазе. Уравнение Генри соблюдается приближенно, но это приближение достаточно для практики.
В более общем виде зависимость адсорбции от концентрации адсорбата можно определить с помощью уравнения Фрейндлиха.
Видео:5.1. Адсорбция. Классификация адсорбцииСкачать

Уравнение Фрейндлиха
Теоретические представления, развитые Лэнгмюром и Поляни, в значительной степени идеализируют и упрощают истинную картину адсорбции. На самом деле поверхность адсорбента неоднородна, между адсорбированными частицами имеет место взаимодействие, активные центры не являются полностью независимыми друг от друга и т.д. Все это усложняет вид уравнения изотермы. Г.Фрейндлих предположил, что число молей адсорбированного газа или растворенного вещества, приходящееся на единицу массы адсорбента (т.н. удельная адсорбция x/m) должна быть пропорциональна равновесному давлению (для газа) или равновесной концентрации (для веществ, адсорбируемых из раствора) адсорбента, возведенной в некоторую степень, которая всегда меньше единицы:
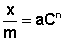
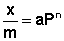
Рис. 4.7. Изотерма адсорбции Фрейндлиха в логарифмических координатах.
Показатель степени n и коэффициент пропорциональности а в уравнении Фрейндлиха определяются экспериментально. Логарифмируя уравнения (IV.15 — IV.16), получаем:
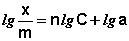
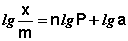
Т.о., зависимость логарифма удельной адсорбции от логарифма концентрации (давления) графически выражается прямой линией, отсекающей на оси ординат отрезок, равный lga, тангенс угла наклона которой к оси абсцисс равен по величине показателю степени при давлении или концентрации (рис. 4.7):
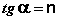
4.1.5 Адсорбция на границе твердое тело – раствор
Видео:Адсорбция на поверхностях растворовСкачать

Уравнение изотермы адсорбции Фрейндлиха
Уравнение Фрейндлиха для адсорбции газа имеет вид:

K и 1/n –постоянные уравнения Фрейндлиха.
Чаще всего это уравнение применяется в логарифмической форме:

Уравнение в такой форме позволяет построить линейную зависимость lnA от lnp и графически определить оба постоянных параметра.
Логарифмическое уравнение Фрейндлиха для адсорбции из раствора имеет вид:

Графически определяем постоянные параметры по линейной зависимости lnA от lnC.(рис.2)
Отрезок, отсекаемый на оси ординат равен lg k, а тангенс угла наклона прямой
 |
Рис.2. Изотерма адсорбции в координатах логарифмического уравнения.
Уравнение Никольского.
При ионообменной адсорбции происходит стехиометрический обратимый обмен ионов между объемом раствора электролитов и адсорбентом.
Процессы ионного обмена на твердой поверхности характеризуются уравнением Б.П.Никольского:

где 




Графически уравнение Б.П.Никольского изображается прямой, тангенс угла наклона которой и представляют величину константы К.
Примеры решения задач:
1. Рассчитать удельную поверхность адсорбента по изотерме адсорбции бензола на его поверхности. Площадь, занимаемая молекулой бензола, S0=49·10 -20 м 2 .
| p P/PS | 0.024 | 0.08 | 0.14 | 0.20 | 0.27 | 0.35 | 0.46 |
| a·10 3 , моль/кг | 14,9 | 34,8 | 47,2 | 56,8 | 66,3 | 79.3 | 101.0 |
Решение. Проверяют применимость к экспериментальным данным теории БЭТ. С этой целью рассчитывают абсциссу и ординату уравнения изотермы адсорбции БЭТ в линейной форме, т.е.

Результаты вычислений сводят в таблицу 1 и строят график зависимости y=f(x)
| p/ps | y, кг/моль | p/ps | y, кг/моль |
| 0,024 | 1,650 | 0,27 | 5,466 |
| 0,08 | 2,499 | 0,35 | 6,790 |
| 0,14 | 3,449 | 0,46 | 8,343 |
Рис.1 изотерма адсорбции в координатах линейной формы уравнения БЭТ.
Для определения адсорбционной емкости монослоя аm по графику зависимости у=f(x) находят константы уравнения прямой линии: отрезок, отсекаемый на оси ординат при p/ps=0, b0=1.24 кг/моль, и угловой коэффициент прямой b1=15.8 кг/моль. Для сравнения вычисляют b0 и b1
методом наименьших квадратов. Данные для расчёта b0 и b1 приведены в таблице 2.
| n | x | y, кг/моль | xy, кг/моль | x 2 |
| 0,024 | 1,650 | 0,0396 | 5,76·10 -4 | |
| 0,080 | 2,499 | 0,2000 | 6,4·10 -3 | |
| 0,140 | 3,499 | 0,4830 | 1,96·10 -2 | |
| 0,200 | 4,400 | 0,8800 | 4,00·10 -2 | |
| 0,270 | 5,466 | 1,4550 | 7,08·10 -2 | |
| 0,350 | 6,790 | 2,3765 | 0,123 | |
| 0,460 | 8,434 | 3,8778 | 0,212 |
k=13,65 и am=0,0489 моль/кг.
По величине аm рассчитывают удельную поверхность адсорбента:
2. Вычислить предельный адсорбционный объём активированного угля БАУ по изотерме адсорбции бензола (таблица 3). Молярный объём бензола vm=89·10 -6 м 3 /моль.
| p/ps | a, моль/кг | p/ps | a, моль/кг | p/ps | a, моль/кг |
| 1,33·10 -6 | 0,50 | 1,63·10 -2 | 2,25 | 0,327 | 2,86 |
| 2,13·10 -5 | 0,85 | 3,77·10 -2 | 2,39 | 0,460 | 3,00 |
| 1,21·10 -4 | 1,18 | 9,47·10 -2 | 2,56 | 0,657 | 3,19 |
| 5,60·10 -4 | 1,55 | 0,201 | 2,74 | 0,847 | 4,47 |
Решение. Проверяют применимость уравнения (II.15) к экспериментальным данным. С этой целью вычисляют lg a и 

 | lg a |  | lg a |  | lg a |
| 34,52 | -0,3010 | 3,19 | 0,3522 | 0,230 | 0,4564 |
| 21,82 | -0,0706 | 2,03 | 0,3784 | 0,113 | 0,4771 |
| 15,34 | 0,0719 | 1,05 | 0,4082 | 0,033 | 0,5038 |
| 10,58 | 0,1903 | 0,48 | 0,4378 | 0,005 | 0,6503 |
Рис.2 Изотерма адсорбции в координатах линейной формы уравнения М.М.Дубинина.
Как видно из рис.2, экспериментальные точки с хорошим приближением укладываются на прямую линию и, следовательно, уравнение (15) применимо к адсорбции бензола на активированном угле БАУ.
По отрезку, отсекаемому па оси lg a при 

3. По экспериментальным данным сорбции паров воды на активированном угле при Т = 293 К построить кривую капиллярной конденсации. Показать наличие гистерезиса и, используя ветвь десорбции, построить интегральную и дифференциальную кривые распределения пор по радиусам.
аадс ·10 3 ,моль/кг. 3,75 5,3 6;2 8,75 10,4 12, 5 13 ,4
адес·10 3 , моль/кг . . .. 3,75 7,0 7,9 10,0 11,5 13,0 13,4
Vm=18·10 -3 м3/моль, σ= 72,5-10 -3 Дж/м 2 .’
Решение. Строят изотерму капиллярной конденсации в соответствии с условием задачи. Выбирают ряд точек на ветви десорбции (не менее шести—восьми), соответствующих определенным значениям p/pS, и рассчитывают объем пор, заполненных конденсатом, по уравнению V=aVm. Затем для этих же значений по уравнению
рассчитывают максимальный радиус пор, заполненных конденсатом при соответствующих давлениях p/ps. Полученные данные записывают в табл. 5 и строят структурную кривую адсорбента в координатах V=f(r). Из кривой находят ряд значений ΔV/Δr (табл.6) и строят дифференциальную кривую распределения объёма пор по радиусам в координатах ΔV/Δr=f(r)
Таблица.5 Данные для построения интегральной кривой распределения объёма пор по радиусам.
| № точки | P/PS | aдес·10 3 ,моль/кг | V·10 6 ,м 3 /кг | r·10 10 ,м |
| 0,05 0,1 0,2 0,4 0,6 0,8 0,9 0,98 | 0,5 3,7 7,0 7,9 9,0 10,0 10,9 11,5 | 0,9 66,6 126,0 142,0 162,0 180,0 196,0 207,0 | 2,2 4,6 6,6 8,5 11,6 15,5 20,2 26,3 |
Таблица.6 Данные для построения дифференциальной кривой распределения объёма по радиусам.
| ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м | ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м | ΔV/Δr·10 — 4 ,м 2 /кг | Δr·10 10 ,м |
| 1,5 0,5 |
Рис.3 Интегральная(1) и дифференциальная(2) кривые распределения.
Задачи
1. Ниже приведены экспериментальные данные по адсорбции азота на TiO2 (рутиле) при 75 К:
P·10 2 Па……….60,94 116,41 169,84 218,65 275,25
А, моль/кг……. 0,367 0,417 0,467 0,512 0,567
Постройте график соответствующий линейному уравнению БЭТ. Найдите константы 
занимаемая одной молекулой азота S0=0,16 нм 2 .
2.Окись углерода адсорбируется на слюде; данные при 90 К представлены ниже. Определите, какой изотерме – Лэнгмюра или Фрейндлиха – лучше соответствуют эти данные? Каково значение К для адсорбционного равновесия? Взяв общую поверхность равной 6200см 2 , рассчитайте площадь, занимаемую каждой адсорбированной молекулой.
Vа, см 3 ……………..0,130 0,150 0,162 0,166 0,175 0,180
Р, мм. рт. cт.………. 100 200 300 400 500 600.
3.При измерении адсорбции газообразного азота на активном угле при 194.4К были получены следующие данные:
р·10 -3 , Па……………….1,86 6,12 17,96 33,65 68,89
А·10 3 , м 3 /кг…………..…5,06 14,27 23,61 32,56 40,83
Значения А даны для азота при нормальных условиях.
Рассчитайте, постоянные в уравнение Лэнгмюра и удельную поверхность активированного угля, принимая плотность газообразного азота равной
1,25 кг/м 3 , а площадь занимаемую одной молекулой азота на поверхности адсорбента, равной 0,16 нм 2 .
4.При измерении адсорбции азота на активированном угле при 273 К были получены следующие данные:
А,см 3 /г…………..……0,987 3,04 5,08 7,04 10,31
Р, мм. рт. ст…….……3,93 12,98 22,94 34,01 56,23
Построить график в координатах, в которых происходит спрямление уравнения изотермы Лэнгмюра, и определить константы этого уравнения.
5.Определите константы эмпирического уравнения Фрейндлиха, используя следующие данные об адсорбции диоксида углерода на активном угле при 293 К:
Р·10 -3 , Па…………1,00 4,48 10,0 14,4 25,0 45,2
А·10 2 , кг/кг……….3,23 6,67 9,62 11,72 14,5 17,7.
6.Используя уравнение БЭТ, построить изотерму адсорбции бензола по нижеуказанным данным и рассчитайте удельную поверхность адсорбента по изотерме адсорбции бензола (варианты 1-4):
1. P/Ps.………..0,04 0,08 0,16 0,22 0,27 0,36 0,46
А, моль/кг……. 0,348 0,483 0,624 0,724 0,805 0,928 0,13
2. Р/Рs………. 0,05 0,12 0,19 0,26 0,34 0,44 0,50
А, моль/кг ……. 0,31 0,593 0,795 0,99 1,21 1,525 1,77
3. Р/Рs……….…0,03 0,07 0,12 0,17 0,24 0,31 0,38
А, моль/кг……. 0,196 0,301 0,373 0,423 0,488 0,52 0,625
4. Р/Рs…………. 0,02 0,05 0,11 0,19 0,25 0,3 0,36
А, моль/кг……. 0,104 0,196 0,298 0,387 0,443 0,488 0,55
Площадь, занимаемую молекулой бензола, примите равной 0,49 нм 2 .
7.Используя уравнение БЭТ, рассчитайте удельную поверхность адсорбента по данным об адсорбции азота:
А•10 3 , м 3 /кг…………..0,71 0,31 0,93 1,09
Площадь занимаемая молекулой азота в плотном монослое, равна 0,16 нм 2 ,
Плотность азота 1,25 кг/м 3 .
8.При обработке данных по адсорбции азота на графитированной саже при 77 К с помощью графика, соответствующего линейному уравнению БЭТ,
найдено, что тангенс угла наклона прямой составляет 1,5•10 3 , а отрезок, отсекаемый на оси ординат, равен 5 единицам (адсорбция выражена в м 3 азота на 1 кг адсорбента при нормальных условиях). Рассчитайте удельную поверхность адсорбента, предполагая, что площадь, занимаемая одной молекулой азота, равна 0,16 нм 2 .
9.Ниже приведены результаты измерения адсорбции газообразного криптона (при 77,5К) на катализаторе:
А·10 3 , м 3 /кг…………1,27 1,5 1,76 1,9 1,98
Р, Па……………..…13,22 23,99 49,13 75,70 91,22.
Значения А для криптона даны при нормальных условиях. Определите константы уравнения БЭТ и удельную поверхность катализатора, принимая, что один атом криптона занимает площадь 0,195нм 2 , Рs=342,6 Па, плотность криптона равна 3,74 кг/м 3
10.используя уравнение БЭТ, рассчитайте удельную поверхность адсорбента по изотерме адсорбции азота:
А, моль/кг……..2,16 2,39 2,86 3,02 3,22 3,33
Площадь занимаемая одной молекулой азота в адсорбционном слое 0,16 нм 2 .
11.По изотерме адсорбции азота определить удельную поверхность адсорбента
(Т=77 К, S0=16,2·10 -20 м 2 ). (Варианты 1-5).
1. Р/Рs………. 0,04 0,09 0,16 0,20 0,30
А, моль/кг… .2,20 2,62 2,94 3,11 3,58
2. Р/Рs…………0,029 0,05 0,11 0,14 0,20
А, моль/кг………..2,16 2,39 2,86 3,02 3,33
3. Р/Рs………….0,02 0,04 0,08 0,14 0,16 0,18
А, моль/кг………..1,86 2,31 2,72 3,07 3,12 3,23
Для следующих двух вариантов объем адсорбированного газа приведен к нормальным условиям:
4. Р/Рs…………….…0,05 0,10 0,15 0,20 0,25 0,30
А·10 2 м 3 /кг……………..0,70 1,10 1,17 1,32 1,45 1,55
5. Р/Рs……………….0,029 0,05 0,11 0,14 0,18 0,20
А·10 2 м 3 /кг……..……..0,48 0,54 0,64 0,68 0,72 0,75
12.По изотерме адсорбции бензола определить удельную поверхность
адсорбента. Т=293 К, S0=49•10 -20 м 2 . Объем адсорбированного газа приведен к нормальным условиям (варианты 1-4):
1. Р/Рs…………………….0,05 0,10 0,15 0,20 0,25 0,30
А·10 2 , м 3 /кг………………..0,86 1,20 1,40 1,60 1,80 1,90
2. Р/Рs…………………….0,10 0,15 0,20 0,25 0,30 0,35
А·10 2 , м 3 /кг……….………..1,15 1,37 1,55 1,71 1,86 1,99
3. Р/Рs…………………….0,10 0,15 0,20 0,25 0,30 0,35
А·10 2 , м 3 /кг………………..0,89 1,09 1,27 1,45 1,60 1,78
4. Р/Рs…………………….0,08 0,16 0,25 0,35 0,45 0,52
А·10 2 , м 3 /кг………..… ……1,03 1,37 1,70 1,99 2,44 2,82
13.По изотерме адсорбции бензола определить удельную поверхность
адсорбента. Т=293 К, S0=49·10 -20 м 2 (варианты 1-3).
1. Р/Рs……………..0,05 0,10 0,15 0,20 0,30 0,40
А, моль/кг…. ………0,36 0,51 0,60 0,68 0,82 0,98
2. Р/Рs…………. ….0,06 0,12 0,20 0,30 0,40 0,50
А, моль/кг…. ………..0,08 0,16 0,25 0,35 0,45 0,52
3. Р/Рs…………. ….0,46 0,61 0,76 0,89 1,09 1,26
14.Построить изотерму адсорбции нитролигнина на глине и определить константы уравнения Фрейндлиха по следующим экспериментальным данным:
Концентрация водного раствора нитролигнина
Г·10 3 , кг/кг……………………5,0 12,0 21,0 26,0 35,0 38,0.
15.Пользуясь экспериментальными данными ионного обмена ионов кальция (Г1с1) и натрия (Г2с2) на синтетическом катионите, определить графически константу уравнения Никольского К:



16.Пользуясь константами уравнения Фрейндлиха k=4,17·10 -3 , 1/n=0,4, рассчитать и построить изотерму адсорбции углекислого газа на угле для следующих интервалов давления: 100·10 2 , 200·10 2 , 400·10 2 , 500·10 2 Н/м 2 .
17. Пользуясь константами уравнения Фрейндлиха k=3,2·10 -3 , 1/n=0,6 построить кривую адсорбции углекислого газа на угле в интервале давлений от 5·10 2 до 25·10 2 Н/м 2 .
18. По данным сорбции углекислого газа на угле построить изотерму адсорбции и определить константы изотермы адсорбции Фрейндлиха:
Р·10 -2 , Н/м 2 ……………..5,0 10,0 30,0 50,0 75,0 100,0
Г·10 3 , кг/кг……………..30, 5,5 16,0 23,0 31,0 35,0.
19. При изучении реакций обмена Mg-ионов из чернозема с ионами Ca из внесенных минеральных удобрений получены следующие результаты:
Концентрация ионов в растворе Количество сорбированных катионов
С·10 3 , кмоль/м 3 Г·10 5 ,кмоль/кг
2,41 4,75 8,12 42,88
2,25 5,00 7,70 43,30
2,00 5,10 6,90 44,10
1,84 5,50 6,10 44,90
1,53 5,87 4,54 46,46
1,37 5,99 4,12 46,88
Графическим методом определить константу уравнения Никольского.
20.Оределить константу уравнения Никольского К, используя экспериментальные данные реакций обмена ионов Ca из почвы на ионы Na из раствора натриевой соли.
Концентрация ионов в растворе Na…3,26 6,60 13,80 21,25 38,41 65,19
С·10 3 , кмоль/м 3 Ca.…37,84 36,72 34,62 31,87 26,16 17,10
Количество сорбированных Na….0,28 0,60 1,20 1,89 3,18 7,62
ионов Г·10 5 , кмоль/кг Ca…39,72 39,56 39,40 38,93 38,68 37,40
21.Пользуясь экспериментальными данными реакций обмена ионов ионов Na из раствора натриевой соли на ионы Mg из почвы, определить графически константу уравнения Никольского:
Концентрация ионов в растворе Количество сорбированных ионов
С·10 3 ,кмоль/м 3 на почве Г.10 5 , кмоль/кг
13,82 41,92 1,16 25,40
21,25 38,30 1,89 26,13
38,19 31,90 3,62 27,20
65,0 21,14 8,01 29,32
79,25 14,73 11,66 32,84
22. Используя экспериментальные данные адсорбции анилина из его водного раствора на угле, определить графически константы уравнения Лэнгмюра и построить изотерму адсорбции для следующих с1:
C1·10 4 , кмоль/м 3 ……………………3 5 10 15 20
анилина с·10 4 , кмоль/ м …………1,0 4,0 7,5 12,5 17,5
А·10 9 ,кмоль/м 2 …………….……0,3 0,58 0,70 0,87 0,92
23.По экспериментальным данным построить кривую адсорбции углекислого газа на цеолите при 293º и с помощью графического метода определить константы уравнения Лэнгмюра:
Р·10 -2 , н/м 2 ……………….1,0 5,0 10,0 30,0 75,0 100,0 200,0
А·10 3 , кг/кг………………35,0 86,0 112,0 152,0 174,0 178,0 188,0
24.Используя уравнение Лэнгмюра, вычислить величину адсорбции азота на цеолите при давлении р=2,8·10 2 , если А∞=38,9·10 -3 кг/кг, а k=0,156·10 -2 .
25. Найти площадь, приходящуюся на одну молекулу в насыщенном адсорбционном слое анилина на поверхности его водного раствора, если предельная адсорбция А∞=6,0·10 -9 кмоль/м
26.По экспериментальны данным адсорбции углекислого газа на активированном угле, найти константы уравнения Лэнгмюра, пользуясь которыми рассчитать и построить изотерму адсорбции:
P·10 -2 , Н/м2……………..9,9 49,7 99,8 200,0 297,0 398,5
Г·10 3 , кг/кг……………..32,0 70,0 91,0 102,0 107,3 108,0.
27.По константам уравнения Лэнгмюра А∞=182·10 -3 и k=0,1·10 -2 рассчитать и построить изотерму адсорбции углекислого газа на активированном угле в пределах следующих равновесных давлений газа: 10·10 2 – 400·10 2 Н/м.
28.Построить кривую адсорбции углекислого газа на активированном угле при 231 º и определить константы эмпирического уравнения Фрейндлиха, пользуясь следующими экспериментальными данными:
Р·10 -2 , Н/м 2 ………………10,0 44,8 100,0 144,0 250,0 452,0
А·10 3 , кг/кг……………….32,3 66,7 96,2 117,2 145,0 177,0.
29. Используя константы эмпирического уравнения Фрейндлиха k=1,6·10 -3 и 1/n=0,48, построить кривую адсорбции углекислого газа на активированном угле при 271 º в интервале давлений от 2·10 2 до 30·10 2 Н/м 2 .
30. Определить постоянные эмпирического уравнения Фрейндлиха, используя следующие данные для адсорбции при 231К углекислого газа на угле из коксовой скорлупы:
Р, Па·10 -3 ……………….1,000 4,480 10,000 14,40 25,0 45,2
А, кг/кг·10 2 ………………3,23 6,67 9,62 11,72 14,5 17,7.
31. Вычислите площадь поверхности катализатора, если для образования монослоя на нем должно адсорбироваться 103 см 3 /г азота (объем приведен к 760 мм рт.ст. и 0ºС). Адсорбция измеряется при температуре 195ºС. Эффективная площадь, занимаемая молекулой азота при этой температуре, равна 16,2 А 2 .
32.Площадь поверхности 1 г активированного угля равна 1000 м 2 . Какое количество аммиака может адсорбироваться на поверхности 45 г угля при 45ºС и 1 атм, если принять в качестве предельного случая полное покрытие поверхности? Диаметр молекулы аммиака равен 3·10 -10 м. Принимается, что молекулы касаются друг друга так, что центры четырех соседних сфер расположены в углах квадрата.
33. Ниже представлены данные по хемосорбции водорода на порошке меди при 25ºС. Подтвердите, что они подчиняются изотерме Ленгмюра. Затем найдите значение К для адсорбционного равновесия и адсорбционный объем, соответствующий полному покрытию.
Р, мм рт ст…………………..0,19 0,97 1,90 4,05 7,5 11,95
Vа, см 3 ……………………….0,042 0,163 0,221 0,321 0,411 0,471.
34. Определите, какая изотерма – Лэнгмюра или Фрейндлиха – лучше соответствует данным для адсорбции метана на 10 г сажи при 0ºС, приведенным ниже:
🔥 Видео
Практическое занятие 4. Адсорбция на границе твердое тело – газСкачать

АдсорбцияСкачать

Адсорбция на твёрдой поверхностиСкачать

5.2. Молекулярная адсорбция ПАВ на поверхности раздела раствор-воздухСкачать

5.3. Адсорбция на границе жидкость-газ. Поверхностно активные вещества ПАВСкачать

Поверхностные явленияСкачать

Коробов М. В. - Физическая химия. Часть 1 - Адсорбция на границе газ-твердое. Модель ЛенгмюраСкачать

Поверхностные явления. Адсорбция на подвижных границах раздела фаз.Скачать

Практическое занятие 6. Адсорбция на границе раствор – газСкачать

Адсорбция. Простой эксперимент дома / ХимХопСкачать

Поверхностные явления. Адсорбция на неподвижных границах раздела фаз.Скачать

Поверхностные явления. Адсорбция.Скачать

СорбцияСкачать

Поверхностные явления: адгезия, смачивание, адсорбция | Коллоидная химияСкачать

Дифференциальное уравнение Лагранжа II рода. Расчет механической системы.Скачать

Использование таблиц потенциалов и расчет ЭДС реакции. Продукты в ОВР. Ч.5-1.Скачать